六西格玛方法在车用雷达生产质量改善研究

苏 童 余建波 李艳冰

（1.同济大学 机械与能源工程学院 上海 201804；2.上海质量管理科学研究院 上海 200052）

毫米波雷达是在毫米波波段工作的雷达，通常指的是30～300GHz频带。与红外、激光和电视等光学雷达相比，毫米波雷达具有更强的穿透雾气、烟雾和灰尘的能力，并且具有全天候的特性。 毫米波雷达广泛用于军事领域，例如雷达检测、高速通信、导弹制导、卫星遥感、电子对策等。近年来，毫米波设备的水平，电路设计技术，天线技术和 其他相关技术已经发展和成熟。 毫米波雷达在汽车雷达中的应用也得到了很大的发展。

A公司是全球著名的汽车零部件供应商，有一款产品就是制作毫米波雷达。在生产过程中，产品出现质量问题，本文拟用六西格玛的方法和工具对该产品出现的质量问题进行改善，提升产品的良品率，降低报废，减少公司经济损失。

1 雷达生产流程及其现状

1.1 雷达产品的生产流程

雷达系统发射的电磁波信号被其发射路径上的物体阻挡继而会发生反射。通过捕捉反射的信号，雷达系统可以确定物体的距离、速度和角度。雷达主要由前盖、后盖、高频PCB板、低频PCB板、屏蔽盖组成，其生产流程如图1所示。

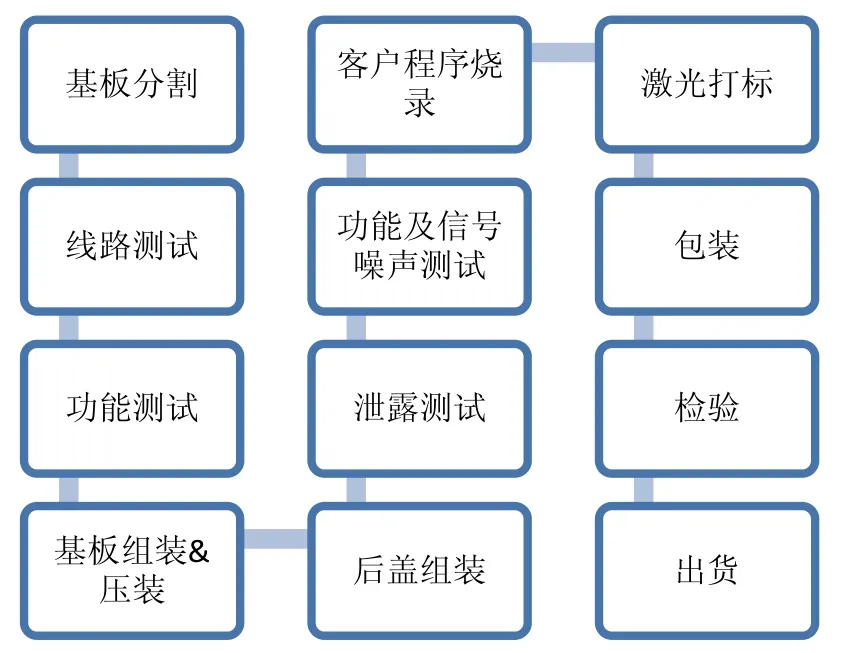
图1 雷达产品生产流程

1.2 产品生产现状

基板组装和压装是雷达产品的重要工艺，其中，需要将两种基板（高频板和低频板）的连接器压装在一起。在压合过程中，需要管控两者接触面的压力。如压力太大，则有可能导致连接器附近的压强过高，基板变形，可能导致附近的其他元件与基板脱离，造成产品功能失效。如压力太小，则有可能出现连接器未能连接成功或不充分连接，造成产品功能失效和潜在风险。压合力的上下限定义为40N和20N，但在生产过程中，发现压合力经常会超过40N，造成大量产品报废。正常压力曲线与非正常压力曲线如图2和图3所示。

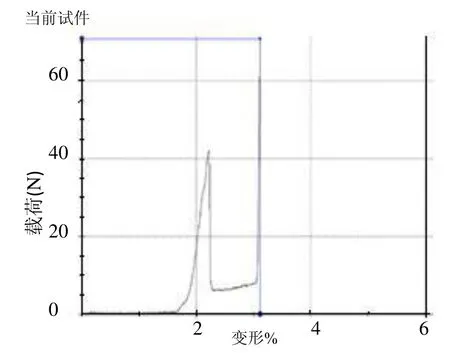
图2 正常压力曲线

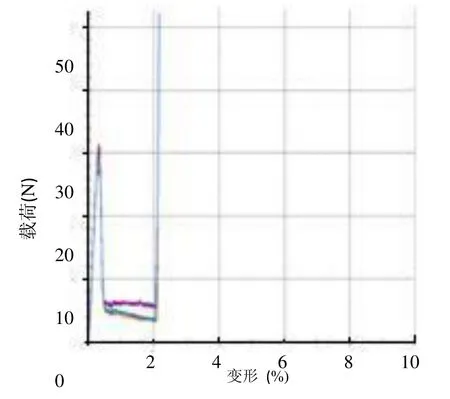
图3 异常压力曲线

2 六西格玛DMAIC改善

2.1 Define界定

基板组装站点中会出现不同的不良形式，不良类型包括基板压合力超40N、pin针弯曲、误报、产品掉落、pin针损坏等，不良结果如图4 所示。其中基板压合力超40N为主要报废原因，占总报废比例43%。本次项目主要着力研究基板压合力超40N的问题。

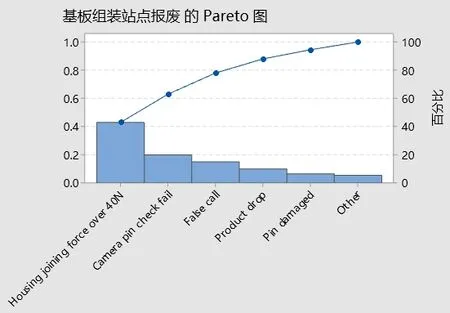
图4 基板组装站点报废分布帕累托图

2.2 Measure 测量

图5为某一天生产所得的压合力数据， 可知压合力满足正态分布，均值为 34.886N，标准差为2.401N，95%的均值置信区间为34.77N到35.002N，50%的数据落在33.29N和36.53N中间。通过压合力的单值移动极差图6可以看出，在连续生产过中压合力的取值经常超出上限，且大多数据比较偏上限，数据波动比较大。

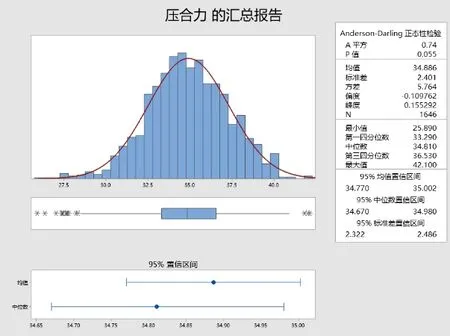
图5 压合力数据汇总图

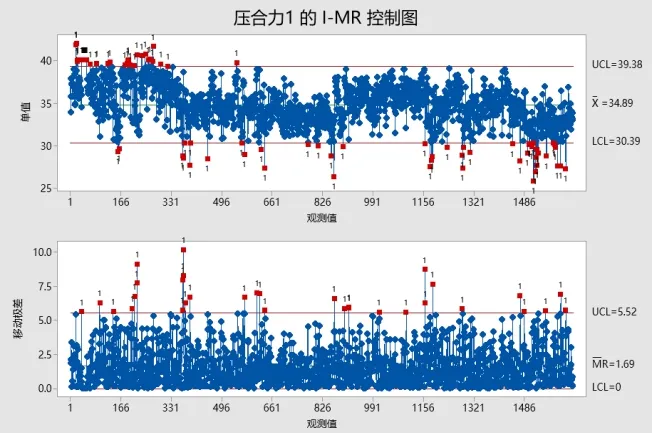
图6 压合力的I-MR控制图

2.3 Analyze 分析

从人、机、料、法、环五个方面分析造成基板压合力超40N失效的原因，经团队分析，主要原因可能是机器方面的问题，决定对机器各项参数进行研究分析。

由图7鱼骨图和头脑风暴得出初步实验方向：机器夹爪位置偏移，向下压力过大，向下压合时速度过快。相关参数有：机器夹爪X轴位置，Y轴位置，向下压力，速度4个参数。

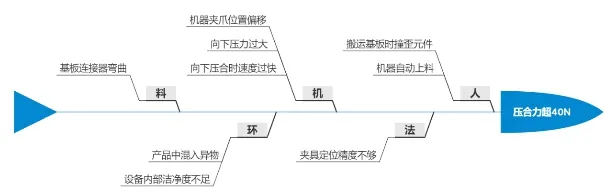
图7 压合力超40N问题的鱼骨分析图

2.4 Improve 改进

2.4.1 设计全因子实验并拟合

每个参数各取两个水平，分析4个因子效应的显著性，如表1所示设置。以此设计全因子实验，形成实验表格并随机排列实验顺序，实验后得到数据见表2和图8正态图、图9 Perato图及图10残差图。

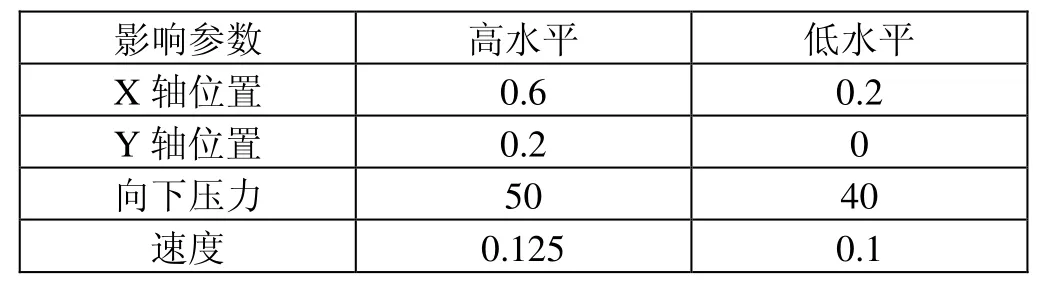
表1 影响参数及高水平和低水平设置

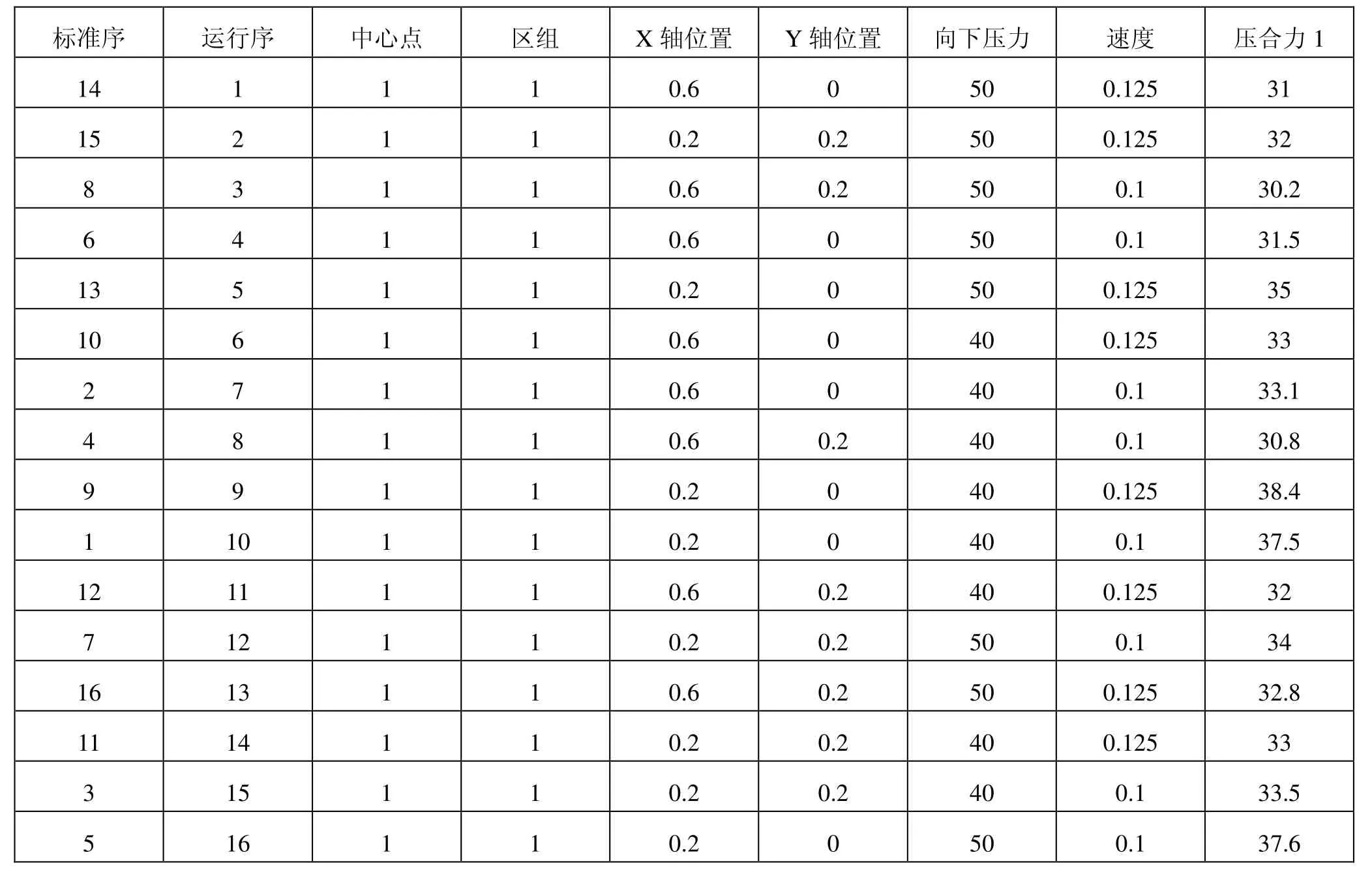
表2 全因子实验结果

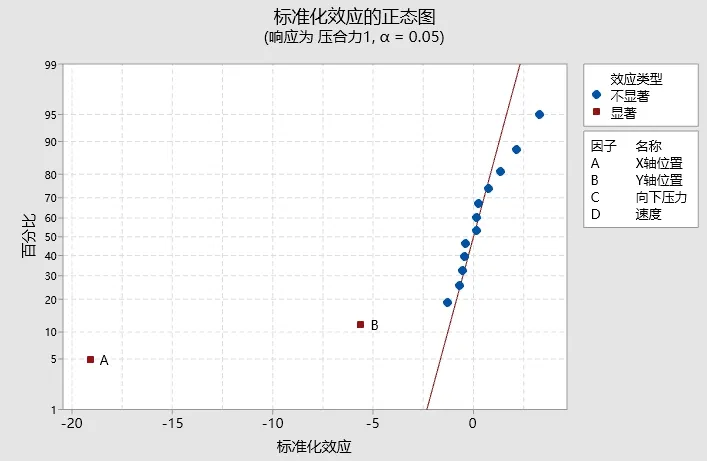
图8 标准化效应的正态图

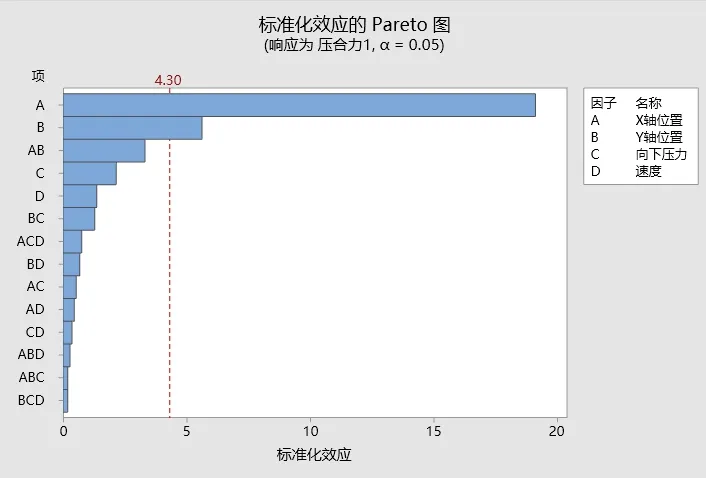
图9 标准化效应的Pareto图

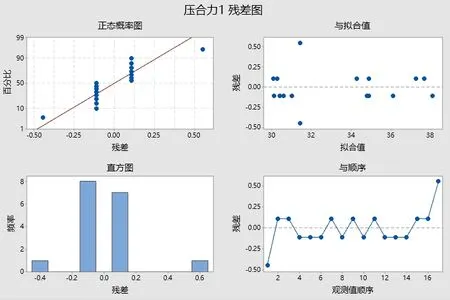
图10 全模型的压合力的残差图

进行残差诊断，从回归结果可以看出，模型的P值为0.033小于0.05，可以判定本模型是有效的。失拟项的P值为0.651大于0.5，显示这里对相应变量压合力的拟合没有明显的失拟。从效应的 pareto图和正态图可以看出，A，B这两项效应是显著的，而其余项都不显著。从残差对于观测值为顺序的散点图可以看出，各点随机地在水平轴上下无规则波动。对于拟合值图，没有出现漏斗形或喇叭形。从残差诊断中看出，模型基本上是好的。在检验各项效应中，发现四个自变量主效应，只有A,B是显著的。交互作用项中，只有AB比较显著。结果如表3和图11所示。

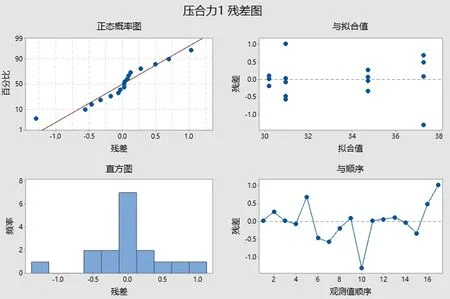
图11 删减模型的压合力的残差图

更改模型，拟合新模型，修改模型中的项，改为 A，B和 AB，重新计算。模型项及二阶交互项的 P值均小于 0.5，表明模型总的来说是有效的。失拟项为0.768大于0.5也表明模型没有明显的失拟。列出全模型和删减模型后的多元决定系数，如表 3所示可以看出 R-Sq（调整）的值由 0.9615提高到0.9630，S的值从0.585855降到0.574255，可见删除不显著的主因子及交互项后，回归的效果更好了。得到回归方程：压合力=40.470-15.850 X - 17.35 Y+22.38 X×Y。

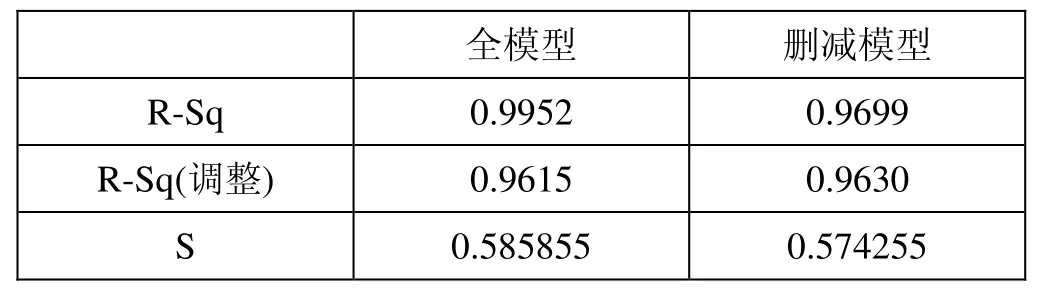
表3 全模型和删减模型的多元决定系数表

2.4.2对选定模型进行分析解释

从主效应图（图12）和交互效应图（图13）中可以看出，因子A和B对于响应变量压合力的影响比较显著，A和B的交互作用此时D为0.97812非常接近 1，表示响应变量对于响应变量的影响也比较显著。由于优化目标压合力属于望目特性，取目标为30N。经过机器计算后，最佳取值为X轴位置为 0.6，Y轴位置为 0.2。可以使得目标值达到30.175N，非常接近设定的目标。根据模型在新设计点处对压合力的预测响应可以看出，95%的置信区间在29.555到30.795之间，可以认为满足本次设定模型的目标。压合力与X、Y轴位置曲面图和等值线图如图14和图15所示。

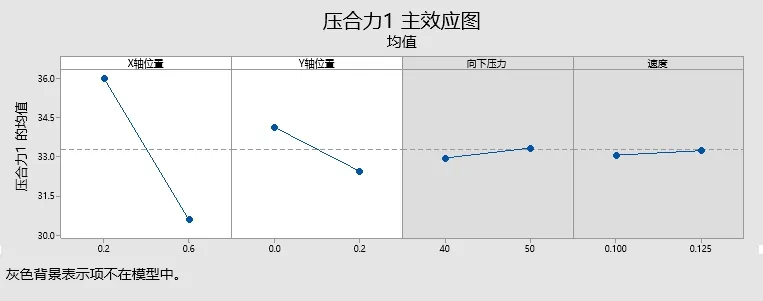
图12 压合力的主效应图

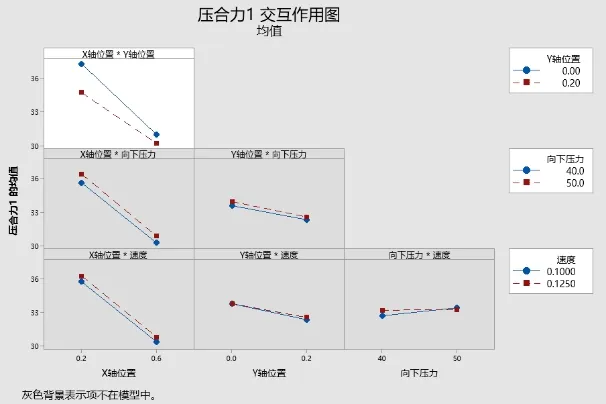
图13 压合力的交互作用图

图14 压合力与X、Y轴位置的曲面图

图15 压合力与X、Y轴位置的等值线图

2.5 Control 控制

得到最佳参数设定后，更改设备参数，机器夹爪位置X轴改到0.6，Y轴改到0.2，进行试跑，得出数据用I-MR控制图如图16所示，结果良好，表明此过程受控。

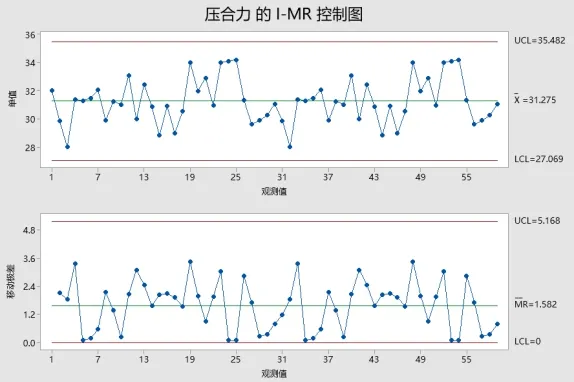
图16 改进后压合力的I-MR控制图

通过Minitab软件分析，得出影响压合力超40N的主要因子为机器夹爪位置，包括X轴和Y轴位置。并通过设计实验，得出最佳参数设定为 X轴位置=0.6，Y轴位置=0.2，通过此设定压合力可以达到期望目标值30N上下，再做一批试跑后压合力的值可以保证在上下限（20N～40N）之内，均值在31.275N左右，达到目标且过程受控。

3 结语

此次六西格玛项目着力于改善产品质量问题，通过DAMIC方法，先界定了造成产品失效的主要问题，分析造成此失效的根本原因，通过 Minitab软件进行定性定量的数据分析，设计多因子实验找出对目标值影响较大的因素，再找出达到目标所需设定的最佳参数水平，经过验证后确认达到此次改进项目的目标。