分形理论下基于时间序列的音乐识别研究

高 莉

(湖北仙桃职业学院 教育学院 ，湖北 仙桃 433000)

音乐存在于人们生活中的各个地方，人们可以用音乐表达内心的情感，同时也可以用音乐进行人与人之间的沟通交流[1].音乐以及其它语言类学科，都属于具有显著代表性的认知模式.随着科学技术的发展，对于音乐的研究不仅仅局限于对音乐的欣赏和分类，更多则是倾向与音乐信号的识别，当前关于音乐信号识别的研究包括很多方向，如音乐搜索查询、音乐生理学和自动生成曲目等[2].

音乐信号的识别不仅可以运用于心理学和生理学[3]，也可以运用于音乐数据库的搜索查询以及自动作曲.互联网信息时代的飞速发展，音乐信号的信息量非常大，音乐的搜索和数据信息的分类非常复杂且困难，要对音乐搜索系统进行智能化升级和高效管理，就需要对音乐信号的特征进行研究，从而对音乐进行正确的分类[4].当前比较通用的歌曲检索方式就是在网站内输入歌曲的名字或者歌词的内容，但是在实际情况中，人们总是会忘记歌曲的名字或者歌词，但是不会忘记曲目的旋律，因此在该种情形下就要对自己能哼出的音乐旋律进行特征分析，从而得到信号特征进而在系统库内进行目标匹配.

基于此，本研究基于分形理论和混沌特性，分析不同音乐曲目的Lyapunov 指数和关联维数，从而判断不同音乐信号的时间序列特征和分形程度，为音乐信号识别的智能化发展提供现实依据.

1 分形理论

1.1 分形理论的质性分析

分形指的是在规定的意义下部分与整体自相似的部分[5].而在相关文献中定义“分形”属于M维空间内的某个点集的集合，在不一样的方向上含有自相似性，而且含有一个不完整位数(小于M)[6].也有学者表明“自相似性”跟“分形”的结构相似，指的是整体同部分的相似之处，在直观方向存在一种构造图，前后2部分仅仅是标度不一样，其余部分的构造方式都相同.观察的部位不管是近处还是远处，得到的结果都一致，学者们就把这种图称作含有自相似的框架.如果在改变图形的尺寸过程中，其余部分的结构并没有改变，此时该图形就叫做分形[7].整体上来说，分形的特性包含3个部分：部分和整体具有相似特质、构造细致和非整数性(关联维数).音乐则可以在空间序列上产生整体同部分的自相似性，而且逐渐地发展成为细致精确的结构，该种含有自相似性构造的现象就叫音乐分形.

关联维数算法把一维序列中的数据组合成为相空间内的n维向量a=(a1,a2,…,An),把向量往后挪动h(h为整数而且是取样间隔)，从而形成n维空间内的不同向量a′=(a1,a2,…,An+h)[8].根据稳定的间隔h向右依次挪动就能够获得相空间内的点集合{ax}x=1,2,…,K,而集合内点的个数可以由K=k-h+1计算得来.

于点集合内随机取一个点当作参考点，以这个点为中心画圆(半径为r)，再统计该圆内除了中心点以外点集合内的其他点数，从而获得关联函数F，如下式所示：

(1)

其中G代表Heaviside 函数.

如果K趋近于无穷大，那么关联函数W是集合内点间距离的概率函数，设此时吸引子伸展量的最大值为D，此时W的表示公式为：

(2)

其中，L2(n,r)属于根n和r相关的常数，L2属于关联函数曲线的斜率.

如果r1和r2之间的相对距离非常小，则L2(n,r)的计算方法如下式所示：

(3)

其中，d为吸引子中的伸展量，如果r非常小，就可以计算出关联维数.若曲线的斜率随着嵌入维数的增大而增大，则说明没有分形的特征.如果曲线的斜率随着嵌入维数的增加而慢慢形成一个稳定值，则表明含有分形的特征.时间延迟h的规定条件有2个：一个是与数据采集时间间隔成倍数关系；另一个是取值要适当，过小会导致获取信息会很困难，过大会导致测量存在较大误差，根据相关文献，h的取值在接近15时，获得的关联维数最合适.

1.2 音乐中混沌现象的特征

音乐属于非线性动态系统[9]，其非线性动态特性内部存在着一定的深层次规律，对其内部规律进行研究可以分成2种序列：时间序列和空间序列.在时间序列上，音乐表现出的形式是由有序慢慢转变成无序，由有序转变成无序的运动序列叫做混沌序[10].关于音乐的非线性解释，一般都是音乐线条的非旋律化，而分形理论的核心特征是：无序性、不平衡性以及不确定性.

在创作音乐作品时，多种音乐现象能组成某种确定的比例关系，如果把某个主题当作作品的起始条件，那么在时间序列以及空间序列轨迹上都会产生一定程度的改变，比如：某段旋律不断重复、逆行和倒影等，接着以特定比例进行扩大和缩小，这些音乐现象都包括在音乐线性过程内.音乐的存在形式很多，包括音乐的基本属性、音乐的一般变现方式、音乐的制作以及演奏，这些都有着复杂的时间序列和空间序列，其时空痕迹的扩散也非常复杂.所以，利用非线性的思维和方式进行音乐的特性分析，能够反应音乐最本质的特征[11].时间序列(混沌序)的特征包括：

1) 边界性 混沌含有吸引域，它的活动范围一般情况下都是特定的，且不会因为混沌内部结构的改变而改变.

2) 普遍性 不同的非线性系统内，混沌序都会含有相同的特质，而且不会因为外界环境的的改变而改变，这就是混沌的基本属性.

3) 分形维度 在同一个空间里的混沌序，其运动轨迹的重合可以表示成分形维度，该分形维度能够分为数个种类，本文使用的分形维度是关联维数[12].

4) 量化特质 对于混沌序，能够运用Lyapunov 指数[13]研究其稳定性，如果该指数比零大，就表明该混沌序不稳定，运动轨迹会根据指数产生分离.该指数的绝对值可以表明序列的混沌程度，距离靠近的点之间，点内部的信息丢失量会因为该指数绝对值的增大而提高，序列或者系统的混沌特性就能够易于被发现.

2 音乐分形实验及分析

2.1 实验准备

1) 实验设备 本研究运用Matlab 构建一个快速数字化乐音仿真模型，该模型基于1组正弦波，经过音色修饰后合成音乐进行播放，其中音色修饰分为音强随时间的自然衰减包络和各谐波成分的能量分配两个部分.运用格式工厂把将 MP3 格式的音频转换成Matlab可以直接读取的WAV 格式，同时利用其截取的功能对音乐片段进行时长截取.

2) 音乐材料 选择3种不同类型的音乐进行分析，分别是钢琴曲、流行乐和哀乐，如下表1所示：

表1 音乐材料性质

3) 音乐信号提取 第1，运用格式工厂把MP3格式的音乐转换成WAV格式，接着进行小节划分和A/D转换.第2，分析混沌特性，根据Lyapunov 指数的大小判断信号是不是含有混沌特性，也就是时间序列.第3，基于关联维数算法判断关联维数，从而分析音乐分形的复杂程度.

2.2 音乐信号划分

本研究选择3首不同的音乐信号进行划分，结果如图1所示.

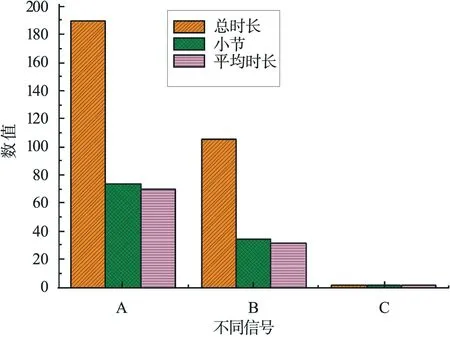
A.《致爱丽丝》； B.《Discotheque》； C.哀乐图1 不同音乐信号划分结果

由图1可以看出，钢琴曲《致爱丽丝》的总时长是 190 s，分成106个小节，每节 1.79 s.流行音乐《Discotheque》的总时长是 74 s，分成35个小节，每节 2.11 s.哀乐的总时长是 70 s，分成32个小节，每节 2.19 s.

2.3 混沌特性和分形程度分析结果

首先，对钢琴曲《致爱丽丝》的混沌特性和分形程度进行分析，结果如图2所示.

图2 《致爱丽丝》不同小节的Lyapunov

由图2可以看出，钢琴曲《致爱丽丝》的Lyapunov 指数上下浮动区间是在[0.02,0.25]之间，而关联维数在[13,17.8]之间.经典钢琴曲的维数起伏非常显著，表明其分形程度比较强烈.钢琴曲的创作难度非常大，同时其创作的过程非常繁琐，这就表示作曲家的能力要很强，特别是针对是经典的钢琴曲.

其次，对《Discotheque》的混沌特性和分形程度进行分析，结果如图3所示.

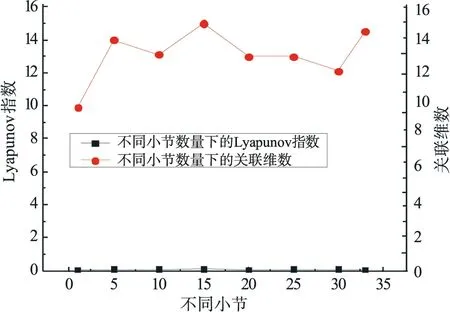
图3 《Discotheque》不同小节的Lyapunov 指数和关联维数

由图3可以看出，《Discotheque》的Lyapunov 指数上下浮动区间是在[0.006,0.008 1]之间，而关联维数在[9.901,15.001]之间.《Discotheque》属于流行曲风，其创作过程相对来说比较简单，但是该曲种的节拍非常强烈，也由非常强的动感，在演奏时音符的改变会充满了随机性，这就导致《Discotheque》的关联维数改变不及钢琴曲显著.

最后，对哀乐的混沌特性和分形程度进行分析，结果如图4所示.

图4 哀乐不同小节的Lyapunov 指数和关联维数

由图4可以看出，哀乐的Lyapunov 指数上下浮动区间是在[0.052,0.159]之间，而关联维数在[9.997,16.987]之间.哀乐一般是表示对逝者的思念和沉痛心情，其节奏的改变都是在相应的范围之内，主题的表达非常简单，主要就是为哀痛和不舍，所以哀乐的关联维数改变程度最低.

2.4 不同差分后的关联维数

为了保证关联维数的稳定性，对3种曲目的音乐信号进行差分求解，结果如图5所示.

由图5可以看出，在进行不同阶数的差分以后，不同曲目信号的关联维数都在不同阶数下的波动非常微弱，因为试验过程存在一定的误差，因此可以认为，不同阶数下关联维数基本没有改变，说明不同曲目信号内的分形程度具有稳定性.

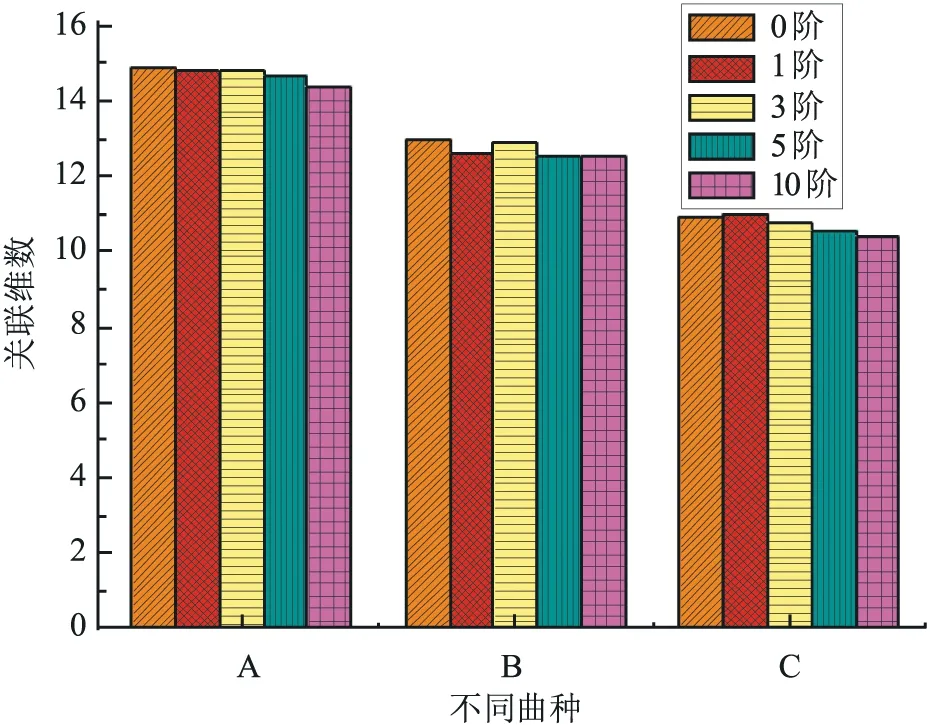
A.《致爱丽丝》； B.《Discotheque》； C.哀乐图5 不同差分阶数下的曲目关联维数

3 结语

本研究为了对不同性质的曲目音乐分形的复杂程度进行分析，通过对钢琴曲、流行乐和哀乐进行音乐信号分析，根据Lyapunov 指数的大小判断信号是不是含有混沌特性(时间序列)，并根据关联维数算法判断关联维数，从而分析音乐分形的复杂程度.从结果来看，钢琴曲的分形程度最高，流行乐次之，哀乐的分形程度最低，而不同曲目内的信号分形程度具有稳定性.本研究也存在一定的不足之处，选择曲目的种类比较少，这会对文章结果的普适性产生一定的影响，这也是文章下一步研究需要改进的地方.