通信协议离散事件系统故障的时间可诊断性分析
2021-09-10汪恒宇张信哲刘久富
汪恒宇,张信哲,刘久富
(南京航空航天大学 自动化学院,江苏 南京 211106)
故障可诊断性解释了故障诊断深层次的内涵,为从根本上提升控制系统对故障的诊断能力的研究提供了理论依据.对系统可诊断性进行分析,从系统层面对系统结构进行优化,可以提高系统对故障信息获取、分析能力,从而更加有效地提升系统的安全性[1].Hashtrudi等[2]在自动机建模的时延DES背景下介绍了时间可诊断性的概念,在他们的事件中包含一个全局时钟的标记,同时是可以观测的.时间可诊断性要求通用故障的点火fi在至多τi次标记后可以被检测和隔离.TripaKis在[3]中提出了带保护的时延自动机,δ诊断性(基本上和我们的τ诊断性定义是一样的概念的)提出和证明是在区间δ∈Q上PSPACE完全问题.对时间的明确考虑对于运输系统、通信协议、电路、航空系统或实时系统等系统的规范和验证至关重要,是否可以通过观察有限长度的词来重构故障事件的发生.
通信系统在出现故障的时候就会导致数据传输不确定或者不完整,或者还会导致丢失关键信息,同时通信系统存在数据交换复杂,无法全面监测,故障征兆不明显,实际故障数据捕捉存在困难等问题,所以如何快速、可靠地对通信系统进行故障诊断保证数据传输安全完整是一个有待解决的问题[4-5].
早期通信系统的数据分析方法主要依靠人工参照协议规范分析数据的有效性、正确性和数据的逻辑是否正确.近年来各种系统的网络化互联,系统复杂性的增加导致了大量的不确定性,这种方法层出不穷,如基于模型的不确定非线性大型网络系统分布式故障诊断方法[6],结合粗糙集和贝叶斯网络的电力信息通信系统快速故障诊断方法[7],通过内建的自我测试和一个packet/flit比较模块,分别嵌入网络适配器和路由器的在线搜索、故障检测和故障定位方法[8],基于模糊集的动态故障树方法评价数据通信系统[9]等.文献[10]建立随机Petri网(SPN)表示的CTCS无线通信机制模型和列车与无线闭塞中心通信的GSM-R故障恢复模型,给出对通信故障定位的方发.文献[11]提出了一种有效的移动网络混合故障诊断协议,采用网络编码技术来交换诊断信息,从而提供了一个完整概率较高的正确诊断.
本研究考虑故障变迁序列的逻辑模糊并对变迁节点添加点火时间区间,提出了一种基于部分可观时间Petri网的时间可诊断性分析方法,利用多项式时间算法求解多路径的LPP确定系统中不可观故障的时间可诊断性,在时间维度对不可观系统故障进行可诊断性分析,可评估系统的时间可诊断程度,为后续的系统故障诊断提供一定的理论依据[11-25].
1 部分可观时间Petri网的时间可诊断性
1.1 部分可观时间Petri网
定义1 部分可观Petri网(partially observed petri nets,POPN)定义为一个6元组NPOPN=(P,T,Pre,Post,To).其中⟨P,T,Pre,Post⟩是基础PN模型,P为元素总数为m的库所集合(Place),T为元素总数为n的变迁集合(transition),To⊆T是可观变迁集,满足|To|=0≤no≤n.Pre∈Nm×n、Post∈Nm×n分别为变迁的前向弧矩阵和后向弧矩阵,定义矩阵C=Post-Pre,C∈Nm×n为POPN的关联矩阵(N为非负整数集).
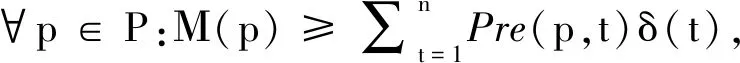
其中C(p,t)=Post(p,t)-Pre(p,t),同时简写为Μ[δ〉Μ′.
定义2 时间Petri网(time petri nets systems, TPN)定义为NTPN=(P,T,Pre,Post,Q),其中N=(P,T,Pre,Post)定义了网络结构PN,Q:T→Q×(Q∪∞)定义了与变迁相关联的静态间隔集.给定一个变迁ti∈T,函数Q将两个有理数与ti(第二个也可能是∞)相关联,即Q(ti)=(li,ui),其中li≥0,ui≥li,li≠∞.当且仅当变迁在时间区间[li,ui]中逻辑使能时,变迁ti点火.
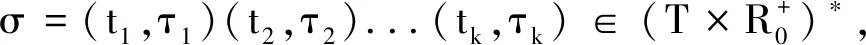
如果存在一个Μ0[σ⟩Μ的TTS序列σ,则标注Μ在⟨NTPN,Μ0⟩上是可达的.从Μ0可达的所有标注集定义了时间可达集⟨NTPN,Μ0⟩,用Rt(NTPN,Μ0)表示.Rt(NTPN,Μ0)是基础的非时延PN可达性集的子集.如果存在一个的正整数k,满足所有Μ∈Rt(NTPN,Μ0),Μ(p)≤k,TPN系统⟨NTPN,Μ0⟩是有界的.
定义3 部分可观标签时间Petri网(partially observed labeled time petri nets systems, POLTPN)定义为NPOLTPN=(NPOPN,Q,L),标签函数L:T→L∪{ε}为每个变迁分配一个标签L或空符号ε.
1.2 时间可诊断性问题
∀σ∈∑(σo,τeh),|σ|≥|σo|,
其中τeh为满足L(ti)=γeh且最后触发变迁的点火时间信息,|σ|为TTS序列中包含的变迁个数,|σo|为TLS序列中包含的变迁个数.同时存在为σu={ti∈Tu}∈σ的TTS序列中的不可观子序列且L(σu)=ε,|σ|=|σo|+|σu|.
若L(σ)=L(σo),忽略点火时间信息有log(σ)=σu1t1σu2t2…σuktk(k≥1),可观子序列为log(σo)=t1t2…tk,其中ti∈To,i=1,2,…,k;不可观子序列log(σu)=σu1σu2…σuk,σui为可观变迁ti-1和ti之间点火的不可观变迁序列.
C(Μ0,σo,τp)={Μ∈Nm|Μ0[σ>Μ,σ∈∑(σo,τeh)}.
(1)
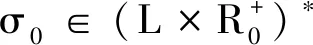
S(Μ0,σo,τp)={Μk,Θk|Μk∈C(Μ0,σo,τp)}.
(2)
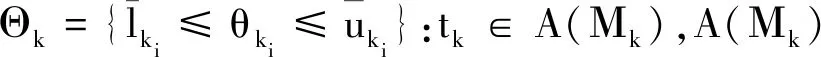
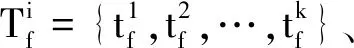
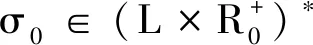
∀σ∈∑(σo,τeh),tf∉σ,Diag(σo,tf,τ,τp)=1,
如果没有关于任意故障集i∈{1,…,r}的不确定状态,那么TPN是τ时间可诊断的(对于任何τ∈R+都成立).
定理1 〈NTPN,Μ0〉为标签函数是L的标签TPN系统,其中NTPN=(P,T,Pre,Post,Q).假设〈NTPN,Μ0〉是底层逻辑标签PN系统.如果〈NTPN,Μ0〉是可诊断的,那么∃τ′∈R+以致〈NTPN,Μ0〉对于任意τ≥τ′是τ可诊断的.
证明:计时结构的影响只能是在底层逻辑模型中启用的禁用序列.相反,不会出现TPN中具有发生权的序列在底层逻辑PN中不具有发生权的情况.因此如果底层逻辑PN系统可诊断,总会存在一个正实数τ′以致TPN系统τ′可诊断,因此对于任意τ≥τ′也是τ可诊断的.
2 部分可观时间Petri网的时间可诊断性分析方法
2.1 部分可观时间Petri网的可诊断性分析方法
部分可观时间Petri网估计系统故障状态需要根据变迁的时间属性构建MSCG图,计算与MSCG同构的非确定型自动机G,遍历MSCG图中满足可观变迁触发序列的路径是否包含故障变迁,估计系统故障状态.
G的每个状态对应于MSCG的一个集.边缘用MSCG边缘的第二个元素标记,即与变迁相关的标签.
给定一个TTS集合σ=(ti1,τ1)(ti2,τ2)…(tik,τk)对应的MSCG路径:
(3)
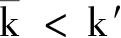
(4)
式中,out(Cq)为状态集合Cq的下边界;Δl表示一个变迁所用时间,这个时间包括:准备触发变迁所用时间、变迁触发所用时间、变迁触发后在下一个库所内停留时间.给定路径π不满足约束条件,则该路径不可能触发.
公式(4.1)到公式(4.4)对序列的总长度施加限制.
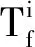
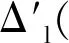
公式(4.10)表示2个序列的可观察测得变迁σ和σ′同时瞬间发生.
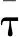
定理3 存在关于一些故障集i∈{1,…,r}的状态∀σ∈∑(σo,τeh),tf∈σ:
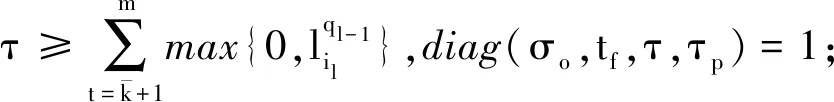
证明:考虑故障发生后变迁的所有时间约束上限,如果τ大于或等于下限之和,即时间持续到观测序列结束且可通过可观变迁进行故障分析,那么故障集是τ时间可诊断的,否则不是关于故障集i的τ时间可诊断.
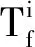
1)σ和σ′有相同的可观测投影,即L(σ)=L(σ′);
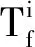
证明:当存在包含故障变迁的序列和不包含故障的序列对应相同的观测序列,满足故障发生后经过时间τ到达最后的可观变迁,此时为不确定状态不能判断故障状态,所以故障不是τ时间可诊断的.
2.2 基于MSCG的时间可诊断性分析算法描述
输入 POLTPN模型,检测时间点τp,故障变迁tf,时间τ.
输出 故障诊断结果diag(σo,tf,τ,τp)∈{0,1}:
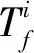
1) 头节点C0→M0,tag(C0)=new,C0→∑(C,M),
2) while ∃tag(C)=new∈∑(C,M) do
新节点tag(Ck)=new
for 任意ti∈A(Mk) do
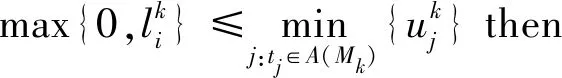
Mk[ti>Mk+1,Ck+1→Mk+1
for ∀tr∈A(Mk) do
ifMk[tr>Mk+1then
else
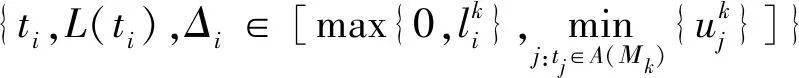
ifCk+1∈∑(C,M)then
tag(Ck+1)=exit
else
tag(Ck+1)=new,Ck+1→∑(C,M)
取消新节点标记tag(Ck)=exit
3) 取Ci→∑(C,M)和ti∈A(Mk),Mk∈∑(C,M) 构建MSCG图
4) 搜索满足σo=ε,τp=0且满足公式(4.1)、(4.2)、(4.6)和(4.7)的路径放入∑(ε,φ)
5) 搜索标签时间序列σo=(γe0,τe0)(γe1,τe1)…(γeh,τeh)的路径σ并放入∑(σo,φ),φ表示不考虑检测时间点τp
6) 给定检测时间点τp,令所有同时满足公式(4.1)、(4.2)、(4.6)和(4.7)且σ∈∑(σo,φ)的σ放入集合∑(σo,τp)
7) fori=1,…,rdo
Diag(σo,tf,τ,τp)=1
Diag(σo,tf,τ,τp)=1
else
Diag(σo,tf,τ,τp)=0
if满足公式(3.4).
thenDiag(σo,tf,τ,τp)=0
elseDiag(σo,tf,τ,τp)=1
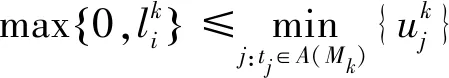
修改后的状态类图是一个有向图,其节点称为集.每个集与网络的一组状态相关联,即可达标签M∈Rt(Nd,M0)和一组定义相对于在M处使能的所有变迁的时序约束的不等式Θ.边界集合为(t,L(t),Δ∈[l*,u*]),其中t∈T是从尾节点中的标签引导到头节点中的标签的变迁;L(t)是与t相关的标签函数,Δ∈[l*,u*]是对从边缘尾节点到边缘的头节点的时间约束,l*≤l和u*≤u.
给定有界时间Petri网系统
2.3 算法复杂度分析
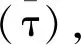
3 实例分析与验证
3.1 通信系统POTPN模型构建
通信系统基本由信息源,发送设备,信息,接收设备,受信者等组成.其工作原理为发送的数据信息被分成多组在多个支路上传输,进入缓冲区后收集数据包以重构原始信息,并向发送方发送确认信息[13].图1以通信系统工作过程中关键节点为库所,关键动作为变迁建立时间Petri网模型,模拟通信协议工作过程,各库所、变迁含义如表1、表2所示.
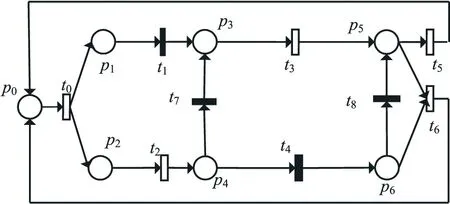
图1 通信系统Petri网模型

表1 各库所物理含义
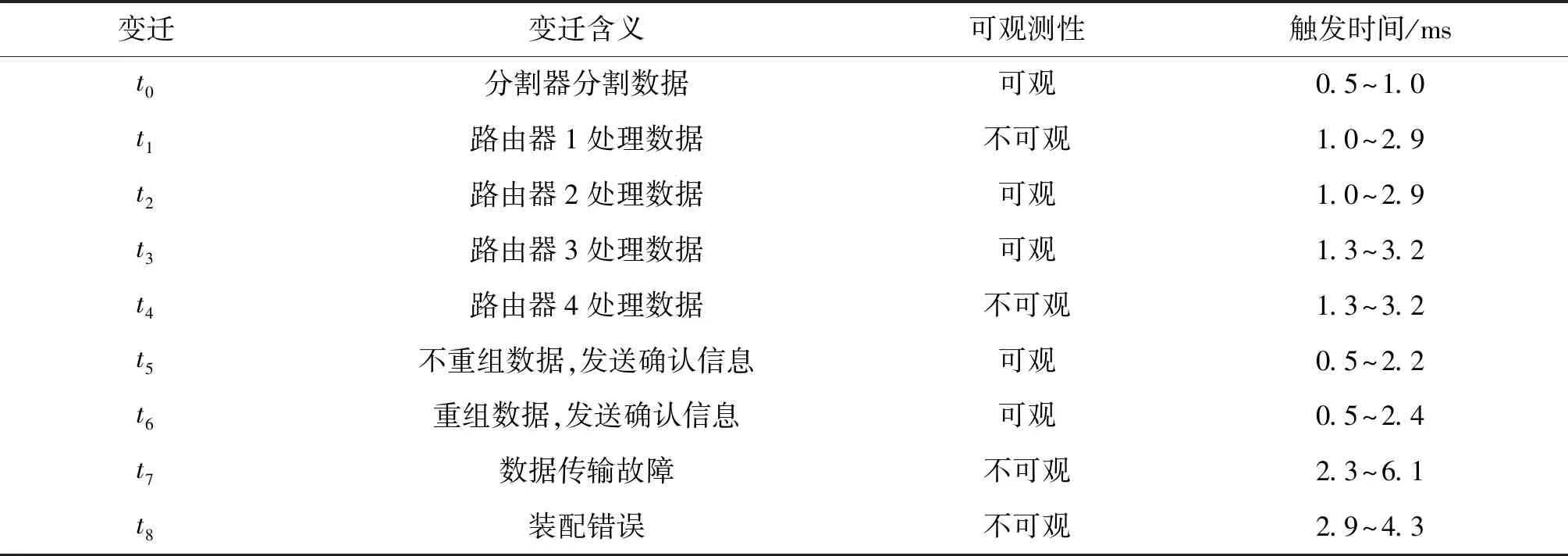
表2 各变迁物理含义、可观测性及设计动作时间
3.2 通信系统故障的时间可诊断性分析
通信系统工作过程为:发送方的数据准备传输(p0),分离器把数据分成两组并打包(t0),打包数据在2个信道上传输,经过信道1经过路由器((p1,t1;p2,t2)和信道2经过路由器(p3,t3;p4,t4) 进入缓冲区(p5,p6)后收集数据包以重构原始信息,并向发送方发送确认信息(t5,t6).
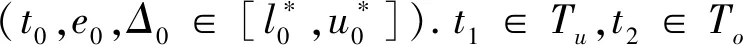
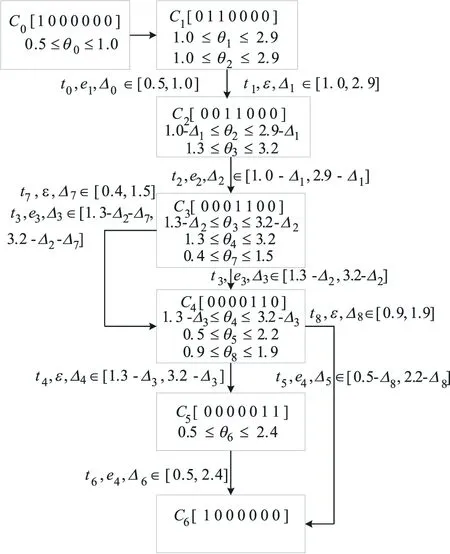
图2 通信系统的MSCG图
表3中为多次系统故障的时间可诊断性分析结果,时间检测点为4.0时间τ=3时标签时间序列为σo=(e1,0.7)(e2,3.6),搜索满足σ∈∑(σo,4.0)的TTS有3条,Δ0+Δ2=2.9,Δ0+Δ1+Δ2=2.9,Δ0+Δ1+Δ3+Δ2=2.9,对于∀σ∈∑(σo,4.0)路径不经过故障变迁,由定义7得到该标签时间序列是3个时间单位内可诊断的.时间检测点为5.0时间τ=2时观测序列为σo=(e1,0.8)(e3,3.1)(e2,4.8),搜索满足σ∈∑(σo,5.0)的TTS有1条,Δ0+Δ1+Δ3+Δ2=4.0对于∀σ∈∑(σo,4.0)路径不经过故障变迁,则该标签时间序列是2个时间单位内可诊断的.

表3 通信系统故障的时间可诊断性分析结果
时间检测点为7.0,观测序列为σo=(e1,0.8)(e2,2.5)(e3,6.1),搜索满足σ∈∑(σo,7.0)的TTS序列有8条,有故障存在的TTS有4条,所有TTS满足∑Δ′=5.6,选择序列log(σ)=t0t1t2t7t4t3对应的时间消耗为∑Δ′=Δ0+Δ2+Δ7+Δ4+Δ1+Δ3=5.6,通过公式(3.4)求解多路径的LPP问题得到从故障t7开始到下一个可观变迁最短时间为Δ7+Δ4+Δ1+Δ3=3.6,则故障变迁t7不是3个单位时间内可诊断的,是4个单位时间内可诊断的.
时间检测点为8.0,观测序列为σo=(e1,0.7)(e2,2.6)(e3,5.9)(e4,7.4),搜索满足σ∈∑(σo,8.0)的TTS序列共10条,有故障存在的TTS有5条,所有TTS满足∑Δ′=6.7,其中log(σ)=t0t1t2t4t3t8t5对应时间消耗为∑Δ′=Δ0+Δ1+Δ2+Δ4+Δ3+Δ8+Δ5=6.7,从故障t8开始到下一个可观变迁最短时间为Δ8+Δ5=1.5,则故障变迁t8不是1个时间单位内可诊断是4个单位时间内可诊断的.
3.3 仿真验证
为进一步验证POLTPN模型的时间可诊断分析方法,对多类不可观故障进行模型构建并进行多次仿真,如表4所示.分别对故障变迁的时间可诊断性进行 1 000 次设定:900次可诊断、100次不可诊断.900次可诊断实验中,算法实际诊断出887次可诊断、13次不可诊断;100次不可诊断实验中,算法实际诊断出98次不可诊断,2次可诊断.可诊断分析准确性为98.5%,不可诊断准确性为98.0%.实验说明本研究的时间可诊断性分析方法能够对POTPN模型中故障的时间可诊断性进行有效确定.

表4 算法运行1 000次后系统行为统计结果
4 结语
1) 本文结合多项式时间算法求解LPP和修正状态类图(MSCG)标签时间序列的搜索方法提出了故障变迁的时间可诊断性分析方法.搜索MSCG图中所有满足时间标签序列集合σo的TTS序列σ并求解多路径的LPP问题分析系统是否在给定时间内可诊断.
2) 对不确定状态的故障变迁添加时间信息,考虑故障变迁序列的逻辑模糊,在时间角度对系统故障的可诊断性进行分析.补充了故障可诊断性分析基础.
3) 建立通信协议离散事件系统的部分可观标签时间Petri网模型,根据组件之间触发关系修正相应变迁时间约束,通过构建MSCG图重构故障变迁的发生,通过本文提出的算法诊断是否能在一定时间内诊断出系统故障状态.模拟多类多次故障变迁验证了算法的有效性.
本文算法依赖于MSCG图的复杂性和LPP求解的,如果系统演算比解决LPP所需的时间快,或者遇到高复杂性系统时,则算法会出现局部有效性问题.所提方法还需进一步改进.本文仅考虑了变迁时间序列的逻辑模糊情况,对时间模糊没有明确考虑,忽略了变迁同时触发的情况,将对构建的MSCG的边界条件和状态集进一步修正来适应时间模糊的情况.
