一类含(p,q)-Kirchhoff型双调和方程组的多解性研究
2021-09-10张琪,缪清
张 琪,缪 清
(云南民族大学 数学与计算机科学学院,云南 昆明 650500)
主要研究包含(p,q)-Kirchhoff型方程组
(1)

(M)存在2个正常数m0,m1,对于所有的t≥0有m0≤Mi(t)≤m1.
函数F,G:Ω×2→满足F(x,s,t),G(x,s,t)对所有(s,t)∈2在点x都可测且对于几乎处处x∈Ω有(s,t)为C1.Fu,Fv分别是F对u,v的偏导数,Gu,Gv分别是G对u,v的偏导数.假设F(x,s,t),G(x,s,t)满足如下条件:


问题(1)与Kirchhoff[1]研究的弹性弦方程
(2)
有关,这个方程考虑了弹性弦在振动过程中的长度变化影响,推广了D’Alembert的弹性管柱自由振动方程.随着研究的深入,问题(2)转化为
(3)
在文献[2-8]中,问题(3)已经得到了很多研究.
Hssini等[9]基于Bonanno临界点定理[10]研究了一类带Navier边值条件的(p,q)双调和方程问题,后来Allaoui等[11]把文献[9]推广到变指数双调和算子方程组.随着临界点理论在各个领域的广泛应用,许多学者在4阶边值问题方面进行了深入的研究,文献[12-15]研究了4阶边值问题解的存在性和多解性.其中,在文献[12]中,Hssini等基于Ricceri变分原理[16]研究了4阶Kirchhoff型问题
(4)
解的存在性和多值性.随后,肖虹兆等[17]对问题(4)做了推广,利用Ricceri多解定理研究了(p1,p2,…,pn)-Kirchhoff型问题的多解性.
近年来Ricceri 3临界点定理[18]越来越广泛的被用于解决4阶边值问题,例如,Li等[19]研究了(p,q)双调和算子方程问题
(5)
在文献[20-21]中,Ricceri三临界点定理也用于解决 (p,q)-Kirchhoff型问题
(6)
但目前为止根据Ricceri 3临界点定理研究带Navier边值条件的(p,q)-Kirchhoff型的双调和问题的结论甚少,因此,受以上研究的启发,本文根据Ricceri 3临界点定理,证明了(p,q)-Kirchhoff型方程组(1)至少有3个解存在.
1 预备知识
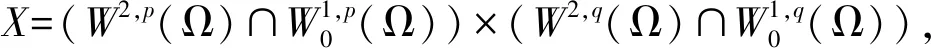
记
(7)
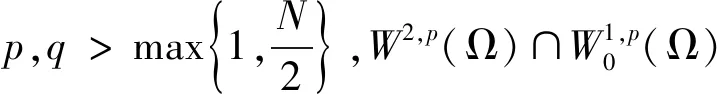
我们称(u,v)∈X是问题(1)的弱解如果对任意(ξ,η)∈X有
(8)
定义泛函H:X→为
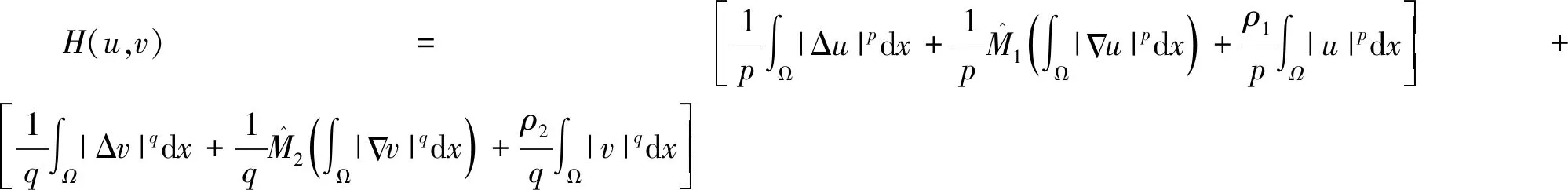
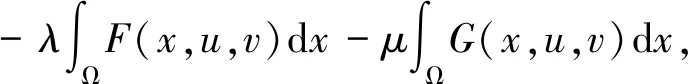
(9)

(10)
通过假设(M),(F),(G)可得H∈C1(X,),同时,求问题(1)的弱解就转化为求泛函H的临界点问题.
设x0∈Ω,选择R2>R1>0使得B(x0,R2)⊆Ω,其中,B(x0,R2)={x∈N||x-x0| (11) 定义 (12) (13) 引理1.1[21]假设(M),(F),(G)成立.设∀(u,v)∈X有 那么,Φ:X→是连续Gateaux可导且序列弱下半连续,在X的每个有界子集上有界,其Gateaux导数在X*上有连续逆.Ψ,J:X→是连续Gateaux可导,其Gateaux导数是紧的. 对(u,v),(ξ,η)∈X,有 定理1.2[18]设X是一个自反的实Banach空间.Φ,Ψ:X→是连续Gateaux可导泛函.其中,Φ是序列弱下半连续且在X的每个有界子集上有界,其Gateaux导数在X*上有连续逆,Ψ的Gateaux导数是紧的,I⊆是一个区间.假设对λ∈I,有 (14) 并且存在h,使得 (15) 成立.那么存在一个开区间Λ⊆I和一个正实数ρ,对每个λ∈Λ和每个C1且有紧导数的泛函J:X→,存在δ>0使得对每个μ∈[0,δ],方程 Φ′(u)+λΨ′(u)+μJ′(u)=0, 在X上至少有3个解且其范数小于ρ. 命题1.3[21]设X是一个非空集合,Φ,Ψ是X上的2个实函数.假设存在r>0,u0,u1∈X使得 (16) (17) (h1)对几乎处处x∈ΩB(x0,R1)和所有(s,t)∈[0,d]×[0,d]有F(x,s,t)≥0; (h3)对几乎处处x∈Ω和所有(s,t)∈2有F(x,s,t)≤α(x)(1+|s|γ+|t|β); (h4)对几乎处处x∈Ω有F(x,0,0)=0. 那么,存在一个开区间Λ∈[0,+∞)和一个正实数ρ有如下性质,对∀λ∈Λ,∃δ>0, 使得,对∀μ∈[0,δ],问题(1)至少有3个解,且其范数小于ρ. 引理2.2假设(M),(h1),(h2)成立.那么∃(u*,v*)∈X,使得Φ(u*,v*)>r, (18) 证明设 (19) (20) 由(M),(13)可知 (21) 同理, (22) 显然,0≤u*≤d,0≤v*≤d,根据条件(h1),(h2),(22) (23) 定理2.1的证明由(M),(h3),(21),对∀(u,v)∈X有 其中,C1,C2是常数且C1,C2>0.由于γ (24) 由引理2.2知,∃(u*,v*)∈X,使得Φ(u*,v*)>r>0=Φ(0,0), 设(u,v)∈X使得Φ(u,v)≤r,从(7)可得 (25) 那么, (26) 从而, (27) 因此,从(18)和(27)有 (28) (29) 由命题1.3对每一个满足条件 (30) 的h,存在r>0,(u0,v0)=(0,0),(u1,v1)=(u*,v*)使得Φ(0,0)=0,Ψ(0,0)=0,并且从(21)和(29)可得 (31) 因此,I=[0,+∞).由(24)和(31)知定理2.1的所有条件都满足,定理2.1即得证.故问题(1)至少有3个解存在.
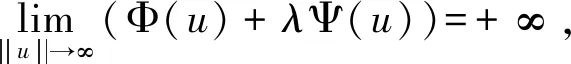
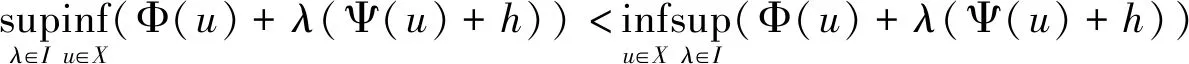

2 主要结果及证明