昆明市月降水量的预测分析研究——基于SARIMA模型和Holt-Winters相加模型

吴万勤,钱 红

(1.云南民族大学 数学与计算机科学学院， 云南 昆明 650500; 2.云南师范大学文理学院 信息工程学院 ，云南 昆明 650231)

降水的分布与人类的生产生活密切相关，对社会、经济和生态环境影响显著.降水量在时间和空间上的非均匀分布，很大程度上决定了洪涝、干旱和暴雨等气象灾害的强度，导致区域干旱事件的频繁发生，地区水资源的严重短缺，以及洪涝和地质灾害的加剧.昆明市位于我国云南省低纬高海拔地区，在云贵高原的中心.昆明市近年干旱已成常态，影响了中药产业，还给当地的花卉产业带来了损失.科学准确的降水预测，可以使农业、水利等有关部门及时采取措施，防止旱涝灾害，降低不必要的损失.因而对昆明市降水量做出合乎实际的预测就显得十分重要.

时间序列分析法对降雨量的预报有较高的精度,并且操作较方便, 所以该方法在降水量分析中运用逐渐普遍起来.冯子溪[1]在基于马尔科夫链与灰色模型的昆明市降雨量预测中利用马尔科夫链与灰色模型相结合的方法建立了合理的模型对昆明市的年降雨量进行了预测[1]；程敏等[2]基于时间序列模型对济南市降水量进行预测分析[2]；宫晨[3]在基于ARIMA模型的拉萨降水量时间序列分析与预测中利用ARIMA模型对其进行建模和预测[3].王超华等[4]分别建立MA-GARCH模型和MA-EGARCH模型对降水量进行分析和预测[4].本论文主要针对昆明市月降水量进行分析和预测，基于2000—2019年昆明市月降水量数据拟合建立模型和相加模型，对2019年1—12月降水量数据预测，采用实际值与预测值误差对比，验证2种模型预测效果.相加模型预测精度相对较高，利用相加模型对昆明市月降水量进行3年预测，并分析预测结果.该模型对昆明市降水量短期预测中有一定参考价值.

基于中国统计年鉴，通过对2000—2019年昆明市月降水量数据分析，可以看出降水量数据具有周期波动性，并且以年为周期，可以明显看出干、湿两季，夏季降水量较多，冬季较少.

1 基于SARIMA模型的短期预测

1.1 SARIMA模型

具有如下结构的模型称为求和自回归移动平均模型，简记为ARIMA(p,d,q)模型：

(1)

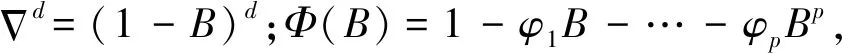
d阶差分后序列可以表示为：

(2)

SARIMA模型建模步骤：

①观察时间序列周期，确定周期长度S.

②通过差分保证时间序列的平稳性，确定d值.

③通过自相关和偏自相关图确定非季节性模型p、q值.

④通过差分平稳后的序列图，自相关和偏自相关图确定季节模型D、P、Q值.

⑤将选定的p、q、d和P、Q、D的可能值代入SARIMA模型.

⑥根据Akaike信息准则(AIC)最小值和t检验选取最优模型[5].

1.2 月降水量数据平稳化预处理

由于昆明市月降水量数据具有明显的周期波动性，表现出明显的年度周期特征，为非平稳序列.对于季节性波动稳定的序列，为了提取季节波动信息，通常使用步长为周期长度的差分运算[6].鉴于此，本文对所研究的数据进行1阶步长为12的差分运算.通过对差分运算后数据的时序分析.可以得出，1阶12步差分可以较好地提取周期信息， 1阶12步差分运算后序列呈现出明显的平稳性.通过统计学分析，数据符合ARIMA乘积季节模型对平稳性的要求.

1.3 SARIMA模型的建立

模型的建立需要进行定阶和定参.

模型的定阶其实就是确定ARIMA(p,d,q,P,D,Q)S模型适当阶数，即p,d,q,P,D,Q的数值.由于对降水量数据进行了1阶差分和周期为12的差分，因此d=D=1.基于一阶12步差分后的自相关和偏自相关分析，1阶12步差分后的序列，除了一阶自相关系数在2倍标准差范围外，其他阶数的自相关系数都在2倍标准差内，偏自相关系数拖尾.因此取p=0，P=0，q=1或2再观察季节性趋势，可以看出，自相关系数每一季节效应周期(12阶)都在2倍标准差外，因此取Q=1或2[6-7].

得到的模型如下:

ARIMA(0,1,1)(0,1,1)12，ARIMA(0,1,2)(0,1,1)12，ARIMA(0,1,1)(0,1,2)12，ARIMA(0,1,2)(0,1,2)12.得到相关模型估计结果和检验结果.各个模型检验结果如表1.

由表1可知，仅有模型ARIMA(0,1,1)(0,1,1)12的参数均通过t检验.故选择使用ARIMA(0,1,1)(0,1,1)12模型对昆明市降水量数据进行建模和预测.对该模型ARIMA(0,1,1)(0,1,1)12进行最小二乘法估计，估计结果为：

表1 模型检验结果

(1-B12)xt=(1-0.949 875B)(1-0.911 362B12)εt.

(3)

为了检验模型的有效性.运用时间序列分析软件建立残差的自相关图，对残差进行纯随机性检验.经过统计学分析表明拟合模型是有效的[5].经过t检验，模型ARIMA(0,1,1)(0,1,1)12的参数统计量P值均小于显著性水平(α=0.05).

1.4 SARIMA模型预测

该论文利用2000—2018年昆明市月降水量的数据，对2019年1—12月降水量数据进行预测,结果如图1，图中2S.E为二倍标准差曲线.

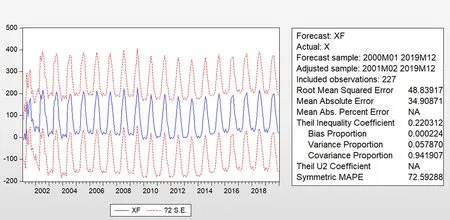
图1 拟合图

结果表明：预测值均在2倍标准差的置信范围内，可根据Theil不相等系数为0.220 312，以及协方差比例为0.941 907，得到模型的预测结果较为理想，预测效果较好[8].

通过预测值与实际值对比(见图 2)，图中X为降水量的实际值，XF为预测值.可以看出该模型拟合较好.

图2 预测值与实际值对比图

2 基于Holt-Winters加法模型的短期预测

2.1 Holt-Winters加法模型

Holt-Winters季节指数模型包括：Holt-Winters乘法模型和Holt-Winters加法模型2种.

对于Holt-Winters加法模型，序列通常可以表达为如下模型结构：

(4)

式中，{y}表示降水量序列，a为常数项；b为长期趋势；c为加法模型的季节因子，t表示样本取值时间，t+k表示将要预测的时期.a,b,c3个系数大小通过以下推倒公式来确定：

a(t)=α(yt-ct(t-s))+(1-α)(a(t-1))+b(t-1)，b(t)=β(a(t)-a(t-1))+1-βb(t-1)，ct(t)=γ(yi-a(t+1))-γct(t-s)，

(5)

其中，α，β，γ是3个平滑因子；s表示周期长短.

对于Holt-Winters乘法模型，序列通常可以表达为如下模型结构：

(6)

式中，{y}表示降水量序列，a为常数项；b为长期趋势；c为加法模型的季节因子，t表示样本取值时间，t+k表示将要预测的时期.a,b,c3个系数大小通过以下推倒公式来确定：

(7)

其中，α，β，γ是3个平滑因子；s表示周期长短.

学者们在研究该方法时提出了许多有关α，β，γ的参数空间选择的方法，本文要求所有的参数从区间[0，1]中选取.

2.2 模型确立

由于降水量序列没有长期趋势，有季节效应.故可用Holt-Winters季节加法模型进行预测.

运用公式(4)、公式(5)，利用2000—2018年昆明市月降水量的数据，可以得到模型结果如下式

(8)

2.3 模型检验分析模型确立

利用软件进行分析，Holt-Winters季节加法模型Box-Ljung检验结果9.

表2 Holt-Winters加法模型模型统计

结果显示Box-Ljung(18)=14.555，P=0.484，P>0.05，故通过白噪声检验，说明预测较准确.对残差序列进行统计学分析，拟合模型显著有效[12].通过预测值与真实值对比见图3，图中X为降水量的实际值，XF为预测值.可以看出该模型拟合较好.

图3 预测值与真实值对比图

3 两种模型预测结果对比分析

采取2种模型对2019年1—12月昆明市月降水量进行预测，并于实际降水量数据进行对比.预测结果显示：

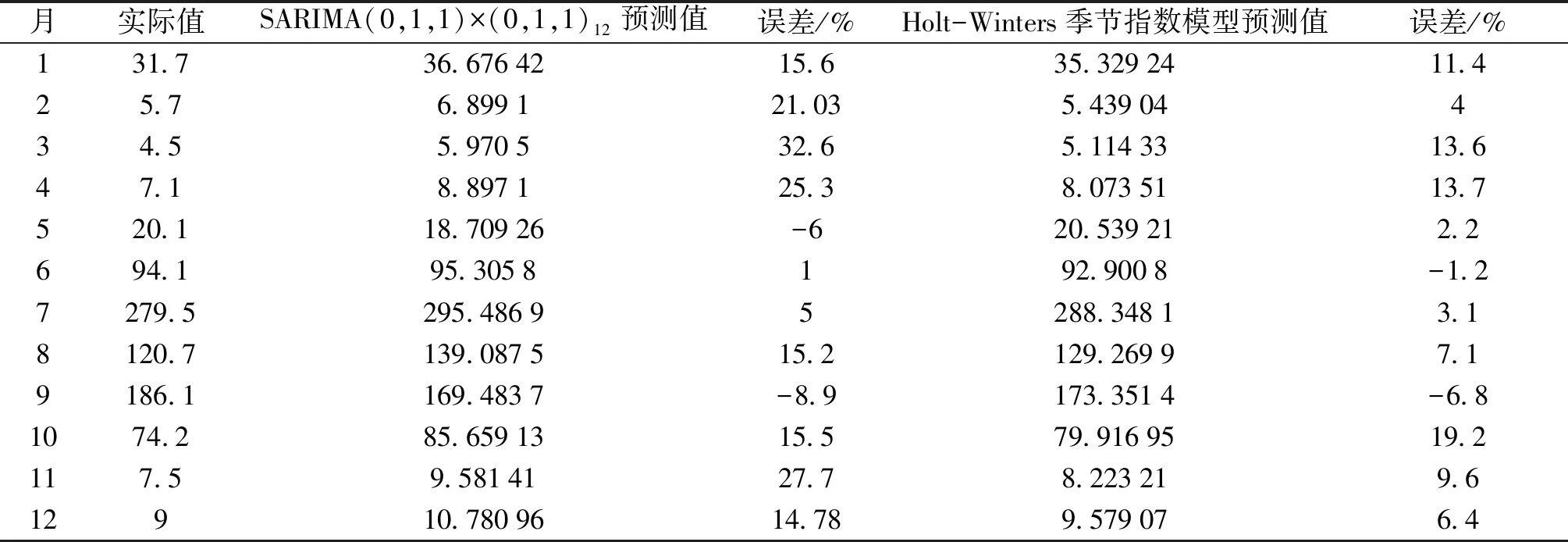
表3 2种模型预测结果对比

在本文中发现，在针对昆明市月降水量序列的预测建模过程中，通过误差比较Holt-Winters相加模型对实际数据的拟合效果优于ARIMA模型.

4 基于Holt-Winters相加模型预测2020—2022年降水量

使用Holt-Winters相加模型基于2000—2019年昆明市月降水量数据，对2020—2022年降水量进行预测.

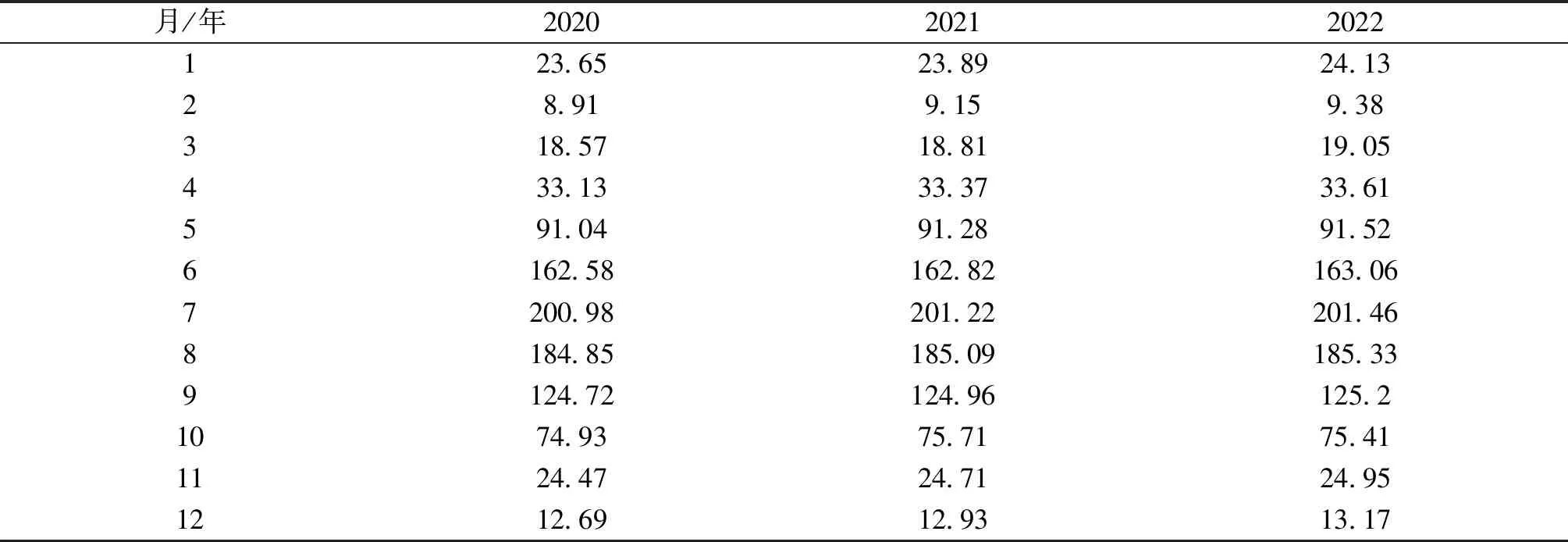
表4 2020-2022年预测结果

从预测结果可以看出3年降水量预测结果具有季节周期性波动，与往期数据相类似.且在7、8月降水量达到最高，1月和12月降水量最低，农业、水利等有关部门就可以及时采取防涝抗旱措施.

5 结语

昆明市月降水量会随季节周期性波动，SARIMA模型是针对平稳时间序列进行拟合预测模型，综合考虑了时间序列的趋势、季节效应、随机误差干扰等因素，可以更好的反应原始序列的趋势和变化.Holt-Winters相加模型则是根据数据在时间线上距离的远近依次给予不同权重，近期数据影响较大则赋予更大的权重，远期数据影响较小而被赋予较小权重，适合预测随时间变化趋势单一的数据[6].ARIMA模型和Holt-Winters模型都属于短期预测模型，它们的预测效果会随着时间的推移逐渐变差.从2种方法的预测结果中得出，短期预测效果都较好.本文中在针对昆明市月降水量序列的预测建模过程中，Holt-Winters相加模型对实际数据的拟合效果优于SARIMA模型.通过预测结果，可以使农业、水利等有关部门及时采取措施，防止旱涝灾害，降低不必要的损失.