基于K-SVD的低频水声信号去噪处理方法

吴耀文 ，邢传玺，张东玉，谢李祥

(云南民族大学 电气信息工程学院，云南 昆明 650500)

声信号在实现众多水下科研活动中都起着至关重要的作用，因为无线电波和光波等其他类型的信号无法很好地在水下传播[1].无线电波因其频率较高，在水中传播的过程中往往会导致其迅速衰减.光波在水中尤其是浑浊的水中穿透距离有限，衰减较快，一般在水下的传播距离为数十米左右.而声信号在水下具有良好的传输效果，尤其是低频声信号.低频声信号具有传播距离长，衰减慢和在水下的损耗小等特点[2]，这些方面受到了研究人员越来越多的关注.此外，水下目标的检测和定位、水声通信、数据传输等实际应用都需要准确的水声信号，这意味着由水声传感器接收到的信号需要具有较高的信噪比.但由于浅海环境复杂且多变，水声信号在传播过程中受到“2个 1 000”的约束，即“干扰强度是目标的一千倍、干扰数量是目标的一千倍”[3].因此接收到的水声信号往往混有各种各样的海洋噪声，其中噪声包括海浪、下雨、风暴、船舶以及海洋动物等.且低频水声信号更容易受到这些噪声的干扰，很大程度上影响了目标检测、定位与识别的准确性和有效性.

为了去除混在接收信号中的海洋噪声，提高接收信号信噪比，越来越多的研究人员使用稀疏分解(sparse decomposition)理论来对信号去噪进行研究.稀疏分解理论最早是由法国科学家Mallat等在1990年代提出的[4]，其原理是将从过完备原子库(overcomplete dictionary)中选择少数原子进行线性组合，即以较少的信息表示信号的特征.在稀疏分解理论中，过完备原子库也叫做过完备字典，其设计非常重要.学者们基于信号的先验信息构造了具有信号特性的过完备原子库.其中，孙同晶等[5]根据水声入射信号与回波模型的先验信息构造符合信号特性的过完备原子库，从而精确重构出水声回波信号.李扬[6]等根据大功率半导体激光器中的噪声模型成功构造出含有1/f噪声的过完备原子库，从而将信号中的该类噪声去除.这种过完备原子库构造方法的优点是其中的原子具有某类信号的特征，从而可以更好地将信号稀疏表示并得到较好的去噪效果.但缺点在于，原子库中的原子仅具有某类信号的特征，在对其他类型信号进行稀疏表示时会导致出现不令人满意的结果.鉴于此，研究人员展开了对训练字典的研究与运用[7-8].训练字典中的典型算法包括最优方向法[9](method of optimal directions，MOD)和K-奇异值分解[10](K-singular value decomposition，K-SVD)算法.其中，弓震等[11]运用K-SVD对实际的微地震信号进行去噪，仿真与实验结果显示，K-SVD算法对于地震信号具有较好的去噪效果.何天远[12]等根据压缩感知(compressed sensing，CS)理论，将K-SVD算法引入到对振动信号的重构中，实验结果表明，与其他方法相比，该方法具有更好的重构效果.史丽丽等[13]使用K-SVD算法对DCT字典进行训练更新，对不同信噪比的水声信号进行降噪处理，结果显示单频信号在信噪比较低时也具有较好的降噪效果，但没有对线性调频信号(linear frequency modulation，LFM)进行研究.

针对上述问题，本文将字典学习算法K-SVD引入到对水声信号的去噪处理中，有效减少原子个数，并通过仿真分别对不同海况下的简正波信号与LFM信号进行去噪处理.仿真结果表明，本文方法对不同海况且不同形式的水声信号都具有较好的去噪效果，信噪比增益可达到20 dB.

1 基本理论分析

根据简正波理论来建立水声传播模型，其中去噪方法为基于稀疏分解理论的正交匹配追踪算法(orthogonal matching pursuit，OMP)和K-SVD算法.其中OMP算法是一种信号稀疏表示方法，该方法可以在过完备原子库中选择少量具有信号的特征原子将信号稀疏表示，从而得到信号的有用分量；K-SVD算法是一种字典学习算法，基于当前字典的稀疏系数，通过迭代交替更新字典中的每个原子，直到达到最优解.

1.1 简正波理论

目前，计算声场的方法有很多，包括射线追踪、抛物方程方法、快速场程序、多径扩展技术和简正波理论等[14].通过简正波理论可以准确细致地描述声场，而且特别适用于浅海、低频和远场问题[15].简正波解可以通过距离函数Rl(r)和特征函数ψl(z)的乘积来表示，如下式所示

(1)

其中r为水听器到声源的距离，z表示水听器所处位置的深度.将上式带入声压方程可得简正波的特征方程

(2)

其中，k(z)=2π/λ表示波数，λ为波长.最后，浅海声场声压的简正波可以通过求解格林函数得到

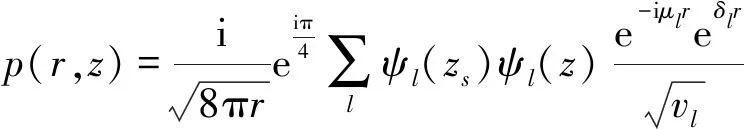
(3)

其中，vl=kr+iδl为简正波的复本征值；kr表示水平波数，δi<0为简正波的衰减系数.本文根据上式所示的传播模型进行仿真，获取波形预报[16].

1.2 稀疏分解理论

稀疏分解理论最早是由法国科学家Mallat等早在上世纪90年代提出的[4]，在信号处理和图像去噪方面得到较为广泛的应用[17].常用的稀疏分解算法有匹配追踪算法(matching pursuit，MP)、正交匹配追踪算法OMP以及它们的变体形式.其原理是将从过完备原子库中选择的少数原子线性组合，即以较少的信息表示信号的特征，可用公式表示如下

(4)

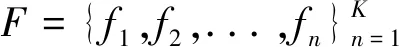
其中MP算法的原子选择过程如下：首先从过完备原子库D∈RN×M中选出与输入的N维信号矩阵F最匹配的原子d0，即信号与原子之间内积的最大值，使其满足

|[F,d0]|=sup|[F,di]|,

(5)

其中|[F,d0]|表示信号矩阵F与原子d0的内积，d0为第一次寻找到的最优原子.此时，信号F可表示为

F=[F,d0]d0+R1F,

(6)

式中[F,d0]d0是信号矩阵F在最匹配原子上d0的投影，R1F是信号矩阵F首次分解后的残差信号.然后对残差信号重复式(5)与式(6)的过程，即

RkF=[RkF,dk]+Rk+1F.

(7)

对信号矩阵F进行多次分解后信号可表示为

(8)

上式表明信号矩阵F可由分解K次后所选原子的线性组合与分解残差之和表示.在分解过程中，由于迭代次数的增长，残差信号的值会接近于零，所以最后的信号矩阵F可表示为

(9)

OMP算法所用原子选择方法与MP算法基本相同，其不同之处在于：对所选的全部最优原子，在分解过程中进行Schmidt正交化处理，选择过的原子不会再次使用，这使得在重构精度要求相同的条件下，OMP算法具有更快的收敛速度[18].OMP算法的稀疏表示过程如图1所示.

稀疏表示的目的是通过稀疏解析过完备字典上的信号，以较少的系数更完整地描述信号[19].当基于稀疏表示理论对含噪信号进行分解时，将残差近似视为噪声，然后用过完备字典和相应的稀疏表示系数重构信号，将其视为去噪后的有用信号.这使得运用稀疏表示来对信号进行去噪成为可能.

1.3 K-SVD算法

作为稀疏分解模型的基本组成部分，过完备字典的设计是非常重要的问题.一个合适的过完备字典可以增加稀疏表示的稀疏性，并且可以在各种应用中实现更好的表示.采用训练字典来对信号进行稀疏表示，不需要知道信号的先验信息，对于任意信号都可以自适应的对其训练匹配，直到误差达到指定阈值时即可得到最优解.本文在没有先验信息的条件下随机生成DCT字典，并加入字典学习算法K-SVD对字典中的原子进行训练更新.因为训练字典中加入了监督学习的过程，所以其中原子的个数大大减少，降低了算法的计算复杂度.

K-SVD算法是由Elad等[10]在2006年提出的一种字典学习算法，该方法是K-means算法的变形，主要运用了聚类的思想.在每次循环更新字典中的一个原子和对应的稀疏系数，在更新一个原子时，其它原子固定不变，在循环结束后，字典中的所有原子与相对应的稀疏系数同时得到更新.

K-SVD算法的主要思想可以通过求解以下模型的最小化问题来描述

(10)

其中X为稀疏系数矩阵，T0为信号的稀疏度，即稀疏系数中非零元的个数.(10)式是一个带有约束的优化问题，可以采用拉格朗日乘子法将其转化为如下形式

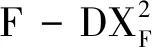
(11)

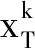
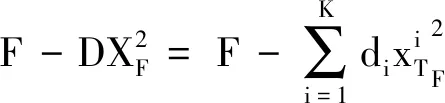
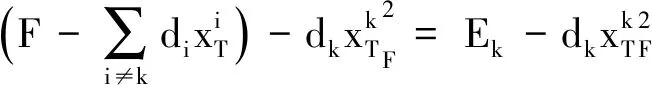
(12)

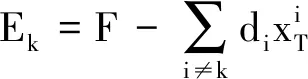
(13)

(13)式所示的优化问题可以通过奇异值分解(singular value decomposition，SVD)来进行求解.

2 去噪处理计算

本文去噪算法流程如图2所示.首先随机构造DCT字典D，然后使用OMP算法求得稀疏系数矩阵X，之后根据稀疏系数矩阵X与训练样本F对字典进行循环更新，当误差达到指定值时退出循环，得到训练后的字典D′，最后在新字典D′的基础上再次使用OMP算法得到新的稀疏系数矩阵X′，根据(4)式得到去噪后的重构信号Y′.

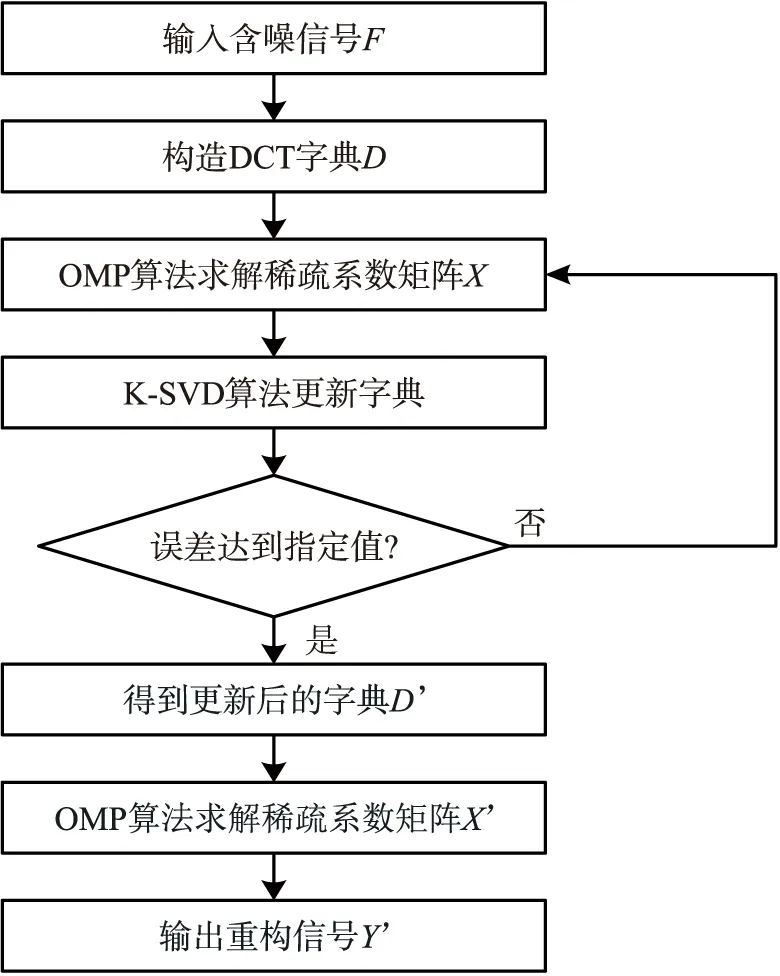
图2 去噪算法流程图

本文所用的去噪算法为OMP算法和K-SVD算法.具体实验步骤如下：

根据简正波方程即公式(3)进行波形预报，获取时域波形，得到仿真水声信号.

(14)

(15)

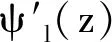
根据模拟的真实海洋环境在仿真水声信号中加入海洋噪声得到含噪信号F.

字典构造：使用离散余弦变换构造完备DCT字典D，如下式所示：

(16)

稀疏表示：使用OMP算法求解字典中每个原子di的稀疏系数xi，并得到稀疏系数矩阵X.

(17)

信号重构：在新字典D′的基础上再次使用OMP算法对含噪信号进行稀疏表示，得到新的稀疏系数矩阵X′，运用下式得到最终去噪后的重构信号Y′.

Y′=D′X′.

(18)

3 仿真结果分析

为验证本文方法的可行性和有效性，对不同海况下即不同信噪比的仿真低频水声信号进行去噪处理，验证该方法的去噪效果。基于2013年在黄海实验的真实海洋环境数据进行仿真，首先根据简正波方程即公式(3)进行波形预报，发送信号频率为500Hz，采样频率为1kHz，仿真简正波信号及频谱如图3所示。为验证该方法对于不同形式信号的去噪效果，我们对频率位于200～400Hz之间的线性调频信号进行仿真，其时域波形与频谱如图4所示。根据被动声纳方程，假设声源可全方位接收，声源级为120dB，接收指向性指数为0。表1为根据文献[20]得到的不同海况与不同频率下的浅海噪声级数。

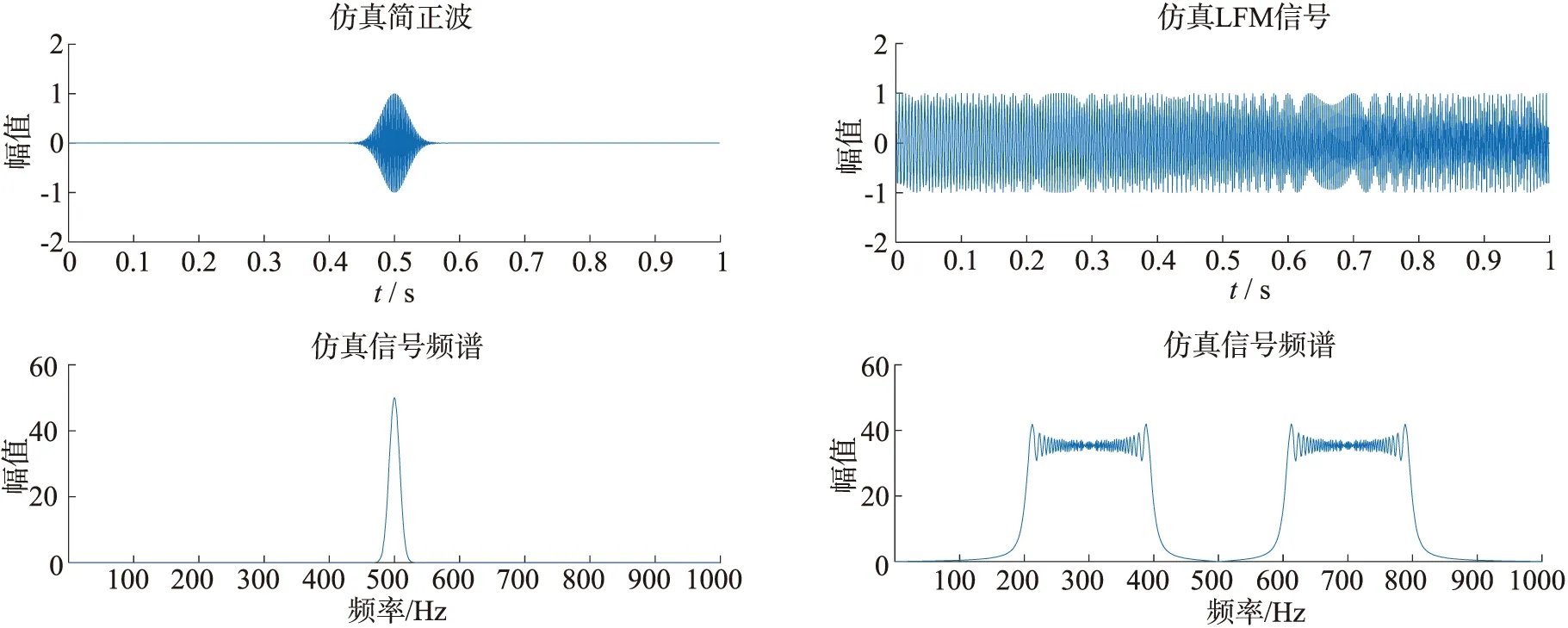
图3 仿真简正波及频谱 图4 仿真LFM信号及频谱

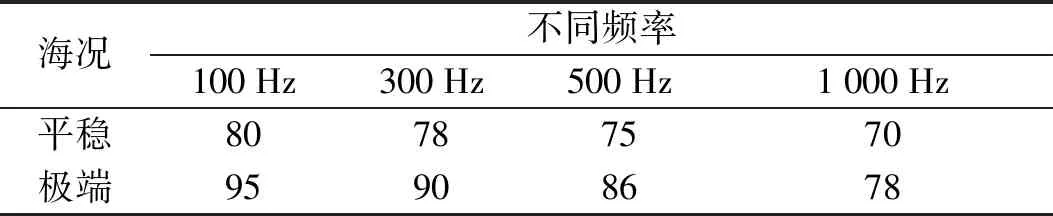
表1 浅海噪声级数 (dB)

根据被动声纳方程，假设声源与水听器间的传播损失为 40 dB，并根据表1中不同海况时的浅海噪声级数计算可得，在平稳海况下且信号频率为 500 Hz 时的接收信号信噪比约为 5 dB。在极端海况条件下接收信号信噪比为 -6 dB.

实验参数设置如下：DCT字典行数与信号长度N相等为 1 000，根据文献[21]，如果采用传统稀疏分解算法时过完备字典中的原子个数应设置为52 (Nlog2N)，约为 518 284 个，因本文采用训练字典，所以原子个数不必远远大于信号长度，可缩短程序运行时间，这里设置为信号长度的2倍即 2 000；稀疏度选择10，误差为1×10-6，在此条件下循环100次后观测结果.

图5和图6分别显示了仿真简正波在平稳海况与极端海况下的去噪结果.从图5(a)中可以看出，在平稳海况下，接收到的信号被噪声干扰，时域波形出现毛刺现象.如图5(b)所示，经过本文方法去噪后，时域波形变得更加平滑，重构信号信噪比为 25.07 dB.从图6(a)中可以看出，在极端海况下，接收到的信号时域波形已经完全被噪声淹没，看不出有用信息.如图6(b)所示，在经过本文方法去噪后，可以明显看到时域波形，且频域波形更加平滑，重构信号信噪比为 13.73 dB.仿真结果表明本文方法对于单频简正波信号有较好的去噪效果，在2种海况下的信号信噪比增益均可达到 20 dB 左右.

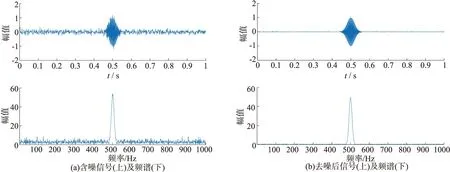
图5 平稳海况下对仿真简正波的去噪结果

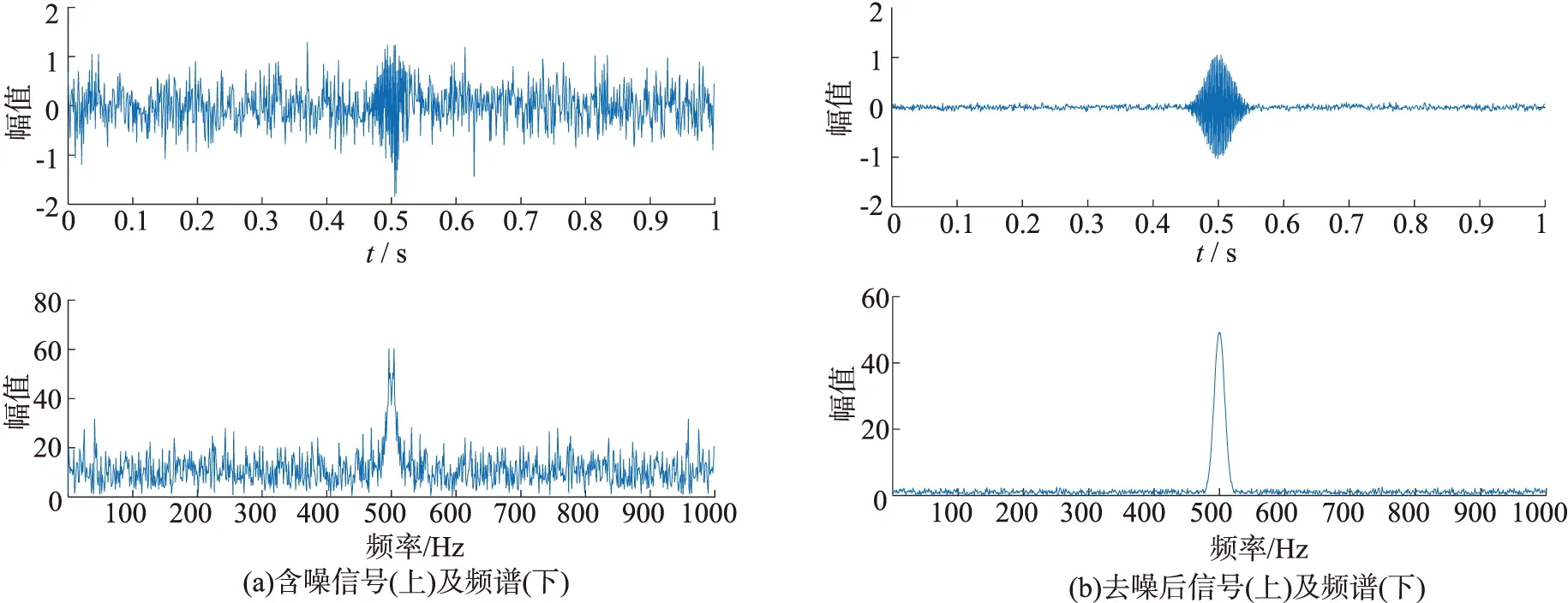
图6 极端海况下对仿真简正波的去噪结果

图7和图8分别显示了仿真LFM信号在平稳海况与极端海况下的去噪结果.从图7中可以看出，在平稳海况下，接收信号的时域和频域波形因噪声而变得模糊.经过本文方法去噪后，时域与频域波形更加平滑，重构信号信噪比为 25.29 dB.从图8中可以看出，在极端海况下，接收信号的时域与频域波形均被噪声完全淹没.经过本文方法处理后，可以看到噪声得到明显地去除，重构信号信噪比为 13.62 dB，且从频谱图中可以看出信号频率在 200 ～400 Hz 之间，符合实验预期结果.

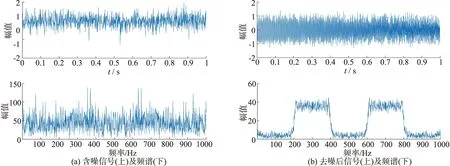
图8 极端海况下对仿真LFM的去噪结果

为验证本文方法在极低信噪比下的去噪效果，将接收信号信噪比设为 -20 dB，并在相同的仿真环境下对其进行去噪处理，结果如图9所示.从图 8(a)中可知，在极端海况下还可以看出接收信号的频率为 500 Hz，但在图9(a)中已经完全看不出接收信号的频率信息.在经过本文方法去噪后的信号时、频域图像如图9(b)所示，可以明显看出去噪后重构信号的时域波形，且信号频率为 500 Hz，证明本文方法在极低信噪比下对噪声同样具有较好的抑制效果.

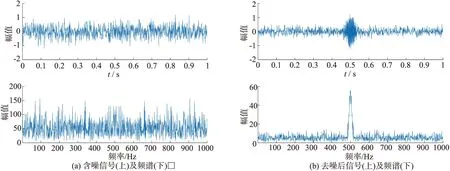
图9 极低信噪比下对仿真简正波的去噪结果

4 结语

针对复杂多变的海洋环境，为更好地去除海洋噪声对接收信号的干扰，本文将字典学习算法引入到水声信号的处理过程中.并通过仿真对不同海况下的简正波信号与线性调频信号进行去噪处理，仿真结果表明，该方法在低信噪比的条件下对不同形式的信号都有较好的去噪效果.同时对极低信噪比下(SNR=-20 dB)的接收信号进行去噪处理，发现信噪比增益均可达到 20 dB.