吸声系数的传递函数法仿真计算

2021-09-09漆琼芳罗建军

声学技术 2021年4期

张苗，漆琼芳，罗建军

(1. 武汉第二船舶设计研究所，湖北武汉 430060；2. 渤海造船厂集团有限公司，辽宁葫芦岛 125004)

0 引言

吸声材料广泛应用于建筑、船舶、车辆等的吸声处理中，吸声系数是材料的一项重要声学性能指标，目前测试样品的吸声性能测试主要有阻抗管法和混响室法，阻抗管法认为波是垂直入射的，依据双传声器的传递函数可得到吸声材料的吸声系数、反射系数、声阻抗、声导纳，且需要的试件少。混响室法认为入射波是无规则分布，需借助于混响室且所需试件面积较大[1]。传递函数是系统输入与输出间的固有特性，测量两个传声器的复声压，根据传声器间距、传声器与试件的间距，计算传声器之间的复传递函数，得到试件的法向入射吸声系数[2]。

目前，范丹丹[3]设计了阻抗管结构、采集系统、扬声器等，形成了一套完整的阻抗管样机系统，通过理论和试验方法验证了样机的可行性，通过样机测试了海绵、聚氨酯、木头、鸡蛋棉等吸声材料的吸声系数，为常用吸声材料的选择提供了一定依据。朱有剑等[4]基于传递函数的理论研究设计了一套阻抗管，测量海绵的吸声系数，将设计的阻抗管测试结果与传统驻波比法进行比较，验证了所开发系统的准确性，通过对比试验提出了测量吸声系数时的操作注意事项。梁小光[5]通过改变材料孔隙率、流阻等计算吸声系数，认为硅酸盐基多孔材料存在最佳的流阻和孔隙率。

本文基于Virtual.lab Acoustics建立阻抗管和试件的声学模型，建立声源及传声器位置处场点，计算吸声材料阻抗，提取传声器测点处的复声压，基于传声器间距、传声器与试件距离，得到传声器测点处的传递函数，并计算得到试件吸声系数。将本文计算结果与文献值[6]进行对比，验证了阻抗管模拟方法及传递函数计算的有效性。探讨了阻抗管直径、传声器测点位置对吸声系数的影响。对阻抗管内试件后侧空气柱、安装倾斜角度、试件厚度等试件安装状态进行定量参数分析。

1 管道声传播及传递函数法

管道内声传播的波动方程[7]为

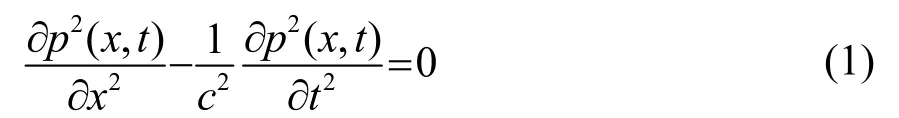
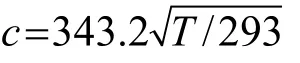
以图1所示实验用阻抗管为例，阻抗管的试件管一端安装试件，发声管一端布置有模拟扬声器的平面波声源，测量靠近试件的两个传声器的声压，根据传声器间距及与试件距离关系，可求得两个传声器间的传递函数。

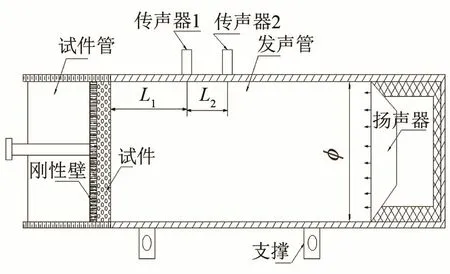
图1 阻抗管示意图Fig.1 Schematic diagram of impedance tube

式中：ρ为阻抗管内空气密度，c为阻抗管内声速。

2 吸声系数声学计算模型

2.1 阻抗管模型的建立

建立阻抗管的空气层、试件的三维模型并划分网格，将网格导入LMS Virtual.Lab Acoustics商业软件，进行声学网格前处理，建立传声器场点。实验条件下的声源是扬声器，已知阻抗管内扬声器可以产生平面波和非平面波，非平面波在大于3倍管径的位置会衰减，因此在施加平面波声学模拟扬声器时，声源离传声器距离至少为3倍管径[2]，为覆盖吸声系数的测试频段100～6 300 Hz，使用以下3种阻抗管：

本算例以质点振动模拟平面波声源，得到传声器测点1和传声器测点2的振速如图2所示，经过式(16)计算得到相应的声压，经过式(2)～(15)进行数据后处理计算，得到吸声系数。

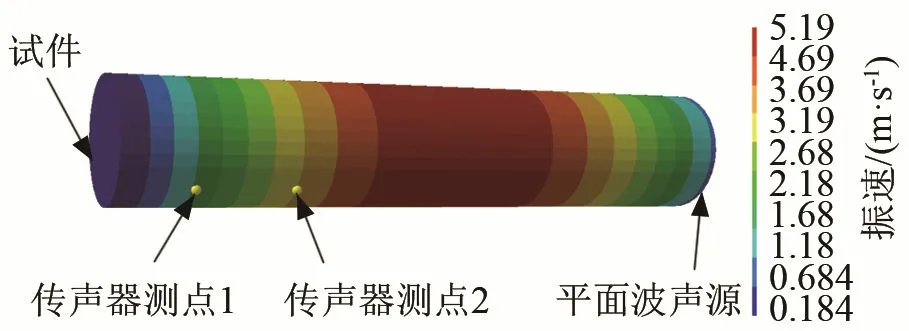
图2 直径100 mm阻抗管的振速云图Fig.2 Vibrating velocity nephogram in φ 100 mm impedance tube

2.2 模型有限性验证

为了验证本声学计算模型和传递函数后处理编制计算程序的有效性，采用文献[3]中的算例，大管直径100mm，传声器与试件最近距离L1=50mm，传声器间距L2=80mm，计算频率范围500～2 500Hz，步长为20 Hz，毛毡厚度20mm，空气密度为1.225 kg·m-3，声速为340 m·s-1，毛毡流阻为23 150 Pa.s·m-2，孔隙率为0.93，结构因子为1，网格尺寸为10 mm，得到的吸声系数曲线与文献Delany-Bazley-Miki公式[6]的对比情况如图3所示，可知两者结果吻合较好，证明了本阻抗管声学模型及边界条件施加的有效性，验证了传声器测点复声压并求取传声器之间的传递函数的有效性，也验证基于LMS Virtual.Lab Acoustics平台导出测点复声压、根据传递函数后处理计算吸声系数是可行的。

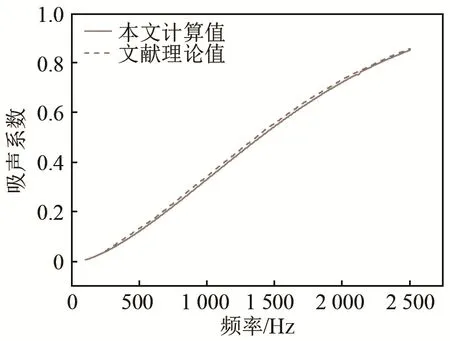
图3 计算值与文献[6]公式计算值对比Fig.3 Comparisons between calculated values in this paper and in literature[6]

2.3 模型分频段

根据实验用三种阻抗管类型，将传声器测点的复声压导出，按照公式计算出试件的吸声系数，计算频率范围100～6 200 Hz，步长20 Hz，得到的吸声系数曲线如图4所示。图4中大管100(50-80)代表模拟的直径10 mm大阻抗管，传声器与试件最近距离L1=50 mm，传声器间距L2=80 mm。在3 900 Hz以上，小管模拟的吸声系数比大管大，按照试验用阻抗管分频段计算，在重叠频率采用求平均值插值后再拟合的方法，最终合成的吸声系数曲线，按照以上原则，在频段交界处拟合，得到最终试件的吸声系数。

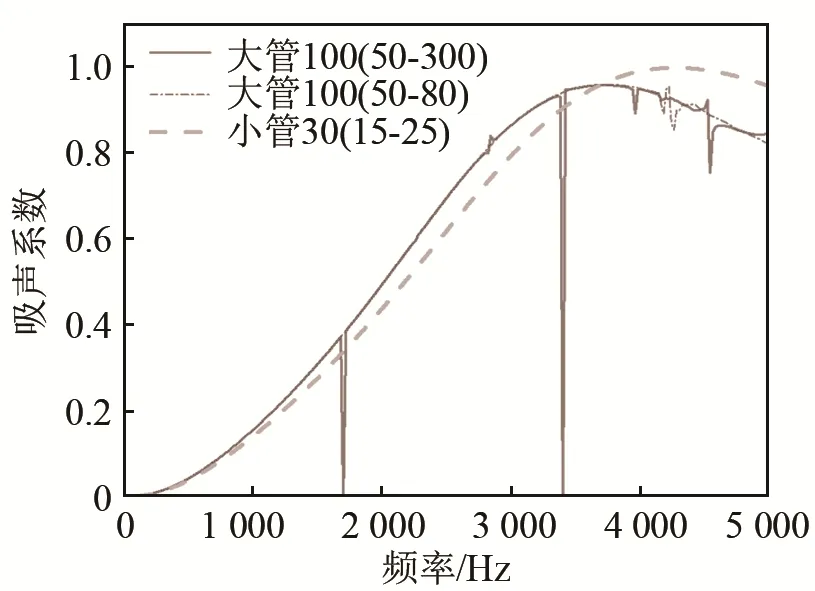
图4 三种阻抗管计算的吸声系数曲线Fig.4 Sound absorption coefficient curves of three types of impedance tubes

传声器布置位置对吸声系数计算的影响如图5所示。由图5可知，以测试用直径为100 mm的大阻抗管为模型，当传声器位置不同时，分析频带为100～6 300 Hz。试验室用大管(50-80)(代表L1=50 mm，2L=80 mm，其余类推)可测试400～1 600 Hz频段而不出现试件阻抗率畸变，大管(50-300)在测试125～500 Hz频段内仿真模拟的阻抗管，在该频段内均没有低谷，不会出现试件阻抗率畸变。所以实验室用阻抗管采用大管(50-80)的传声器测点布置有其合理性，而大管(50-170)和大管(50-300)出现了几个明显的低谷，存在声阻抗率畸变。

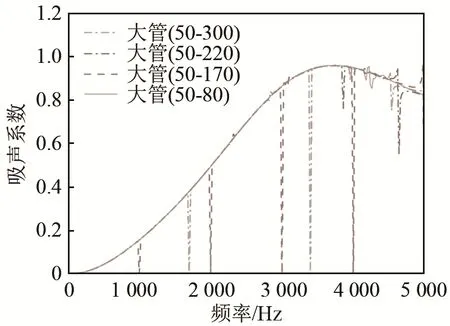
图5 传声器布置位置对吸声系数计算的影响Fig.5 The influence of microphone location on the calculation of sound absorption coefficient

根据曲线低谷捕捉可知，大管100(50-300)在1 660、3 360、5 060、5 660 Hz时吸声系数均有极小值出现，大管100(50-170)在960、1 960、2 960、3 960、4 960、5 960 Hz时均有吸声系数曲线极小值出现，可能与管内声模态有关，对直径100 mm大管进行声模态计算，模态频率如表1所示，在1 960 Hz左右出现峰值，声模态云图如图6所示。两种情况下传声器测点处于声压云图较接近部位，采用阻抗管法仿真计算吸声系数时，传声器测点对声阻抗率影响较大，可能引起噪声吸声系数曲线位置的选择畸变。

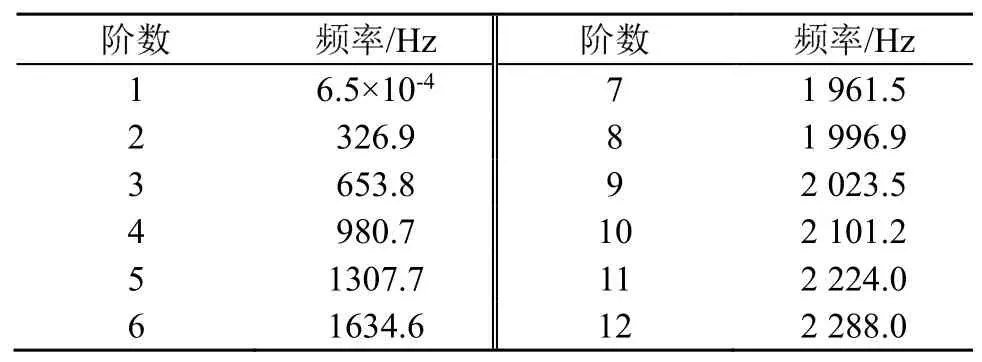
表1 阻抗管内声模态Table 1 Acoustic modes in impedance tubes

图6 直径100 m大管的声模态云图Fig.6 Sound modal nephogram in φ 100 mm tube

3 试件安装状态对吸声系数的影响

阻抗管测试规范[2]对试件的安装提出了适当要求，可通过仿真探讨试件安装状态对吸声系数的影响，阻抗管安装参数主要包括试件后侧与刚性壁是否紧贴、试件厚度是否均匀、试件安装是否平整等。

3.1 试件后侧空气层厚度

模拟大阻抗管：管径φ=100 mm，施加厚9 mm的文献[3]用吸声材料，传声器位置L1=50 mm，传声器位置L2=80 mm，当试件管的刚性壁与试件管内的间距分别为紧密接触(0 mm空气层)、10 mm厚空气层、20 mm厚空气层、30 mm厚空气层时，仿真得到传声器测点的复声压，将导出结果进行传递函数后处理，得到的试件吸声系数曲线如图7所示。

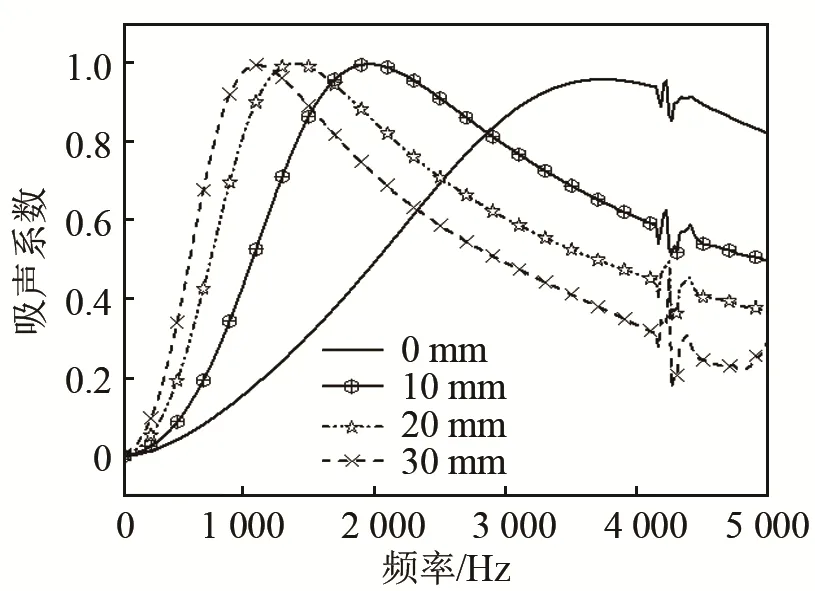
图7 试件后侧空气层厚度对吸声系数的影响Fig.7 The influence of the rear air layer thickness of the specimen on the sound absorption coefficient

根据试件后侧空气层模拟可知，试件在安装时后侧的空气层厚度对吸声系数有明显影响，随着空气层厚度的增加，吸声系数曲线向低频移动。在进行阻抗管试验时，试件与后侧刚性壁应安装紧密，避免出现空气层。

3.2 试件厚度对吸声系数影响

模拟大阻抗管：管径φ=100 mm，施加文献[3]用吸声材料，传声器位置L1=50mm，传声器位置L2=80 mm。当试件厚度分别为4、9、19、29mm时，吸声材料厚度对吸声系数的影响如图8所示。

由图8可知，在一定厚度范围内，随着试件厚度的增加，吸声系数曲线有向低频移动的趋势。

图8 试件厚度对吸声系数的影响Fig.8 Effect of specimen thickness on sound absorption coefficient

3.3 试件倾斜度对吸声系数影响

假设试件在安装时不平整有角度倾斜，则大管100(50-80)在试件平整和试件法向有 5°倾斜的安装状态下，计算的吸声系数曲线如图9所示，试件一定角度的偏转使吸声系数曲线呈现无规则状态。综合如图10所示的声压云图可知这种无规则状态与靠近试件的传声器1的声场处于非平面波状态有关，在阻抗管设计时，传声器1与试件应适当隔开一定距离，以确保传声器1和传声器2均处于平面波声场中，且传声器1和传声器2应避开使计算出的声阻抗率产生畸变的位置。