基于全聚焦算法的骨折超声成像研究

宋小军，张 璠，黄 琼，曾俊冬,3

(1. 上海电力大学电子与信息工程学院，上海 200090；2. 复旦大学电子工程系，上海 200433；3. 上海大学机电工程与自动化学院，上海 200444)

0 引 言

临床经验表明，长骨骨折主要发生在股骨、肱骨、胫骨和腓骨处。根据骨折状况可分为横断、斜切、螺旋、蝶形四类[1]。本文主要研究类型为长骨的简单横断性骨折。长骨骨折的诊断常使用磁共振成像(Magnetic Resonance Imaging, MRI)和电子计算机断层扫描(Computed Tomography, CT)等技术[2]。MRI利用磁共振现象从骨骼中获取电磁信号，重建出长骨骨折信息，有分辨率高、对比度大等优势，但是有扫描速度慢、设备操作复杂、适用人群受限等缺点；医院常见的CT扫描在人体胫骨质量评价方面有着长足发展和应用，但是CT设备昂贵，检测过程有电离辐射，对患者健康有一定负面影响。超声无损检测发明早期就应用于医学领域，有着设备简单易操作、无辐射、扫描速度快等优点，但是由于人体骨骼系统各向异性复杂，回波信号质量差，传统超声检测(如B超检测)在骨折诊断方面应用受限。

超声检测在骨折检测方面应用近年来成为热点。Chen等[3]分别用X射线和超声扫查兔下颌骨，用斯皮尔曼等级相关分析(Spearman’s correlation coefficient for ranked data)对比了两种方法成像结果，得出超声检查可以代替X射线检查的结论，为超声诊断与传统医学检查之间的对比、评价分析提供新方法。马振兴[4]使用超声波检测离体牛股骨，验证了超声波评价骨愈合状况的可行性。Li等[5]、Liu 等[6]使用二维时域有限差分法(Two Dimensional Finite Difference Time Domain, 2D-FDTD)研究A0、S0导波在不同宽度和角度的骨折裂缝中振幅变化规律，为定量评价骨折状况提供理论依据。Zhang等[7]使用BC和OBC编码激励提高超声回波信号的幅值，改善了成像信噪比，结果表明被优化的超声有评价长骨骨折深度的潜力。许凯亮等[8]采用混合边界元方法(Hybrid Boundary Element Method,HBEM)对超声导波在骨裂长骨中的传播情况以及各导波模式的反射系数和透射系数进行了数值分析，为选择最优入射导波模式和频率，更好地定量评价骨质以及骨裂状况提供依据。

骨超声成像方面，罗春苟等[9]介绍了宽带超声衰减(Broadband Ultrasonic Attenuation, BUA)成像和超声传导速度(Speed Of Sound, SOS)成像两种松质骨超声参量成像方法的基本原理和应用情况，提出了发展超声背散射系数成像，以简化骨超声成像的实验过程、提高成像精度；黄凯[10]分析出了超声背散射信号中的三种参数，分别将参数值映射为像素值成像，对松质骨进行诊断；文献[11-12]为重建皮质骨骨折图像，使用多静态合成孔径超声(Multistatic Synthetic Aperture Ultrasound, MSAU)抑制图像伪影，提高了超声成像对比度噪声比，清楚地显示了皮质骨骨折情况；Renaud等[13]假设胫骨由群速度不同的多层均匀质层组成，利用射线追踪法计算不同介质间的超声传播路径，从而完成皮质骨超声成像。Dixon等[14]为研究快速临床骨折诊断方法，提出3D超声成像法，超声成像结果与常规2D-X射线图像对比后，得出3D超声成像可以对长骨骨折有效检测的结论；Tang等[15]使用超声弹性成像法，对兔股骨骨折成像，结论表明超声弹性成像技术可用于准确识别长骨中骨折的存在和位置。

本文提出利用全聚焦算法(Total Focusing Method, TFM)对骨折进行超声成像，从而为骨折的临床检查提供其他的方法。全聚焦算法是基于全矩阵数据后处理的一种虚拟聚焦超声成像算法，可以实现成像区域任意点虚拟聚焦[16]，具有解决长骨超声成像分辨率低、缺陷精度差等问题的潜力。

本文建立软组织-牛胫骨板离体双层介质超声检测模型。在Field II仿真验证单层介质全聚焦成像的可行性基础上，分别利用传统单层介质全聚焦和双层介质折射点修正全聚焦算法对牛胫骨进行成像，对比分析两种算法在缺陷宽度、软组织和骨板厚度三种实验参数的相对误差，验证双层介质全聚焦成像在骨折超声检测中的可行性。

1 全聚焦成像算法原理

1.1 全矩阵数据采集

全矩阵数据是指将超声相控阵换能器内所有阵元依次作为发射-接收阵元组合，所采集到的超声回波时域信号，是发射阵元序列、接收阵元序列和时间采样点数的三维数据[17]。

N个阵元的超声相控阵采集全矩阵数据采集示意图方法如图1所示。首先激发第一个阵元，所有阵元同时接收回波，由第一个发射阵元和接收阵元组成的发射/接收对记录的回波数据记为S1j，其中j=1 ,2, …,N；然后依次激发剩余阵元，重复上述接收过程，回波数据记为Sij，i=1 ,2, … ,N，i表示发射阵元，j表示接收阵元，采集结束后Sij组成全矩阵数据集如图2所示，共N×N组数据。

图1 全矩阵采集示意图Fig.1 Schematic diagram of full matrix capture

图2 全矩阵数据集Fig.2 Full matrix capture data

整个数据采集过程收集成像区域的所有信息，其中包括缺陷信号。TFM是基于全矩阵数据的时域后处理的成像算法，因此全矩阵数据采集(Full Matrix Capture, FMC)是TFM能够对全部成像区域虚拟聚焦的基础。

回波信号和标准发射信号互相关计算可以在一定程度上减少噪声含量[18]，因此进行全聚焦成像之前对回波信号进行互相关计算处理。

1.2 传统单层介质全聚焦成像算法

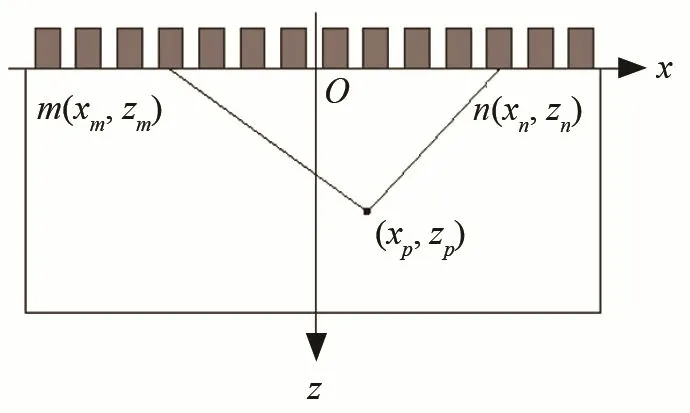
图3 传统全聚焦成像模型Fig.3 Imaging model of traditional total focusing method

1.3 折射点修正后的双层介质全聚焦成像算法

根据三角函数关系和已知量即可分别求出B、B’的横坐标[19]。

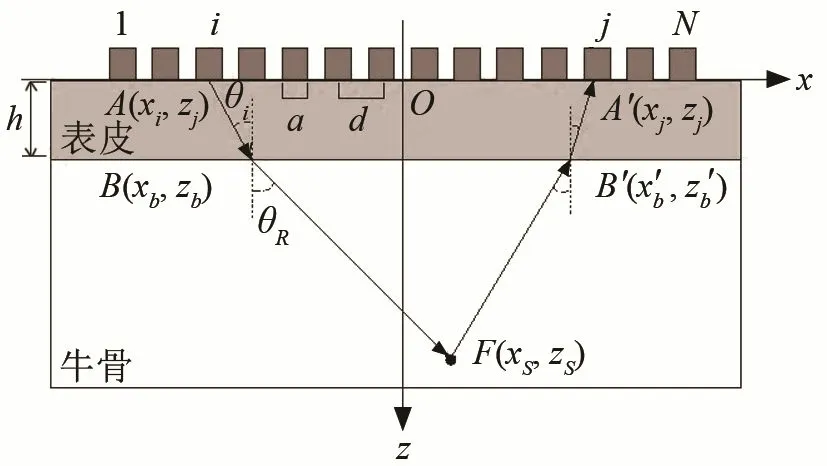
图4 折射点修正后的双层介质全聚焦成像模型Fig.4 Imaging model of the total focusing method of doublelayer media after refraction point modification

2 仿真及离体骨板实验

2.1 Field Ⅱ仿真实验

使用Field II建立仿真模型。如图5所示，阵列排列方向为x轴，垂直阵列方向为z轴，均匀固体材料中有一处贯通横向裂纹，裂纹深度h1=4 mm，宽度设置w=2.50～5.00 mm，声速c=3 000 m·s-1。仿真设置采用32探头线性相控阵，位于材料表面上方。

图5 Field Ⅱ仿真固体材料裂纹模型Fig.5 The Field Ⅱ simulated crack model of solid materials

仿真采用的超声相控阵参数如下：换能器中心频率f0=6.25 MHz，采样频率fs=25 MHz，阵元间距a=0.30 mm，阵元宽度等于波长(c/f0)，阵元高度h2=5.00 mm。正弦激励脉冲参数如下：振幅A=1，角频率ω= 2πf0，初相φ0= 0。

2.2 离体骨板实验

实验采用离体牛胫骨骨板作为实验材料，实验装置示意图如图6(a)所示，采用Verasonics系统(Vantage 128 or 256, Verasonics Inc, WA, USA)进行测量，探头型号为L11-4V，128通道，阵元间距为0.30 mm，中心频率为6.25 MHz，采样频率为25 MHz。骨板长为90.00 mm，宽为30.00 mm，厚为5.00 mm，分别在四组骨板样本中间制作宽度为1.00～4.00 mm的贯通间隙模拟骨折状况。

为了更好地模拟在体实验，用厚度为2.00 mm的动物表皮软组织贴合在骨板上面。在骨板和软组织中的声速分别为3 000 m·s-1和1 540 m·s-1。

如图6(b)所示，发射信号为脉冲信号，AL为脉冲信号的幅值。Verasonics系统控制阵元依次发射脉冲，每次发射时所有128阵元都进行接收，数据经总线传输到计算机储存。

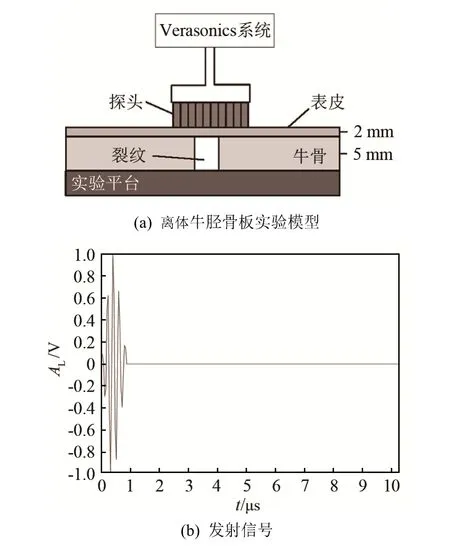
图6 实验设置和检测用的发射信号Fig.6 Experimental setup and the emitting signal for detection

3 实验结果与讨论

3.1 Filed II仿真结果与分析

将全矩阵数据进行全聚焦成像处理，图7为仿真成像结果，AN为归一化幅度。图7(a)为一组发射-接收对的回波信号，在5 μs附近可观察到一次反射回波，对应固体材料表面的反射波。图7(b)为全聚焦算法处理后的成像结果。固体材料仿真模型中的裂纹宽度为4.00 mm，成像结果中裂纹宽度为4.30 mm，相对误差为7.50%。

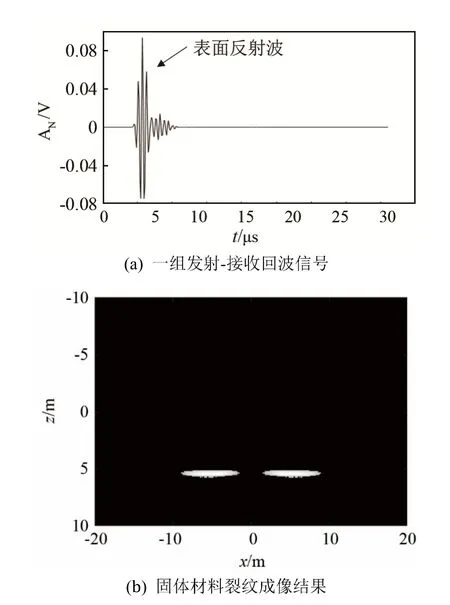
图7 固体材料裂纹仿真结果Fig.7 Simulated result of cracks in solid materials

为验证全聚焦成像的准确性，对不同宽度裂纹的固体材料进行仿真。Field Ⅱ仿真实验裂纹宽度成像结果如表1所示，裂纹成像结果的平均相对误差为5.60%。

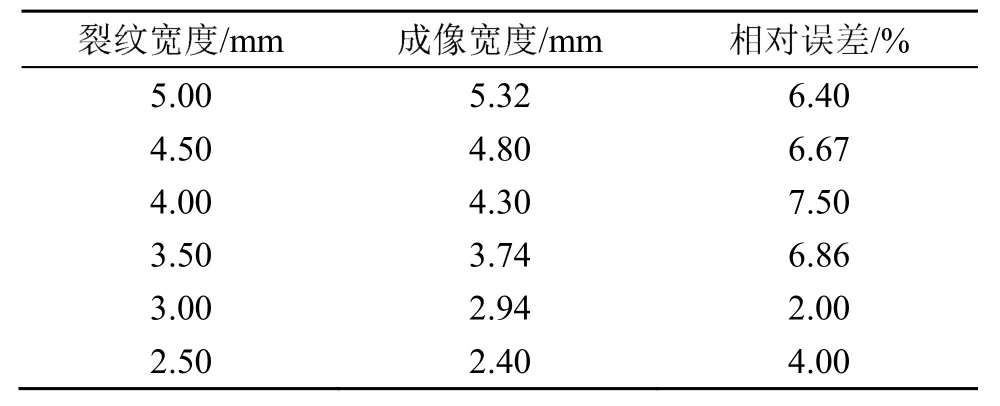
表1 Filed Ⅱ仿真裂纹宽度及相对误差Table 1 FiledⅡsimulated crack width and relative error

3.2 离体牛胫骨板实验结果与分析

图8为采用TFM算法对一组牛胫骨板样本全矩阵数据集进行成像的结果。图8(a)为5发1收的回波信号。在2.5 μs和5 μs附近可观察到两次反射回波，分别对应软组织和牛骨板上表面的交界面以及骨板下表面。由于超声在骨板中的衰减，第二次回波的幅度比第一次回波小很多。第三次回波为多次反射波，是超声波在骨板里多次反射形成的。

图8(b)为5发1收的回波信号与标准发射信号互相关结果。从图8(b)可见，通过互相关计算可以显著地提高信噪比。

图8(c)为传统单层介质TFM算法处理后的成像结果。从图8(c)可以清晰地看出软组织与骨板交界面和骨板下底面。交界面位于z=1.90 mm附近，即软组织厚度为1.90 mm，与实验设置厚度基本一致，相对误差为5.00%；骨板底面在z=5.00 mm处，骨板厚度为3.00 mm，相对误差为40.00%，与实验骨板厚度相比误差较大，这是没有考虑声波在软组织与骨板交界面的折射，声波传播路径分析存在偏差和传播时间计算错误导致的结果；骨折间隙宽度为2.75 mm，相对误差为8.33%。从成像误差来看，单层介质全聚焦成像具有较好的骨折间隙宽度估计和软组织厚度估计能力。考虑到在体实验很难直接测量软组织厚度，单层全聚焦成像结果可以为双层介质TFM提供必需的软组织厚度先验信息。

图8(d)为经过折射点修正的双层介质TFM算法处理后的成像结果。从图8(d)可以看出，软组织与骨板的交界面位于2.15 mm附近，即软组织厚度为2.15 mm，相对误差为7.50%；骨板底面在z=7.10 mm附近，即骨板厚度为5.10 mm，相对误差为2.00%；骨折间隙宽度为2.80 mm，相对误差为6.67%。骨折间隙宽度结果表明折射点修正后的双层介质TFM算法，对牛胫骨骨折状况有较为准确的成像结果。

四组牛胫骨实验骨折间隙宽度成像结果如表2所示，间隙宽度平均相对误差为6.98%。测得的骨板平均厚度为4.96 mm，平均相对误差为5.75%，方差为0.345 mm2。此外，测得的软组织平均厚度为2.04 mm。由此可见，本文提出的方法能实现骨板间隙成像，也可以对软组织厚度、骨板厚度进行较为准确的评估。

表2 多组骨板实验中双层介质TFM成像的骨板间隙宽度及相对误差Table 2 The crack widths and relative errors of bone plates imaged by double-layer media TFM in four groups of experiments

从图8(d)可以明显看出伪像、伪影，一方面原因是软组织厚度较薄，使得被检骨板处于换能器近场范围内，声波信号受到近场干扰；另一方面，为提高骨板下底面的信号强度和成像效果，在信号处理过程中使用算法缩小了第一次回波与第二次回波的幅值差异，同时也相对放大了噪声的幅值。以上两种原因都会导致伪像、伪影出现。为消除近场干扰，可以在探头与实验对象间添加人工表皮垫。人工表皮垫厚度为5.00 cm，密度为1.016 g·cm-3，声速为1 540m·s-1，声阻抗为1.59×105g·cm-2·s-1，其主要声学属性与软组织一致，不会影响声波传播。后续计算中计入表皮垫厚度的影响，可得出正确的成像结果。对于噪声干扰，作者在后续研究中，将从信号滤波预处理和图像优化两个方向继续探究消除伪像、伪影的方法，以改善成像效果。

4 结 论

为了探索新型、安全、便携的骨折诊断方法，本文分别采用传统单层介质全聚焦成像和折射点修正后的双层介质全聚焦成像算法，对Filed-Ⅱ仿真和牛胫骨板离体实验的全矩阵数据集进行成像显示。仿真实验的裂纹宽度平均相对误差为5.60%，表明全聚焦成像可以有效检出单一介质的裂纹缺陷；离体牛胫骨板实验中，通过传统全聚焦算法成像，能将骨折间隙宽度和软组织-骨板交界面准确呈现，相对误差分别为8.33%、5.00%；骨板厚度相对误差为40.00%，即传统全聚焦算法很难准确呈现骨板下底面；利用修正折射点后的双层介质全聚焦成像，改变了声波传播路径和延时法则，不仅能将骨折间隙宽度和分界面显示，平均相对误差至6.98%；还能把骨板下底面较为准确地成像，骨板厚度平均相对误差降低为5.75%。因此基于全聚焦成像的骨折超声检测在临床应用上有较好的发展潜力。