G2.5超声波燃气表的仿真与实验研究

王舒文，李中阳，金文胜，陈维厅，徐晓丹，赵伟国

(1. 中国计量大学，浙江杭州 310018；2. 浙江苍南仪表集团股份有限公司，浙江温州 325800)

0 引 言

燃气作为国家重要的绿色能源，是国家和城市基础设施的重要组成部分。燃气表是计量燃气流量的重要工具，是衡量整体用气量的重要仪器，在整个燃气供应产业链中拥有无可替代的地位。目前市场上的主流燃气表为传统的膜式燃气表，该测量原理为容积式流量测量方法，存在具有可动部件、压损大、生产装配复杂、人力成本较大等缺点。超声波流量测量方法与传统容积式流量测量方法相比，具有准确度高、重复性好、无可动部件、压损小等优点，已经广泛应用于一些高压、大流量计量领域[1-3]。

在家用燃气测量领域中我国起步较晚，2015年制定发布了《超声波燃气表》(CJ/T 477——2015)，2016年启动编制国家标准[4]。在国外，超声波燃气表已经普遍使用在德国、意大利、日本。在超声波传感器安装、声道设计方面，多声道组合可以提高流场适应性，不同换能器位置会影响流场，不同流速剖面偏差不同[5]；对于时差法超声流量测量电路及信号处理方法已进行深入研究[6]。信号处理方面最新的研究方法有动态阈值调整法[7]、相关法[8]等。但是由于燃气压力小、流量变化大、流速低，现有的信号处理较难解决小流量测量，导致的超声波测量精度低的问题。

针对以上问题，本文从流道仿真入手，设计了两种不同的超声燃气基表，并对两种模型进行数值仿真计算，以解决超声波在燃气流量测量中的小流量问题。通过仿真提取管道内超声波传播路径的数据，建立基于此区域规则分布的离散点的集合，通过对所有离散点的速度进行相关计算得出结果，从而反映整体区域流场速度的大小和分布的均匀性，得出更为合理的模型。最后通过流量实验，验证数值仿真计算的结果。

1 时差法测量原理

时差法是一种基于声学技术的测量方法。当介质流动与超声波传播同向时，超声波传播速度随介质流动速度的增加而增加；当介质流动与超声波传播逆向时，超声波传播速度随介质流动速度的增加而减小。进而可以根据超声波顺流和逆流传播时间求取时间差，从而获得流体的流速信息，测量模型如图1所示。

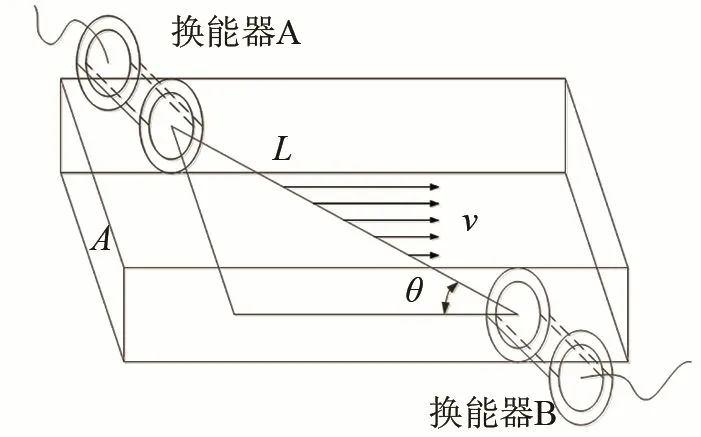
图1 超声波流速测量模型Fig.1 The ultrasonic flow speed measurement model

如图1中所示，顺、逆流的传播时间TAB、TBA分别为：

其中：C为介质静止时的声速，θ为声道角，v为流速，L为超声波传播距离。则时差ΔT为

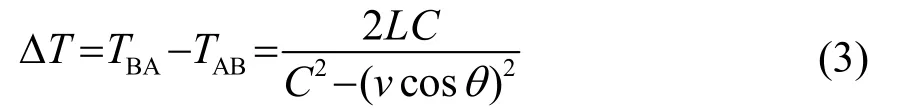
常温常压下，空气的声速C为340 m·s-1，存在C≫vc osθ，则式(3)可写为

因此可求得流速v为

则可以求得体积流量q的公式为：

其中：A为管道的横截面积。

2 模型设计与仿真计算

2.1 管道模型设计

本文采用一种在空腔中放置超声波测量流道的结构，设计了扁平管路增加分流片的测量流道，根据放置方式的不同，设计了两种管道后径角度不同的固定装置(模型1为90°，模型2为180°)，如图2、图3所示。

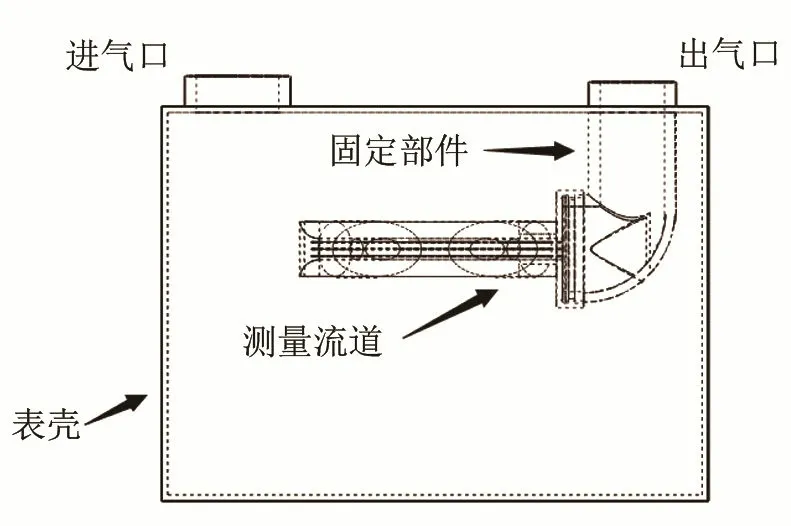
图2 管道模型1剖面图Fig.2 Sectional drawing of the pipeline model 1

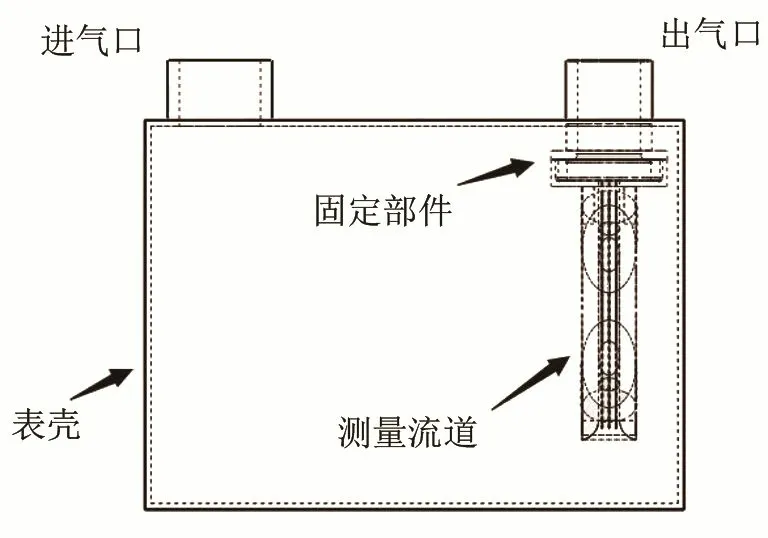
图3 管道模型2剖面图Fig.3 Sectional drawing of the pipeline model 2

传统的圆形管道内，超声波流场与测量性能的影响关系已经被广泛分析研究，得出了很多经典的理论[9-10]，但是对于非圆形管道内气体流场的分析却并不多见。同时，已有研究者提出了采用方形的测量管路[11]。在拥有相同直径的情况下，方形管道的面积要远小于圆形管道。当体积流量q一致时，管道截面积A越小，流体流速v越大，即流速的分辨率越大。同理，在流体速度v越大的情况下，得到的顺逆流时差ΔT也越大，即时差的分辨率越大。时差的分辨率越大，测量的精度就越高。所以，本文在确定外部腔体结构尺寸和换能器尺寸的情况下，采用并设计了方形管道，管道剖面图如图4所示，具体尺寸如图5所示。

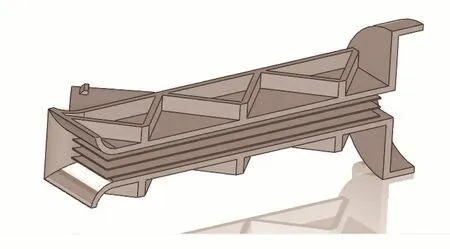
图4 方形管道剖面图Fig.4 Sectional drawing of a square pipeline

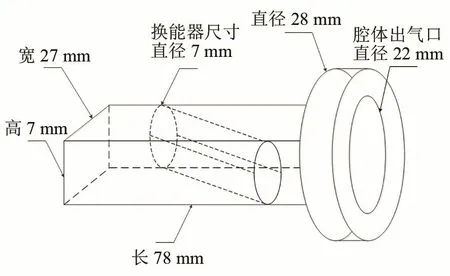
图5 超声波测量流道尺寸图Fig.5 Dimensional drawing of ultrasonic measuring-pipeline

此外，在测量流道中加装一定数量的整流板，作用一：整流板一定程度上可以抑制流场中的扰流情况；作用二：流道的横向管径相对减少，在相同流量的情况下，流经流道中的气体流速更快，得到的时差更大，则得到的流量点的精度更高[12]。但是，整流板数量越多，会阻碍超声波在路径上的传播。本文在前期准备中，对同一基表在加装不同数量整流板的情况下，比对接收回波信号的强度(信号峰峰值)、零点信噪比、管道压损等指标进行测试，比较结果如表1所示。由表1中可以看出，当整流板的数量从2变化到4时，零点信噪比接近一致。但是，在整流器数量从3变化到4时，管路压损继续增大，回波峰峰值下降明显。考虑尽量增加整流板数量的情况，选择整流板数量为3时，信号的信噪比变化不大，回波峰峰值与整流板数量为2时接近，而且压损与燃气表检定规程要求的压损上限(200 Pa)有一定的余度，因此选择整流板的数量为3。

表1 不同数量整流板指标比较Table 1 Experimental data for different numbers of rectifier boards

通过SOLIDWORKS软件对两种模型进行建模，然后导入ICEM CFD软件绘制网格。在做过网格数量无关性实验之后，最终两种模型的网格数在4×105～5×105之间。

2.2 初始条件确定

本文采用计算流体动力学(Computational Fluid Dynamics, CFD)方法分析两种管道模型在不同流量点下的流场速度分布[13]，利用Fluent软件进行相关仿真。

本文设计的超声燃气表为G2.5型，根据超声波燃气表检定规程[14]，其最小检测流量点qmin为0.025 m3·h-1，分界流量点qt为0.4 m3·h-1，最大流量点qmax为4 m3·h-1。因此，本文选取此三个流量点来进行仿真。

依据本文管道尺寸计算，管道中的流速最大不超过20 m·s-1，则其马赫数小于0.06，将气体流动视为恒定、不可压缩流体的流动。依据雷诺数计算公式，三个流量点在基表的入口速度分别为：0.011 2、0.18、1.80 m·s-1，其雷诺数分别为21、345、3450。因此在流量点qmin、qt，管道内流体状态表现为层流；在流量点qmax，流体状态表现为湍流。

为简化模型，假定气体为不可压缩流体，气体在管道内做定常运动。稳定的工况下，认为整个流动过程是等温过程。空气为黏性流体，黏性系数为1.789 4×10-5kg·s·m-1，密度为1.225 kg·m-3。环境温度设置为 20℃，进气口设置为速度入口(velocity-inlet)，出气口设置为压力出口(pressure-outlet)，压力设置为0。设置qmin和qt的求解模型为Laminar层流模型，qmax的求解模型为k-epsilon湍流模型。

2.3 结果分析

本文关注的重点流场区域是超声测量管道部分，因此提取速度云图中超声测量管道区域，同时超声测量管道内3块整流板将其分隔为Z1、Z2、Z3、Z4四部分。图6分别显示qmin流量点时对应的两个模型各四部分区域的截面速度云图；图7分别显示了qt流量点对应的两个模型各四部分区域的截面速度云图；图8分别显示了qmax流量点对应的两个模型各四部分区域的截面速度云图。

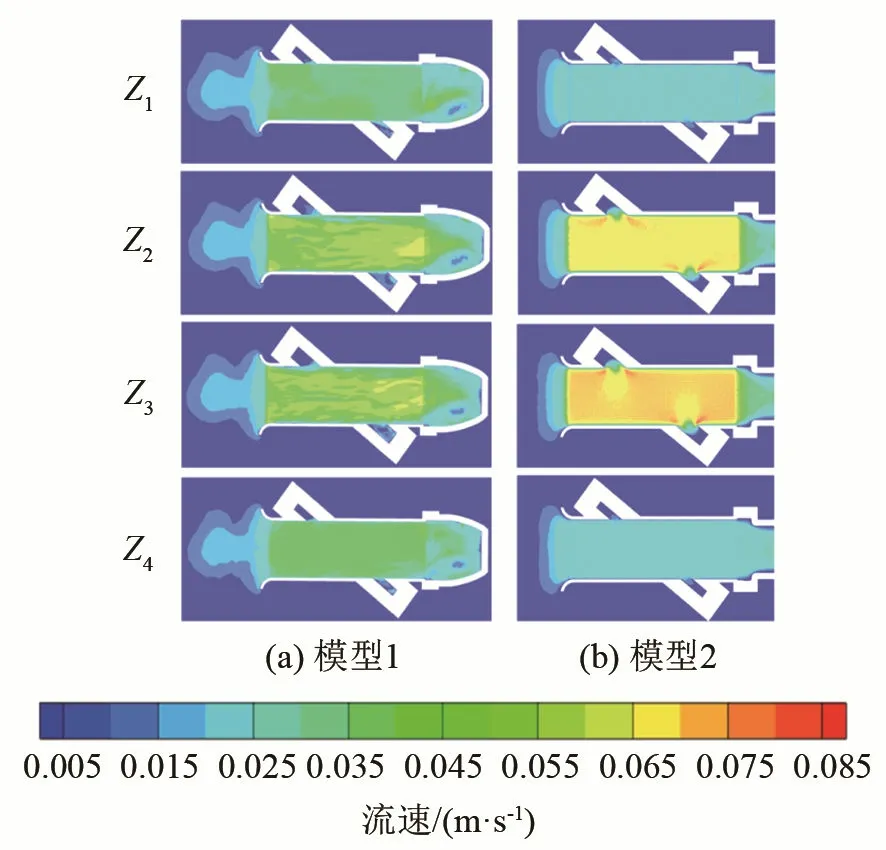
图6 超声测量管道区流量为qmin的截面的速度云图Fig.6 Velocity nephogram at the section of the flow of qmin in the ultrasonic-measuring pipeline

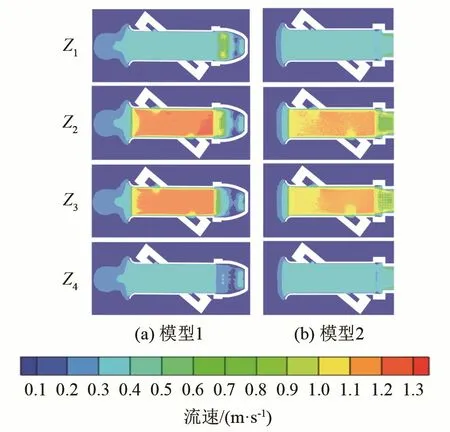
图7 超声测量管道区域流量为qt的截面的速度云图Fi g.7Velocity nephogramatthesectionofthe flowof qt in the ultrasonic-measuringpipeline

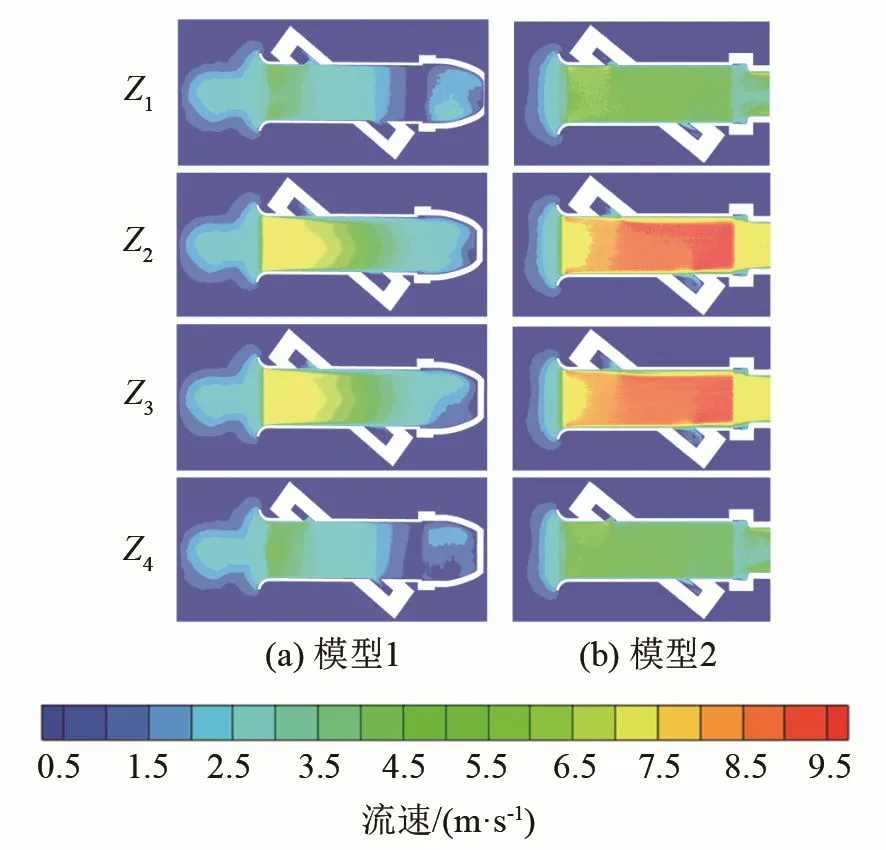
图8 超声测量管道区流量为qmax的截面的速度云图Fig.8 Velocity nephogram at the section of the flow of qmax in the ultrasonic-measuring pipeline

从速度云图中可以看出，中间两层的流场速度分布更集中、更剧烈。同时，在qmax流量点，模型1流场更集中在测量管道入口，而模型2更集中在测量管道内部。

为了进一步准确得到超声换能器传播区域的速度分布情况，将超声波换能器的传播测量区域进行提取，将提取的超声换能器传播区域进行划分，以超声波传播区域离散点的速度值为集合求取相对均方根，以便能够通过离散特征点的数据集合来反映整体超声波传播区域的速度分布特性。如图9所示为超声波换能器在管道内的测量区域，圆形传播测量区域被整流板分成四部分，取每部分流域的中间面为Z面，分别为Z1、Z2、Z3、Z4；将Z面均分为11份，取中间10个等分点，分别为X1、X2、....、X10；取Z面与每一传播测量区域的交界点以及两交界点的中心点，分别为Y1、Y2、Y3。按如图9所示进行划分，得到X、Y、Z三个面的特征点，如(X1，Y1，Z1)、(X1，Y1，Z2)等总计共120个特征点。

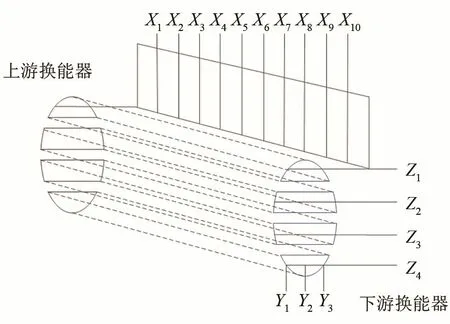
图9 超声波测量区域特征点示意图Fig.9 Schematic diagram of characteristic points in ultrasonic measuring area

采集所有特征点的速度数据并对该区域所有特征点的速度求相对均方根值，计算公式如式(7)：

为方便计算式(7)，引用标准差计算公式：

式(7)、(8)进行化简得到：

分别对两种模型在三个测试流量点下采集得到的速度值数据计算相对均方根，最后得到的结果如表2所示。同时提取三个流量点Z2、Z3层的速度大小数据，分别计算其速度均值，如表3所示。

从表2中可以得出，模型1在qmin和qt流量点的相对均方根值要小于模型2，在qmax流量点的相对均方根值要大于模型2；由表3可见，模型1在qmin和qmax流量点的速度均值要小于模型2，在qt流量点的速度均值要大于模型2。

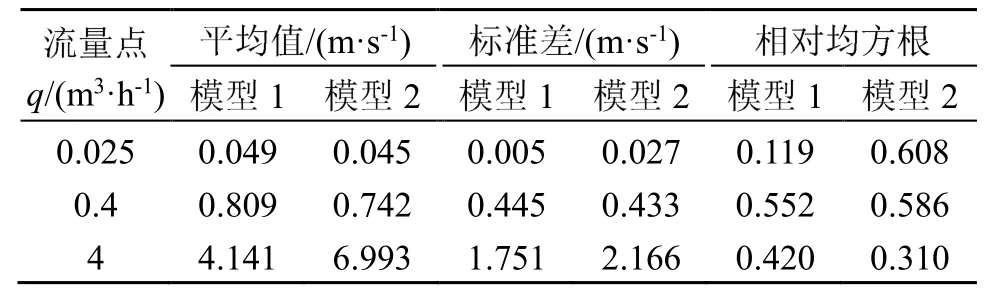
表2 两种模型特征点流速计算数据表Table 2 Calculation data of flow velocity at the characteristic points of two models

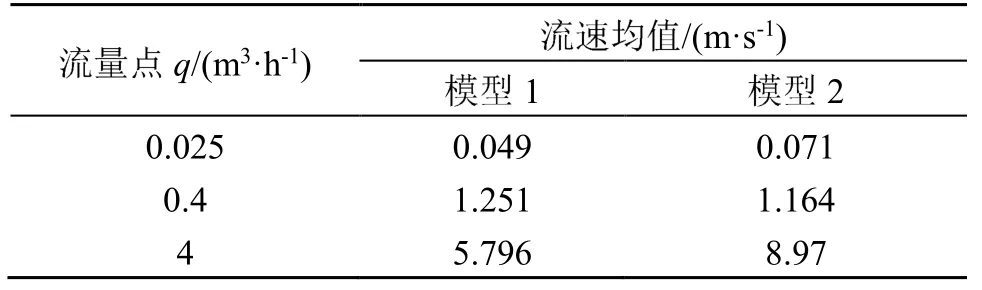
表3 两种模型的Z2、Z3层的流速均值数据Table 3 Mean velocities of two models at thelayers of Z2、Z3

在小流量测试领域，由于测量得到的传播时间非常小，相比于流场带来的速度分布均匀性的影响，依据时差法测量原理，同一流量点下，管道内流速越大，测得的时差越大，时差分辨率越大，更能够提高测量的准确性和稳定性，因此选择模型2为更合理的样机结构。

3 实验验证

3.1 流量检定装置

本次实验采用的是音速喷嘴气体流量标准检测装置，其测量精度为0.5级，装置简图如图10所示。该装置由离心泵、储气罐、汇流管、电磁阀、音速喷嘴、滞止容器、压力计和温度计组成。该标准装置使用负压法方式，采用真空装置在音速喷嘴下游抽取真空，形成音速喷嘴所需临界流条件，滞止压力为大气，流量稳定。实验测试使用的超声燃气表样机所图11所示，超声燃气表样机如图12所示。

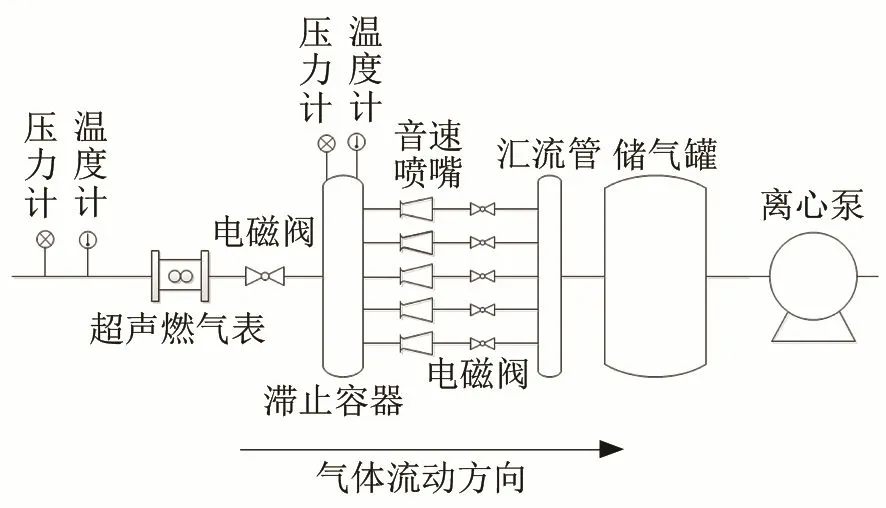
图10 标准流量检测装置示意图Fig.10 Schematic diagram of the standard flow detection device

图11 标准流量检测装置实图Fig.11 Picture of standard flow detection device

图12 超声燃气表样机Fig.12 Prototype picture of the ultrasound gas meter

标准装置通过几只不同流量值的喷嘴组合形成一系列流量点，下游的真空泵运转产生负压，气体流经被检表，进入滞止容器中，再经过音速喷嘴。流量大小也可以通过电磁阀阀门运转来控制，测量滞止容器中压力与温度以及被检表前的压力与温度，即可计算得到流过被检表的标准体积流量。

3.2 实验测试

本次实验在室内温度20℃、标准大气压下进行，在标准检测装置上对两种基表进行流量测试，每个仿真流量点分别测试三次，装置根据三次测量误差计算出实验重复性，记录重复性数据，两种模型的实验数据如表4所示。

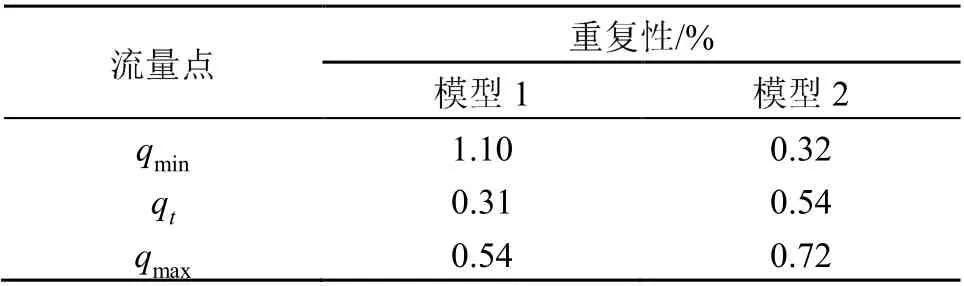
表4 两种模型实验数据表Table 4 Experimental data of two models

从表4中可以看出，在qmin流量点，模型2的重复性优于模型1；在qt和qmax流量点，模型1的重复性优于模型2，但结果基本一致。

由于超声燃气表在低压小流量测试范围的精度和稳定性更加难以控制，在实验数据上相差更大。因此本文在上述实验的基础上，针对小流量测试范围，从中选取0.025、0.04、0.08、0.15、0.25 m3·h-15 个流量测试点，对两种模型的测试性能继续比对，每个测试流量点分别测试三次，观察影响。实验结果如图13和图14所示。

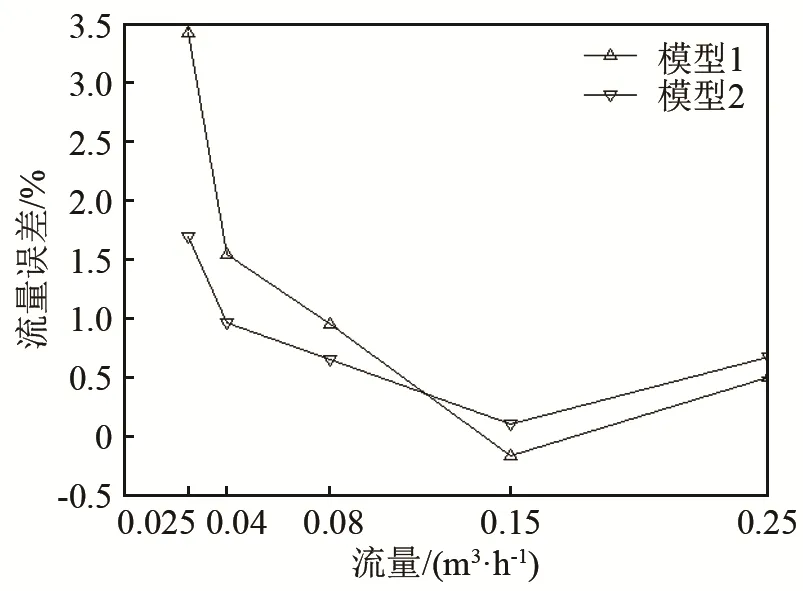
图13 对比实验误差均值数据Fig.13 Mean error data in comparison experiments

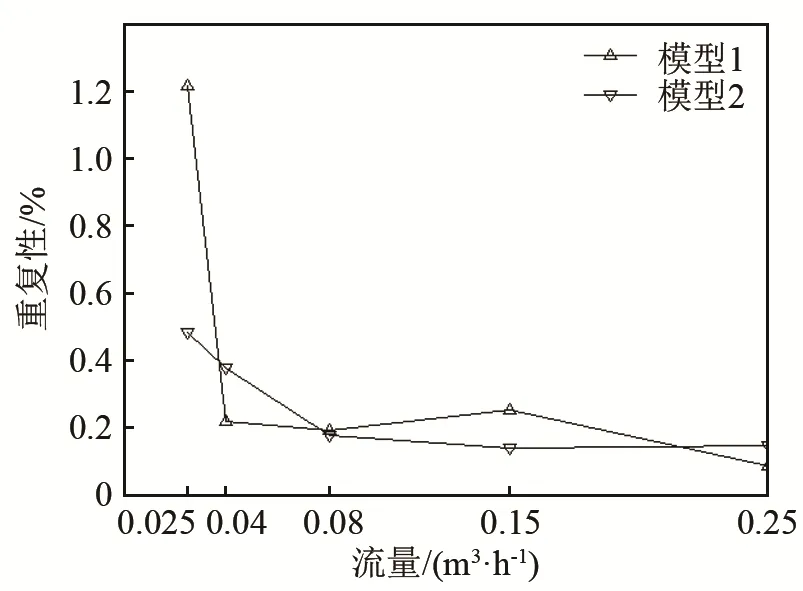
图14 对比实验重复性数据Fig.14 Repetitiveness data in comparative experiments

从图13和图14的数据中可以看出，模型2的测试结果，无论从测试误差均值的稳定性，还是误差的重复性方面都优于模型1，实验数据验证了流体仿真结果的正确性。

4 结 论

本文以流场适应性分析为出发点，设计了两种不同结构的基表模型。通过建立模型、绘制网格，进行数值仿真计算，获得两种模型在不同流量下的流场分布。建立了一种基于超声波传播区域的离散点集合，依据离散点速度数据计算区域速度的均值和相对均方根，分析整体区域流场速度的大小和分布均匀性，选取模型2作为样机模型，最后通过测量性能比对实验，验证了数值仿真计算的结果的正确性，并验证了竖直放置(后径角度为180°)的模型2是更合理的样机结构。