基于三角形折叠的牵引变电所BIM模型几何轻量化

徐 凯，陈小强，郑云水，王 英，常战宁

(1. 兰州交通大学 自动化与电气工程学院，兰州 730070；2. 中国铁路兰州局集团有限公司 供电处，兰州 730000)

2013年，中国铁路总公司将BIM技术作为未来铁路信息化发展主要方向[1].四电站后工程专业众多，牵引变电所内场景复杂，BIM模型精度要求高，搭建场站模型产生巨大数据量[2]，普通移动设备内存容量、总线带宽和处理能力不能满足对牵引变电所设备仿真模拟，限制BIM技术在四电工程虚拟仿真中的应用[3].以往都是通过大型移动工作站解决问题[4]，导致项目投入增大，降低了工程项目经济性.因此，铁路行业BIM模型轻量化问题亟待解决，需要在保持模型几何特征基础上减少数据量，实现较高的实时交互性能.

文献[5]提出一种基于三角形折叠简化算法，通过控制模型中点到平面距离误差达到模型轻量化目的，减少模型中三角形数量并保持拓扑结构.文献[6]提出一种基于网格划分三维模型轻量化算法，针对模型特征添加约束因子，减小模型轻量化误差，提高模型轻量化质量.文献[7]提出一种基于简单曲面检测的三维模型轻量化算法，将三维模型中曲面进行分类并进行参数化描述，达到轻量化目的.文献[8]提出一种基于二次误差测度的边界保持分级简化算法，顶点加入预定权重进行分级简化，保证渐进式简化过程，保留模型边界特征.文献[9]提出一种特征保持混合折叠算法，算法进行三角网格分类，实现特征区域和非特征区域分类处理.

对BIM模型进行轻量化处理主要分为几何元素轻量化处理与非几何元素轻量化处理.几何元素轻量化处理通过减少模型点、线、面来达到轻量化处理效果；非几何元素轻量化处理是指对BIM模型全生命周期信息进行无损压缩，达到信息轻量化目的.

基于此，引入针对BIM模型几何元素轻量化处理算法—改进二次误差测度算法(quadric error metrics,QEM)，在三角形折叠误差中加入邻接三角形平均面积、多邻域曲率、顶点重要度3个细节特征约束因子，优化误差矩阵，实现保持模型细节特征条件下模型轻量化处理.

1 基础研究

1.1 基本定义

1.1.1 模型定义

定义1：将包含设备设计数据、建造信息、维护信息等全生命周期信息的三维信息模型定义为BIM模型.

定义2：将模型尺寸、三角面数量、点数量和空间拓扑信息定义为BIM模型几何元素.

定义3：将模型名称、规格型号、材料材质、生产厂商、功能与性能技术参数，以及系统类型、施工方式、工程逻辑关系和设备运维信息等定义为非几何元素[3].

1.1.2 三角形定义

定义1：模型中，将具有公共边和公共顶点的三角形组成集合为三角形网格TM(triangle mesh)，三角形网格包含三角形集合T与三角形顶点集合V[5].

定义2：三角形网格TM中，若存在一条边没有邻接其他三角形，定义为边界边，其所在三角形定义为边界三角形；不满足该条件的三角形定义为内部三角形[5].

定义3：三角形网格TM中，所有与顶点vi0相关三角形组成集合定义为与顶点vi0相关三角形集合[5].

定义4：三角形网格TM中，所有与三角形Ti三个顶点相关三角形构成集合定义为与三角形Ti相关三角形集合[5].

1.2 三角形折叠原理

三维模型轻量化实质为三角形折叠，进行一次三角形折叠等同于两次边折叠，三角形折叠效率越高，折叠质量越高[10].三角形折叠是一种迭代几何元素删除方法，基本思想是将三角面作为删除元素，将三角形收缩为一个点.通过迭代减少三维模型中三角面数量来达到模型轻量化目的.图1为三角形折叠，将折叠前三角形Ti简化为折叠后点V.

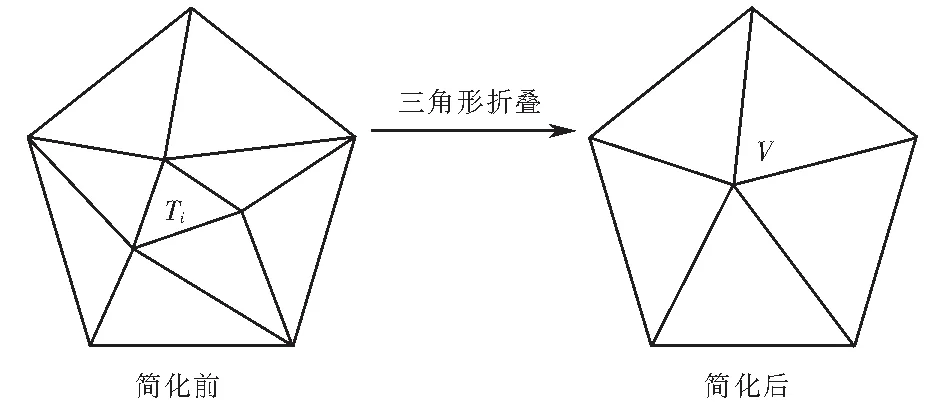
图1 三角形折叠Fig.1 Triangle folding

三角形折叠后效果好坏取决于折叠误差大小[11]，所以在折叠过程中确定使折叠误差最小最优，改善折叠效果.轻量化处理后三维模型不改变设备细节特征，需要选择折叠后新顶点vi0，新顶点vi0=[xi0yi0zi01]T位置的选择决定折叠误差大小.误差越小，轻量化处理前后模型越相似.为解决新顶点最优解问题，文献[5]使用二次误差测度算法进行折叠误差度量，每个三角形中，用一个4×4的矩阵来表示三角形误差矩阵Qi，则三角形折叠误差α(Ti)为

(1)

其中：vi0为新顶点位置；x、y、z为新顶点坐标；三角形误差矩阵Qi为

新顶点最优解是将折叠误差α(Ti)控制到最小.

(2)

若式(2)有解，则可求出新顶点位置vi0；若无解，则选择三角形中点、三角形三边中点或者三角形三个顶点作为新顶点，在给出7个点中，求出使式(1)值最小的点，将该点作为折叠后新顶点[12].

2 改进二次误差测度算法

牵引变电所设备三维模型复杂度高，建模要求精度高，涉及多种设备，设备模型间位置精度要求高，电缆线路走线复杂.针对以上特点，将邻接三角形平均面积、多邻域曲率、顶点重要度加入折叠误差计算中，找到适合牵引变电所设备模型轻量化方法.

2.1 二次误差测度算法

由Garland于1997年首次提出，算法以三角形为折叠对象，产生新顶点，将新顶点到相关三角形所在平面距离平方作为衡量误差的标准.使用QEM算法进行误差度量可得到高质量简化模型，同时具有简化效率高、占用内存小等特点[13].

简化前三角形网格TM中每一个三角形Ti三个顶点相关所有三角形组成一个集合为三角形Ti相关三角形集合C.在三维欧氏空间中，将网格中相关三角形所在平面方程定义为ax+by+cz+d=0，且满足a2+b2+c2=1(d为任意常数)，保证多个三角面在同一平面上，通过改进算法处理同一平面的三角形.将平面方程定义为P=[abcd]T，新顶点vi0到相关三角形平面距离平方为(PTvi0)2，将新顶点vi0到相关三角形所在平面距离的最大值作为误差度量标准，误差度量按标准越小，模型简化效果越好.文献[5]规定折叠误差为

(3)

其中：P∈C，C为三角形Ti相关三角形集合；QP是4×4的误差矩阵，是使得折叠误差α(Ti)最小的误差矩阵，

2.2 二次误差测度算法改进

2.2.1 邻接三角形平均面积

模型折叠后与原始模型相似度取决于折叠三角形面积大小[14]，因此在折叠过程中应对折叠三角形邻接区域面积进行评估，判断对折叠三角形影响程度.平均面积指折叠前后，折叠区域附近模型表面变化面积.

牵引变电所设备模型中，特征明显区域三角形网格分布密集，三角形网格面积分布小，邻接三角形面积也相对较小；而在平面区域，例如牵引变压器表面，三角形网格分布稀疏，邻接区域面积较大.折叠过程迭代多次后，模型表面面积变化较大，模型特征信息丢失明显，会使轻量化处理后效果变差.为尽可能使简化后模型保持细节特征，将邻接三角形平均面积作为约束因子添加到折叠误差计算过程中，对模型不同特征区域进行局部简化，改善折叠效果.

三角形邻接区域由三角形T0与其相邻三角形T1～Tj组成，如图2所示.

邻接三角形平均面积表示为

(4)

其中：STi为三角形T0第i个邻接三角形面积；C(T0)为与三角形T0相关三角面集合；count(T0)为与三角形T0相关三角面数量.

2.2.2 多邻域曲率

为减小邻接三角形对折叠三角形的影响程度，将多邻域曲率加入到折叠代价计算中.对于牵引变电所设备，在设备绝缘子边缘特征明显区域，三角面分布较为密集，局部区域面积小，曲率大；在轻量化处理过程中应重点保留特征明显区域，防止几何元素丢失过多，造成模型局部特征失真[15].文献[6]指出，多邻域曲率量化表示模型在某一局部邻接区域特征.若三角面曲率大，则表示模型在该区域存在曲面特征区域，应着重保留该区域三角面.根据曲率大小与模型细节特征相关这一现象，用多邻域曲率判断三维模型细节特征区域.多邻域曲率定义为

(5)

其中，nTi为三角形T0第i个邻接三角形法向量.

由式(5)可见，多邻域曲率决定折叠过程中三角形折叠顺序.KT0较小时，说明此区域不属于特征区域，三维模型细节特征不明显，优先进行多次折叠；KT0较大时，说明该区域内存在细节特征区域，应暂缓执行折叠；在KT0越大区域，尽量减少三角形折叠，避免折叠后三维模型失真、变形.将多邻域曲率加入到折叠误差计算中，可有效保留设备细节特征.

2.2.3 顶点重要度

三维模型特征区域集中在较小区域，例如绝缘子边缘位置；现有算法是将三角形狭长度作为判断依据，算法复杂度高.顶点重要度指折叠过程中三角形顶点重要程度，它表示在其他指标不变情况下，顶点变化对简化后结果的影响.顶点重要度大小与顶点重要程度有关，采用顶点重要度判定三角形区域特征变化[16].

将待折叠三角形权重系数全部初始化，通过计算曲率得出相对较为平坦区域，在平坦区域中，将三角形顶点权重累加，求平均值后可得出该三角形顶点重要度.三角形顶点重要度定义如下：

(6)

其中，WT1i、WT2i、WT3i为三角形三个顶点重要度.顶点重要度计算方法是对三角形三个顶点重要度取平均值.

2.2.4 改进折叠误差

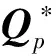
(7)

其中，ST0、KT0、WT0分别通过式(4)～(6)求得.

改进后折叠误差α*(Ti)表示为

Qp)vi0].

(8)

2.2.5 新顶点选取

三角形网格中三角形分为两种：一种为内部三角形，即三角形三条边都存在邻接三角形；另一种为边界三角形，即存在至少一条边在模型边界的三角形[17].

为尽可能保留牵引变电所设备三维模型局部特征，规定：当三角形属于内部三角形，需要通过计算折叠误差，求出折叠误差最小点，作为新顶点；当三角形属于边界三角形，且只有一条边为边界边时，需要对边界边两个顶点进行加权平均，求得新顶点；当三角形属于边界三角形，且两条边为边界边时，只有一个顶点为边界顶点，则该顶点为新顶点.

三角形折叠过程中，对折叠三角形进行分类，可简化新顶点计算步骤，对于不同特征区域进行分类折叠，避免重复计算，有效保留牵引变电所设备模型细节特征，提高折叠效率[18].

2.3 算法流程

在算法执行过程中，首先对模型中三角形进行分类，对于不同种类三角形运用不同新顶点确定办法；其次利用改进二次误差测度方法计算折叠误差矩阵和折叠代价.针对牵引变电所设备模型，折叠代价中加入邻接三角形平均面积、多邻域曲率、顶点重要度3个影响因子，最后将三角形折叠进行迭代，进行牵引变电所设备模型简化.

算法流程如下：

1) 按照所处位置对三角形网格中三角形进行分类并保存.

3) 从待折叠三角形中选取折叠误差最小的三角形优先进行折叠，判断三角形类别；若为边界三角形，再次判断该边界三角形类型，针对不同类型进行新顶点选取.若为内部三角形，则进行折叠误差计算，选折叠误差最小点为新顶点.

4) 若已经达到预期简化效果，则结束算法；若没有达到预期效果，则返回步骤3)继续进行简化.

3 模型轻量化效果

3.1 算法改进效果

牵引变电所中，高压侧隔离开关轻量化处理算法简化误差对比如图3所示，可见QEM算法在简化率较低情况下，简化误差与改进后算法相差不大，但是当简化率达到50%以后，QEM算法简化误差大，设备细节简化出现失真，简化后模型与原始模型视觉差异大；改进QEM算法较QEM算法简化误差小，随着简化率增大，改进QEM算法简化误差更小.当简化率达到95%时，简化误差较QEM算法降低30%.

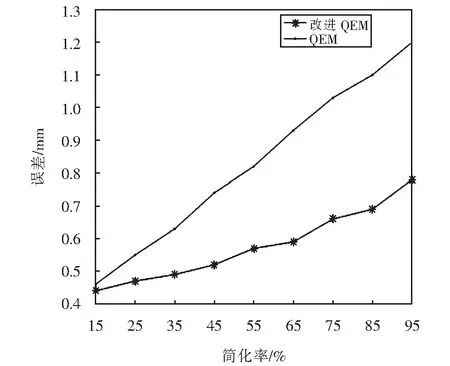
图3 算法简化误差对比Fig.3 Algorithm to simplify error comparison

算法运行时间曲线如图4所示.改进QEM算法运行时间明显低于QEM算法.由于改进QEM算法中加入邻接三角形平均面积、多邻域曲率、顶点重要度，在简化阶段可缩短特征区域简化时间，减少非特征区域简化时间.在保证简化质量前提下，优化算法运行时间，可以提高轻量化处理效率.

对高压隔离开关绝缘子进行简化处理，简化率为75%，分别采用改进QEM算法与QEM算法对其进行简化处理，简化效果如图5～6所示.

模型简化前后三角面数量和点数量变化如表1所列.

由图5～6可得，改进QEM算法在设备绝缘子边缘位置特征保持效果优于QEM算法.由表1数据可知，简化率为75%时，改进QEM算法三角面数量、点数量均低于QEM算法.

对表1进行分析得出，不同简化情况下，改进QEM算法简化后三角面数量、点数量均低于QEM算法.模型三角面数量、点数量越少，模型加载速度越快[18].由此可以得出，改进QEM算法效果较好.

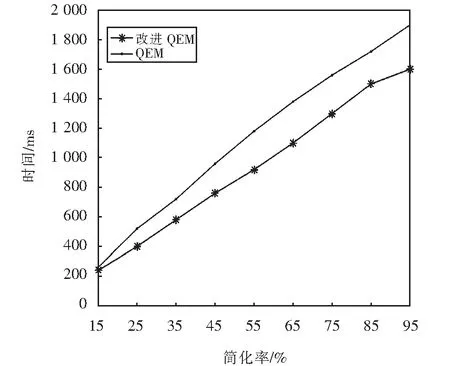
图4 算法运行时间对比Fig.4 Algorithm running time comparison

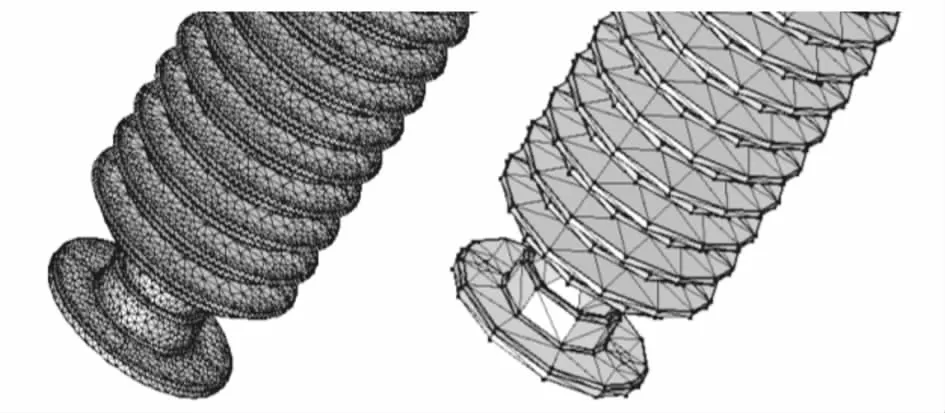
图5 改进QEM算法轻量化处理后三角网格对比图Fig.5 Comparison of triangular meshes after improved QEM algorithm lightweight processing

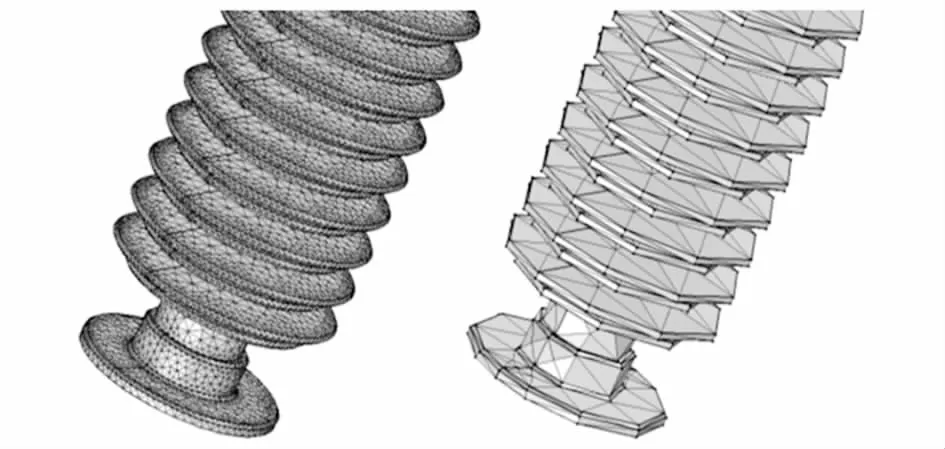
图6 QEM算法轻量化处理后三角网格对比图Fig.6 Comparison of triangular meshes after QEM algorithm lightweight processing

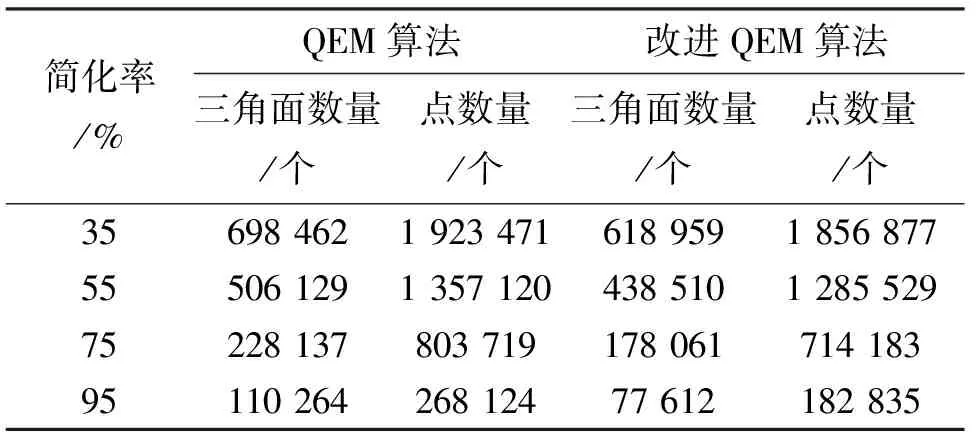
表1 简化数据

使用改进QEM算法简化率为35%时，模型细节特征清晰，边界无失真现象，如图7所示，模型保持设备真实性；当简化率达到75%时，模型表面出现细微失真现象，如图8所示，但不影响牵引变电所模型真实度.由此可得出，改进算法简化后模型更接近真实模型，简化效果较好.

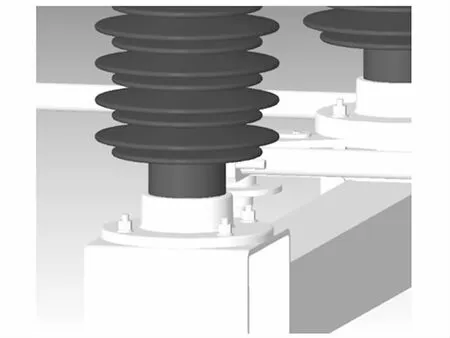
图7 简化35%BIM模型Fig.7 Simplified 35% BIM model

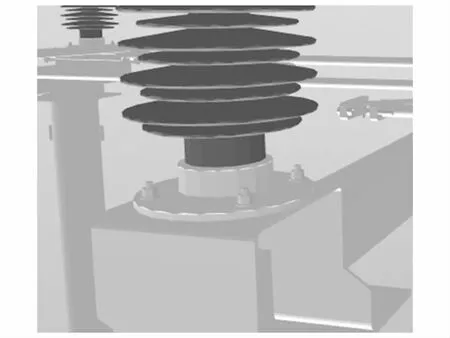
图8 简化75%BIM模型Fig.8 Simplified 75% BIM model

3.2 模型轻量化显示效果

以牵引变电所室外设备高压侧隔离开关为例，使用改进QEM算法进行轻量化处理，图9为牵引变电所高压侧隔离开关BIM模型，图10为轻量化处理后隔离开关BIM模型.

从图9～10中可得，使用改进QEM算法对设备三维模型进行轻量化处理，设备外观细节特征没有发生明显变化，隔离开关绝缘子边缘特征较为完整.简化后模型较为完整的保持模型边界特征.

从图11～12可得出，轻量化处理后，设备模型细节特征保持完整，在设备边缘曲线区域无失真，曲线过度平滑.可见，在模型轻量化处理过程中加入模型表面特征约束因子，既可保持模型细节特征，又减少了模型数据量，能够较好实现模型轻量化.

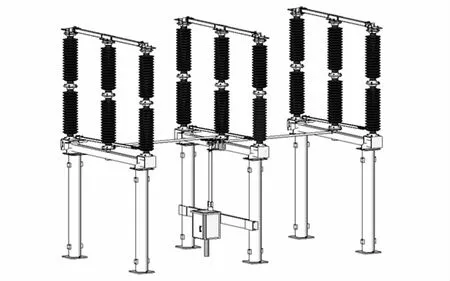
图9 隔离开关BIM模型Fig.9 Isolation switch BIM model

图10 轻量化处理后隔离开关BIM模型Fig.10 BIM model of isolating switch after lightweight processing

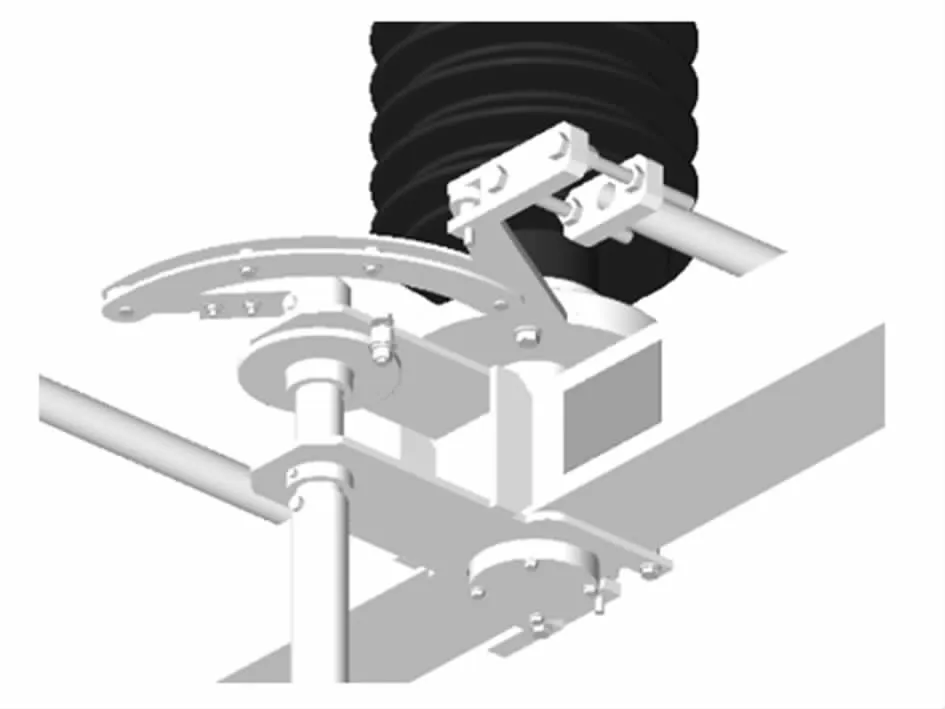
图11 隔离开关动作机构BIM模型Fig.11 BIM model of isolation switch action mechanism

图12 轻量化处理后隔离开关动作机构BIM模型Fig.12 BIM model of isolation switch action mechanism after lightweight processing

4 结论

1) 针对牵引变电所设备模型特征，对二次误差测度算法进行改进，在折叠过程中加入邻接三角形平均面积、多邻域曲率、顶点重要度，改善折叠误差计算，能重点保留模型特征区域表面特征.

2) 通过实验分析，得出改进QEM算法在模型简化误差与运行效率方面均优于QEM算法.在相同简化率情况下，改进QEM算法简化后误差较QEM算法降低约30%.同时，改进QEM算法性能整体优于QEM算法，算法运行效率高.

3) 使用改进QEM算法进行牵引变电所模型轻量化处理，在保持模型表面细节特征条件下降低模型数据量，能够对铁路信息化发展中BIM技术应用起到重要指导作用.

改进QEM算法仅针对模型表面几何数据进行轻量化处理，未考虑模型颜色、纹理等物理属性信息.今后可将模型几何数据与物理属性同时进行分类处理，实现模型整体轻量化处理.