一体化包覆药柱缠绕应力的数值计算
2021-09-08潘浩东舒慧明尹艳华
潘浩东,王 瑞,舒慧明,尹艳华
(1.北京理工大学,北京 100081;2.西安近代化学研究所,西安 710065)
0 引言
固体火箭发动机作为动力装置在航空航天等领域都有广泛的应用[1],对于推进剂的结构完整性分析以及壳体材料的强度考量在实际工艺中都是尤为重要的[2]。发动机对于壳体的要求比较高,普通的材料很难具有比较高的抗压强度,在进入21世纪后,各种新材料的发展很迅速,很多复合材料进入实用阶段,研究也表明,复合材料作为壳体材料相比普通材料是更加优良的选择[3]。复合材料壳体制作工艺也有很多,应用比较广泛的一种是纤维缠绕技术,树脂基碳纤维固化后形成的复合材料强度非常高,且成型效率高,成本低[4]。一般纤维缠绕壳体固化有“外固化”[5]和“内固化”[6]两种,但这两种方法都是将壳体单独固化[7],成型后的壳体或与推进剂药柱无法形成良好的尺寸匹配,造成空隙间隔,影响装药效果且造成资源浪费。而国外曾致力于研究一体化包覆技术,将药柱进行处理,直接在其表面包覆并进行缠绕成壳,然后整件进行固化。经过多年发展,已基本形成了一体化包覆自动化设备及工艺[8],其具体工艺流程见图1。

图1 一体化包覆工艺流程
对于纤维缠绕的数值分析,国内外也有过很多研究。MOROZOV进行了纤维缠绕复合材料壳的建模和应力分析[9];UDDIN等[10]介绍了有限元建模和应力分析的结果以及纤维复合盘与不同类型的缠绕镶嵌方式;胡宽等[11]基于网格理论改变缠绕各参数,提出了壳体材料选择时选择高比强度材料的观点[11];陈汝训[12]也基于网格理论,得到了固体火箭发动机纤维缠绕壳体的圆筒壁厚和爆破压强的计算方法,给出了用模拟实验压力容器确定纤维发挥强度的方法。大多数学者的研究只基于壳体本身,而一体化缠绕则必须要考虑药柱的应力状态,由于药柱的性能与复合材料有很大差异,在缠绕过程中必须严格保证推进剂药柱的结构完整性,控制药柱的应力以避免其发生失效破损。因此,本文基于一体化包覆工艺,以缠绕工段为试验基础,主要研究工况中药柱的应力状态,并能总结一定规律,可为实际工艺提供参考。
1 弹性力学理论
在纤维缠绕包覆过程中,由于药柱、底涂层以及纤维各自的力学性能都有差异,本文的药柱视为各向同性材料,而纤维材料为各向异性,它的强度在各个方向上都是有差异的。要想探究缠绕过程中药柱的应力状态,就要在弹性力学理论基础上进行有限元计算,弹性体在涉及应力与变形时有三套方程[13-15]。
1.1 平衡方程
在空间中坐标系中,材料任何一点应力可以用三个法应力分量σx、σy、σz和三个剪应力分量τxy、τyz、τzx表示。Fx、Fy、Fz分别表示分别代表x、y、z三个方向上的外力,则各应力分量之间存在以下关系。
(1)
1.2 几何方程
与应力状态类似,材料任何一点的应变也可以用三个法应变分量εx、εy、εz和三个剪应变分量γxy、γyz、γzx来表示。u、v、w分别代表物体在x、y、z三个方向上位移分量。则各应变分量之间存在以下关系:
(2)
1.3 本构方程
各向异性弹性体应力-应变本构关系如式(3)。
(3)
对于不同的材料,其本构方程还可简化变形,本文所用的T700纤维视为横观各项同性材料,应力-应变关系如式(4),而推进剂药柱视为各向同性材料,其应力-应变关系如式(5)。
(4)
(5)
2 模型及计算条件
2.1 材料参数
本文采用某一改性双基推进剂,包覆前药柱已经固化,结构由内至外依次为药柱、底涂层、隔热层、缠绕层,其中缠绕层为170/T700树脂基复合材料。建模时将底涂层与隔热层合并为一层(材料选用三元乙丙橡胶),具体结构尺寸见图2。由于缠绕时复合材料并未固化,故取碳纤维力学参数,各层材料力学性能见表1。表1中,ρ为质量密度,E为杨氏模量,μ为泊松比,G为剪切模量。

图2 药柱结构

表1 材料力学参数
2.2 有限元模型
利用Abaqus内部绘图工具进行建模导入部件,推进剂柱体和纤维束均用实体单元模拟,为了简化计算时长,这里只取一小段推进剂药柱,建立并赋予材料属性,构建了一个内部芯模部件,赋予刚体性质,有限元模型及网格划分如图3和图4所示。

图3 有限元模型

图4 网格
推进剂柱体和纤维束网格单元选取C3D8R实体单元(八结点线性六面体单元, 减缩积分, 沙漏控制),柱体采用扫略网格生成技术,扫略方向沿柱体轴向;纤维采用自由划分网格技术;芯模网格单元为C3D8八结点线性六面体(芯模虽有网格,但因被赋予刚体性质并无计算结果)。
2.3 加载与计算
对求解模型施加载荷和约束,其中芯模和药柱、药柱和隔热层之间施加了绑定约束,以芯模中心点为运动参考点;对隔热层纤维施加面面接触相互作用,隔热层为主面,纤维为从面;在纤维两端设置参考点并施加耦合约束,在参考点上施加集中载荷。对芯模赋予绕中心轴(即z轴)的转速和沿z轴负方向的位移速度,在纤维末端赋予沿着纤维方向(即x轴正方向)的预紧力。具体示意图如图5所示。

图5 载荷和约束
为探究哪些载荷因素会对缠绕应力有较大的影响,对纤维预紧力、药柱转速和位移速度以及纤维的带宽共4个因素分别设置5个点,具体值如表2所示。

表2 载荷参数
这里不考虑各载荷之间的相互作用,只研究某一单独变量在改变时,对缠绕过程其应力数值大小的影响。因此,在改变其中一个变量时,其他3个变量都取中间量,即表中第3列对应的值。每一项变量计算5组,探究应力随之改变规律,分析各参数对于缠绕应力的影响大小。
3 求解及结果分析
3.1 缠绕过程应力分析
依据表2取工况A5进行分析,其工况各载荷参数分别为预紧力60 N,位移速度6 mm/s,转速6.28 rad/s,纤维带宽6 mm,模型各部件应力如图6所示。
由图6(a)、(b)可知,在纤维缠绕过程中,相比较隔热层和药柱表面的应力值,纤维带的应力值数量级较大,其末端受力处最大应力能达到272.7 MPa,主体部分的应力93.2~183.0 MPa范围内。缠绕中拉伸力直接作用在纤维上,且纤维束很薄,厚度约为0.1 mm,预紧拉伸力作用的纤维末端横截面积小,导致纤维承受压强大,故纤维内部应力也会很大,这也要求缠绕工况下的纤维要具有较高的抗拉强度。
图6(c)、(d)中隔热层和药柱表面应力分布都很均匀,隔热层表面应力略大于药柱。药柱在纤维起始点有应力值集中于0.18~0.20 MPa内,缠绕区域应力范围在0.06~0.12 MPa内,中心至两边呈递减状态,而纤维未覆盖区域应力值在0.014~0.052 MPa内,整体应力存在明显的梯度。由于设置了位移速度,应力云图能看出明显的位移轨迹,对比下可观察到最终时刻的相对位移小于预先设置的6 mm/s,这是因为纤维与柱体设置了摩擦系数,二者之间并不是完全光滑的运动,导致柱体位移时会带着纤维带一起运动。

(a)Assembly parts (b)Carbon fiber

(c)Theremal-protectivecoating (d)Grain
将药柱单独分析,列出各方向分应力见图7。可知,X、Y方向的分应力大小接近,最大值都在0.012 MPa左右。柱体为圆柱体结构,同时推进剂又具有各向同性的力学性质,导致其在径向方向的分应力大小差别并不大。而药柱Z方向上的分应力云图样貌虽与X、Y方向类似,但应力大小却不同,最大值能达到0.023 MPa,缠绕过程中药柱轴向应力大于径向应力。这是由于纤维带与药柱轴向具有相对位移,加之药柱和芯模在转动过程中轴向也是具有摩擦,而圆柱体结构也决定了轴向和径向不对称的性质。
纤维缠绕是一个动态过程,在缠绕一圈的整个过程中,也需要对应力变化进行分析。图8为药柱剖面图,从外至内依次选了5个节点进行分析,其中节点1为药柱表面,节点2为药柱近表面区域,节点3为药柱中间区域,节点4为花芯凹槽区域,节点5为花芯凸起区域,将这5个节点的应力数据输出并绘制曲线,见图9。

图7 推进剂柱体各分向应力
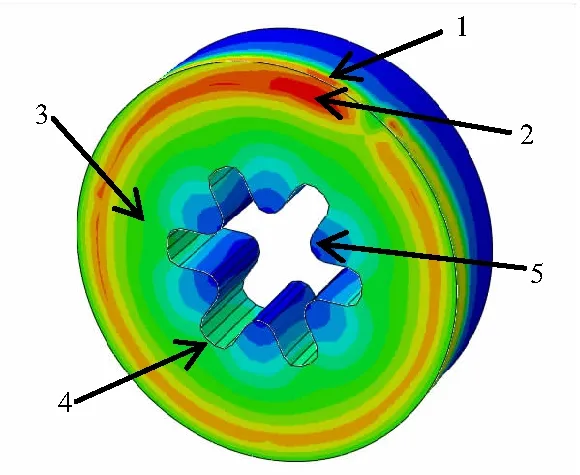
图8 药柱节点
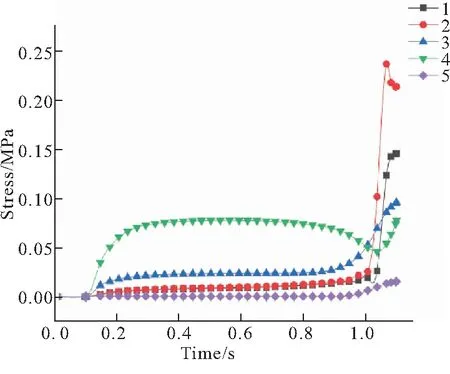
图9 节点应力曲线
从图9可见,各节点在缠绕过程中应力变化还有一定区别。全过程为1.1 s,前0.1 s为预紧阶段,各节点曲线重合,应力近乎于零;后1 s为缠绕阶段,各节点应力开始增长。在刚开始缠绕时,花芯凹槽区域应力短时间增大,而其他节点应力上升还很平缓。因此,这不是拉伸力的影响,而是在转动过程中,芯模和凹槽摩擦挤压产生的应力,之后在转动过程中,各节点应力变化都很平稳,没有很大波动。而在最后0.1 s时,各节点变化产生不同,药柱表面节点和近表面节点都迅速增大,而应力最大并不在药柱表面,而在近表面区域,药柱表面应力达到0.15 MPa,而近表面最大能达到0.23 MPa,比最后缠绕结束时还稍大一点;药柱中心区域和花芯凹槽区域应力上升接近0.1 MPa,只有花芯凸起区域始终变化较小,一直在0.02 MPa以下。
3.2 各因素对缠绕应力的影响
明确缠绕过程中药柱的应力状态后,进而分析各因素对于缠绕应力的影响大小,借此在实际工艺中能通过控制一些参数的大小来避免药柱因应力太大而发生破损。依据表2中数据设置各计算模型载荷参数,计算汇总应力结果,见表3。

表3 各工况药柱应力
由表3可知,预紧力和纤维带宽的改变对于柱体应力影响较大,预紧力增加,药柱表面的应力也会增加,而纤维带越宽,则会导致药柱应力减小。虽然预紧力并不直接作用于柱体,但柱体的旋转是匀速的运动,不会影响纤维带上力的传导,预紧力沿着纤维带传导至柱体上的分力也相应增加,柱体产生的应力也随之增大。40 N预紧力下,药柱应力最大值为0.134 9 MPa,60 N预紧力下,药柱应力最大值能达到0.202 MPa,其数值增加幅度还是较高的。
5 mm带宽纤维的药柱应力最大值为0.220 2 MPa,而7 mm纤维带宽的药柱应力最大值只有0.146 2 MPa。纤维带宽度的增加使得缠绕在药柱表面的纤维面积变大,在同样的预紧力作用下,其受力强度会变小,药柱表面所产生的应力减小。带宽的不同所导致应力差的幅度与预紧力一样都很大,通过改变带宽来控制应力也是可选的方法。可见,纤维带越宽,药柱的应力越小。计算中还发现,预紧力和纤维带宽对纤维带所受应力也有相同影响效果,在实际工艺中,改变纤维带宽和预紧力同时来控制纤维带的应力大小,也是对复合材料的一种有效保护。
从表3中可知,药柱位移速度和旋转速度对缠绕应力的影响并不大,随着位移速度的增加,药柱表面应力会有一定的减小。之前已经分析过,因为柱体位移速度和摩擦力的存在,纤维带缠绕一圈时会有位移轨迹但是跨度不大,导致纤维带在一圈交接处会有部分的应力重叠区域,这些重叠区域的应力会稍大一些,而随着位移速度的增加,在缠绕一圈后其重叠区域会变小,导致了药柱表面应力会有一定量的减小。但应力减小的数值并不是很大,表3中,4.0 mm/s下药柱应力最大值为0.168 9 MPa,8.0 mm/s下药柱应力最大值为0.167 9 MPa,数值差异不大,位移速度的增加并没有明显减小药柱的应力负荷。因此,改变药柱位移速度,并不能有效控制药柱的应力数值大小。
关于转速这一组的计算,不同与其他三组计算设置为缠绕一圈。在不同转速的情况下,如果都转一圈那么耗费的时间是不同的,而不同时间下柱体的位移又会不同,则又涉及到位移速度,所以其数据并不具备代表性,违背了只考虑单一因素影响的初衷。因此,这一组全部设置缠绕0.5 s,缠绕时间取0.5 s就保证了即使是转速为9.42 rad/s的缠绕工况,它的整个缠绕过程也在一圈以内,这里暂时不考虑纤维带多层缠绕带来的叠加应力。由表3数据可知,等时间内随着转速的提高,虽然缠绕区域增加,但是药柱的应力值并没有提升很大幅度,3.14 rad/s转速下药柱应力最大值为0.167 3 MPa,而9.42 rad/s转速下药柱应力最大值也才0.168 3 MPa,这个改变幅度甚至比位移速度所带来的影响还要小。可见,药柱的转速快慢对于缠绕应力影响也不大。
3.3 多层缠绕应力
只计算一圈缠绕与实际的工况还是有很大出入,而要想对实际工艺有所指导,对多圈缠绕进行模拟计算就很有必要。本文所基于的实际工况是缠绕16层,然而作为一个动态非线性计算过程,缠绕16圈对于计算机时负荷太大。通过前文所得结果分析已经知道药柱的移速和转速对应力影响不大,而整个缠绕一圈过程中应力状态其实就是由于预紧力的传导,由图8也可知,在缠绕阶段应力较为规律。基于此基础之上,将药柱模型长度缩小至6 mm(和纤维带等宽),在药柱外层添加复合层,不施加移速和转速而只施加纤维预紧力60 N进行静态分析,具体装配见图10,其他约束及相互作用设置与上文动态模拟均一致。

图10 多层缠绕模型
每一圈缠绕复合层设置相应的层数和宽度,图11为1层和16层的药柱应力云图,可看出静态模拟和动态模拟应力云图还是有一些出入,但是应力范围大体一致,静态缠绕一圈时,药柱整体应力范围在0.07~0.13 MPa之间,而上文图6所示缠绕区域应力在0.06~0.12 MPa之间,图8中节点应力分析表明,主要区域节点3的应力值最后达到0.1 MPa左右。静态分析一圈药柱应力极大值为0.203 MPa,与动态分析的0.202 MPa相差无几,以上都能证明静态分析具有准确性。同时,由于静态分析去除了这药柱移速和转速两个动态载荷量,它与动态分析数据的吻合,也从侧面印证了药柱移速和转速对缠绕应力影响程度很低。
图12为1~16圈缠绕药柱最大应力绘制曲线图,可看出药柱应力随着铺层数的增加在上升,但上升速度越来越慢,最后趋近于平缓,第一圈0.2 MPa,第二圈0.24 MPa,到了第9圈达到0.325 MPa,后面层数应力增加量都很低。由图10可知,第16圈最大应力为0.338 2 MPa。可见,在多层缠绕时,前几圈的缠绕已经决定了药柱大致的应力范围,后面层数的增加对药柱影响会越来越小,这是因为在缠绕过程中碳纤维层彼此之间的应力也相互抵消。此前,对60 N预紧力工况下进行一体化包覆实验,通过光纤光栅传感器侧得缠绕段最大应力为0.353 MPa,与仿真计算所得0.338 2 MPa误差在10%以内。因此,仿真计算结果具有较高准确性,可提供一定理论指导效果。

(a)1 layer
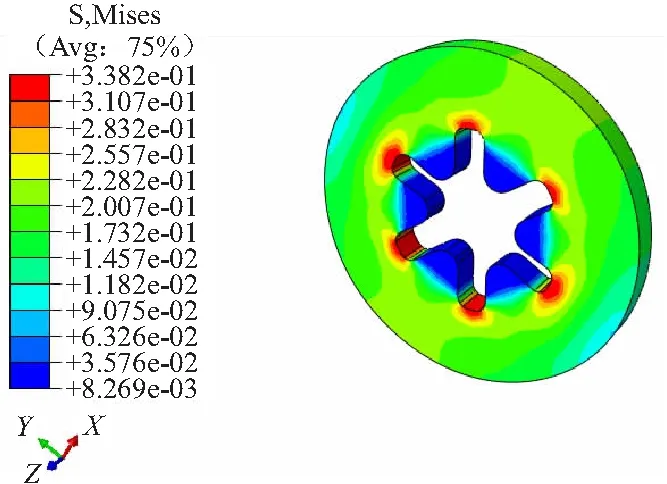
(b)16 layers

图12 多层缠绕药柱应力曲线
4 结论
(1)缠绕过程中纤维带上应力远大于隔热层和药柱,这是由于材料力学性能差异导致的,药柱各分向应力也满足其各向同性的材料属性,在缠绕过程中,各节点应力都呈现一定规律。
(2)预紧力的大小和纤维带宽对于缠绕应力有明显影响,预紧力越大,应力越大,纤维带宽度越大,缠绕应力越小,而药柱位移速度和旋转速度对于药柱缠绕应力影响很小。实际工艺中,应在可选范围通过改变预紧力大小及纤维带宽来控制缠绕应力,对药柱和纤维带都有保护作用。
(3)在多圈缠绕过程中,前几层决定了药柱的大致的应力范围,在缠绕9圈后应力增加缓慢。仿真结果与实验数据相符,可通过仿真计算来预测工况中药柱的应力状态,改变工况参数,避免药柱破损失效。
