(T700/环氧)/EPDM粘接界面参数的实验测试及反演分析

赵朝坤，刘应雷，刘 凯，魏 超

(1.中国航天科技集团有限公司第四研究院，西安 710025；2.中国航天科技集团有限公司四院四十一所，西安 710025)

0 引言

近年来，随着轻质高承载纤维材料的广泛应用以及异型连续缠绕工艺的不断成熟，“飞马座”采用的“缠绕固定+弹性缓冲”复合吊耳结构应用前景广泛。“飞马座”吊耳结构存在纤维壳体/橡胶层粘接界面，粘接界面是最容易发生失效的区域之一，确定粘接界面参数对进行吊耳结构设计具有重要意义。

粘接界面力学特性的表征一直是难点和热点，国内外学者对粘接界面进行了大量实验研究。韦震、周清春等[1-5]采用拉伸实验研究了固体火箭发动机中粘接界面的宏观力学性能。刘龙权等[6]通过单搭接剪切实验测定了金属-复合材料粘接界面参数。ANDERSONS等[7]通过实验研究了复合材料分层扩展方向对断裂韧性的影响。REEDER[8]总结了几种不同复合材料粘接界面Ⅰ型和Ⅱ型断裂韧性与断裂韧性之间的比值关系。BALZANI等[9]采用双悬臂梁模型和复合型断裂弯曲模型测定了单向纤维增强复合材料的层间界面参数。SILVA等[10]研究了粘接结构中界面断裂韧性对结构整体强度的影响。SONG M G等[11]通过实验研究了制备工艺、被粘材料厚度等因素对由复合材料板单搭接接头剪切性能的影响。SORENSEN等[12]采用四点弯曲实验对玻璃纤维增强复合材料的分层情况和整体强度规律进行了研究。CLAY等[13]通过实验测定了金属-复合材料粘接界面的力学性能参数。

完成粘接界面力学实验后，基于实验结果的参数反演识别是表征粘接界面力学特性的关键。VOREL等[14]基于顺序线性分析(sequentially linear analysis)理论，提出了一种识别粘接界面牵引-分离关系的数值方法，该方法表现出优异的数值稳定性和通用性。AIROLDI[15]等采用梯度优化算法，确定了双线性内聚力模型的本构参数。VALOROSO等[16]采用单纯形法和梯度置信区间法，识别了指数内聚力模型的界面参数。ZHAO Haifeng 等[17]采用神经网络提取了金属薄膜/陶瓷界面的界面强度和断裂韧性。WANG J等[18]结合双悬臂梁试验数据、数值仿真结果和遗传算法，确定了率相关内聚力模型的界面参数。XU Y等[19]提出了通过多种实验数据信息识别粘接层界面参数的组合式反演优化算法。刘伟先等[20]采用遗传算法，对复合材料带孔层合板的损伤参数进行了反演识别。林雪慧[21]将梯度优化方法、人工神经网络方法和遗传算法分别引入杂交反演过程中，提取了多相复合材料的非规则界面参数。王娟[22]发展了一种基于实验的一体化反演识别方法。靳国辉[23]基于分步优化法和能量法，提出了一种指数型内聚力模型界面参数的反演方法。陈雄等[24]通过直接搜索算法，对HTPB推进剂与衬层粘接界面的力学性能参数进行了反演分析。韩龙等[25]基于Hooke-Jeeves算法，对HTPB/IPDI复合固体推进剂细观界面参数进行了反演分析。封涛等[26]提出了一种考虑颗粒粒径影响的分布反演优化算法。

本文首先设计了DCSB试件的I型分层扩展实验，结合有限元仿真分析结果，确定了(T700/环氧)/EPDM粘接界面参数的初始值,并以其为基准，基于广义回归神经网络(GRNN)对(T700/环氧)/EPDM粘接界面参数的准确值进行反演分析，为固体发动机关键复合材料界面特性研究与界面质量控制技术提供参考。

1 DCSB试件的Ⅰ型分层扩展实验

参考周清春和贾登等[3-4]的实验方案，为提高裂纹尖端附近应力沿宽度方向的均匀性，对试件宽度B进行优化，设计了图1所示的DCSB试件，表1列出了试件的主要尺寸。

采用T700/环氧复合材料板材，经切割等工序按表1中的尺寸制件，经高温模压制成试件。为预制裂纹、保证剥离位置，在T700/环氧复合材料与EPDM之间放置0.1 mm厚的聚四氟乙烯片预制裂纹，预制裂纹长度a0=30 mm。为提高整个试件的刚度，并保护复合材料表面不受破坏，在复合材料版两侧粘接钢质梁臂；(T700/环氧)/钢界面还具备一定的刚度，在加载过程中，该界面的弹性变形相对较小，以不至于给实验引入系统误差。

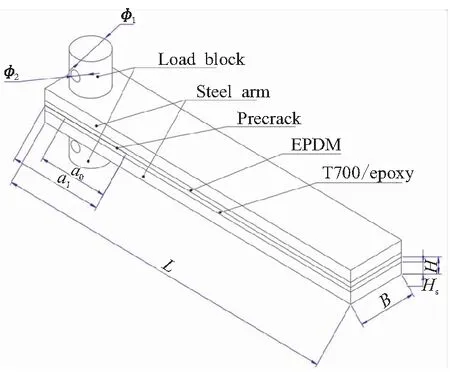
图1 双悬臂夹层梁(DCSB)试件

表1 DCSB试件尺寸

将表观无缺陷、无胶团的3组DCSB试件编号为1、2、3，在INSTRON5982万能材料试验机上分别对其进行Ⅰ型分层扩展实验。试件采用销钉通过夹持孔与试验机上下接头铰接，未加载端不受约束，在室温(21 ℃)以5 mm/min的恒定位移加载速率拉伸DCSB试件，获得的3组载荷-位移曲线如图2所示。

图2 DCSB试件Ⅰ型分层扩展实验的载荷-位移曲线

3号试件因制作过程中的工艺波动导致界面粘接不完全，后期进行了灌胶，实验得到的载荷-位移曲线峰值较低，整体规律与1号、2号不一致。考虑到实际产品通常粘接界面良好，无界面脱粘现象，因此本文只研究完全粘接的界面，在后续处理实验数据过程中舍弃3号实验据。

根据材料力学中的悬臂梁理论，加载点载荷F与加载点位移w具有如下关系：

(1)

式中E为悬臂梁的弹性模量；B为试件宽度；H为试件的半高；a为裂纹长度。

式(1)表明，加载点载荷与位移在加载初期成线性关系，在后续处理实验数据的过程中，对初始阶段进行线性处理，且将起点平移至原点。

2 粘接界面参数反演分析初始值的确定

线弹性断裂力学中，计算粘接界面的断裂韧性的Irwin-Kies公式为[27]

(2)

式中Fmax为临界载荷(峰值载荷)；a0为预制裂纹长度。

式(2)假定被粘接结构为各向同性材料且仅发生小变形，EPDM材料在(T700/环氧)/EPDM粘接试件裂纹扩展过程中存在大变形，同时T700/环氧复合材料为各向异性，采用该公式计算界面参数存在一定误差。本文仅用式(2)的计算结果作为有限元仿真的(T700/环氧)/EPDM粘接界面参数初始值，通过有限元仿真进一步确定参数反演的初始值，不影响最终反演分析结果。根据实验结果，采用式(2)计算(T700/环氧)/EPDM粘接界面的断裂韧性，如表2所示。

表2 DCSB实验的载荷峰值及式(2)确定的断裂韧性

在初步确定GIc后，可在一定范围内假设界面参数σmax，0对DCSB试件进行有限元计算，使计算的载荷-位移曲线与实验曲线匹配，从而获得确定σmax，0的初始值。

采用表1中的尺寸参数，在ABAQUS中建立了DCSB试件的二维有限元模型，裂纹尖端的网格如图3所示。钢质梁臂采用四边形主导的自由网格，最大尺寸为1 mm，最小尺寸为0.1 mm，两侧边设置Single形式的种子分布，单元类型为CPE4和CPE3；T700/环氧复合材料层采用四边形结构化网格，网格尺寸为0.1 mm，单元类型为CPE4；EPDM采用四边形结构化网格且网格尺寸为0.1 mm，单元类型为CPE4H；胶层厚度设置为0.1 mm，采用四边形扫略网格，其单元类型设置为文献[28]中用户自定义的界面单元，单元尺寸为0.1 mm×0.1 mm。

图3 DCSB试件裂纹尖端的有限元模型

钢的弹性模量为210 GPa，泊松比为0.3；为简化计算，T700/环氧复合材料的弹性模量为80 GPa，泊松比为0.25；EPDM的Yeoh超弹本构参数为C10=0.383 MPa、C20=-1.665×10-3MPa、C30=5.753×10-6MPa。载荷及边界条件与DCSB试件的I型分层扩展实验一致。将界面断裂韧性 设置初步确定的值0.137 N/mm，法向初始强度 依次设置为0.1、1、10、100 MPa进行计算，计算结果如图4所示。

图4中，当σmax,0逐渐增大时，载荷-位移曲线的峰值增大，初始段曲线的斜率增大，最大载荷点向左上方移动。σmax,0=10 MPa时，计算的载荷位移曲线与实验曲线的形状较为接近，但峰值点的位移与实验相差较大；σmax,0=1 MPa时，计算的载荷位移曲线与实验曲线初始段的斜率较为接近。当σmax,0=1 MPa时，GIc分别为0.137、0.3、0.5、0.7、0.9 N/mm时，DCSB试件加载点的载荷-位移曲线如图5所示。

图4 GIc=0.137 N/mm时不同σmax,0计算的载荷-位移曲线

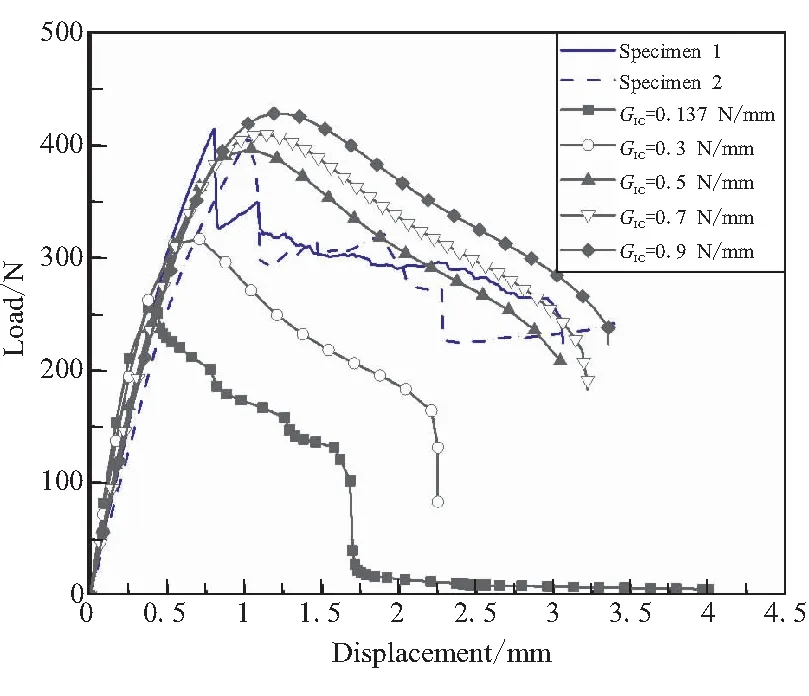
图5 σmax,0=1 MPa时不同GIc计算的载荷-位移曲线

图5中，当GIc逐渐增大时，载荷-位移曲线的峰值增大，初始段曲线的斜率变化较小，最大载荷点向右上方移动；当GIc=0.5 N/mm时，计算的载荷-位移曲线的与实验曲线的形状及峰值点坐标较为接近。经过上述拟合计算，确定了(T700/环氧)/EPDM粘接层界面反演分析参数的初始值为GIc=0.5 N/mm、σmax,0=1.0 MPa。

3 基于GRNN的界面参数反演

以第2章拟合的界面参数为基准，经完全交叉分组的析因设计及对应的有限元分析(FEA)结果构造了FEA输出-界面参数的数据样本，采用广义回归神经网络(GRNN)对(T700/环氧)/EPDM粘接界面参数的准确值进行反演识别。

3.1 参数反演的基本原理

GRNN中，与输入向量X对应的输出向量估计值为

(3)

式中n为训练样本的数量；Xi、Yi分别为第i个训练样本的输入和输出；k为平滑参数。

根据式(3)可构造GRNN神经网络结构。GRNN网络的训练过程中，需不断调整平滑参数k以获得最佳回归估计结果，最优平滑参数与最小误差序列均方值E相对应，具体详见参考文献[29]。

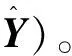
3.2 粘接界面参数反演

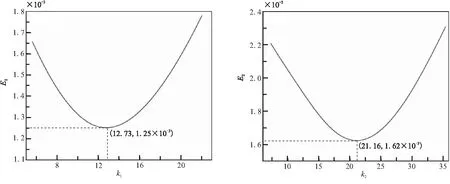
为获得建立GRNN所需的训练样本，将表2中(T700/环氧)/EPDM粘接层界面参数的初始值进行拉偏处理。将σmax,0的值取为0.75、1、1.25、1.5、1.75 MPa，GIc的值依次取为0.4、0.45、0.5、0.55、0.6 N/mm，并进行完全交叉分组计算，可获得25组加载点的载荷-位移曲线。当DCSB试件(T700/环氧)/EPDM粘接层的界面裂纹发生不稳定扩展后，由于试件橡胶层存在大变形，载荷-位移曲线出现较大的波动，规律性较差。因此，仅采用实验载荷-位移曲线的上升段对GIc和σmax,0进行反演识别。训练过程中，kmin1=5.60、kmax1=22、，kmin2=7.28、kmax2=40，1号实验和2号实验的误差序列均方值相对于平滑参数的变化曲线如图6所示，与最小的误差序列均方值对应的最优平滑参数k1=12.73、k2= 21.16。

将25组载荷向量及对应的界面参数作为训练样本，平滑参数分别设置为k1=12.73和k2=21.16对GRNN进行训练，将实验的载荷向量作为输入，反演得到(T700/环氧)/EPDM粘接层的界面参数如表3所示。将表3中的界面参数分别代入DCSB中的有限元模型进行计算，得到加载点的载荷-位移曲线与实验曲线的结果如图7所示。图7中，与采用界面反演参数初始值(GIc=0.5 N/mm、σmax,0=1.0 MPa)仿真结果相比，采用1号和2号实验数据反演的界面参数(见表3)，计算获得的载荷-位移曲线与实验结果吻合更好。1号实验和2号实验的反演结果中，2号实验反演的参数计算的载荷-位移曲线与2号实验结果重合较好，但与1号实验的偏离稍微较大；而1号实验反演的参数计算的载荷-位移曲线介于1号和2号实验曲线之间，峰值载荷为411.27 N，与1号实验和2号实验的载荷峰值411.36 N的差值的平均值只有2.72 N，而通过实验拟合结果计算的峰值点差值的均值达到了41.36 N。因此，通过GRNN的反演，最终确定(T700/环氧)/EPDM粘接层的界面参数为断裂韧性GIc=0.575 N/mm、法向初始强度σmax,0=1.25 MPa。

(a)No.1 test (b)No.2 test

表3 反演的(T700/环氧)/EPDM粘接层界面参数

图7 加载点载荷-位移曲线的对比结果

4 结论

(1)(T700/环氧)/EPDM粘接界面法向初始强度的改变对双悬臂夹层梁I型分层扩展实验加载点载荷-位移曲线峰值和初始段斜率均会产生较大影响；断裂韧性的改变对峰值有较大影响，对初始段的斜率影响较小。

(2)在双悬臂夹层梁Ⅰ型分层扩展实验与有限元仿真分析的基础上，采用广义回归神经网络反演获得(T700/环氧)/EPDM粘接界面的断裂韧性GIc=0.575 N/mm，法向初始强度σmax,0=1.25 MPa；反演结果与实验结果对比分析表明，结合DCSB I型分层扩展实验、有限元仿真分析和广义回归神经网络，可确定(T700/环氧)/EPDM粘接界面参数的准确值。