蜂巢晶格反铁磁材料的自旋动力学
2021-09-06潘江扬龚子瑶吴天兵
潘 婧,潘江扬,龚子瑶,吴天兵,王 含,蓝 郁
(衡阳师范学院物理与电子工程学院,湖南衡阳 421002)
曹原等在魔角石墨烯中发现了超导电性[1,2],使人们对石墨烯等材料及其超导电性的研究再次升温.石墨烯是具有蜂巢形状晶格的真正二维材料,有很多新奇特性[3,4].石墨烯的超导电性和高温超导体铜氧化物的超导电性有着各种相似的以下特性:(1)铜氧化物超导体是准二维材料[5],而石墨烯则是完美的二维材料[6];(2)铜氧化物超导体的母体化合物是莫特绝缘体[7],而石墨烯中实现的半满绝缘态和莫特绝缘体几乎是完全一致的[1];(3)魔角石墨烯超导转变温度随载流子浓度变化的相图呈抛物线形[1],这与铜氧化物超导体的相图也几乎一样.铜氧化物超导的母体化合物具有反铁磁序长程序,对其进行化学掺杂则使反铁磁长程序消失,但仍然保留反铁磁短程关联,随着掺杂浓度的增加出现超导电性,最后超导电性和反铁磁短程关联在高掺杂浓度区一起消失[7,8].铜氧化物超导体的性质十分反常和复杂,至今人们对其超导机理还没有形成一致的认识,但可以肯定的是自旋激发对其超导电性的形成发挥着十分重要的作用[9,10].冯世平等[8,11]认为,正是强的电荷载流子和自旋之间的相互作用通过交换自旋激发,诱导出电荷载流子配对态,进而是电子配对态和超导电性.鉴于石墨烯超导和铜氧化物超导之间的相似性,我们猜测魔角石墨烯中的自旋特性也应该对其超导电性有重要的影响,因此对蜂巢晶格材料的自旋激发进行研究,将会帮助理解石墨烯等蜂巢晶格材料的超导电性和新奇物理特性的本质.
本文将利用格林函数理论来研究蜂巢晶格反铁磁材料的自旋动力学.首先推导蜂巢晶格反铁磁材料在半满时的自旋格林函数,得到一组关联函数的自洽方程组;然后数值求解这个方程组获得这些关联函数的确切值;最后利用这些关联函数的值计算系统的自旋激发谱和动力学自旋结构因子,讨论系统的自旋激发特性.
1 自旋格林函数和动力学自旋结构因子
石墨烯这样的材料是复式晶格[6],其晶体结构包含A和B两个子格子,如图1所示.

图1 石墨烯的晶体结构
石墨烯材料在半满时的反铁磁性可由海森堡模型
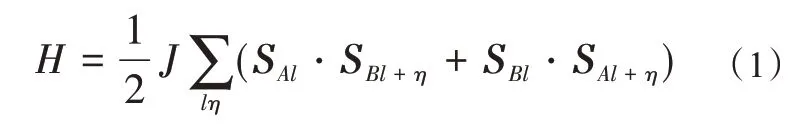
描述[12,13],其中求和遍及所有格点,l+η表示l格点的最近邻格点.引入自旋的升降算符S±=Sx± iSy,则海森堡模型(1)变为

为了求解海森堡模型(2),定义自旋算〉〉符的双时格林函数

DBB(Ri-Rj,t-t')和DBA(Ri-Rj,t-t')的定义与此类似.

可以写成模和辐角的形式γk=|γk|eiθk.
利用自旋格林函数(8)、(9)和(10),容易求得关联函数满足以下自洽方程组

这样退耦参数α、关联函数χ和C就可以自洽求解出来.
由于材料的A、B两个子格子之间存在相互作用,因此可定义成键态和反键态的自旋格林函数
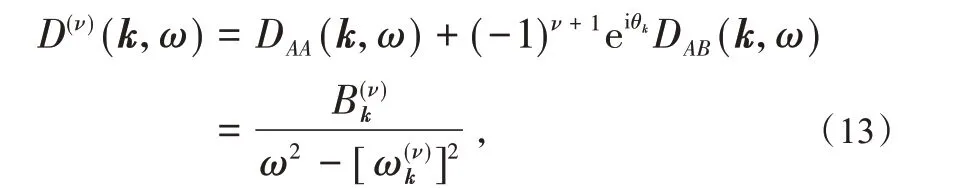
其中,ν=1 和ν=2 分别对应于成键态和反键态,和则分别为成键态和反键态自旋激发谱.成键态和反键态的动力学自旋结构因子则可由成键态和反键态的自旋格林函数求得

其中nB(ω)是玻色分布函数,利用该动力学自旋结构因子即可讨论系统的自旋动力学特性.
2 蜂巢晶格反铁磁材料的关联函数和自旋动力学
我们首先对自洽方程组进行数值计算,并在图2中给出了蜂巢晶格反铁磁材料的最近邻关联函数和次近邻关联函数(i≠i+η+η')随温度变化的曲线.从图2中可以看出,最近邻和次近邻关联函数在零温时达最大值,并且两者均随温度的升高而逐渐降低.零温时,系统处于基态,反铁磁序高度有序,格点间的自旋关联最强,故关联函数达最大值;随着温度的升高,晶格的自旋序受热运动的影响,开始偏离有序状态,所以关联函数随温度的升高而逐渐减弱,并且在高温极限下次近邻关联函数趋于零.另外,在整个温度范围内,次近邻关联函数C1都比最近邻关联函数χ小很多,说明次近邻格点间的自旋关联比最近邻格点间的自旋关联要弱很多.
接着讨论系统的自旋激发特性.图3 给出了蜂巢晶格反铁磁材料的自旋激发谱.从图3中可以看出,由于晶格中A、B两个子格子之间的相互作用,自旋激发谱劈裂为成键态和反键态两支,在同一波矢点比小.在布里渊区中心Γ点,成键态自旋激发谱而反键态自旋激发谱对于布里渊区中心附近的k点,成键态自旋激发谱与波矢的大小成正比,即而反键态自旋激发谱则明显偏离这种正比关系.因此这两支自旋激发谱在布里渊区中心附近的动力学行为明显不同.特别的是,当波矢的值k较小时,自旋激发谱并没有明显体现蜂巢晶格的六角对称性,但随着波矢k的值增大,这种六角对称性就逐渐体现了出来.
我们再来讨论系统的自旋动力学特性.图4 给出了系统在第一布里渊区的成键态和反键态动力学自旋结构因子.从图4中可以看出,成键态和反键态动力学自旋结构因子均出现围绕布里渊区中心的磁散射峰,并且随着能量的增加,磁散射峰向远离布里渊区中心的方向移动.自旋结构因子的这种行为可以从自旋格林函数和自旋激发谱的特性(见图3)中看出,当入射中子的能量等于某波矢点kc自旋激发谱的值时,即就产生共振,使动力学自旋结构因子在相应的波矢点出现散射峰.由于自旋激发谱是随波矢的增大而增大的,所以当入射中子的能量增加时,就需要增大波矢来增大自旋激发谱以适应入射中子的能量而产生共振,因此磁散射峰就向远离布里渊区中心的方向移动.
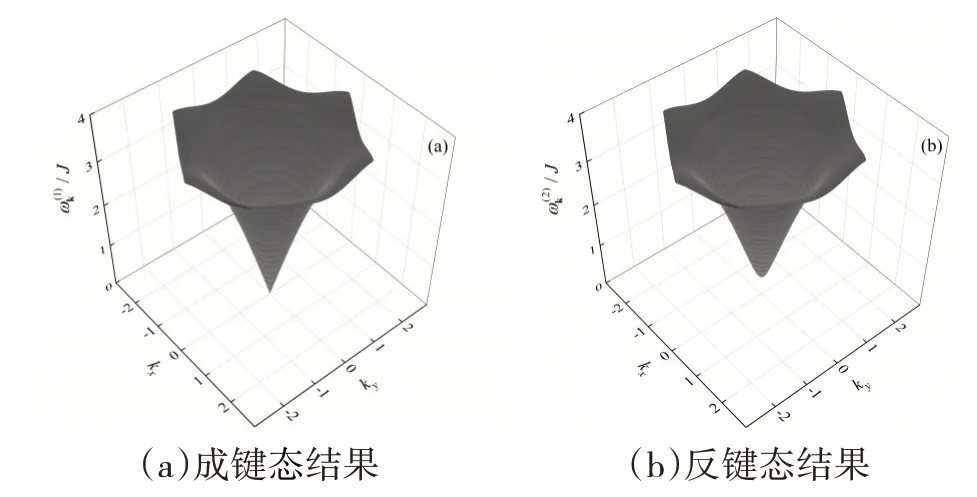
图3 蜂巢晶格反铁磁材料在温度T=0.1 J 时的自旋激发谱

图4 蜂巢晶格反铁磁材料在温度T=0.1 J 时的动力学自旋构因子
3 结论
本文从蜂巢晶格反铁磁材料在半满时的海森堡模型出发,利用Kondo 和Yamaji 提出的二阶退耦近似计算了系统的自旋格林函数,得到一组关于关联函数的自洽方程组.用数值求解该方程组,并据此计算了系统的自旋激发谱和动力学自旋结构因子.计算结果表明,蜂巢晶格反铁磁材料的最近邻和次近邻关联函数均随温度的升高而逐渐降低,这是因为温度的升高使格点的热运动扰乱了系统的反铁磁序,使格点间的自旋关联减弱从而致使关联函数减小.特别的,晶格两个子格子之间的相互作用使系统的自旋激发谱和动力学自旋结构劈裂为成键态和反键态两支.成键态自旋激发谱的值一直比反键态自旋激发谱的小,并且在布里渊区中心附近成键态自旋激发谱与波矢的大小成正比,而反键态自旋激发谱则偏离正比关系.当入射中子的能量等于某波矢点自旋激发谱的值时,动力学自旋结构因子就产生共振从而形成围绕着布里渊区中心的磁散射峰,并且这些磁散射峰随能量的增加逐渐远离布里渊区中心.我们的结果对理解蜂巢晶格材料的超导电性及其新奇物理性质必定有重要的帮助.
