虚力原理在运动学速度分析中的应用
2021-09-06张居敏
张居敏,周 岭
(1.华中农业大学工学院,武汉 430070;2.塔里木大学机械电气化工程学院,新疆阿拉尔 843300)
长期以来人们对虚位移原理进行了深入研究,通过该原理可以用动力学理论求解静力学问题[1-2].既然如此,那虚位移原理是否也可以求解运动学问题?虚位移原理是否存在孪生对偶理论?
本文提出的虚力原理可作为虚位移原理的孪生对偶理论.通过虚力原理可以用静力学理论和动力学理论联合求解运动学中的速度问题,还可用滑动摩擦力理论求解相对速度.虚力原理为求解运动学中速度问题提供了新思路、新方法.
1 虚力原理
定常、理想、双面约束运动学系统在运动过程中的任一时刻,假想系统在该时刻处于静止状态,并假想施加一个力系让静止系统中各物体都受力平衡,这个假想施加的力系称为系统的虚力系,则此虚力系在该时刻系统无限小时间段内发生的实际位移上对应的虚功之和必为零,即

式中:Fi表示第i个虚力,因为是假想施加的力,所以称为虚力;dri表示虚力Fi的作用点在系统无限小时间段dt内发生的实际位移;vi表示虚力Fi作用点的实际速度.
上述就是虚力原理,式(1)称为虚力原理方程.虚力系可以随意选取,只要能让静止状态下系统中各物体都受力平衡就可以了.虚力与真实位移的点乘积或真实力与虚位移的点乘积都是虚功,所以虚力原理方程与虚位移原理方程都是虚功方程.
虚位移原理要求系统处于静止状态,因为该原理证明过程中用到了静止状态初始条件[3].但虚力原理对应的系统一开始可能就处于运动状态.对于一个力系,不论是假想添加到系统上的虚力系,还是实际存在的真实力系,只要能让静止状态下的系统受力平衡,该力系就有能力让静止状态的系统继续保持静止状态,即受力平衡状态,就可以对该静止状态的受力平衡系统应用虚位移原理.对于定常约束系统,虚力原理中的实际无限小位移(简称实位移)属于系统虚位移范畴.因此,虚力原理本质上是在虚位移原理中用虚力替代真实力、用实位移替代虚位移,即虚力原理的本质是虚位移原理必要性成立条件的另一种表述,所以无须再证明.
2 虚力原理求速度的具体应用
对于理论力学课程而言,运动学中速度分析问题重难点在刚体平面运动和点的复合运动章节,下面用虚力原理对不同问题分别予以讨论.
2.1 平面运动问题
例1 如图1a 所示,该机构在力偶M和M1共同作用下处于静止且受力平衡状态,即静力学平衡状态.OA=1 m,AB=1.5 m,BC⊥OC,各杆重量不计.已知OA杆上力偶M的大小,(1)求BC杆上的力偶M1;(2)如图1b 所示,如果在AB杆上作用力偶M2使系统受力平衡,求M2的大小.

图1a

图1b
解(1)AB为二力杆(图1a),其他杆受力如图1c所示.
对OA杆平衡力系(图1c):

对BC杆平衡力系(图1c):

图1c

式中,|BC|=|OA|sin60°+|AB|sin30°=1.62 m.
将式(1)(2)联立可求解得:M1=2.80M.
(2)BC为二力杆(图1b),其他杆受力如图1d/1e所示.
对AB杆平衡力系(图1d):

图1d
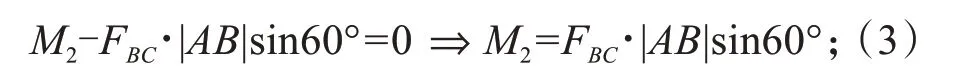
对OA杆平衡力系(图1e):

图1e

将式(3)(4)联立可求解得:M2=2.60M.
例2 在图2a 中,OA杆匀速转动,ω=4 rad/s,带动系统运动,OA=1 m,AB=1.5 m.图示位置时BC⊥OC,求此时BC杆、AB杆各自的角速度.

图2a
解(1)求BC杆角速度ω1.分别在OA、BC杆上添加能让系统受力平衡的虚力偶M和M1,如图1a 所示.把图2a 系统图示时刻无限小时间段内的实际位移作为虚位移添加到图1a所示平衡静止系统上,对图1a系统列虚功方程,即虚力原理方程:

其中,M1=2.80M(见例1(1)问的计算结果).
将M1代入得:

(2)求AB杆角速度ω2.分别在OA、AB杆上添加能让系统受力平衡的虚力偶M和M2,如图1b 所示,列虚力原理方程,即虚功方程:

其中,M2=2.60M(见例1(2)问的计算结果).
将M2代入得:
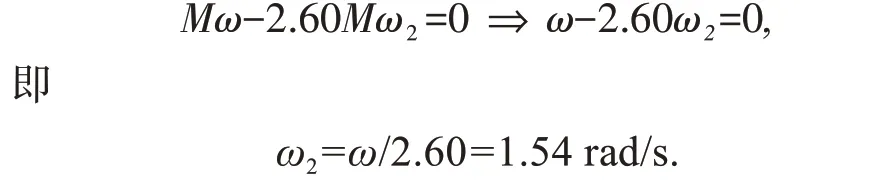
至此,例2题求解完毕.
借助虚力原理,我们在不用运动学理论情况下单纯用静力学理论和动力学理论就可求解出杆BC、AB各自的角速度.
作为比照,下面用运动学理论再次求解例2问题.
如图2b 所示,vA=|OA|ω=4 m/s.AB杆作平面运动,以A为基点,则B点速度:

图2b

该矢量方程分别向水平、竖直方向投影得:

可见用运动学理论与虚力原理理论,两者求解结果相同.这也间接检验了虚力原理的正确性.
2.2 点的复合运动问题
例3 如图3a 所示,偏心轮半径为r,绕轴O转动角速度ω=2 rad/s.图示位置时CO⊥AO,求此时AB杆角速度ω1的值.

图3a
解如图3b所示,设系统在虚力偶M和M1共同作用下静止平衡,忽略弹簧弹力(虚力系可以任意选取,只要能让静止系统受力平衡即可).把图3a 系统在图示位置处无限小时间段内的实际位移作为虚位移添加到图3b 所示系统中,对图3b 系统列虚功方程,即虚力原理方程:

图3b
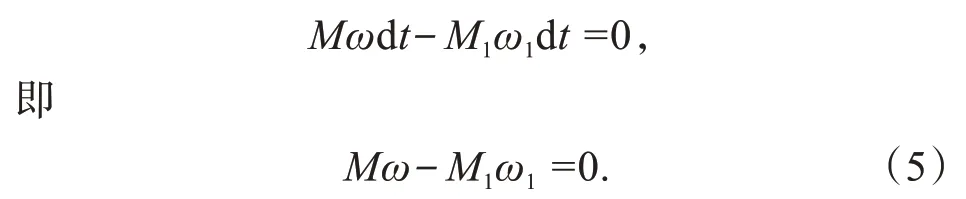
图3b中AB杆对应的平衡力系如图3c所示,

图3c

图3b中圆轮对应的平衡力系如图3d所示,

图3d
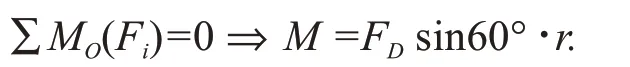
把M和M1表达式同时代入式(5)并整理得:sin60°·rω-rω1/tan30°=0 ⇒ω1=0.5ω=1 rad/s.
至此,例3题求解完毕.
作为比照,下面用运动学理论再次求解例3问题.
如图3e 所示,动点取圆轮轮心点C、动系建立在AB杆上,有

图3e

在式(6)中,va=rω(←);ve=|AC|ω1,ve⊥AC,|AC|=2r;vr平行于AB杆轴线.
式(6)分别向水平、竖直方向投影得:

AB杆角速度:ω1=ve/|AC|=0.5ω=1 rad/s.
可见用运动学理论和虚力原理的求解结果相同.但是用虚力原理求解时只用到了静力学力系平衡理论和动力学理论,不涉及运动学理论;而用运动学理论求解时牵扯到一系两点三运动等相对抽象的点的复合运动理论.
2.3 平面运动与点的复合运动综合问题
例4 如图4a 所示,系统静止平衡.O1A杆水平,长度为r,b=4r,θ=30°,O2B⊥DB.不计各构件自重,求力偶M与力F之间的平衡关系.

图4a
解O1A杆所受平衡力系如图4b所示,且

图4b

DB为二力杆,O2B杆所受平衡力系如图4c 所示,且

图4c 图4d

DC杆所受平衡力系如图4d所示,且
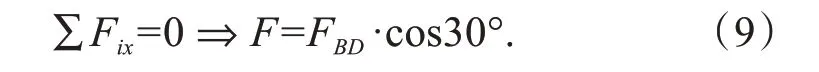
将式(8)(9)同时代入式(7)得:M=F·r.
这就是力偶M与力F之间的力学平衡关系.
例5 如图5a所示,O1A杆长度为r,匀速定轴转动,角速度为ω,带动系统运动.b=4r,图示时刻θ=30°,求此时CD杆速度v的大小.
解分别在O1A杆、CD杆上添加虚力偶M及虚力F使系统受力平衡,如图4a所示.把图5a所示系统在图示时刻无限小时间段内的实际位移作为虚位移添加到图4a 所示平衡静止系统上,对图4a系统列虚功方程,即虚力原理方程:

图5a

即Mω-Fv=0,其中,M=Fr(见例4计算结果).
将M代入上式整理得:v=rω.
至此,例5题求解完毕.
作为比照,下面用运动学理论再次求解例5问题.
如图5b所示,以O1A杆A端点为动点、O2B杆为动系,va=ve+vr,va⊥O1A,ve⊥O2B,vr沿O2B杆轴线;va=vA=rω,ve=va·sin30°=0.5rω,O2B杆角速度

图5b

BD杆作平面运动,由速度投影定理得:

CD杆平行移动,该杆速度:ν=νD=rω.
可见用运动学理论求解结果与上述虚力原理法求解结果相同,这也相互检验了两套理论各自的正确性.
点的复合运动与刚体平面运动一直都是理论力学课程教学的重难点,是很多初学者的薄弱环节.在例5 中,虚力原理解题法比运动学理论求解方法有明显优势:完全避开了点的复合运动理论中动点、动系的选择问题,也避开了速度投影定理等平面运动理论.
在理论力学教材中,物体的运动包含平行移动、定轴转动、平面运动和相对运动(即点的复合运动)等,不同形式的运动对应着不同的速度求解理论及方法.但是在利用虚力原理求解速度时候,不同运动形式刚体却有着相同的求解理论,即在静力学力系平衡理论和动力学理论运用中,我们可以在完全不懂运动学理论的情况下求解出速度问题.
3 滑动摩擦力理论在速度求解中的应用
在利用虚力原理时候,引入摩擦力理论可以简化相对速度问题的分析求解难度.
例6 如图6a 所示,凸轮向右运动,推动AB杆向上运动.图示时刻凸轮速度v=3m/s,α=60°,求此时AB杆速度vA及AB杆B端点在凸轮上的相对滑动速度vr的值.
解如图6b 所示,设系统在虚力F和FA共同作用下静止平衡,并且凸轮与AB杆之间有摩擦力,设滑动摩擦系数为f.把图6a 所示系统在图示时刻无限小时间段内的实际位移以虚位移形式添加到图6b所示系统上,摩擦力做负功,列虚力原理方程:
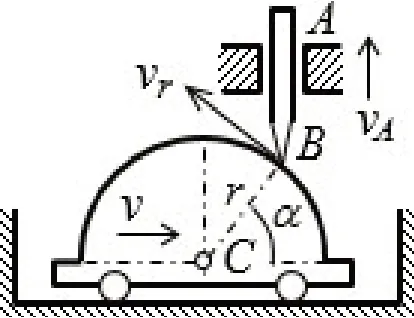
图6a

其中FB表示AB杆B端对凸轮的正压力.
对于图6b所示静止平衡即静力学平衡系统,凸轮、AB杆所受平衡力系依次如图6c、6d所示.

图6b

图6c
对凸轮平衡力系(图6c):
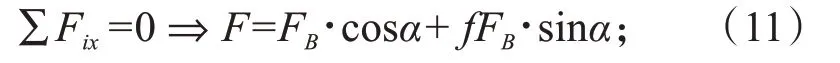
对AB杆平衡力系(图6d):

图6d
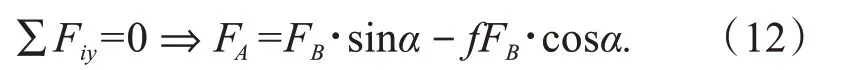
将式(11)(12)同时代入式(10)并整理得:

其中摩擦系数f可以取任何值,例如当f=0.1,f=0.2和f=0.3 时,式(13)都应该成立.这说明式(13)中所有含f项的和等于零,即

将式(14)代入式(13)并整理得:

式(15)是滑动摩擦系数f=0(即不存在摩擦力)时候系统虚力方程的化简结果.实际上不论是否存在摩擦力,凸轮与AB杆之间的速度关系都相同.将式(14)(15)联立求解得:

至此,例6题已求解完毕.
作为比照,下面用运动学理论再次求解例6问题.
如图6e 所示,动点取AB杆B端点,动系建立在凸轮上,ve=v=3 m/s,va=ve+vr,该式分别向水平、竖直方向投影得:

图6e

可见用运动学理论和用虚力原理理论,两者求解结果相同.引入摩擦力理论以后,可以把系统的虚力原理方程式由一个裂变为两个,然后联立求解两个未知数.
例7 如图7a 所示,套环Q同时套在水平杆DE和直角弯杆ABC上.弯杆ABC绕A轴左右摆动,AB=0.2 m,A点到水平杆DE的垂直距离也为0.2 m.图示时刻ω=5 rad/s,求此时套环Q的绝对速度v和沿ABC杆滑动的相对速度vr的值.
解如图7b 所示,在套环Q上添加虚力F,在弯杆ABC上添加虚力偶M,设系统在F和M共同作用下静止平衡,并且套环Q与弯杆ABC杆之间存在摩擦力,设滑动摩擦系数为f.把图7a 所示系统在图示时刻无限小时间段内的实际位移以虚位移形式添加到图7b 所示静止平衡系统上,滑动摩擦力做负功,列虚力原理方程得:

图7a

式中FN表示弯杆ABC对套环Q的正压力.
图7b所示系统静止且受力平衡,套环Q、弯杆ABC所受平衡力系依次如图7c、7d所示.

图7b
对套环Q平衡力系(图7c):
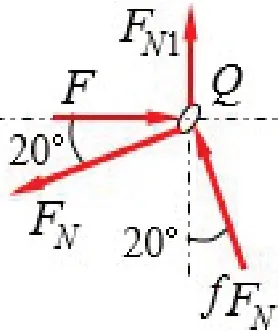
图7c

对弯杆ABC平衡力系(图7d):

图7d

由图7e可知,|BQ|=|AB|tan35°=0.140 m.
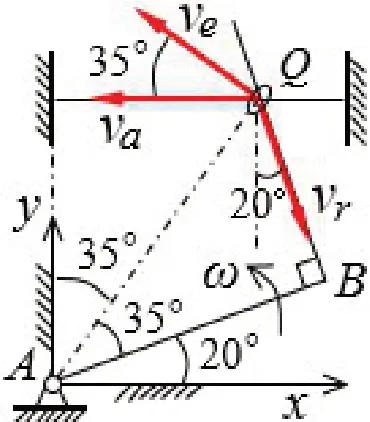
图7e
式(16)(17)同时代入式(18)并整理得:

其中摩擦系数f可以取任何值,例如f=0.1,f=0.2和f=0.3等时,式(19)都应该成立.这说明式(19)中所有含f项的和为零,即

式(20)代入式(19)并整理得:

上式实际上是摩擦系数f=0(即不存在摩擦力)时系统虚力方程的化简结果.实际上不论是否存在摩擦力,套环Q与弯杆ABC之间的速度关系都相同.
将式(20)(21)联立求解得:

至此,例7题已求解完毕.
作为比照,下面用运动学理论再次求解例7问题.
取套环Q为动点、弯杆ABC为动系(图7e),ve=ω·|AQ|=ω·|AB|/cos35°=1.220 m/s,ve⊥AQ,va=ve+vr,该式分别向水平、竖直方向投影得:

可见用运动学理论和用虚力原理,两者求解结果相同.但是例题7用运动学理论求解时比较抽象,很多学生尤其是初学者对牵连速度大小及方向不易接受,而用虚力原理求解时就完全避开了这些问题,解题思路及过程也很流畅.
4 结语
借助虚力原理,可以在不懂运动学理论的情况下,用静力学理论和动力学理论联合求解运动学中的速度问题.
对于定常约束运动学系统,例如已知A物体的速度(角速度或线速度),通过B,C,D等中间介质物体传递到E物体,求E物体的速度.利用虚力原理求解这类问题时,其统一解题模式为:对于A和E两个物体,在涉及角速度的物体上添加虚力偶,在涉及线速度的物体上添加虚力,并设想系统在虚力系作用下处于静止平衡状态;再以实位移替代虚位移,并把虚力想象为真实力,对系统列虚功原理方程(定常约束系统中实位移属于虚位移);然后用静力学力系平衡理论写出虚力系平衡方程,并与虚功原理方程联立求解,即可求出E物体的角速度或线速度.若引入滑动摩擦力,还能很直观地求出物体间的相对速度.
虚力原理与虚位移原理让静力学和运动学成为相互对偶、相辅相成的统一体,让静力学和运动学这两套原本看似毫不相干的理论有了内在联系性,也为求解运动学中速度问题提供了新思路、新方法.
