一类非均匀传输逆散射问题的混合交互关系研究
2021-09-06叶建国
叶建国
(喀什大学数学与统计学院,新疆喀什 844000)
0 引言
在逆散射问题中,交互关系刻画了散射场或远场的某种对称性(包括散射场与散射场、散射场与远场、远场与远场),通过交互关系,在数学上揭示了交换源(source)和接收器(receiver)的角色的合理性[1-2].混合交互关系在传输逆散射问题的理论研究中起着非常重要的作用,如在矿产资源的勘探、材料的无损检测、医学成像、雷达和声呐的探测等实际应用中,当目标障碍物或介质有一部分无法使用接收器搜集数据时,必须通过混合交互关系来简化问题[3-6].本文研究了一类带有传导边界条件的非均匀传输逆散射问题的混合交互关系,并给出问题对应的Green函数的远场G∞与全场u、穿透场v的交互关系刻画,为重构散射体做好理论准备.
1 问题的描述
设可穿透障碍物Ω∈ℝ3为开的单连通区域具有C2边界S.设障碍物Ω内外介质不一样且表面涂有阻抗率为λ>0 电导涂层,电场极化为TM 模式,当入射方向为d∈S2≔{x∈ℝ3:|x|=1}的入射平面波ui=eik0x·d遇到电介质时,在介质的边界∂Ω产生传导边界条件,记该非均匀可穿透散射问题的模型可用全场u和穿透场v的Helmholtz方程的传导边值问题描述为
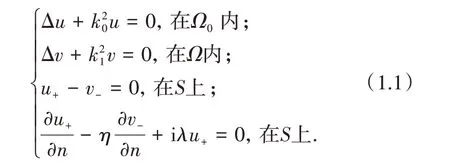
其中:波数kj>0(j=0,1),传输系数η>0 为Ω内外介质密度比,n 表示边界S的外单位法向量,i=全场u≔ui+us是给定的入射场ui和与之相应的散射场us之和,“±”表示x沿法线方向n从Ω的外(内)逼近边界S.此外,假设散射场us满足Sommerfeld衰减条件[1]
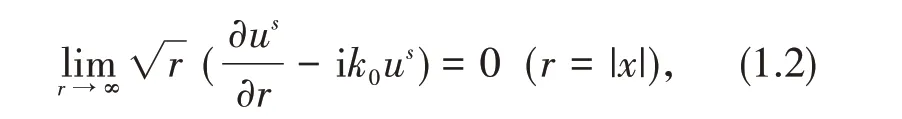
满足衰减条件(1.2)的Helmholtz 方程的解称为辐射解(radiating solution).当|x|→∞时,散射场us(x)有出射球面波(outgoing spherical wave)渐近表示
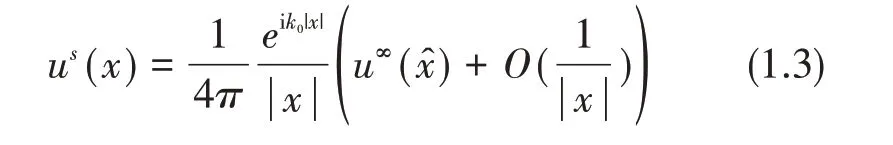
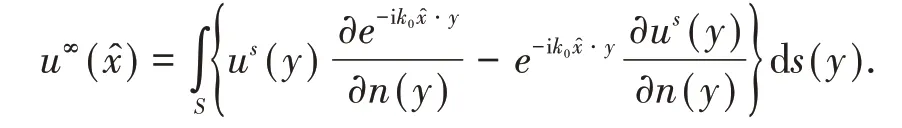
传导边值问题(1.1)—(1.2)的适定性邓霞等在文献[7]中应用积分方程的方法已经研究,文献[8]研究了该问题边值算子的非单射性.
2 混合交互关系
设G(x,y)是问题(1.1)—(1.2)对应的Green函数[8],则G(x,y)满足边值问题




综合(1)和(2),定理得证.
注2:由文献[9]—[11]可知,表示式(2.9)和(2.14)可以由经典的Green 表示公式中的基本解Φj(x,y)换成问题对应的Green 函数G得到.事实上,基本解Φj(x,y)是Helmholtz 方程的特殊Green函数.
