轨道交通诱发土体振动特性的现场测试研究
2021-09-06马险峰李金定张宝民
马险峰 ,李金定,何 斌,张宝民
(1.同济大学土木工程学院地下建筑与工程系,上海 200092;2.喀什大学土木工程学院,新疆喀什 844000)
许多国家大城市的轨道交通普遍很发达,这会导致振动公害普遍存在,因此对轨道交通诱发的振动问题进行研究和解决就显得尤为重要.对于环境振动在土层中的传播和衰减规律,国内外学者进行了大量的研究,主要采用了解析法、数值方法、现场实测及试验方法等.各方法在应用时并不是孤立的,而是联合运用,相互验证.
解析方法通过运用理论模型,结合数学以及力学中的理论对振动问题加以研究.Krylov 等[1]将高速轨道简化成Euler-bernoulli 梁,研究了列车振动的影;曹艳梅[2]研究了车、轨道和地基相互作用模型,该模型以列车动力学、轨道动力学以及地基土Green 函数为基础;Schillemans[3,4]采用了2D 有限元模型研究了铁路振动响应,并提出了减振措施,减小了地铁振动对古建筑的影响.但对于振动这种复杂的系统问题进行很多简化和假设,得到的解是不完全精确的.
随着振动测试传感器、数据处理方法和理论分析的完善,现场振动实测和试验方法显示了独有的优势.高峰与郭剑勇[5]采用模型试验的研究方法,设计不同工况,分析了双层隧道的响应问题.
试验结果表明,上下交会动载最不利,该工况下衬砌结构出现了应力集中现象;郑晓等[6]分析了现场实测的数据,认为地铁振动以中低频为主,竖直方向的振动分量大于水平方向的分量,并且沿地表的衰减速度也慢于水平分量.
本文在前人研究的基础上,采用现场实测的方法,分析了磁悬浮高架、地铁高架、城市高架桥及地面交通诱发的振动特性,并结合磁悬浮高架附近不同距离的测点垂向加速度信息分析振动的衰减规律.
1 现场测试方法
1.1 测试系统
本次现场测试采用的拾振器和放大器为中国地震局工程力学研究所制造的941B 型超低频拾振器和941 型16 线放大器.两者配接后加速度分辨率可达到5×10-6m/s2.采集仪器为美国国家仪器公司研发的NI9220 采集卡,采样率为100 kS/s/ch,通道数为48道,各通道同步采样.

图1 振动测试系统构成
1.2 测点布置
该测试场地位于上海硬X 射线隧道建设选址附近,紧邻磁悬浮、轨道交通16 号线、罗山路高架及罗山路地面交通等地.本次测点分别布置于附近四种交通处,即罗山路高架桥墩、磁悬浮高架桥墩和地铁线高架桥墩处,为了形成对比在地面交通附近也布置了测点.为了得到振动波在土中的衰减规律,在磁悬浮高架附近布置了不同距离的测点.
2 不同交通形式产生的振动波对比
2.1 时程分析
图2为四种交通方式的垂向时程图,地铁高架产生的振动在数值上最大,最大值约为0.12 m/s2.地面交通引起的振动在数值上最小,最小值约为0.003 m/s2.从波形上看,地面交通和罗山路高架产生的振动波比较杂乱,没有一定的规律性.磁悬浮在经过的时候会快速形成一个振动波,而地铁高架则会产生与地铁车厢相等的振动波个数.

图2 四种交通方式垂向时程图
图3为四种交通方式在横向、纵向和垂向的振动加速度箱型图.箱型图的方形箱体的上下代表振动加速度的四分之一和四分之三位数,也就是振动加速度数值的一半在箱体的范围内.箱型图的上下边缘代表振动加速度的最大与最小值.

图3 四种交通方式三向振动箱型图
图3(a)为地面交通引起的振动箱型图,可以看出三个方向的振动在数值上比较接近,振动最大值都在0.003 m/s2,垂向的振动幅度比其他两个方向略大点.振动箱型图的方形箱体大小正常,说明振动加速度的数值分布比较均匀.图3(b)为罗山路高架引起的振动箱型图,纵向加速度相较于横向和垂向小很多,横向产生的加速度最大.振动箱型图的方形箱体较小,说明振动的数值集中在比较小的区域内.图3(c)为磁悬浮高架产生的振动箱型图,可以看到纵向产生的加速度较大,而横向和垂向较为类似.振动箱型图的方形箱体的大小在四种交通状况下最小,说明磁悬浮的振动集中在很小区域内,数值较大的振动只有少部分.图3(d)为地铁高架产生的振动箱型图,可以看出数值上地铁高架相较于其他三个交通方式引起的振动最大,在纵向有比较大的振动加速度,而且箱型图的方形箱体大小正常,说明地铁高架引起的振动不集中在某一时刻.
2.2 频域分析
用Seismosignal 软件通过滤波和傅里叶变换可以得到加速度时程曲线对应的频域信息,这里截取0~100 Hz的频域曲线进行分析.为了将不同方向的频域图绘制到一幅图上,本文利用Origin软件的Savitzky-Golay (SG)法对数据进行平滑处理,因为分析的为比较大的幅值对应的频率范围,对幅值的精度没有很大的要求,所以这种处理方
式是符合分析需求的.图4 为SG 法平滑处理频域曲线的前后对比,可以看到曲线在平滑的同时保留了数值的相对大小信息,能够比较清晰地看出频域曲线在数值上几个较大的区域.

图4 Savitzky-Golay 法平滑处理
图5(a)为地面交通在三个方向平滑处理后的频域曲线图,可以看出三个方向的频率大都聚集在0~20 Hz 与50~80 Hz 区间内,0~20 Hz 对应的傅里叶幅值大于50~80 Hz的幅值,所以地面引起的大都为0~20 Hz 低频的振动.图5(b)为罗山路高架平滑处理后的频域曲线图,可以看出纵向的振动频率大部分聚集在0~10 Hz 和20~30 Hz区间内.横向振动频率62 Hz 与80 Hz 左右较明显,10~25 Hz 区间也有比较大的幅值,而垂向振动在0~90 Hz 内分布较均匀.图5(c)为磁悬浮高架平滑处理后的频域曲线图,可以看出三个方向振动频率都集中在65-85Hz 之间,90-100Hz 之间的振动也比较明显.图5(d)为地铁高架平滑处理后的频域曲线图,可以看出纵向和垂向的振动基本聚集在30~60 Hz 之间,而横向振动在40 Hz 与60 Hz处比较明显.

图5 四种交通方式三向频域图
3 振动波在土中的衰减规律
为了研究振动波在土体中传播及衰减规律,在磁悬浮高架附近布置了4 个测点,表1 为测点编号及其位置.
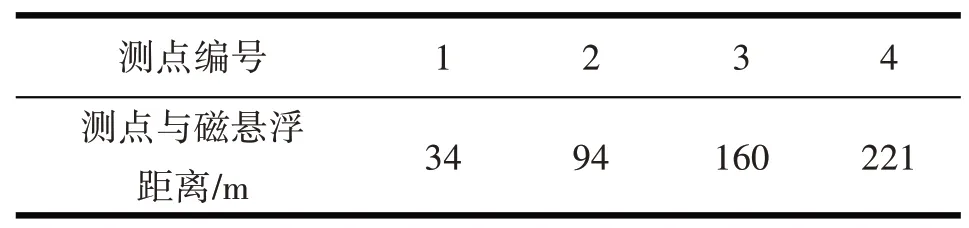
表1 测点布置位置
3.1 时程分析
图6为四个测点在垂向的振动加速度,从波形上看,距离磁悬浮高架最近的测点1的波形与磁悬浮高架桥墩较为类似,比较大的加速度集中在一小段时间范围内.随着距离的增加,加速度的数值在减少,而加速度数值在时程上的分布显得更加平均,在测点3 与测点4的波形图相对比较杂乱.图7为不同测点垂向时程箱型图,可见随着距离的增加,垂向振动衰减明显,在测点2的峰值大小衰减为测点1的一半左右,测点3的峰值大小又衰减为测点2的一半大小,测点4 与测点3 并没有很明显的区别.

图6 不同测点垂向时程图

图7 不同测点垂向时程箱型图
3.2 频域分析
图8 为不同测点在垂向的频域图,由图可见,随着距离的增加,大于20 Hz的振动衰减的速度比较快,而小于20 Hz的振动衰减速度较慢.测点3 与测点4的频域图基本上是重合的,可见当大于20 Hz的振动已经基本衰减的时候,依然有比较明显的小于20 Hz的低频波.

图8 不同测点垂向频域图
4 结语
本文通过现场测试,比对地面交通、罗山路高架、磁悬浮高架与地铁高架的振动数据,并比较磁悬浮附近不同距离的垂向振动数据,得出以下结论:
(1)比较四种交通方式的振动加速度数值可以发现,磁悬浮高架产生的振动波形相对于其他三种波形较为集中,地铁高架产生集中波形的数目大致与其车厢数目一致.罗山路高架与地面交通产生的波形类似,在数值上罗山路高架引起的振动较大,而地铁高架相较于其他三种交通方式会产生最大的振动加速度.地面交通产生的三个方向的加速度数值大致相等,罗山路高架会在纵向产生比较小的振动,而磁悬浮高架与地铁高架在纵向的加速度数值略大.
(2)比较四种交通方式的振动频域图可以发现,地面交通产生的振动大都聚集在0~20 Hz 区间内,磁悬浮高架产生的振动聚集在65~85Hz 区间内,地铁高架产生的振动聚集在30~60Hz 区间内,三个方向没有特别大的区别.罗山路高架的横向与垂向分布比较均匀,且会在60 Hz 左右产生比较大的幅值,纵向振动较小,只在25 Hz 左右会产生相较于另外两个方向比较明显的振动.
(3)比较不同距离的测点垂向加速度数据可以发现,振动随着距离发生衰减,并且小于20 Hz的振动衰减速度比大于20 Hz的振动小.当大于20 Hz的振动基本衰减结束时,依然有比较明显的低频振动.
