例析三角函数中ω的取值范围问题

江苏省海门中学 (226100) 姜敏华

在三角函数的图象与性质中，经常会遇到求ω的取值范围的问题，学生处理起来存在一定的困难，不知道如何等价转化问题的已知条件，造成求解范围不准确.本文将针对这一类型的问题确定条件的类型以及相应的求解策略.

1.零点个数确定

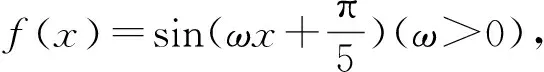
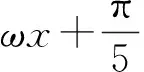
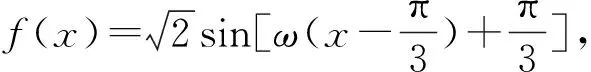
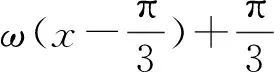
已知三角函数区间上的零点个数，需要根据区间的范围确定具体的零点进而确定ω的取值范围.类似的零点的个数还可以变为极值点个数，对称轴的条数，对称中心的个数等处理的方法相同.

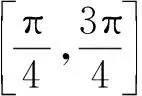
分析：采用整体思想，即在任意长度为定值的区间上，函数的零点至少有两个，至多3个零点，即找到必含有2个零点的区间长度，含有4个零点的最小区间长度.

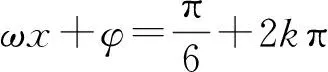
评注：对于区间长度为定值的动区间，若区间上至少含有k个零点，需要确定含有k个零点的区间长度，一般和周期相关，若在在区间至多含有k个零点，需要确定包含k+1个零点的区间长度的最小值.

2.区间上单调性已知

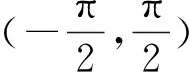
A.0<ω≤1 B.-1≤ω<0

C.ω≥0 D.ω≤-1

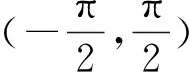
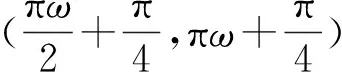
3.图象交点个数确定

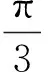
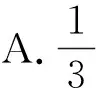
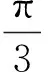
评注：三角函数图象经过平移之后与原函数图象完全重合，则移动的距离必为周期的整数倍.

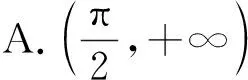
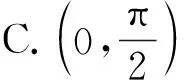
评注：此题可以看作平移后两个函数图象相交，给定3个相邻零点之间的关系，根据周期性，只需选择其中特殊的三个交点即可.进一步还可将问题进行变式，如△ABC是钝角角三角形，是等腰直角三角形，还可以考虑连续4个交点组成的四边形是菱形等.

结语：解决三角函数的图象问题关键是利用整体思想转化为正弦、余弦、正切函数的零点，对称轴、单调区间问题.抓住图象，运用代数方法，利用数形结合是解决此类问题的有效途径.