乌鲁木齐城镇办公建筑节能优化研究

韩飞，夏博，赵敬源，陶冶

（长安大学 建筑学院，陕西 西安 710064）

1 研究对象

我国城镇建成的公共建筑面积约占城镇民用建筑总面积的14%[1]，公共建筑的平均电耗约为全国居住建筑的2.5～3.5倍，因而在研究领域方面，本文选择公共建筑中最常用的2万m2以下城镇中小型办公建筑进行研究。乌鲁木齐地区属于严寒地区，能耗较高，目前，国内外对乌鲁木齐地区办公建筑能耗的研究较少[2]，因而在研究地域范围方面，本文以新疆乌鲁木齐地区城镇中小型办公建筑作为研究对象。

2 研究现状

2.1 能耗概况

乌鲁木齐公共建筑多为框架结构，以轻集料混凝土砌块作为内、外填充墙，外窗多采用铝合金窗或塑钢窗。屋顶保温多采用加气混凝土块；楼地面垫层多采用轻集料混凝土；外门多采用铝合金门[3]。

根据XJJ034—2017《公共建筑节能设计标准》中规定，乌鲁木齐为严寒C区。《乌鲁木齐国家机关办公建筑和大型公共建筑节能监测平台建设项目数据分析报告》中对乌鲁木齐24栋公共建筑能耗进行监测，其中21栋始建时间在2005年之前，没有按照GB50189—2019《公共建筑节能设计标准》进行设计，22栋为框架结构，23栋做了保温，监测的建筑具有相似性。统计可知，22栋办公建筑单位面积用热能耗平均值达到95.80 kW·h/（m2·a），单位面积总能耗平均值为123.66 kW·h/（m2·a）。

2.2 问题分析

目前，乌鲁木齐办公建筑能耗较高，需要改善和优化。围护结构是供暖能耗热损失占比最大的部分，不同部分的建筑围护结构性能差异性对建筑节能效果也带来了非常复杂的影响。建筑围护结构不同部位对建筑全年能耗影响的程度不一，而集中使用节能性能优良的建筑围护结构材料与结构形式又会大幅度增加节能投资，提高建设成本，降低了建筑节能的经济效益。同时，建筑围护结构之间也存在相互的影响，这种影响往往使围护结构的最佳效果方案并不是设计最低值，一味地使用高性能围护结构节能材料只会造成过度的成本增量。如何在保证建筑围护结构有效性的基础上，准确的定量评估建筑围护结构节能各因素的最优组合并具有经济的可行性，成为了建筑围护结构节能设计和投资决策的关键[4]。在此背景下节能设计中的多目标优化方法相较于传统的单因素优化方法，可以更加直观地反映围护结构各因子和建筑节能与经济影响的联系。该方法具有可体现各因素影响程度相关性的优点，有效减小对单因素的过度优化。对新疆乌鲁木齐办公建筑的多目标优化研究，将成为乌鲁木齐办公建筑节能和成本控制的关键。

3 新疆乌鲁木齐办公建筑多目标节能优化设计

3.1 多目标寻优方法的选择

建筑节能设计受多因素影响，当今学者开始使用多目标寻优的方式解决建筑节能各因素对能耗造成的影响。在建筑节能领域中比较常用的多目标寻优方法为转化法、正交实验法、人工神经网络分析等。正交试验设计法是目前最常用的建筑节能优化多目标寻优方式，通过建立各因素的垂直与水平正交表，以随机因子组合的方式进行试验，从而在试验中找出各因子的影响权重和最优解。正交试验设计在本质上是遗传算法中随机组合的部分随机性选取，正交试验设计法通过设计正交表[5]，使正交选取的因子相互随机组合，进行定向计算，其结果为遗传算法的初代个体的随机组合一代进化结果。遗传算法在试验次数上远超过正交试验设计法的实验次数，且因存在个体进化后的迭代计算，其计算结果要优于正交试验设计法产生的解。清华大学徐卫国教授在绿色建筑优化设计研宄中提出遗传算法被当今学者视作解决多目标优化问题的有效方法。因此，本文选用遗传算法的方式进行建筑节能设计多目标寻优，通过使用英国谢菲尔德大学开发的遗传算法工具箱[6]，以Matlab计算机语言编写，从而通过Matlab实现遗传算法，进行多目标寻优[7]。

3.2 基准模型建立

本文对算例城市乌鲁木齐所有建筑信息通过Python进行建筑信息数据爬取。对所有建筑大数据中的面积2万m2以内的办公建筑进行数据筛选，最终在169个办公建筑中得到42个符合要求的建筑信息，得到算例城市的办公建筑外轮廓多以长方形为主，建筑长度40～60 m，建筑进深14～18 m，建筑高度5层。结合实际调研，得到建筑体型系数应小于0.3；朝向在实际能耗计算时应考虑使用当地推荐的最佳朝向；通过对办公建筑平面进行优化，严寒地区建筑模型初步确定模型为40 m×14 m×18 m体块，单层面积为480 m2，层高3.6 m，5层，根据GB 50189—2019的规定，通过不同区域传热系数遴选材料与构造形式确定理论原型窗墙比，设定四侧墙体北方向窗墙比为0.35，东西方向窗墙比为0.10。南侧窗墙比根据规范外围护结构的热工性能参数依照节能标准设定。根据以上调研数据建立严寒办公建筑基准模型见图1。

图1 严寒地区办公建筑模型平面

3.3 多目标函数构建

对于公共建筑，由于GB 50189—2019中并未明确规定公共建筑设计建筑的耗热量指标，只需要设计建筑的相应数值满足相关标准的规范限值即认为达到公共建筑节能设计标准要求。因此，按照JGJ26—2018《严寒和寒冷地区居住建筑节能设计标准》确定建筑耗热量指标计算公式[8]：

由建筑耗热量公式qH与围护结构传热系数K之间的函数关系，记为Energy（K），本文研究针对建筑围护结构中的建筑外墙、建筑外窗、建筑屋面，其成本计算均为面积乘以单价。因此，本研究围护结构的成本公式为：

式中：Eqi——东、西、南、北方向外墙工程造价；

由式（2）和式（3）建立围护结构成本E与围护结构传热系数K之间的函数关系，记为Fcost（K）。基于遗传算法及建筑节能、热工等相关理论，选择外墙及外窗的传热系数作为优化变量[10]，建立子目标模型。根据式（1）～式（3），可分别建立建筑能耗及建筑围护结构成本关于外墙和外窗的传热系数的2个子目标函数为FEnergy（K）、Fcost（K）。在遗传算法中，这2个子目标函数视作2个平等个体进行迭代分析，因此子目标函数的权重分别各占50%，得出目标函数设为F（K），如式（4）所示：

3.4 优化参数选择及设置

对于建筑外围护结构中的屋面、外墙、外窗、门构成，同时在设计时外围护结构也会受到窗墙比的影响。因此，需要通过一种方式找出对能耗影响程度较大的因素作为主要优化方向，通过定量分析的方式进行优化参数的选择。通常情况下，门在办公建筑外围护结构中的面积比例较小，建筑门对外围护结构影响较小，因此本文选择屋面、外墙、外窗、窗墙比这4个外围护结构设计因素作定量分析，通过正交实验的方式对基准建筑在乌鲁木齐的气候条件下进行20组不同屋面传热系数、不同外墙传热系数、不同外窗传热系数、不同窗墙比的组合能耗模拟，找出基于乌鲁木齐气候条件下各因素的影响程度，确定寻优方向。

正交实验的计算结果中的极差R，表明因子对结果的影响程度[10]。在乌鲁木齐办公建筑模型中，对建筑能耗最大的影响因素为分别为：外墙（1049.33）＞外窗（1001.88）＞屋面（873.28）＞窗墙比（294.33）。由于窗墙比的R值与外墙、屋面、外窗的R值差距过大，因此在遗传算法中，重点针对外墙、外窗、屋面进行优化。

3.5 遗传算法求解过程

根据XJJ034—2017要求的建筑围护结构规范值，进行遗传适应度的约束。夏季室内计算温度26℃，冬季室内计算温度20℃，每人新风量30 m3/h，每间办公室2人，系统运营时间：周一～周五09：00～18：00及双休日关闭，计算关闭了照明能耗计算模块。根据文献调研情况及规范的推荐选择塑料窗框以及中空玻璃为窗的材料；墙体保温材料选择聚苯乙烯薄膜塑料板（EPS板）；建筑屋面保温材料选择EPS板[11]；建筑围护结构选取当前乌鲁木齐常见的典型构造做法作为基准，传热系数规范要求的区间就是遗传算法的约束值函数，由于乌鲁木齐的热工分区属于严寒C区，因此围护结构约束条件分别为：外墙传热系数K1≤0.43 W/（m2·K）；外窗传热系数K2≤2.3 W/（m2·K）；屋面传热系数K3为≤0.35 W/（m2·K）。

寻优计算将种群规模设置为100，总代数为100，停滞代数为100，采用软件模拟的可用最大默认参数进行计算。遗传算法的总代数可以理解为遗传到多少代时停止遗传的运行，停滞的代数则是当连续遗传迭代后适应度函数的加权平均值变化小于适应度函数值偏差时停止运算，其他默认设置不做修改[12]。

遗传算法工具运行后图形显示见图2。图中的圆形离散点为最佳适应度，即当前代数中最佳值；方形离散点为平均适应度，代表当前代数中所有参数的平均适应度能力，即当前代数中，建筑结构各参数与最佳值的差距。

图2 仿真模拟遗传最佳适应度值和平均适应度值

由图2可见，迭代停止在第100次，由于此时得出的最优值已经满足停止迭代的条件。该计算结果表明，在第100代中平均适应度值和最佳适应度值重合。进入遗传算法的停止计算流程，当种群个体间平均差异与期望值接近0时，说明计算的种群个体没有差异性，但系统仍进行计算，说明在约束值范围内可能存在更优的参数，该参数超出了建筑参数的设置值要求。乌鲁木齐的建筑节能仿真实验中最佳适应度值的下降速度还是相对稳定的，且最终下降到0附近，也就是说在设置的适应度函数最小时，达到了需求，故本次实验是有效的。随着时间的推移，个体间的平均距离不断减小，且期望值越来越接近于0，最后收敛于遗传代数第86代。该结果表明，在设置的遗传总代数100中，至86代达到了进化的极限，此时的各因子为最佳值，本代的参数即为最优的建筑围护结构最优传热系数。

3.6 遗传算法计算结果分析

遗传因子的适应度最大最小值如图3所示。

图3 遗传因子的适应度最大最小平均值

由图3可见，遗传因子的适应度最大最小平均值在不断进行类似于梯度下降的迭代且最终基本重合，代表遗传因子的适应度值已达到要求。在遗传算法中，当进化的前后代没有差异性时，代表计算结果进入稳态遗传，该结果表明，建筑围护结构的3个参数与增量成本在此时达到最优状态。后续10代的计算均以本代适应度为基准，未出现其他情况。

图4为对每一代贡献的父代及停止标准的水平。

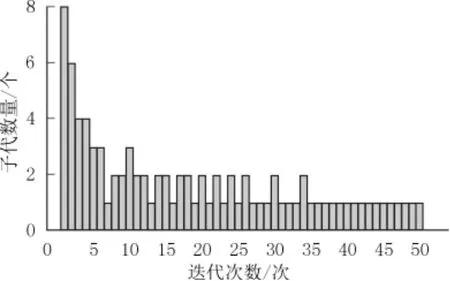
图4 每一代贡献的水平

由图4可以看到每一次选取的父代均继承了上一次的优点且逐渐趋近于稳定，而停止标准的水平也是随着迭代次数的增加而逐渐满足停止迭代的条件。

遗传因子结果输出如图5所示。

图5 遗传因子结果输出

根据图5的输出结果，经过100次迭代运算后建筑外墙、外窗、屋面最终的最优值为0.43、1.05、0.13。通过将建筑模型的围护结构设计参数调整为最优值，结果外墙外保温传热系数K=0.43 W/（m2·K），外窗传热系数K=1.05 W/（m2·K），建筑屋面外保温传热系数K=0.13 W/（m2·K），此时办公建筑模型的非供暖建筑耗电量为46.11 kW·h/（m2·a）。根据基准模型的平均耗电量57.84 kW·h/（m2·a）计算，其节能率达到了基准建筑的15%，在只进行围护结构优化的条件下，最高可使围护结构能耗负荷降低20.3%。

4 乌鲁木齐办公建筑遗传寻优结果推荐构造

4.1 外墙

根据遗传算法所得到乌鲁木齐当地适宜的外墙传热系数K=0.43 W/（m2·K），推荐适宜的构造形式。在原有模型的EPS外墙外保温层80 mm厚的情况下，传热系数已经到达寻优标准，因而在满足热工要求的同时，成本较低的构造形式为20 mm室内抹混合砂浆+200 mm加气混凝土砌块+20 mm水泥砂浆找平+80 mmEPS外墙保温（见表1）。

表1 外墙保温参数

4.2 外窗

根据遗传算法寻优结果，外窗传热系数K=1.0W/（m2·K）。目前使用的常规塑钢窗无法达到理论计算标准是产生建筑能耗提高的原因之一。模型原型使用的窗户为5白玻+12A+5白玻的双层中空玻璃窗。外窗热工参数见表2。

表2 外窗热工参数

由表2可知，随着中空玻璃层数的增加及玻璃材质的优化，外窗玻璃的传热系数降低[13]。根据遗传算法所得出的最优结论，外窗传热系数K值为1.05 W/（m2·K）时最优。根据目前外窗研究发展现状，传热系数达到1.05 W/（m2·K）的外窗国内少见且仅用于少量试验性建筑。因此对于乌鲁木齐地区既满足热工要求又较低成本的推荐构造形式为6白玻+12A+6Low-E或者6Sun-E+12A+6白玻的双层中空玻璃。

4.3 屋面

建筑屋面保温隔热性能不仅会影响顶层房间的能耗，而且会影响顶层房间室内热环境[14]。因此，屋顶应设置保温层。寻优结果表明，屋面外保温传热系数需要达到0.13 W/（m2·K），原有屋面保温厚度60 mm需要加厚到240 mm才可以满足。因此对于乌鲁木齐地区满足热工要求及最低成本的屋面构造推荐使用240 mmEPS外保温。

5 结论

研究表明，基于遗传算法的多目标寻优方法多用于理论性研究，可达到节能优化的设计需求，并有效控制设计成本。

在原有模型基础上，乌鲁木齐办公建筑围护结构的设计参数仍有优化空间，寻优结果为建筑外墙传热系数K=0.43 W/（m2·K），现有规范设计即可满足需要；建筑外窗传热系数K=1.05 W/（m2·K），根据目前外窗研究发展现状，推荐构造形式为6白玻+12A+6Low-E或者6Sun-E+12A+6白玻的双层中空玻璃；建筑屋面传热系数K=0.13 W/（m2·K），屋面保温厚度需达到240 mm。

经计算后，建筑模型的全年综合非供暖能耗下降至46.11 kW·h/（m2·a）。根据基准模型的平均耗电量57.84kW·h/（m2·a）计算，其节能率达到了基准建筑的20.3%，在只进行围护结构优化的条件下，最高可使围护结构能耗负荷降低20.3%。