具有恐惧效应的捕食者-食饵系统的全局动力学
2021-09-03韩梦洁刘俊利
韩梦洁,刘俊利
(西安工程大学 理学院,陕西 西安 710048)
捕食者-食饵的相互作用是生态学和进化生物学中的一个核心问题,许多研究者从不同的角度对其进行了广泛的研究.对捕食者-食饵系统的研究,通常假设捕食者通过直接捕杀猎物来改变食饵种群的数量.然而食饵在遇到捕食风险时会表现出不同的反捕食反应,包括栖息地的改变、觅食行为的改变、警惕性和生理等都会发生变化[1-4].因此,捕食系统中不但要考虑捕食者对食饵的直接捕杀行为还应该考虑捕食者对食饵的间接影响,即捕食者的出现引起食饵的恐惧效应.
Zanette等[5]对歌雀进行了实验研究,结果表明由于歌雀对捕食者的恐惧导致歌雀的繁殖率减少了40%.近年来,恐惧效应的影响已经得到了国内外学者的关注.数学模型是分析种群动力学行为的重要工具[6-7].2016年,Wang等[8]首次提出了一个具有恐惧效应的捕食模型,考虑了线性功能反应和Holling Ⅱ型功能反应,其研究结果表明对具有线性功能反应的模型,恐惧效应不影响其动力学行为,而对于具有Holling Ⅱ型功能反应的模型,增强恐惧水平有利于系统变得稳定.2017年,Wang等[9]建立了一个具有恐惧效应和对捕食者有适应性防御的捕食模型,数值分析表明恐惧效应的增强会导致系统出现周期解.Pal等[10]研究了一个Leslie-Gower捕食者-食饵模型,同时考虑了食饵的恐惧效应和捕食者之间的合作狩猎,研究表明相对于合作狩猎,恐惧效应的增强更有利于系统的稳定.文献[11-16]也从不同方面研究了具有恐惧效应的捕食模型.
功能反应的形式对模型的动力学行为有很大的影响,在本文中考虑Holling Ⅲ型功能反应,建立具有恐惧效应的捕食模型:

(1)

1 解的非负性和有界性及平衡点分析


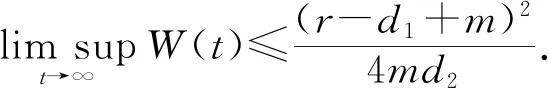
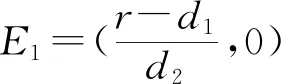
C0y2+C1y+C2=0.
(2)
式中:C0=kax*;C1=ax*+k(d1+d2x*)(1+b(x*)2);C2=(d1+d2x*-r)(1+b(x*)2).显然式(2)有一个正根y*,当且仅当C2<0时该条件等价于
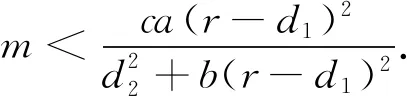
(3)

(4)
2 稳定性分析和Hopf分岔
2.1 平衡点的稳定性分析


(5)


证明 对于平衡点E0=(0,0),由式(5)得
(λ+d1-r)(λ+m)=0.
(6)
则式(6)有一个正根r-d1,一个负根-m,因此E0=(0,0)是不稳定的鞍点.


(7)
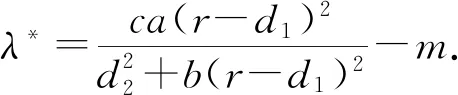

定理3 当下列条件之一成立时,E*=(x*,y*)局部渐近稳定:
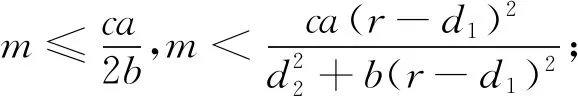
(8)
或者

(9)
当
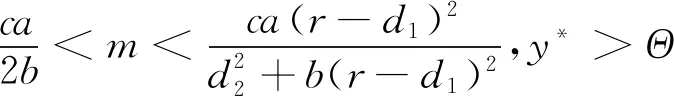
(10)
成立时,E*=(x*,y*)不稳定.
证明 正平衡点E*=(x*,y*)对应的雅克比矩阵为
相应的特征方程为
λ2-J11λ-J12J21=0.
(12)
显然det(JE*)=-J12J21>0,E*=(x*,y*)的稳定性由E*的迹tr(JE*)=J11决定.J11<0等价于

(13)

定理4讨论了正平衡点的全局稳定性.
定理4 当下列条件之一成立时,E*=(x*,y*)在第一象限内部全局渐近稳定:


(14)
或者

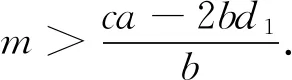
(15)
证明 由定理3的证明知只需要证明在第一象限内部没有周期解即可.首先对系统作替换,令dt=(1+ky)(1+bx2)dτ,则系统(1)变为
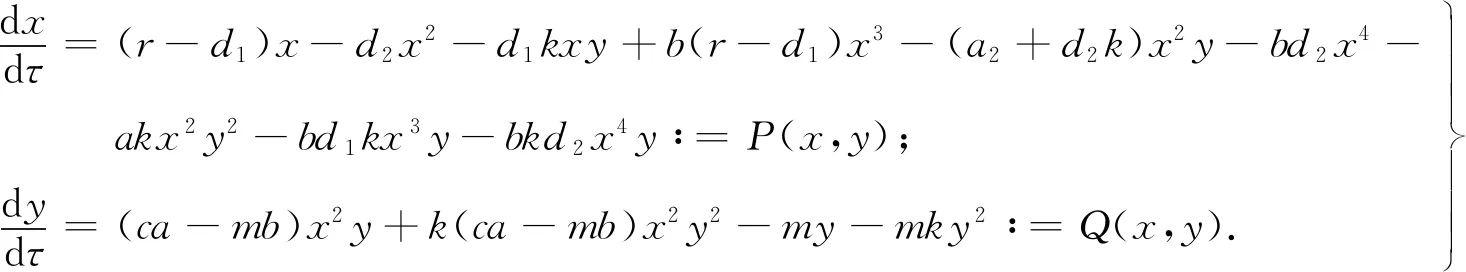
(16)

因此在定理4条件下,D<0.由Dulac-Bendixson定理[15]知,E*=(x*,y*)在第一象限内部全局渐近稳定.
2.2 Hopf分支
把系统(1)中的恐惧因子k作为分支参数,研究在正平衡点E*=(x*,y*)处出现Hopf分支的可能性.
定理5 当k=kh时,在E*=(x*,y*)附近出现Hopf分支的充分必要条件是

证明 在Hopf分支点,矩阵JE*应该有一对纯虚根,即J11=0,由此得:
由式(3)得:
因此特征方程(12)变为
λ2-J12(kh)J21(kh)=0.
(17)
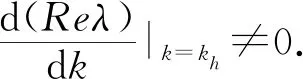
则定理结论成立.
下面来研究分支周期解的方向和稳定性.
首先,利用变换u=x-x*,v=y-y*,将系统(1)的平衡点E*=(x*,y*)移动到原点,则系统(1)变为

(18)
在(u,v)=(0,0)处进行泰勒展开到三次项,得:
(19)
式中:
忽略掉四次和高于四次的项,式(19)可以写成

(20)

令U=SZ,这里Z=(z1,z2)T,则式(20)变为

(21)
式(21)可以重新写成
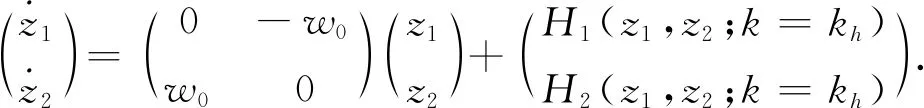
(22)
式中:
根据式(22)计算第一Lyapunov指数,得:

由文献[17],得定理6.
定理6 如果L<0,则Hopf分支为超临界的;如果L>0,则Hopf分支为亚临界的.
3 持久性
本节讨论系统(1)的持久性.
定理7 如果条件(3)成立,则存在ε>0,使得具有初值(x(0),y(0)),x(0)>0,y(0)>0的解(x(t),y(y))满足

证明 设X={(x,y)|x≥0,y≥0},X0={(x,y)∈X|x>0,y>0},∂X0=XX0,
易证X和X0是正不变的.∂X0为X中的闭集.由定理1知,系统(1)是点耗散的.定义
M∂={(x(0),y(0))|(x(t),y(t))∈∂X0,∀t≥0}.
由系统(1)知
M∂={(0,y)或(x,0)|x≥0,y≥0}.
定义系统(1)从初值(x(0),y(0))∈X的解的ω-极限集为ω(x(0),y(0)).记
Ω=∪{ω((x(0),y(0)))|(x(0),y(0))∈M∂}.
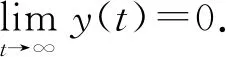
证明
Ws(E0)∩X0=∅,Ws(E1)∩X0=∅.
(24)
式中Ws(Ej),j=1,2为Ej的稳定流形.用反证法,假设Ws(E0)∩X0≠∅,那么存在一个解(x(t),y(t))∈X0,t≥0,使得

(25)
因为r>d1,因此存在充分小的η1>0使得

(26)
令t0>0充分大,使得当t>t0时有0

(27)
考虑方程(28)

(28)

因此Ws(E0)∩X0=∅.
假设Ws(E1)∩X0≠∅,那么存在一个解(x(t),y(t))∈X0,t≥0使得

(29)
由系统(1)得:

由定理1和定理7可得系统(1)的持久性.
4 数值模拟
本节将通过数值拟合来研究恐惧效应对系统动力学行为的影响.选取参数值
r=0.036,k=0.1,d1=0.01,d2=0.011,m=0.045,c=0.3,a=0.1,b=0.47,
则条件(15)成立,因此由定理4知正平衡点E*=(2.254 9,0.017 1)全局渐近稳定(见图1).

图1 正平衡点E*=(2.254 9,0.017 1)全局渐近稳定Fig.1 Globally asymptotically stable of the positive equilibrium E*=(2.254 9,0.017 1)
选取另外一组参数值
r=0.6,k=0.08,d1=0.01,d2=0.011,m=0.04,c=0.3,a=0.12,b=0.47,
在这一组参数下,在正平衡点附近系统(1)存在周期解(见图2).

图2 系统(1)出现周期震荡Fig.2 The periodic oscillations of system (1)
选取恐惧因子k作为分支参数,其他参数与图2中一样,得到系统(1)的分支图(见图3).

图3 食饵和捕食者关于恐惧因子k的分支Fig.3 Bifurcation diagrams of prey and predators with respect to fear factor k
由图3知,在恐惧因子增加的过程中,捕食者和食饵的数量由周期性的震荡到趋于稳定水平.当恐惧因子比较大时,恐惧效应不再对食饵的数量产生显著的影响,即在捕食者对食饵产生一定程度的恐惧后,由于对恐惧效应的习惯,恐惧效应在长期内将不会再影响食饵种群.
5 结 语
本文研究了带有恐惧效应的捕食者-食饵模型,采用了Holling III型的功能反应.对系统的平衡点作了全局稳定性分析,研究了分支周期解的方向及稳定性,对系统的持久性进行了讨论,并作了数值模拟来研究恐惧效应的影响.研究表明随着恐惧程度的增加,系统首先出现周期震荡,然后逐渐趋于稳定,捕食者数量会逐渐降低.因此恐惧效应的加入使得模型的动力学行为更加丰富.
