时滞切换LPV系统的鲁棒H∞控制
2021-09-03张秀华
张秀华,刘 薇
(东北大学 理学院,辽宁 沈阳 110819)
切换系统是混杂系统的一种,被广泛应用于实际生活.文献[1-2]对电力系统、机器人行走系统等进行了研究.文献[3-4]研究了一系列切换系统的稳定性.LPV系统(线性变参数系统)是一类重要的时变系统,最早在1988年由Shamma提出,在航天军事领域等有广泛应用[5].文献[5-6]主要针对时滞LPV系统,在稳定性、增益调度控制以及滤波等方面进行了研究.
时滞的存在会对系统的稳定性产生一定影响[7-8],在实际工程中,如电力系统、网络系统等,普遍存在的时滞会导致系统不稳定.当时滞存在于切换系统时,虽然系统的控制设计会变得复杂[9],但能够准确地描述实际系统.在研究切换时滞系统的稳定性[10-11]时,可以使用Lyapunov-Krasovskii函数的方法.
本文在文献[12-13]基础上研究了时变时滞情况下切换LPV系统的一系列问题,通过构造Lyapunov-Krasovskii函数,利用平均驻留时间[14-15]的方法得到使系统指数稳定且具有H∞性能准则的充分条件.由于该准则的系数矩阵与参数依赖Lyapunov函数矩阵之间的耦合,可以通过引用投影引理进行解耦;其次,由于该条件是无限维的,利用近似基函数和网格技术,能够将控制器的设计问题转化为求解有限维参数线性矩阵不等式的凸优化问题[16],这样更有利于数值的实现,最后通过仿真验证该方法的可行性.
1 问题描述
时变时滞切换LPV系统

(1)
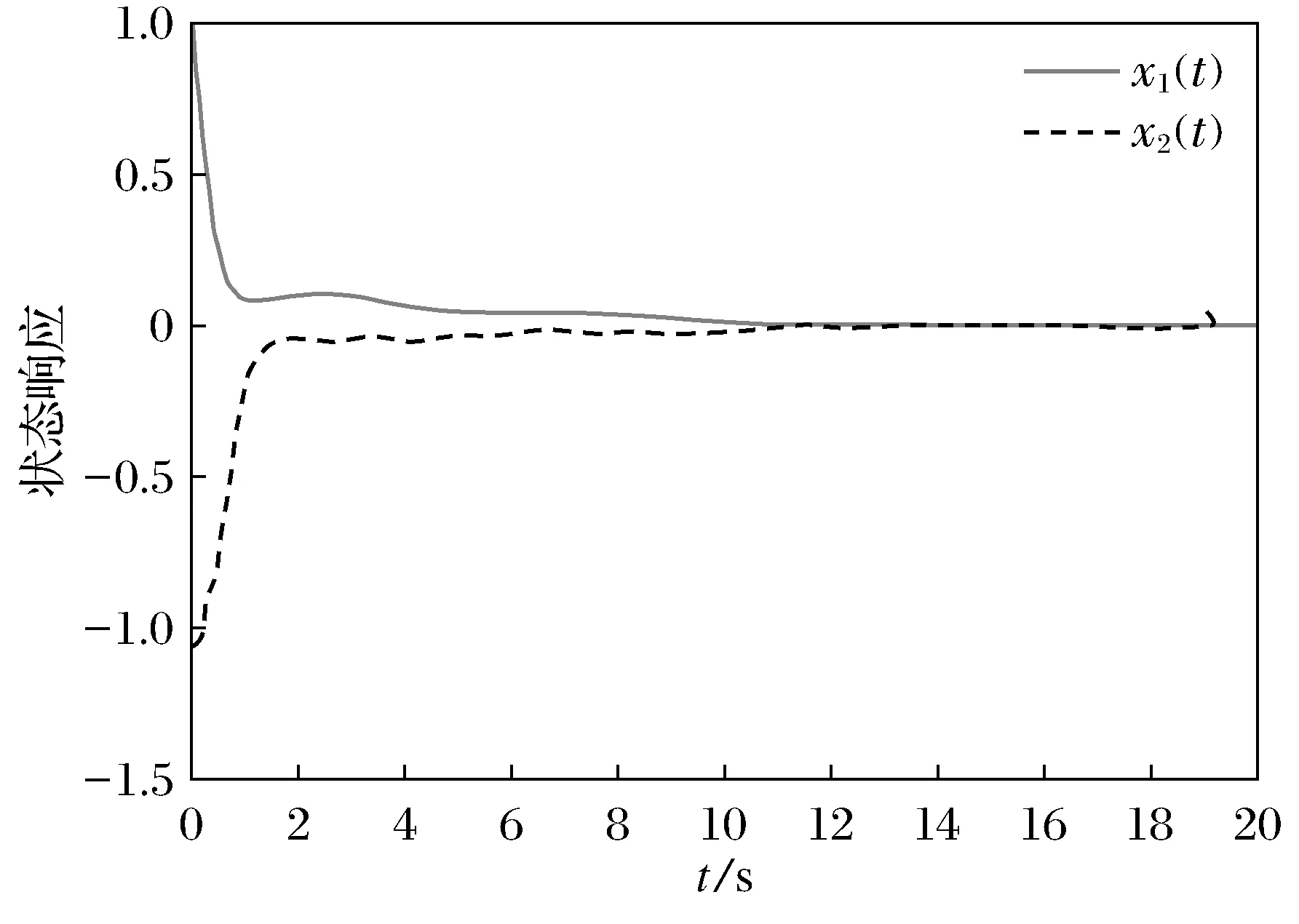
式中:x(t)∈n为状态变量,初始值为φ(θ);θ为初始时刻;u(t)∈r为输入变量;y(t)∈p为控制输出变量;ω(t)∈q为扰动输入;Aσ(t)(·),A1σ(t)(·),B1σ(t)(·),B2σ(t)(·),Cσ(t)(·),Dσ(t)(·)为时变参数ρ(t)的参数变化矩阵,为了书写方便,公式中将ρ(t)简写为ρ,ρ(t)=[ρ1(t),…,ρs(t)]T满足ρi(t)实时可测,且参数变化率σ(t):[0,∞)→i={1,2,…,N}是系统的切换信号;d(t)满足0 设计一个无记忆状态反馈控制器 u(t)=Kσ(t)(ρ)x(t),i=1,2,3,…,N, (2) 相应的闭环系统为 (3) 式中Kσ(t)(ρ)为待求的依赖于参数的反馈增益矩阵,其中: (4) 定义2[12]对于切换律σ(t),使得闭环系统的状态轨迹满足‖x(t)‖≤α‖x(t0)‖e-β(t-t0),α≥0,β≥0,t≥t0,则称系统是指数稳定的;若对于给定的标量γ>0,系统还满足‖y(t)‖2≤γ‖ω(t)‖2,则称闭环系统是指数稳定的,且具有H∞性能水平γ. 定理1 对于闭环系统,给定常数α>0,μ>1,γ>0,对于任意确定的σ(t),如果系统指数稳定,且具有H∞性能γ约束的充分条件是存在Pi(ρ),Qi,Zi,有式(5)成立, (5) Pi(ρ)≤μPj(ρ),Qi≤μQj,Zi≤μZj, (6) 且满足平均驻留时间 (7) 证明 选取第i个子系统的Lyapunov函数为V=V1+V2+V3,且 当ω(t)=0时, 当系统运行在[tk,tk+1)时, 由Schur引理,Π与式(5)是等价的. 当系统运行在时间域[t0,t1),…,[tn-1,tn)且初始时间为0时,即x(t0)=0,考虑: 由定理1可知:J≤0. 这个结果与参考文献[12]相比较,引入了时变时滞,增加了一定的难度,提供了理论依据,便于实际系统的应用. 定理2 在定理1的基础上,对式(5)进行解耦,存在矩阵Ui使得式(6)以及式(8)的矩阵不等式成立: (8) 其中Ui是连续可微的和正定对称的. 证明 由矩阵变换,式(8)等价于 所以由投影条件产生 运用Schur补引理,由式(10)推出式(5),式(5)包含式(8),因此式(6)~(8)能够使该定理成立. (11) (12) (13) (14) 并运用网格技术进行求解. 推论最优扰动衰减水平γ求解如下: minγsubject to(11),(12),(14). (15) 考虑形如式(1)的系统,参数矩阵中子系统1为 子系统2为 其中:ρ1=sin(t),ρ2=|cos(t)|为时变参数,满足ρ1(t)∈[-1,1],ρ2(t)∈[-1,1].选取近似基函数f1(ρ)=1,f2(ρ)=ρ1(t),f3(ρ)=ρ2(t),有 构造如图1的一个随机切换信号,干扰信号为ω(t)=2e-0.6tsin(0.03πt),取x(0)=[-1,1],平均驻留时间满足τa=2,由图2可以看出,该闭环系统是稳定的. 图1 系统模态Fig.1 System mode 图2 状态响应Fig.2 State response 在定理1中,通过设计无记忆状态反馈控制器,使系统达到稳定并具有H∞性能γ;但由于满足定理1的矩阵存在耦合,因此,在定理2中根据投影引理及零空间矩阵对定理1得到的矩阵进行解耦;在此基础上,设计状态反馈控制器得到定理3;由于参数具有依赖性,选取适当的近似基函数,并运用网格技术求解控制器以及最优扰动衰减水平γ. 本文运用平均驻留时间的方法对时变时滞切换LPV系统的稳定性进行分析,得到了满足闭环系统稳定和具有干扰抑制水平γ的充分条件,并求解了满足该条件的控制器以及最优扰动水平γ,最后通过仿真验证了其有效性.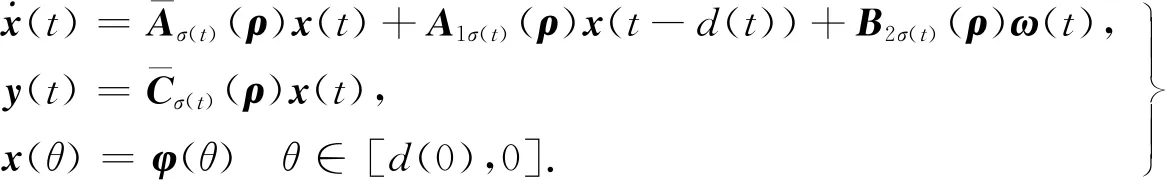
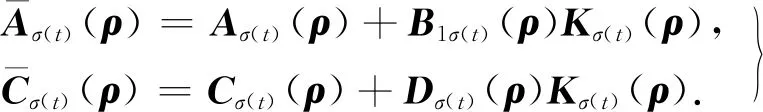
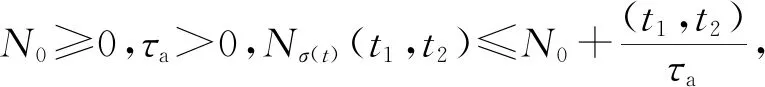
2 指数稳定及H∞性能准则
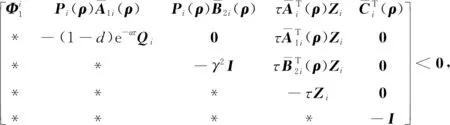
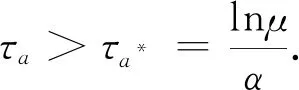

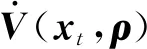

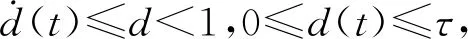
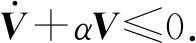

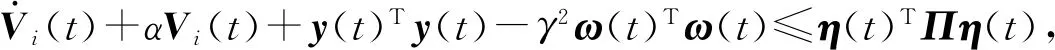
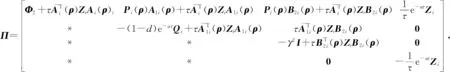
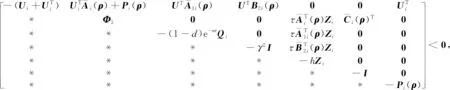
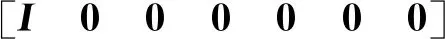
3 H∞状态反馈控制器
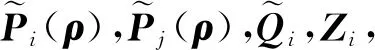

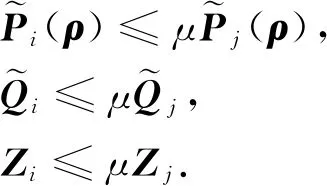

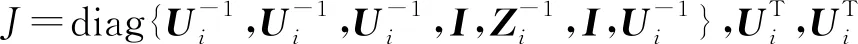

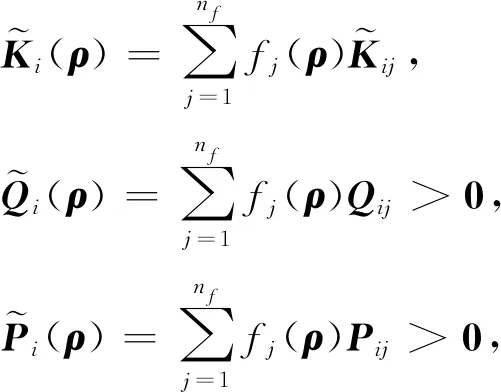
4 算例仿真


5 结 论
