加权网络中改进的谣言传播模型

姜 雪,皇倩倩

(沈阳大学 a.信息工程学院,b.装备制造综合自动化重点实验室,辽宁 沈阳 110044)

在21世纪互联网信息大爆炸时代,谣言越来越容易借助于互联网自媒体等网络传播[1],这对社会以及个人造成了一定的危害,所以关于网络谣言传播的学术研究越来越多.谣言作为社会活动的产物,只要存在人类的社会活动,就不可避免.针对谣言的理论阐述有多种[2-3],早在1965年,Daley和Kendall以数学方式形式化了经典的DK谣言传播模型[4],Huo等[5]对经典的SIR模型进行补充,考虑自我成长机制和不可分辨程度,建立了IWSR谣言传播模型.顾秋阳等[6]以经典SIR模型为基础,加入移动社交网络用户数量等影响因子进行优化,并结合传播动力学理论构建了移动社交网络谣言传播的参与群体动态演化模型.2016年朱张祥等[7]将谣言受众对象扩展为无知者、知晓者、信任者、传播者、暂时免疫和永久免疫,同时考虑正向社会加强效应建立模型,并在无标度网络下研究.Wang等[8]研究了社交网络中信息互动模式及传播特点,在经典SIR模型上通过线性回归分析研究了虚假信息在社交网络上的传播过程及其对社会造成的危害.朱霖河等[9]在社交网络谣言传播模型中,考虑到辟谣机制和时滞效应对网络谣言传播的影响,建立了一种基于辟谣机制和时滞效应的SIR谣言传播模型.Zhu等[10]研究了在同质网络和异质网络中谣言传播模型的动态分析与控制策略,Yu等[11]研究了在多语言环境下谣言的传播与控制,并且证明了当谣言爆发后各官方机构借助各社交平台发布信息,使民众以最快速最便捷的方式获得权威的官方信息,进而能辨别虚假信息,不再相信谣言并停止传播谣言是当前辟谣的一种重要的方式[12-14].研究者还发现社交网络中个体对谣言态度的选择总是与多数个体的选择趋于一致,即“从众效应”[15].虽然已经有大量的学者在不同状态下研究过谣言传播模型以及谣言在不同状态下的传播过程[16],但始终没有人考虑个人的社会影响力,以及人与人之间的亲疏关系,即加权网络下考虑惩罚因子时谣言的传播过程[17-18].本文将研究加权网络下改进的谣言传播模型.

1 模型的建立

文献[16]通过引入惩罚因子,建立了具有惩罚因子的谣言传播模型.本文在此基础上,考虑不同权重情况的谣言传播模型.假设谣言的总数为N,模型中节点i与节点j之间边的权值为wij(0≤wij<∞),在整个谣言传播的系统中,只对无知者转变为传谣者概率α′加权,类比现实生活,每个在社会中的实体个人由于本身的受教育程度,个人社会影响力,以及我们在事件发生后的话语权,影响力是不同的.回归本系统,无知者对信息的接受程度以及转变成为传谣者的程度也会存在这种现象,所以只对α′进行讨论,则可建立以下在加权网络下改进的谣言传播模型:

式中α′为无知者转变为谣言传播者的概率.在加权网络中,若节点i与节点j之间的权重为wij,则无知节点i受传播节点j影响转变为传谣者的概率可记为αij,且α′=αij,则进行如下定义:

(4)

在α=θα0(1-e-wij)中,α0为谣言爆发时谣言的初始传播概率.其中θ=[1,∞),且θ(1-e-wij)∈[0,θ)为谣言传播概率变化的因子,其数值的变化率随两节点间的权重改变而改变.则在传播系统中考虑一个独立节点在遇到谣言时,在t时,若节点与其邻居节点不考虑传播概率为1时,那么无知者在加权网络下转变为传谣者的概率为

p=1-[1-θα0(1-e-wij1)][1-θα0(1-e-wij2)][1-θα0(1-e-wij3)]…[1-θα0(1-e-wijn)].

(5)

将惩罚因子引入谣言传播模型,建立以下改进的模型:

式中:〈k〉为网络的平均度;η为对传谣者的惩罚率;λ为对无知者的惩罚率.

其传播过程示意图如图1.

2 谣言传播过程的稳态分析

假设在谣言传播初期的初始条件下无知者sk(0)=s(0),为了不失一般性,认为初始状态下s(0)≈1.直接对式(6)两边进行积分得:

sk(t)=e-(α+λ)〈k〉φ(t).

(9)

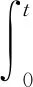
对式(7)进行积分得:

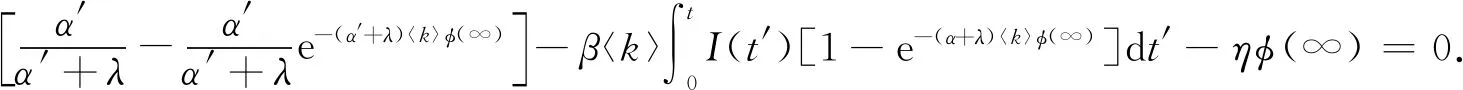
(11)

通过数学变化得:

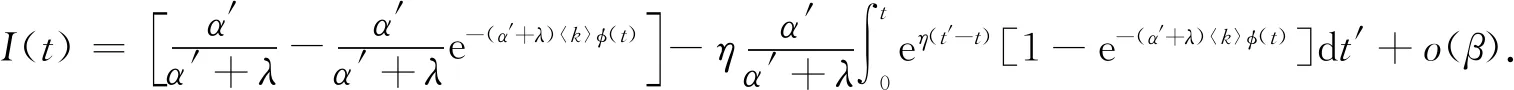
(12)

当接近传播阈值时φ(t)和φ(∞)非常小,设φ(t)=φ(∞)μ(t),其中μ(t)为正定有限函数,在φ(∞)处对式(12)进行泰勒展开得:

把式(13)插入式(11),并在φ(∞)处指数展开得:

通过数学变化得:

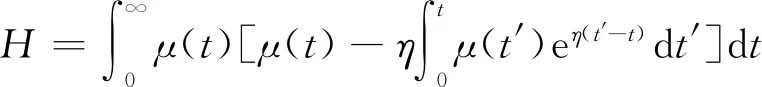
(16)

从式(16)可以看出,谣言传播依赖于α′、η;同理,验证式(8)可得谣言传播依赖于α′、λ;由此可得r值.

3 实验结果分析

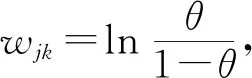
设置初始参数α=0.8(在这种状态下,默认权值为1),β=0.2,η=0.4,λ取4个不同值,和确定权重后参数α′=0.552,β=0.2,η=0.4,λ取4个不同值时,研究传谣者在其他参数不变情况下,权重大小以及对易感者惩罚力度不同时传谣者密度的变化.得到如图2所示的结果.设定max{i(t)}为谣言感染密度的最大值,由图2(a)和图2(b)可以看出权值越大在谣言传播系统中的影响力和max{i(t)}的峰值就越大,且谣言到达峰值的时间更短.

图2 权值不同,当惩罚因子λ取不同值时i(传谣者)的变化曲线Fig.2 When the weight is different and the penalty factor λ takes different values,the change curve of i (the rumormonger)

接下来讨论η对谣言传播的影响.设参数α=0.8,β=0.2,λ=0.4,η取4个不同值,和确定权重后参数α′=0.552,β=0.2,λ=0.4,η取4个不同值时,研究传谣者在其他参数不变情况下,权重大小以及对传谣者惩罚力度不同时传谣者密度的变化.得到如图3所示的结果.从图3中可以看出,无论权值为何,max{i(t)}都随着惩罚因子η的增大而减小.现在对比图2(a)、图3(a)可知,分别将易感者和传谣者惩罚因子λ、η从0.2增加到0.4时,图2(a)max{i(t)}峰值始终低于图3(a)的峰值,则通过对比图2(a)、图3(a)可以得到对谣言传播者同等比例增大惩罚因子η的值可以更有效地降低整个模型中max{i(t)}的峰值;同样的,对比图2(b)、图3(b)可知分别将易感者和传谣者惩罚因子λ、η从0.2增加到0.8时,增加传谣者惩罚因子比增加易感者惩罚因子时max{i(t)}峰值降低幅度大.从这些结论中可以得到如下结论:在谣言传播过程中,若想更好地降低谣言的最大影响力,降低谣言对社会的危害程度,增大对谣言传播者的惩罚比对易感者进行惩罚更有效.

图3 权值不同,惩罚因子η取不同值时i(传谣者)变化Fig.3 When the weight is different and the penalty factor η takes different values,the change curve of i (the rumormonger)

现在设置参数α=0.8,β=0.2,η=0.4,λ取4个不同值,和确定权重后参数α′=0.552,β=0.2,η=0.4,λ取4个不同值时,研究免疫者在其他参数不变情况下,权重大小以及对易感者惩罚力度不同时免疫者密度的变化情况.得到如图4所示的情况,从图4(a)、图4(b)可以看出,权值越大,在谣言传播系统中的影响力越大,从而影响整个系统中无知者s,谣言感染者i,免疫者r的密度.无论权值大小如何,在增大易感者惩罚因子λ时都会使最终免疫者到达的峰值max{r(t)}降低,即惩罚因子作用下使整个系统中谣言感染者降低,从而使免疫者达到的峰值降低.同理,在其他参数值不变的情况下改变惩罚因子η值会得到相似结果.即在网络中对传谣者进行惩罚也可有效降低谣言传播的最终数量.

图4 权值不同,惩罚因子λ取不同值时r(免疫者)变化Fig.4 When the weight is different and the penalty factor λ takes different values,the change curve of r (the immunized person)

4 结 论

本文研究了加权网络中改进的谣言传播模型,通过仿真验证了加权网络中权值对整个谣言传播系统的影响情况.仿真实验表明无论权值大小如何随着惩罚因子增加,系统中传播者的密度都会越来越小.