移动机器人最小化snap与A*的联合轨迹优化

韩晓微,刘宏宇,石泽亮,刘 晓

(沈阳大学 a.科技创新研究院,b.信息工程学院,辽宁 沈阳 110041)

路径规划是移动机器人技术研究中的重要组成部分[1],其目的是为移动机器人寻找一条从起点到终点的安全(无碰撞)、高效(最短距离或最短时间)的最优或接近最优的路径[2].

常用的路径规划算法有蚁群算法、粒子群算法、模拟退火算法和神经网络等[2].目前对路径规划算法的研究主要基于真实环境的栅格分解描述,把机器人的运动环境分解成许多简单的栅格,根据是否被障碍物占据来进行状态描述[3].Dijkstra算法解决的是有向图中从一个节点到其他节点的最短路径问题.以起点为中心,逐步向周围相邻节点拓展,被拓展的点都是到该点的最短路径,直到达到目标点[4].该方法在地图较小时可以使用,随着地图的增大计算量也会急剧增长[5].针对此问题提出的A*算法融合了Dijkstra算法及贪心算法思想,通过计算启发函数来评估当前节点到下一节点的代价大小来寻找一条最优路径.此算法应用较为灵活,但当起点与终点之间的距离较长时,A*算法评估代价时会计算大量重复数据,降低搜索效率[6].

2017年Charri等设计了松弛A*算法,其执行时间大大减少,增大了约束性复杂度,松弛A*能成为最佳路径规划器是因为其在度量之间提供了良好的权衡[7].石征锦等[8]在启发函数中加入余弦相似性和方向信息,再做归一化处理,改进A*算法.辛煜等[9]成功扩大搜索邻域,重新定义中心节点位置,在每个节点周围扩大无限的可搜索邻域,快速实现无碰撞的路径规划.王殿君[10]针对路径规划数据包含规划点的冗余坐标和移动机器人无法在拐点处调整姿态的问题,提出能够计算拐点、发现最优旋转角度的A*路径规划改进算法.王洪斌等[11]通过引入二次A*算法减少路径轨迹冗余点,缩短长度并采用自适应圆弧与加权障碍步长调节优化算法,利用预瞄偏差角度追踪移动目标点,有效提升路径规划效率.

本文充分分析了目前已有的路径规划算法,针对移动机器人路径规划中使用A*算法时存在的折线多、转折角度大等无法实际应用的问题,提出一种采用MS优化A*算法的路径规划思路,将折线路径变为平滑曲线路径,解决了该算法规划的路径不满足移动机器人物理特性而无法较好实际应用的问题,保证路径规划算法的优越性和可行性.

1 A*算法

A*算法是由斯坦福大学教授Nils Nilsson于1968年提出的一种基于图的启发式搜索算法.该算法旨在保留Dijkstra算法路径搜索全局最优性的同时引入代价函数,用于节点动态筛选的遍历定量描述[12-13].由于其具有绝对路径搜索可靠性且大幅提升算法实时性的优势,满足实际工程对自主移动机器人的考量,因此被作为基础搜索算法得到了广泛的学习改进与实践应用.

对真实环境完成栅格地图构建之后,起点、终点、障碍物区域以及可行区域均隶属于同一八连通结构树,其简述路网节点拓扑模型如图1所示.

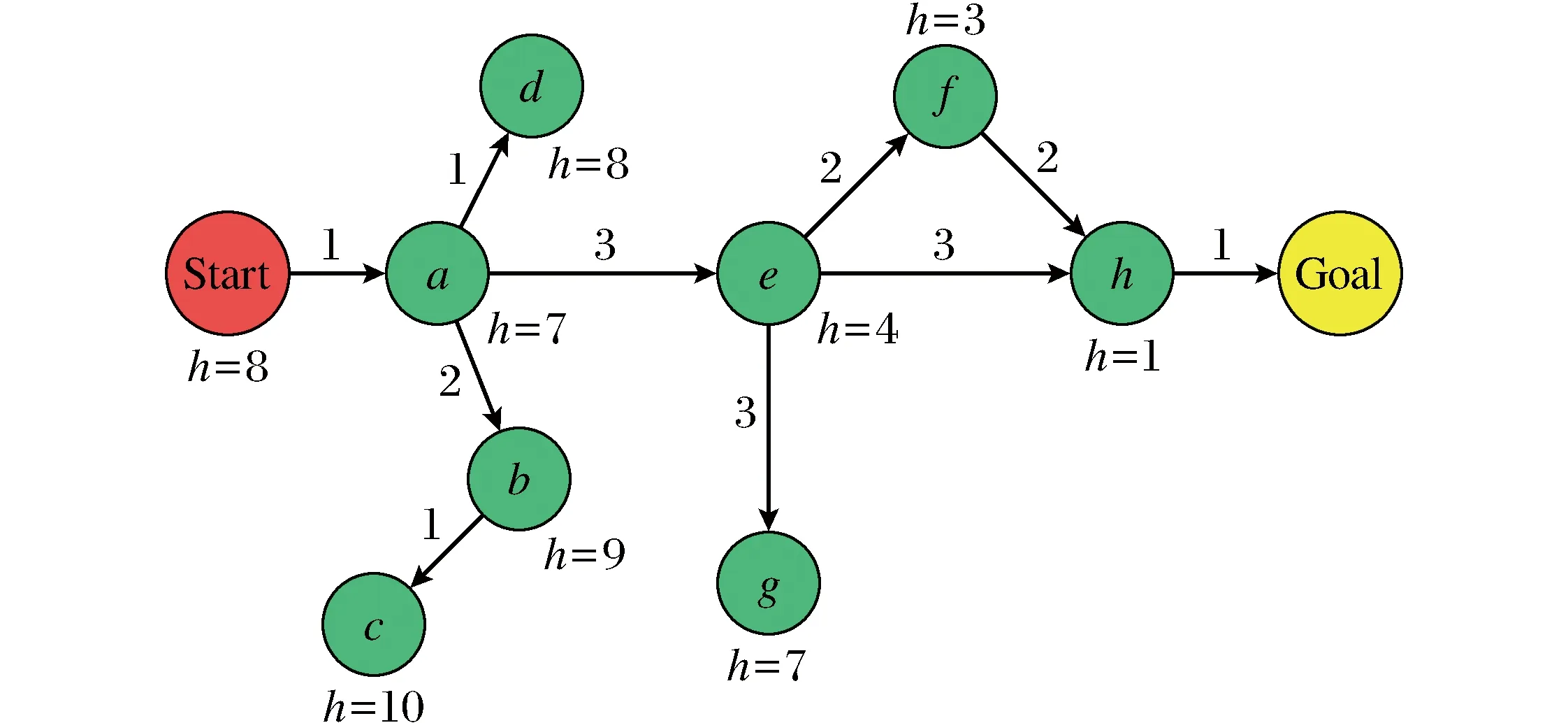
图1 A*算法节点Fig.1 Nodes for A* algorithm

将搜索区域内所有节点以全局坐标系下二维坐标表示,此时地图中所有节点均连接在同一结构图中,同时对起点、终点、障碍物及可行区域进行标注,则路径搜索问题转化成在图中找到一支满足代价最小要求的结构树,且从终点子节点向前回溯父节点直至起点节点即可找到所需静态最短路径.构造代价函数建立搜索准则,其函数一般形式如式(1)所示.

f(n)=g(n)+h(n).

(1)

式中f(n)是从自定义起点到自定义终点的代价函数,g(n)是从起点到中间节点n已产生的累计代价函数,h(n)表示从中间节点n到终点还需产生的累计估计代价.

算法执行流程是:首先使用一个优先级队列对搜索树里的所有节点进行排序.开始时,每个节点的值都是未知的.当扩展到该节点的时候再根据事先规定的欧式距离或者马氏距离计算得到,同样优先级队列一开始时是空的,初始化时只放入起始节点,并且把累计代价设为零,其他节点的累计代价设为无穷大,进行迭代.首先从搜索树里弹出最小的节点,将该节点标记为已经扩展的点以后不再访问,同时判断是不是终点以及循环是否结束.接着扩展当前节点的邻节点,对于未被扩展过的节点,首先判断是否为新发现的点,如果是计算它的值,将其放入优先级队列;如果该节点之前就被别的点当作邻节点发现过,即现在已经存在于优先级队列中,则看g(n)的值能否通过当前节点获得一个更小的值,如果能获得则对其值进行更新.对于A*而言,更新g(n)值的同时还需要将f(n)的值重新计算一遍.此时优先级队列会形成新的排序.Dijkstra算法与A*算法搜索结果如图2所示(见封3).

图2中绿色点为起点、黄色点为终点、黑色点为障碍物区域、红色格子表示算法搜索过程中需要拓展的栅格、深蓝色为下一步待拓展位置、青色为算法最终搜索出的全局最优路径.

从理论上分析,A*算法在节省计算时间方面是最优的,但随着搜索空间的扩大,节点数目的增加,搜索时间也会增加,且其应用受到室内环境图大小的限制,也存在客观因素的不合理性,例如没有考虑移动小车自身体积大小及物理学状态、机器人步长、障碍物形态等多约束条件.

2 基于最小化snap的轨迹优化算法

移动机器人运动规划问题分为前端路径规划和后端轨迹优化,由于路径搜索通常不考虑机器人动力学模型,机器人难以执行,因此需要引入轨迹优化.根据微分平坦理论可以将高维的状态空间转化为低维的平坦的输出空间表示[14].snap是加速度的二阶导数,将其作为被控量处理相当于最小化角加速度即动力的微分,使得动力变化尽可能的平缓,达到节省能量的效果.

2.1 算法框架

分析A*算法得到路径点步骤并针对其难以应用于移动机器人上的不足设计了本文算法,图3是本文算法框架及流程图.输入轨迹的起点和终点,经A*算法搜索得到中间路径点,通过本文算法的轨迹优化处理后得到一条满足机器人动力学约束的最优轨迹.

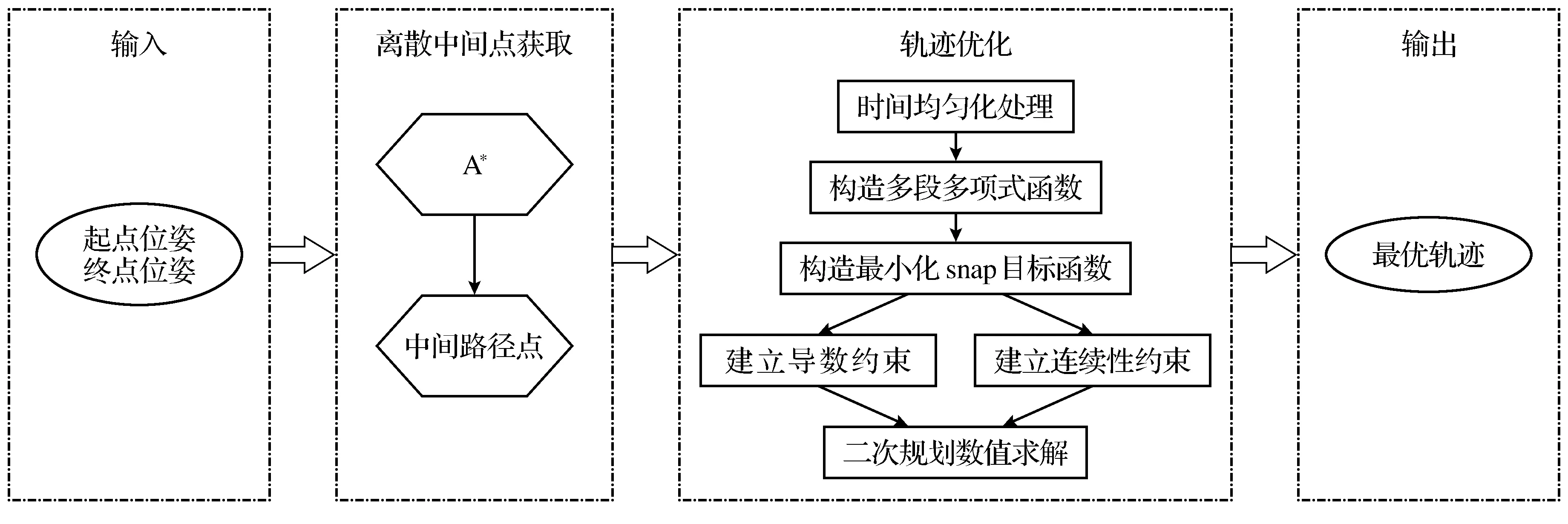
(a)算法框架

从图中可以看出,在A*算法得到离散路径点后,算法在每两点间做时间均匀化处理,在对每小段路径分别优化之后构造多段多项式函数用于描述整条轨迹.对每小段轨迹建立最小化snap目标函数并根据机器人起点、终点状态空间参数建立导数约束;根据机器人到达两段轨迹连接节点时状态空间值保持不变建立连续性约束.最后将问题转化为二次规划问题,由规划器进行数值求解,得到轨迹参数向量即得到最优轨迹.

2.2 时间均匀化处理

由于A*搜索得到的路径点较稀疏,容易造成轨迹不平滑,为了更好地控制机器人运动,需要将稀疏的路径点变成平滑的曲线或者稠密的轨迹.在两点间做时间均匀化处理,用多段多项式表示轨迹.选用多项式的原因在于其计算简便且可以快速得到轨迹中点的状态空间信息,控制器易于对机器人控制,具有良好的实时性,其对应轨迹表达式如式(2)所示.

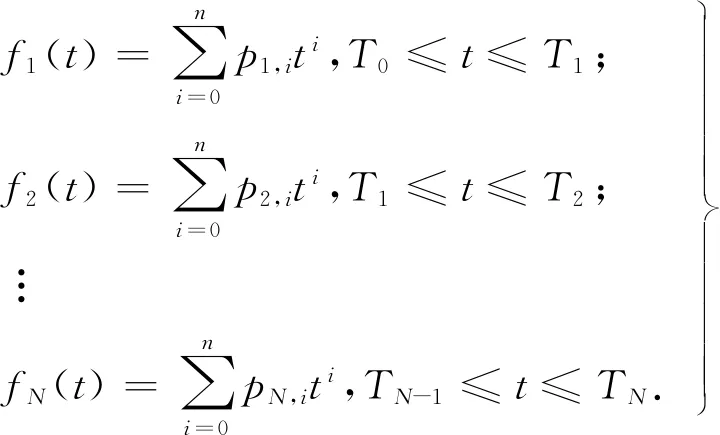
(2)

式中,整个轨迹f(t)由N段轨迹f1(t),f2(t),…,fN(t)拼接组成;每段轨迹由同阶的n阶多项式表示;每段轨迹的时间间隔相同且将整个轨迹时间均分为N份[15].

图4(a)呈现了3组A*搜索结果,图4(b)为相应处理细节显示表达(见封3).红色◆表示机器人经过的路径点,连线表示A*生成的全局最优路径,绿色矩形框表示按照时间间隔对其进行均匀化分割处理.

2.3 最小化snap目标函数

为了满足机器人的理运行特性,使其更加符合运动模型,本文对A*规划结果进行相应处理,分别对每一段轨迹做最小化snap的最优化处理,式(3)是轨迹经最小化snap处理后的代数形式表达式.

f(4)(t)=∑i(i-1)(i-2)(i-3)ti-4pi.

(3)

为防止正负号相消的情况,选择取函数二范数做最小化优化,式(4)是二范数表达式.

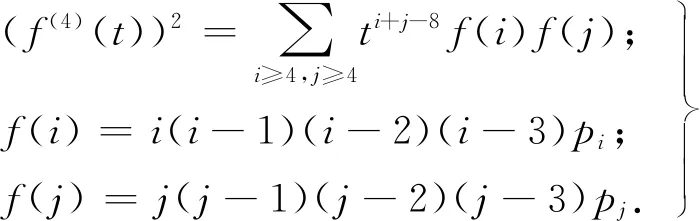
(4)

式(5)是目标函数表达式,

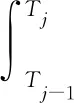
(5)

将式(5)以矩阵形式展开可得式(6),

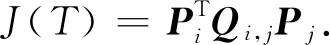
(6)

将式(6)简化为二次型形式表示如式(7),

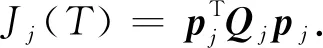
(7)

每段轨迹叠加可得最终整个优化轨迹,如式(8),

J(T)=pTQp.

(8)

2.4 约束条件建立

为了使机器人能够很好地执行优化算法,本文针对实际问题选用导数约束和连续性约束2类模型.

导数约束包括起点和终点的位置、速度、加速度的边界条件以及中间点的位置坐标[16].连续性约束为保证每段轨迹一定经过相应的连接点,虽然中间段轨迹不限制到达中间点时的速度或加速度,但是需要前后相接的2段到达同一点的速度和加速度值相同[17].图5为约束条件建立示意图.

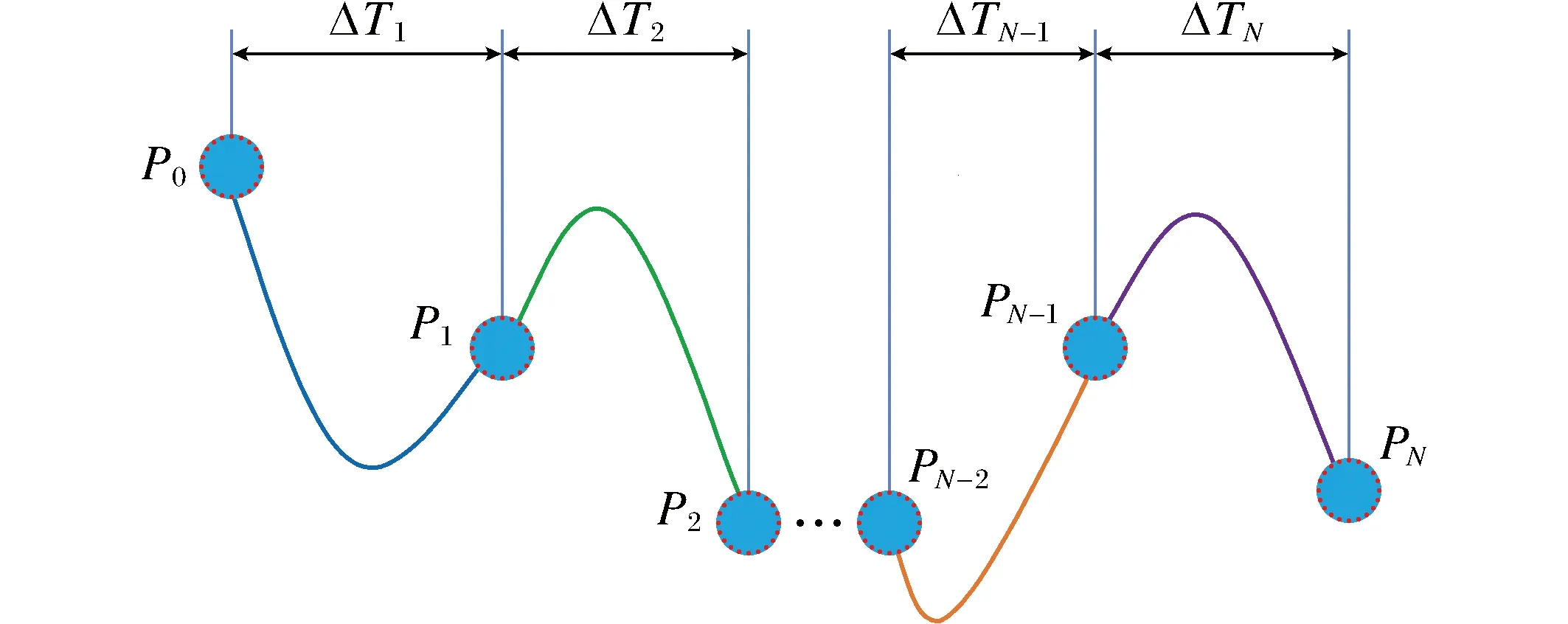
图5 约束条件建立示意图Fig.5 Schematic diagram of constraint establishment

图5中P0,P1,…,PN点为机器人将要经过的点序列,每2点间经时间均匀化分别形成轨迹,式(9)是导数约束模型.

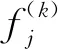
(9)

第j条轨迹在第Tj时刻的k阶导数需要满足起点终点边界条件以及中间点位置约束.这里k取1、2、3、4,表示轨迹中最后一个位姿点与下一段轨迹中第1个位姿点的位置、速度、加速度及加速度的变化率分别对应相等.将式(9)按矩阵展开,得到式(10),

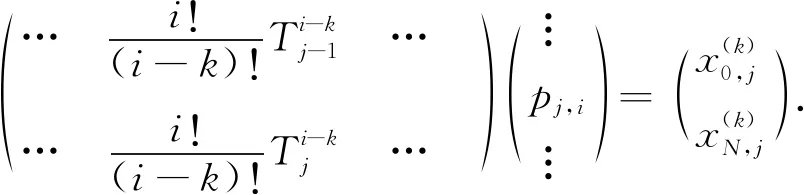
(10)

简化模型为式(11),

Ajpj=dj.

(11)

式中Aj是轨迹在此时刻的已知量,pj为轨迹系数向量,dj为此时刻机器人的边界条件或者中间点位置值.

为保证机器人运动过程柔顺,建立连续性约束,见式(12).

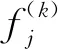
(12)

式(12)表示j轨迹在Tj时刻的k阶导数与其相连接的下一段轨迹在Tj时刻的k阶导数相等.这里k取1、2、3、4,表示轨迹中最后一个位姿点与下一段轨迹中第1个位姿点的位置、速度、加速度及加速度的变化率分别对应相等

将式(12)以矩阵形式展开得式(13):

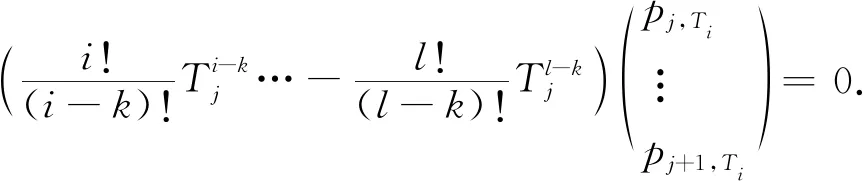
(13)

将轨迹系数整理成列向量,如式(14):

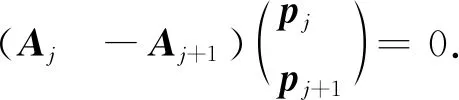
(14)

结合式(11)和式(14)整理成等式约束,将优化模型转化为二次规划问题,目标函数为式(15),约束条件为式(16).

在MATLAB中有求解标准二次规划问题的工具箱,使用QP求解器并调用quadprog函数求得相应数值解即可.

3 实验与分析

3.1 实验设计

本文设置了2组测试实验.第1组为仿真实验,主要用于说明算法的优化效果,算法测试软件平台为MATLAB 2016b.第2组实验是真机测试实验,用于验证算法的可行性,实验平台为自主设计实现的基于ROS kinetic的移动机器人,图6是移动机器人实物图.

图6 移动机器人实物Fig.6 Robot used in the experiment

3.2 仿真结果与分析

对时间均匀化处理后的A*路径结果做最小化snap优化,同时针对起点、终点的空间状态量以及相邻段间位置、速度、加速度连续建立等式约束,实验结果如图7所示(无量纲)(见封3).

图中红色◆为A*搜索得到机器人路径代价最优情况下所需经过的节点,黑色折线表示A*算法给出的机器人最优运行路径,红色平滑曲线为本文算法优化轨迹.

经过仿真实验可以看出,轨迹在平滑度上有了明显改善.相邻中间路径点实现了满足真实机器人速度、加速度连续条件的平滑软连接.

3.3 真机测试实验

在真实环境中完成2D栅格地图建立,将本算法部署在机器人上进行测试,图8(a)是算法在室内环境中生成的3组轨迹效果图,图8(b)是机器人在室外环境中巡检测试效果.验证了机器人具有安全运行的能力,提升了轨迹的平滑性和鲁棒性.选用轨迹长度、轨迹生成时间作为评价标准,同时也提出机器人转弯效率评价标准.

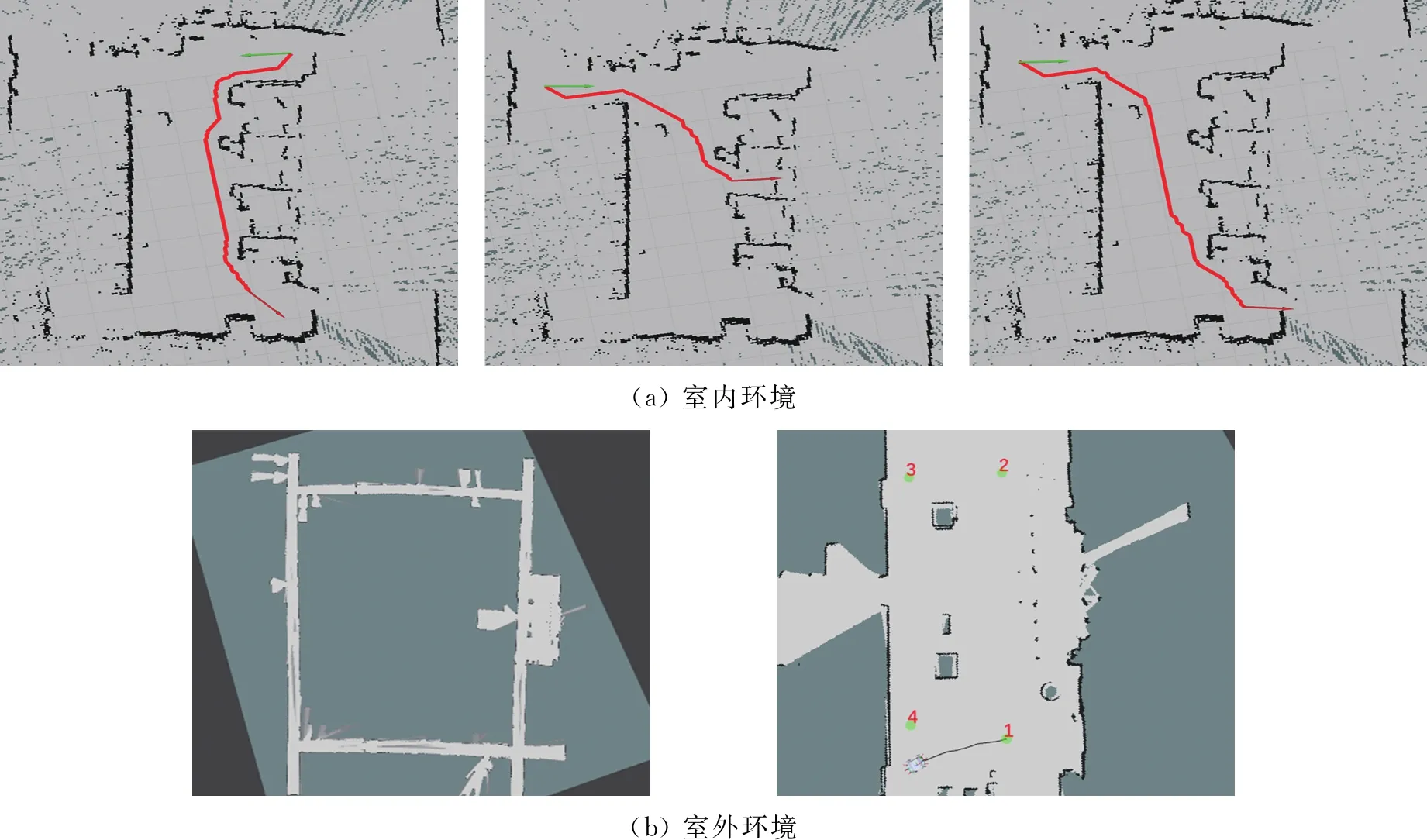
图8 真机测试实验效果Fig.8 Effect diagram of real machine test experiment

转弯效率(η)以真实机器人通过所有弯道的时间间隔的期望作为评价标准.

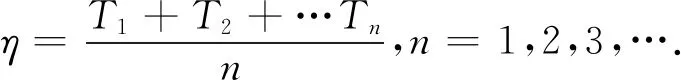
(17)

式中:T1,T2,Tn表示机器人通过弯道的时间间隔;n表示转弯的个数.任意定义4个巡逻点开展真机测试实验.性能对比如表1所示.与传统A*算法相比,本文算法缩减了7.24%的轨迹长度,机器人转弯效率提升了26.88%,证明本文算法在实际应用中具有良好的可行性.

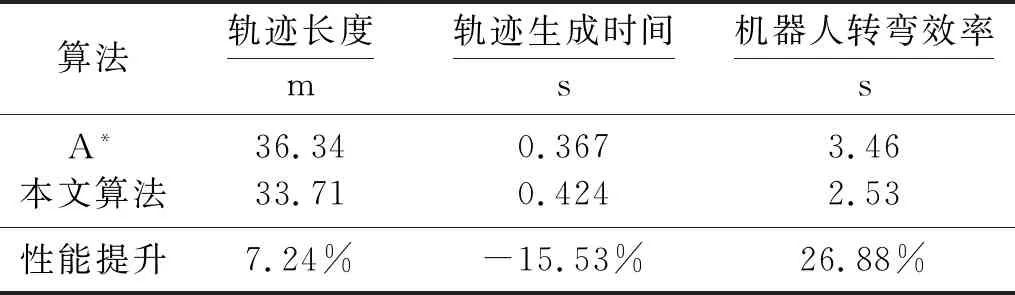
表1 算法性能对比Table 1 Comparison of algorithm performances

4 结 论

针对A*算法存在转角大、折线多且应用于移动机器人时轨迹平滑性差的问题,提出一种基于最小化snap改进A*的轨迹优化算法.将离散路径点用分段多项式曲线化描述,且将机器人的各项动力学性能指标引入轨迹生成约束,使所得路径相对较短,更适合真实机器人的顺滑控制与执行.通过仿真和真机测试,算法在轨迹长度方面缩减了7.24%,机器人转弯效率提升了26.88%.