LIPS-200离子推力器非预期电击穿特性的初步分析

2021-09-03张雪儿张天平李得天孟伟

中国空间科学技术 2021年4期

张雪儿，张天平，李得天,*，孟伟

1. 兰州空间技术物理研究所，兰州 730000 2. 真空技术与物理重点实验室，兰州 730000 3. 甘肃省空间电推进技术重点实验室，兰州 730000

1 引言

离子推力器在具有比冲高、性能调节便利、适用范围广、技术成熟度好等明显优势的同时[1-2]，也存在非预期电击穿问题[3-5]。已有研究表明离子推力器的非预期电击穿现象具有普遍性、复杂性和挑战性[3-9]：在工程应用中通过采取针对性控制与防护措施，可以把非预期打火频次及影响降低到航天任务可接受的程度，但仍然难以完全消除，并且随着更高比冲、更大推力密度离子推力器的开发研制，离子推力器非预期击穿问题正将变得更加棘手[2,8]。

中国离子电推进经过40多年的发展，已经步入航天工程应用并快速扩展的阶段[1,10]，正确认识离子推力器非预期电击穿问题、深入理解相关机理与规律、采取稳妥的控制与防护工程措施变得非常重要和迫切。本文针对中国相对成熟的LIPS-200离子推力器产品，基于比较完整的地面寿命试验非预期击穿基础数据，采用基础数据对比分析、选定模型统计分析、因果关联探索与推断分析等方法，进行了非预期击穿的平均特性、时变特性和天地差异特性等研究，结合推力器实际工况和环境，对击穿特性与主要诱发因素之间的关联性进行了讨论。

2 LIPS-200离子推力器非预期电击穿的基础数据

2.1 选取基础数据的基本考虑

兰州空间技术物理研究所最早从1974年开始做离子电推进技术研究，截至目前开发研制的LIPS系列离子电推进产品如表1所列。

表1 LIPS系列离子推力器基本情况

在选择离子推力器非预期电击穿基础数据时，主要有如下考虑：

1)离子推力器成熟度高，技术成熟度至少达到NASA的TRL9级，产品成熟度最低为鉴定(定型)产品，最好是飞行产品，成熟度高的产品数据具有代表性和工程价值。

2)数据能够覆盖推力器经历长期工作时间，因为击穿特性具有明显的随累计工作时间变化的分布特征[7]。

3)推力器产品数据既有空间飞行应用，又有地面长寿命试验，以便能够进行天地不同因素影响击穿特性的差异性对比，分析结果对中国航天工程应用离子推力器更具价值和意义。地面和空间为同一款产品会更好，具有直接对比的更好基础。

4)数据具有相对完整的基本研究要素，包括时间分布的击穿频次特性、明确对应的推力器工况及环境条件、诱发击穿发生的主要因素等。

基于以上考虑，选择了工作模式单一，试验循环完全一致的LIPS-200[11]离子推力器的击穿情况作为分析的基础数据来源，如表2所列。由于LIPS-200在空间应用中没有采取非预期击穿次数在轨统计技术，只有地面数据。

表2 击穿特性研究对象及数据来源

本文仅分析工作模式单一、试验循环完全一致的LIPS-200离子推力器，而情况复杂得多的LIPS-300离子推力器将在另文分析。

2.2 LIPS-200离子推力器的基础数据

LIPS-200推力器已经完成了SJ-9A的首次空间飞行试验验证，正在CS-16(SJ-13)卫星上进行通信卫星南北位保任务的首次正式应用。LIPS-200离子推力器在地面完成了12 000 h寿命试验[12-14]，图1所示为寿命试验中以每500 h为一个小节的击穿次数统计情况。

图1 LIPS-200试验各小节对应击穿次数Fig.1 Breakdowns in each test segment for LIPS-200

3 非预期电击穿的时间分布特性分析

3.1 非预期电击穿的平均特性分析

LIPS-200推力器地面试验采用单一工作模式，整个过程为2 h工作和0.5 h关机的循环。从图1数据可见，各小节(500 h)击穿次数最多23次、最少0次、平均9.5次。12 000 h试验中总击穿次数为229，相应击穿频次为最大46次/每千小时、最小0次、平均19次，对应击穿周期(间隔时间)约为最短22 h、最长500 h、平均52 h。

表3汇总了LIPS-200推力器平均击穿特性与国外典型产品的平均击穿数据，其中美国NSTAR和NEXT的地面试验数据来自John的会议报告[5]。

表3 LIPS-200与国外产品地面试验中击穿特性的对比

综合比较可见，LIPS-200离子推力器地面试验中的平均击穿频次相对NSTAR和NEXT的地面试验为最低，主要原因是LIPS-200的栅极间电场强度小[7]。

3.2 非预期电击穿的时变特性分析

LIPS-200推力器寿命试验中击穿次数随试验小节和工作时间的累积情况分别如图2和图3所示，由图1数据可见，LIPS-200推力器的全寿命周期击穿特性大致可分为三个不同频次阶段：0-7 500 h(对应1-15小节)的前期阶段，击穿频次较高，平均为每千小时24.8次；7 501-10 000 h(对应16-20小节)的中间阶段，击穿频次较低，平均为每千小时4.8次；10 001-12 000 h(对应21-24小节)的后期阶段，击穿频次又有升高，平均为每千小时15.5次。结合具体试验情况分析确认的主要原因为：1-15小节的前期阶段，每小节试验后推力器要暴露一次大气，由此导致推力器电极表面的吸气出气过程和溅射沉积物的局部开裂，使得击穿频次相对较高；中间和后期阶段，每小节试验后推力器进入闸舱不再暴露大气，消除了吸气出气因素并降低了沉积物局部开裂因素影响，使得中间阶段的击穿频次达到最低；后期阶段击穿频次又有所上升的主要原因是随溅射沉积物厚度增加导致的局部开裂又有所增强所致。

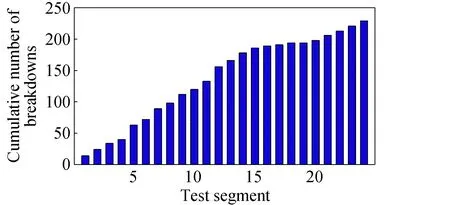
图2 击穿次数随试验小节累积情况Fig.2 Cumulative number of breakdowns with test segment

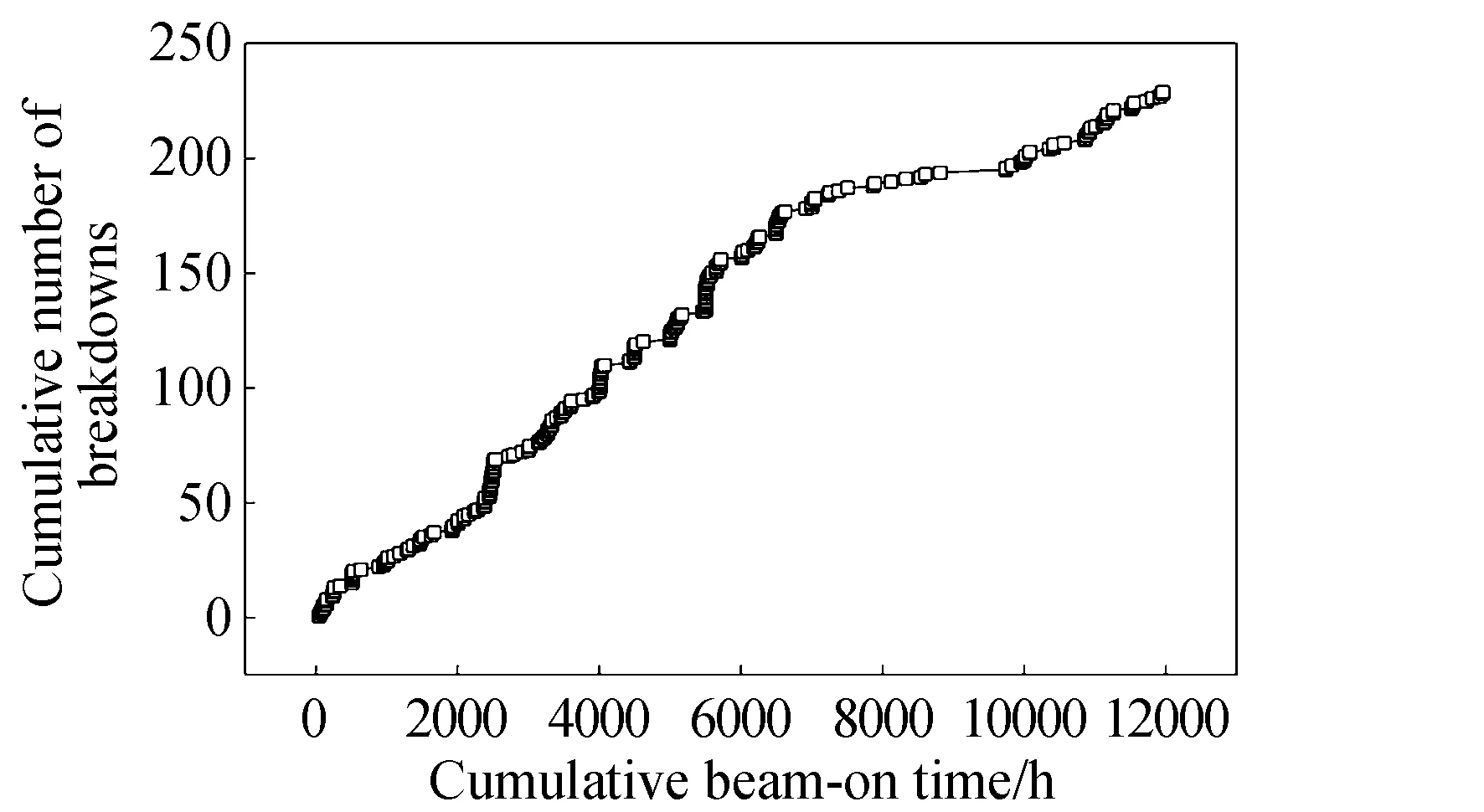
图3 击穿次数随工作时间累积情况Fig.3 Cumulative number of breakdowns with test time

结合图2和图3中的击穿次数累积趋势来看，在每一试验小节的开始时段击穿频次均较高(对应图3中曲线上升较快)，为此将每个试验小节划分为25个循环(cycle)，每个循环包括连续的10个2 h工作、0.5 h关机的过程。对各循环内的击穿次数进行了统计，结果如图4所示，其中每个循环的击穿次数为各试验小节对应时段内次数的合计。可见在25个循环中，发生在第一个循环内的击穿次数最多，高达66次，占总次数的29%；第二个循环的击穿次数次之，为17次；其他23个循环的击穿次数在3-11之间随机分布。该结果说明，在各试验小节开始时的前两个循环内发生的击穿次数占总次数的36%以上，进一步验证了每个试验小节前的暴露大气、沉积物局部开裂等因素是造成高击穿频次的根本原因，该影响因素随着击穿产生的蒸发效应逐渐消除后，击穿频次降低并趋于随机稳定。

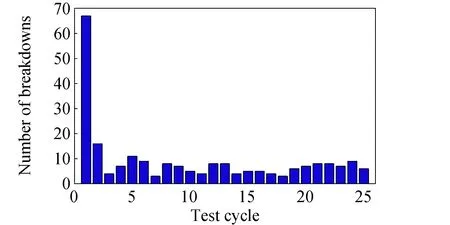
图4 各循环内击穿次数的分布Fig.4 Number of breakdowns in eachcycle

类似的时变特性分析还可以沉底到2 h工作、0.5 h关机的小循环(subcycle)中，主要结果如图5所示，横坐标为工作时间的百分位，纵坐标为击穿次数；其中每组击穿次数都是所有小循环中相应时段次数的合计。由此可见，对于这些小循环，其工作时间前10%内的击穿频次比其他时段高出近一倍，该结果同样可以用污染物影响机制解释：小循环启动过程中，推力器热状态显著变化且束流尚未完好聚焦，由此引起沉积物局部开裂以及束流离子轰击，击穿概率明显增加。

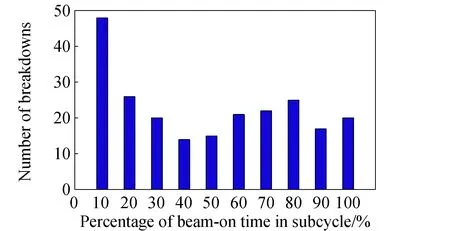
图5 小循环内击穿次数随时间的分布Fig.5 Number of breakdowns with percentage of time insubcycles

4 击穿特性的威布尔统计分析

4.1 威布尔统计分析方法

威布尔分布模型最早用于小子样材料断裂强度统计，现在多用于产品寿命预测分析，威布尔分布的横坐标为寿命、开关周期、工作时间、任务时间等，纵坐标为事件发生概率。由于其具有图像解释简单直观、对试验子样数据要求不高、且能够提供失效机理线索等突出优点，通过参数调整适用于大量类别产品，并应用于地震、艾滋病等离散现象的分析。离子推力器非预期击穿现象具有非常强烈的随机离散特性，应用威布尔模型进行分析是一种合理可行的选择[9,15]。

针对离子推力器非预期电击穿事件，将击穿间隔时间(击穿周期)作为变量，则对应周期内发生击穿的概率就是击穿事件的累积分布函数(CDF)，其威布尔双参数表达以及概率密度函数分别为

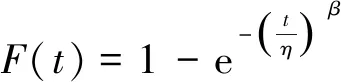
(1)

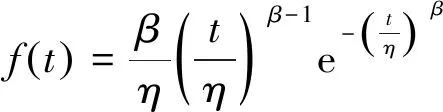
(2)

式中：t为击穿周期；F(t)为击穿事件的累积分布函数；f(t)为概率密度函数；η为时间标度因子，通常表征击穿周期数据的特征水平；β为形状因子，通常表征击穿周期的发展变化趋势,β小于1表明击穿事件处于增长期或将引起后续更多击穿，β大于1表明击穿周期随时间增加，也就是击穿频次呈下降状态；β等于1则表明击穿频次稳定。

对击穿周期特性进行威布尔模型分析，期望达到的目的主要包括：

1)基于推力器基础数据，采用拟合或近似方法，获得推力器击穿周期的概率密度函数和累积分布函数；

2)应用击穿周期概率密度函数，进行基本特征量的估算或预测，具体包括平均值(期望值)、均方根值、p分点值等；

3)通过分类分析及解耦方法，给出不同主要影响因素所对应的分布函数及特征统计值，主要影响因素包括出气、污染物、电场强度、束流密度等；

4)回归分析，结合前述分析结果及关系规律，预测一个特定航天任务中离子推力器的非预期击穿发展演化过程，确定重点防护应对措施。

4.2 LIPS-200非预期电击穿周期的威布尔分析

首先处理基础数据，完成击穿次数与击穿周期之间的转换。由于击穿数据较多且周期分布差异很大，为此按击穿周期量级共划分为五个档，表4列出了综合分档后的结果。

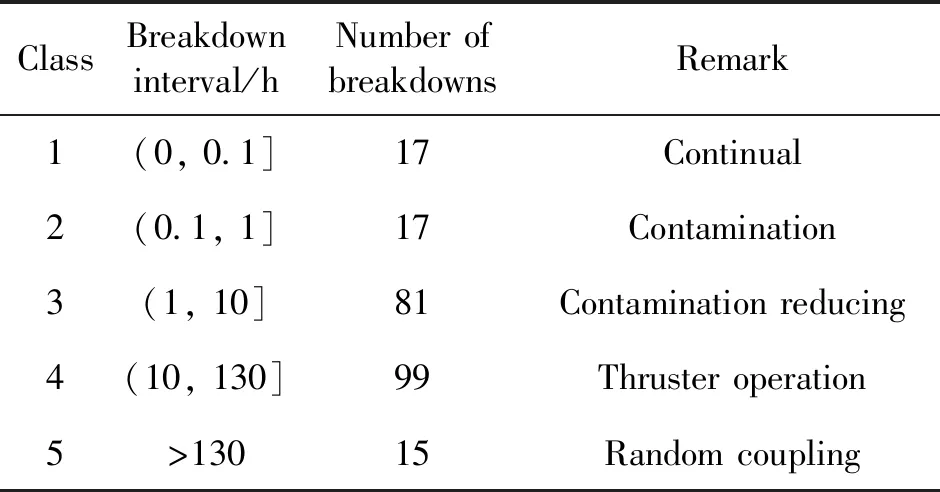
表4 LIPS-200推力器击穿周期的分档结果

第1档为最短击穿周期类别，对应于发生近似连续击穿的情况，其主要机制是导致击穿发生的主要因素不能通过一次击穿而消除，如多余物尖端(微凸)、持续出气等情况；第2档为短周期类别，主要对应于推力器受到明显污染的情况，如推力器暴露大气、推力器热状态变化导致沉积物局部开裂等；第3档为中等周期类别，对应于从推力器受到明显污染到污染源基本消除的过渡阶段，因此该档周期常见于地面试验，明显区别于飞行应用；第4档为长周期类别，对应于推力器本征因素影响下的随机击穿特性，如推力器内部溅射沉积物、真空舱漂移溅射物等；第5档为超长周期类别，对应于推力器基本工况条件下其他随机因素的耦合影响。

实际上仅就地面试验而言，各档之间很难严格划分清楚，相互之间都有耦合过渡，特别是推力器内部溅射沉积物和推力器外部真空舱溅射沉积物的影响总是耦合在全试验过程中。本研究采用的五档划分是具有一定合理性的尝试，下面分别对各档击穿周期进行威布尔分析。

(1)最短击穿周期的统计分析

17次近似连续击穿的次数与周期统计数据如图6所示，累积概率分布曲线及其威布尔分布拟合如图7所示，得到最短周期击穿事件的累积分布函数为：

图6 第1档击穿次数随周期的分布情况Fig.6 Number of breakdowns with interval in the 1st class

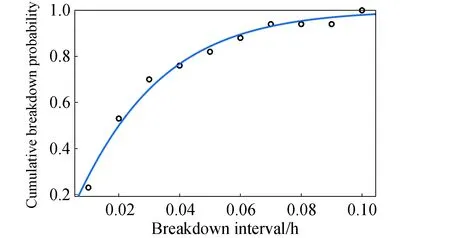
图7 第1档累积击穿概率的周期分布及其威布尔拟合Fig.7 CDF for breakdowns in the 1st class and its Weibull distribution fitting

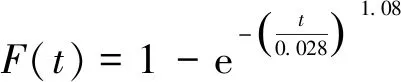
(3)

即威布尔分布的时间标度因子为0.028 h，基本对应于击穿发生后的试验系统重启时间(控制在100 s量级)。分布的形状因子为1.08，即击穿频次基本稳定且呈缓慢降低趋势，与实际情况也基本相符。

(2)短击穿周期的统计分析

17次短周期击穿的次数与周期统计数据如图8所示，累积概率分布曲线及其威布尔分布拟合如图9所示，由此得到的时间标度因子为0.38 h，基本对应于推力器存在污染的情况下每小时几次的典型击穿频次量级。分布形状因子为1.24，对应衰减趋势进一步加快，也符合污染影响会逐渐减小的预期。

图8 第2档击穿次数随周期的分布情况Fig.8 Number of breakdowns with interval in the 2nd class

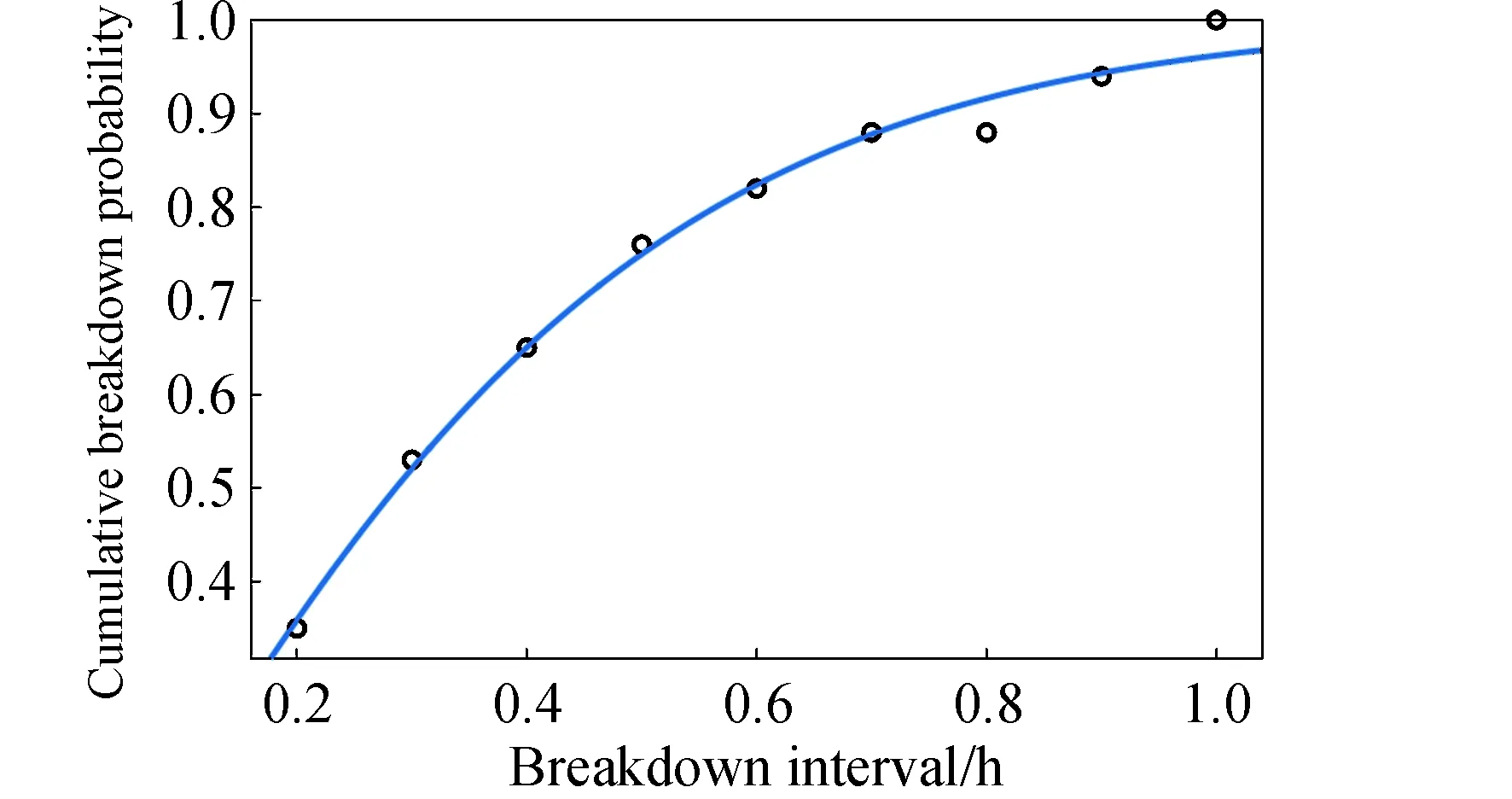
图9 第2档累积击穿概率的周期分布及其威布尔拟合Fig.9 CDF for breakdowns in the 2nd class and its Weibull distribution fitting

(3)中等击穿周期的统计分析

81次中等周期击穿的次数与周期统计数据如图10所示，累积概率分布曲线及其威布尔分布拟合如图11所示，由此得到相应击穿周期累积分布函数的时间标度因子为5.8 h，对应于暴露大气后污染影响基本消除的时间量级。分布形状因子为1.65，表明污染影响消除进一步加快、击穿频次的衰减趋势更明显，符合实际污染清除过程的特点。

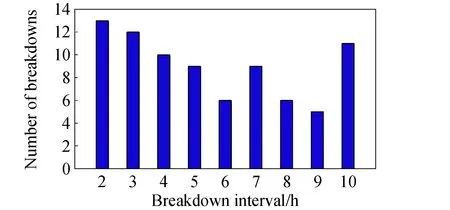
图10 第3档击穿次数随周期的分布情况Fig.10 Number of breakdowns with interval in the 3rd class

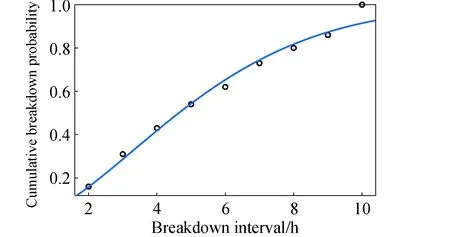
图11 第3档累积击穿概率的周期分布及其威布尔拟合Fig.11 CDF for breakdowns in the 3rd class and its Weibull distribution fitting

(4)长击穿周期的统计分析

99次长周期击穿的次数与周期统计数据如图12所示，累积概率分布曲线及其威布尔分布拟合如图13所示，由此得到累积分布函数的时间标度因子为50.1 h，基本对应于整个试验的平均击穿周期(52.4 h)。分布形状因子为1.23，对应于栅极溅射沉积率随累计工作时间逐渐减小时，击穿频次呈响应衰减趋势。

图12 第4档击穿次数随周期的分布情况Fig.12 Number of breakdowns with interval in the 4th class

图13 第4档累积击穿概率的周期分布及其威布尔拟合Fig.13 CDF for breakdowns in the 4th class and its Weibull distribution fitting

(5)超长击穿周期的统计分析

15次超长周期击穿的次数与周期统计数据如图14所示，累积概率分布曲线及其威布尔分布拟合如图15所示，由此得到的时间标度因子为256.8 h，基本代表了推力器超长击穿周期的典型值。分布形状因子为3.1，对应的击穿频次衰减趋势非常大，可能由于导致击穿的随机个体因素的耦合效应随工作时间累积逐渐退化，其详细机制有待进一步探究。

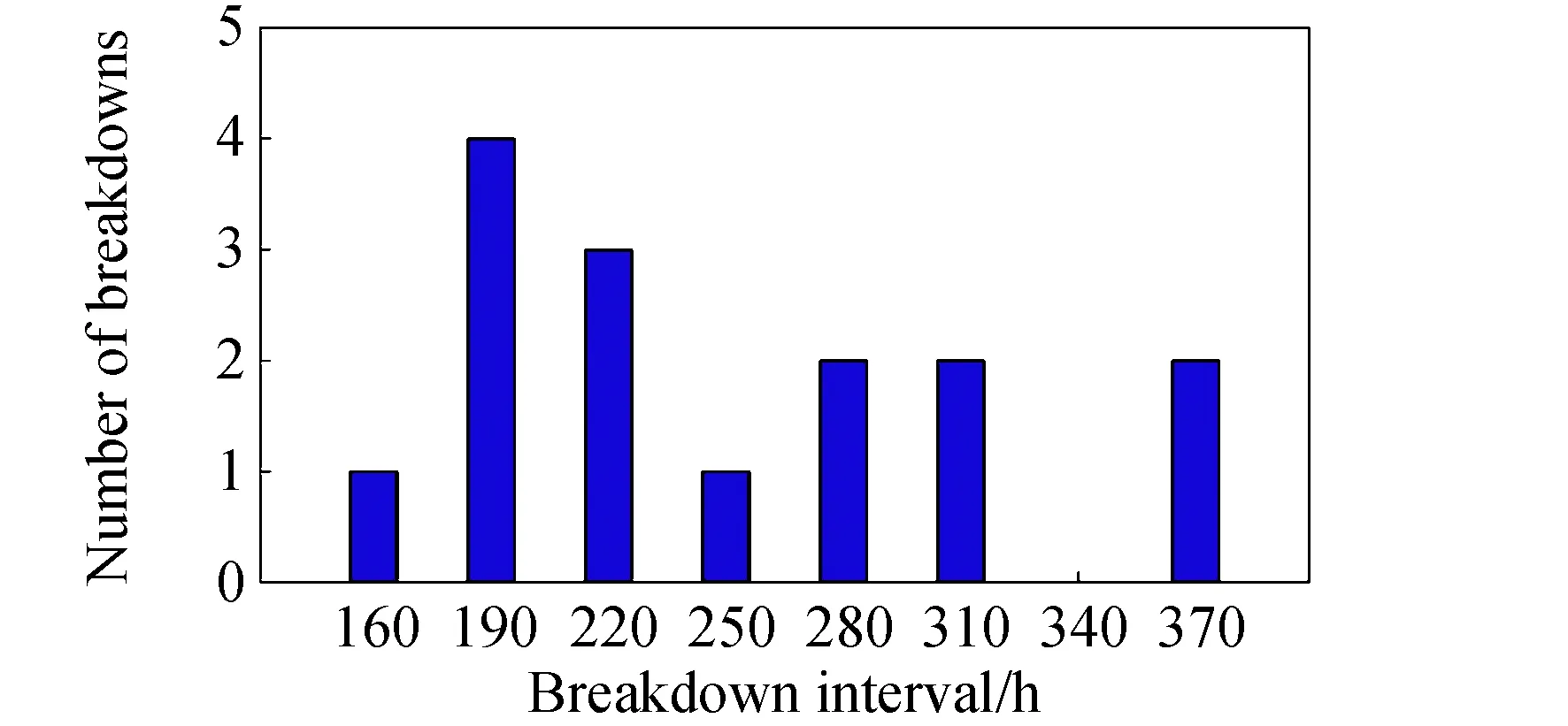
图14 第5档击穿次数随周期的分布情况Fig.14 Number of breakdowns with interval in the 5th class

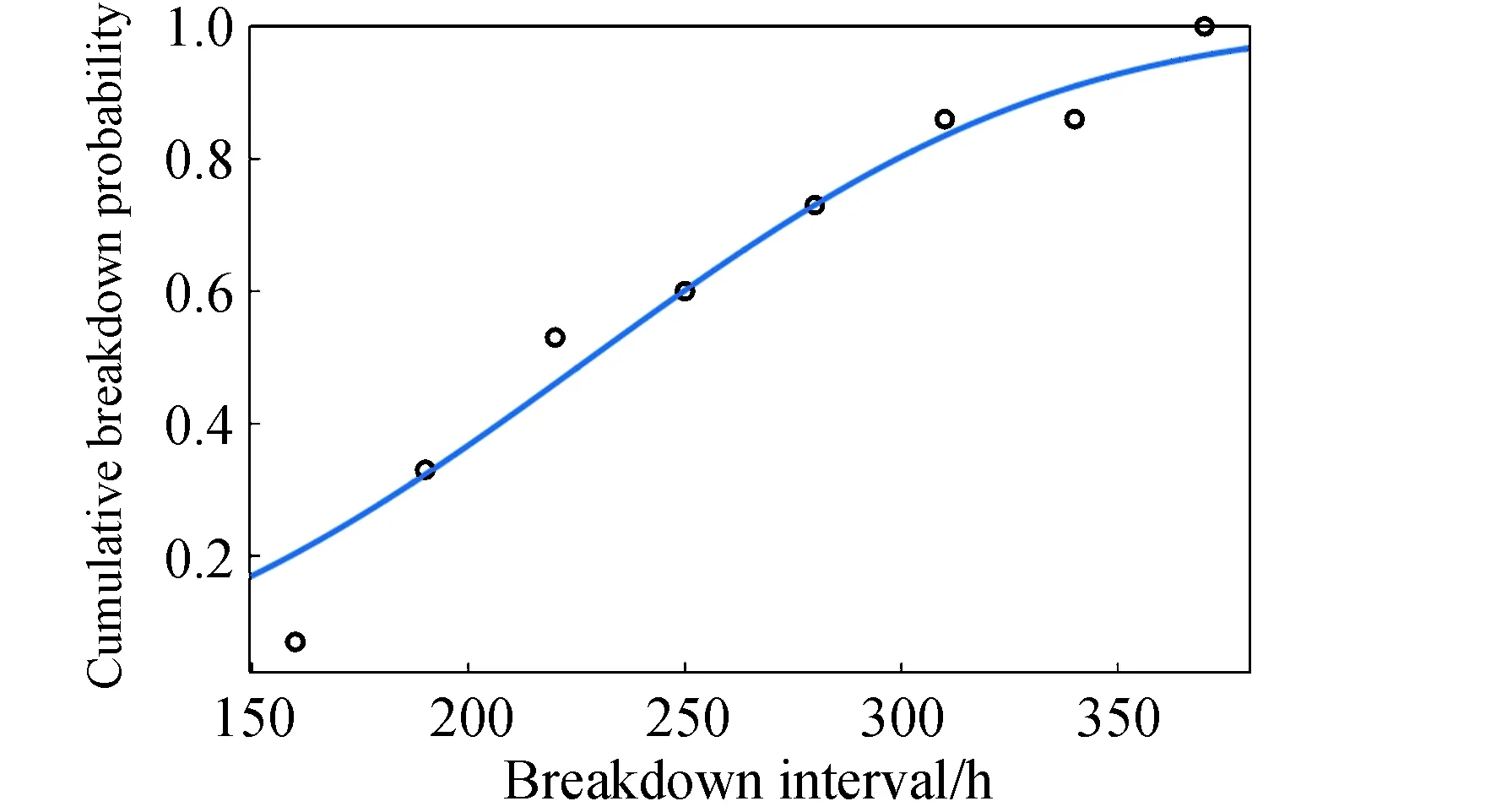
图15 第5档累积击穿概率的周期分布及其威布尔拟合Fig.15 CDF for breakdowns in the 5th class and its Weibull distribution fitting

4.3 威布尔统计分析结果评述

表5给出了LIPS-200分档击穿周期的威布尔统计分析结果，从各档威布尔统计参数与各档非预期击穿主要影响因素之间的对应关系看，其特征时间(时间标度因子)是基本合理的。形状因子都大于1意味着击穿频次呈减小(周期增大)趋势，并且各档形状因子间的相对大小也具有合理的过程机制解释：第1档形状因子最小且接近于1，对应于引起击穿的因素未能消除而出现的近似连续击穿，击穿频次相对稳定；第2档形状因子为1.24，对应于污染类击穿因素影响程度的逐渐弱化过程，相应的击穿频次出现逐渐降低的趋势；第3档形状因子进一步增大到1.65，因为污染因素在击穿老炼过程中步入加速消除的阶段，击穿频次降低趋势变快；第4档形状因子为1.23，与第2档基本相当，但这里对应于溅射沉积物的影响，其大小与栅极溅射沉积率随累计工作时间逐渐减弱的趋势一致；第5档的形状因子最大，除了前述的耦合因素影响外，其他次要单因素作用的逐渐弱化也是潜在机制之一。

表5 LIPS-200推力器击穿周期的威布尔分析结果

由于受到不同诱发因素的影响，击穿事件在不同工作时段的发生概率差异很大，通过对击穿周期的初步分档获得了较为合理的Weibull拟合参数，也揭示了主要因素影响下击穿事件的分布特性。对于各因素间耦合作用以及其他次要因素的影响，需要结合数据检验和相关性分析方法(如卡方检验、回归分析等)对数据进行更为精细的处理，以获得更具统计学意义的结果。