时间与燃料约束的参数自主寻优变轨滑模控制

张晗，康国华，*，张琪，魏建宇，戴涧峰

1. 南京航空航天大学 航天学院，南京 211106 2. 航天东方红卫星有限公司，北京 100094

1 引言

在航天器轨道机动中通常需要根据期望(标称)轨迹对轨道进行控制，矫正运动中的位置与速度误差。为适应复杂空间环境的影响，要求运动控制策略必须满足强鲁棒性、高精度及稳定性等性能属性[1-2]以及安全避障、有限时间收敛、燃料消耗等特定约束条件。

针对空间相对动力学的控制问题，文献[3]基于状态转移矩阵研究了空间多脉冲悬停的多脉冲控制方法。文献[4]使用高斯伪谱法生成了航天器交会逼近问题的优化解决方案，并使用闭环控制对轨迹进行跟踪优化。文献[5]提出一种以最小时间算法执行航天器大角度机动的改进滑模控制方法，并与先前开发的控制方案本征四元数调节器进行对比，验证了该算法的优越性。为保障追踪航天器的安全，文献[6]针对航天器近距离逼近问题，在建立的相对运动和避碰模型的基础上，设计了考虑外界扰动上界已知和未知两种情况下的有限时间收敛避碰控制器，并通过Lyapunov理论和避碰势函数证明控制器系统能在有限时间收敛。上述方法成功地将多种约束条件引入航天器相对动力学模型中，为本文提出的滑模控制约束条件的引入提供了基础。

随着航天器任务变轨需求的增加和轨控能力增强，目前很多成熟控制方法开始应用于航天器相对变轨任务中。其中，滑模控制(sliding mode control, SMC)因其良好的鲁棒性以及扰动抑制能力[7]，被广泛使用。文献[8]提出一种鲁计模糊神经网络(FNN)自适应调节滑模控制器，能够在航天器质量分布改变时仍然保持控制器的有效性和稳定性。文献[9]就椭圆轨道上的航天器近距离无碰撞交会相对运动控制进行了研究，提出一种结合最优滑模控制(OSMC)和人工势函数(APF)的防撞自主混合控制算法，实现空间交会的无碰撞接近控制。上述算法基于有限时间、最优控制以及防碰撞等约束条件，与滑模控制理论相结合进行了研究，并成功应用到航天器变轨控制任务中，为本文研究多约束的变轨滑模控制奠定了工程实现基础。

然而，在实际的航天器轨道相对运动控制任务中，滑模控制器控制参数取值直接影响了控制的效果和精度[10]，以及燃料消耗的情况。基于此，本文在指数趋近的滑模控制器基础上，提出一种综合考虑时间、燃耗以及误差的参数自主寻优规则。首先，深入分析了各项控制参数在量级取值上的约束条件，融入避碰时间约束制定了控制参数量级寻优规则；其次，采用惯性权值优化的粒子群算法设计了燃料最优、误差有界的多输出适应度函数，并综合考虑误差和燃料约束，确定了系数寻优规则；最后，输出最优量级/系数组合的控制参数，实现有限时间内的状态收敛，使消耗的燃料尽可能最少。

2 问题描述

根据航天任务的实际需求，在以目标航天器为原点建立的相对运动坐标系中，通常要求追踪航天器(Sat)在控制指令存在初始误差和受外界扰动的情况下，能够在有限时间内其运动轨迹收敛至轨迹规划器输出的任务标称轨迹(期望轨迹)，如图1所示。

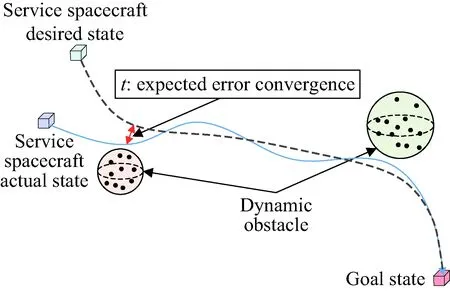
图1 相对运动坐标系中的轨迹修正控制Fig.1 Trajectory correction control in relative motion coordinate system

鉴于当前空间碎片威胁以及目标机动等突发因素，该控制过程要求具有抗扰能力：可以处理紧急避障及时间最短等突发情况。这类相似问题，通常采用滑模控制[11]处理，但该算法：

1)依据经验人工调节控制参数，自主性弱；

2)通常以误差收敛精度作为唯一标准，未考虑时间、燃料约束；

3)容易因参数设置不合理引起控制抖振[12]。

鉴于轨迹的安全性与燃料的重要性，针对上述问题，需设计一种能够需要满足如下规则的控制器：

1)可自主完成滑模控制器参数设置；

2)具有实时避障能力，轨迹躲避障碍物收敛至标称轨迹允许误差范围内；

3)满足燃料、时间最优等参数设置要求，且避免抖振。

根据上述目标，选择合适的指数趋近律对滑模偏差控制器进行建模。

3 滑模偏差控制器建模

滑模控制作为一类特殊的非线性控制，主要包含两部分：设计合适的滑模面；选择合适的趋近律使系统状态向滑模面运动。当系统状态到达滑模面后，在滑模面的约束下系统状态误差将实现收敛。构建相对变轨控制中滑模偏差控制器：

(1)

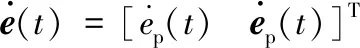
s=λe(t)=Cep(t)+Iev(t)

(2)

式中：k=diag[kx,ky,kz]与ε=diag[εx,εy,εz]是待寻优的三维参数。构成的滑模偏差控制器：

(λB)-1[-λAe(t)-ks-εsgn(s)]

(3)

为验证控制器的有效性，需要证明其稳定性。首先，根据上述滑模偏差控制器构建Lyapunov函数如下：

然后，对上式进行求导得：

-ks2-ε|s|

(4)

4 控制模型参数自动寻优策略

在式(1)滑模偏差控制器模型基础上引入滑模控制参数自主寻优器，使其具有参数自主设置的能力，构建的航天器相对运动轨迹修正控制器如图2所示。

图2 航天器相对运动轨迹修正控制器Fig.2 Spacecraft relative motion trajectory correction controller

图2中的PSO为粒子群算法(particle swarm optimization)。通过分析发现，滑模初始化的控制参数存在无法寻优情况，即在粒子迭代寻优之前初始化参数本身无最优空间或寻优耗时极长；通过对各种初始化参数对比分析发现，若已知各控制参数的具体量级，在此基础上使用粒子算法寻找各参数对应量级下的最优系数，可使寻优的效果更加快速，精确。因此，这里设置的参数量级分析模块，可以通过考虑Lyapunov条件、收敛时间以及外界干扰的约束关系，确定各参数对应的具体最优量级。然后将各参数量级作为后续系数寻优模块的输入条件，从而更加快速、准确地找到最优控制参数。不失一般性，对图2算法对应的场景作如下假设：

1)航天器受到的干扰力量级已知，范围有限；

2)轨迹规划器已经输出了符合能量最优的标称状态与标称控制；

3)目标航天器未施加主动控制，追踪航天器具有机动能力(各个方向均安装推力器，可提供任意矢量方向的推力，施加推力前不需要建立点火姿态)；

4)轨迹规划器所进行的避障判断准确有效，能够为滑模控制参数寻优器提供精确的时间约束，使其在该时刻实际状态收敛后就能实现避障。

基于以上假设，对图2中虚线框出部分进行设计，主要分为量级寻优策略与系数寻优策略两类。

4.1 量级寻优策略

(1)参数k与ε的量级寻优策略

通过分析，若想让滑模面在有限时间内达到稳定点，需修改Lyapunov条件为：

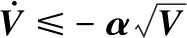
(5)

式中：α为引入的三维中间变量。对改进后的条件进行分离变量和积分：

(6)

式中：tcv为滑模面收敛至0时间。对式(6)左边积分：

整理式(6)得到α与tcv之间的关系为：

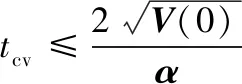
(7)

联立式(4)(5)得到控制器参数k与ε约束关系为：

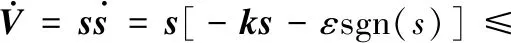
也就是说，只有满足上式才能使滑模面在有限时间内收敛，故将其作为量级寻优策略的基础。

综合考虑状态误差、滑模面以及控制的有限时间收敛，通过多次调参测试(见表1)，基于如下假设构建参数k与ε的量级寻优模型：针对参数k，当其与参数α的量级差小于0时，状态误差不收敛，控制输出抖振；量级差大于或等于0时，状态误差收敛，控制输出正常；量级差过大时(大于标准量级差)，控制器几乎失效。于是确定参数k的量级Nk=[Nkx,Nky,Nkz]与参数α的量级Nα=[Nαx,Nαy,Nαz]之间的偏差关系为Dm=Nki-Nαi≥0,i=x,y,z，且经过测试，默认Nki越大，燃料消耗越多。针对参数ε，当其与外界干扰(L)量级差大于0时，控制输出抖振；量级差小于或等于0时，状态误差收敛，控制输出正常。于是确定参数ε的量级Nε=[Nεx,Nεy,Nεz]与干扰的量级NL=[NLx,NLy,NLz]关系为Dm=Nεi-NLi≤0,i=x,y,z，同样经过测试，默认Nεi越大，燃料消耗越多。

表1 待寻优参数多次测试规律总结

根据上述假设与多次测试规律总结，提出以下两条规则用以确定参数k与ε的最优量级：

规则1：对于收敛时间tcv确定的滑模偏差控制器，根据式(7)确定参数向量α的量级Nα，取参数k的量级寻优策略为：Nki-Nαi≥ξ1i,i=x,y,z，其中ξ1=[ξ1x,ξ1y,ξ1z]中各个参数取值范围大于或等于0(初始值为0，依次加1)，直到tcv时状态误差收敛至阈值δtcv；tcv→tF时段收敛至δtcv→tF且不出现抖振，输出确定的参数向量k的最优量级为Nk。

规则2：若已知干扰参数的向量L对应的量级NL=[NLx,NLy,NLz]，取参数ε的量级寻优策略为：Nεi-NLi=ξ2i,i=x,y,z，其中ξ2=[ξ2x,ξ2y,ξ2z]中各个参数取值范围在[δε,0] (初始值为0，依次减1)，直到tcv时状态误差收敛至阈值δtcv；tcv→tF时段收敛至δtcv→tF且不出现抖振，输出确定的参数向量ε的最优量级为Nε，如图3所示。

图3 参数k与ε的量级寻优规则Fig.3 Magnitude optimization rule for parameters kand ε

(2)参数λ的量级/系数确定策略

根据式(3)设计的滑模偏差控制器，能够使整个系统的状态s在有限时间内收敛至滑模面上，但系统的状态误差e(t)只能在无穷时刻才能收敛至零。因此，需要对状态误差收敛的程度进行分析。首先，在式(2)的基础上得出下式：

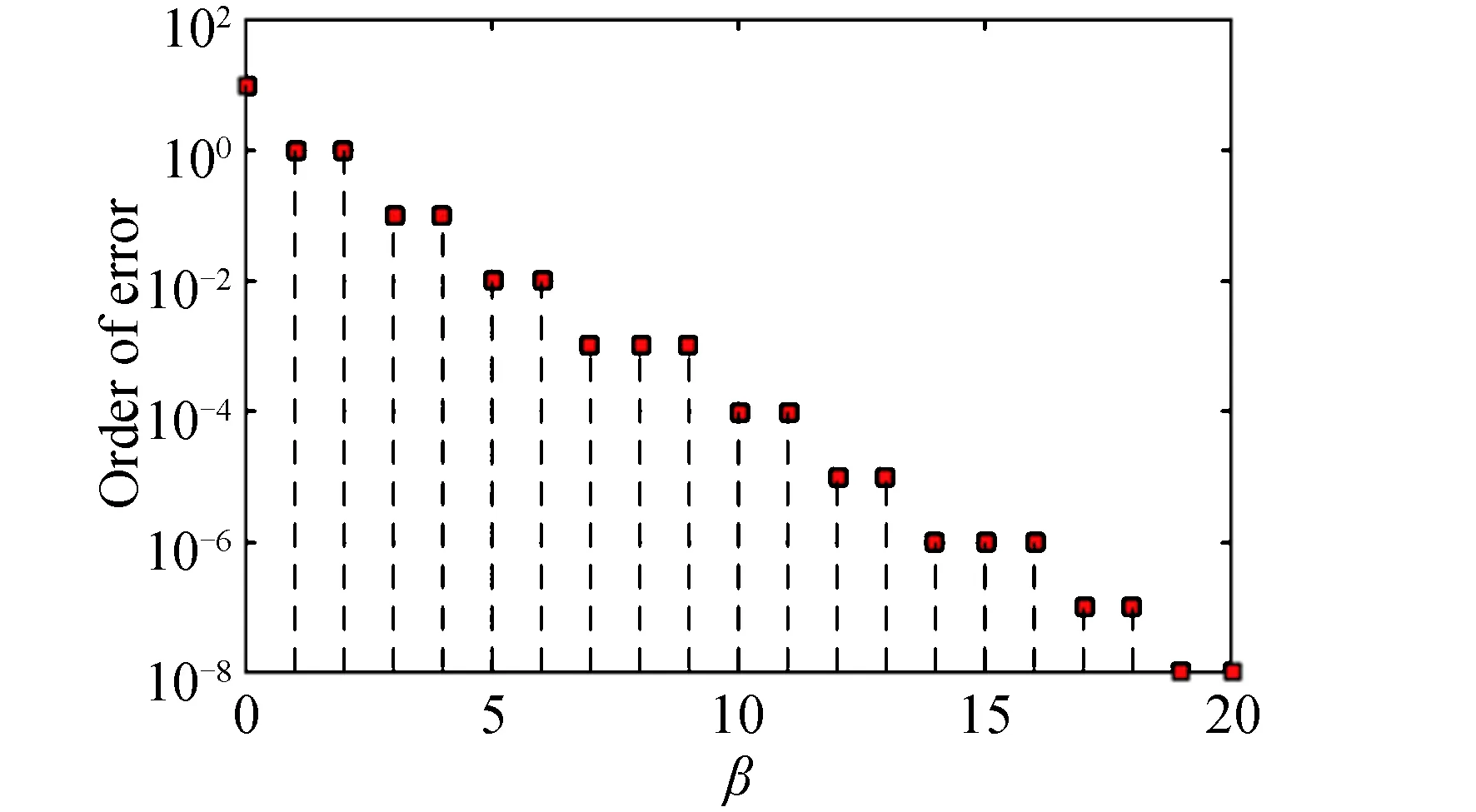
若取状态误差的收敛时间为tcv，且用参数βi=Citcv,i=x,y,z表示状态误差的收敛程度，从而确定误差量级谱的公式如下：

Nβi=[lg |epi(0)e-βi|]

(8)

当参数k与ε一定时，改变参数λ，工质的消耗与收敛的速度成反比。在保障安全的情况下，收敛时间tcv越长，消耗的燃料越少。然后，根据误差精度的要求，确定合适的收敛量级βi，从而确定参数C的值，即确定参数λ。

4.2 系数寻优策略

(1) 惯性权值变化的粒子群算法

传统的粒子群算法在早期的收敛速度过快，极易陷入局部最优[14]。因此，文献[15]引入惯性权值ω用以反映粒子依赖本身运动习惯的程度，将粒子的状态转移方程改写成如下形式：

vi(t+1)=ωvi(t)+c1r1[pi(t)-xi(t)]+

c2r2[g(t)-xi(t)]xi(t+1)=

xi(t)+vi(t+1)

式中：xi(t)=(xi1,xi2,…,xid)表示粒子位置；vi(t)=(vi1,vi2,…,vid)表示粒子方向和速度；i∈[1,N]，N为设置粒子总数;c1和c2表示学习因子，反映粒子对自身历史经验记忆的依赖程度；r1和r2是在[0,1]区间变化的随机加速度权重系数。

惯性权值的设置对算法影响较大，主要规律为：1)当惯性权值ω较大时，算法在全局搜索上表现较强；2)当惯性权值ω较小时，算法在局部搜索上表现力强，收敛性强。已知参数k与ε的量级，以及初始化粒子期间已获得的第1个全局极值对应的最优参数xi(0)。在此基础上，构建惯性权值变化模型：当迭代次数Mj

规则3：对于总迭代次数Mm，给定绝对局部搜索阈值比率为η，于是绝对局部搜索阈值为Mδ=ηMm。当迭代次数Mj

式中：km为收敛系数。当Mj≥Mδ时，令ω=ωmin。

(2)适应度值及其评价规则

1)适应度值。将每个粒子携带的位置信息作为适应度函数的输入，并分别计算该位置信息下的适应度值，将输出的适应度值设置为3个参考量：3轴在时刻tcv的误差绝对值之和eptcv：

eptcv=|epxtcv|+|epytcv|+|epztcv|

式中：epxtcv、epytcv、epztcv为时刻tcv时各轴的误差值；三轴的速度增量Δv为

Δv=

式中：ux、uy、uz分别为在时间段[0,tF]内各轴的偏差控制加速度输出；三轴在时间tcv后的误差平均值eptcv→tF：

eptcv→tF=

2)评价规则。根据3个指标，确定初始化阶段(阶段1，见图4)和更新阶段(阶段2，见图5)的全局极值粒子以及所有粒子的个体极值位置，构建如下评价规则。

图4 阶段1的个体与全局最优更新规则Fig.4 Individual and global optimal update rules of stage 1

图5 阶段2的个体与全局最优更新规则示意Fig.5 Individual and global optimal update rules of stage 2

规则4 (阶段1)：初始化第一个全局极值的系数为g=[9.9,9.9,9.9,9.9,9.9,9.9](即参数k与ε在最优量级下能取的最大值)，然后该粒子的适应度值Fitg[eptcv(g),Δv(g),eptcv→tF(g)]进行计算。当进入循环迭代后，再对每个粒子个体极值pi,i∈[1,N]的适应度值Fiti[eptcv(pi),Δv(pi),eptcv→tF(pi)]进行计算；当同时满足下述条件eptcv(pi)<δtcv，eptcv→tF(pi)<δtcv→tF以及Δv(pi)<Δv(g)时，更新初始全局极值g。如图4所示，虚线框出部分对应规则4的判定条件。

5 仿真校验与分析

5.1 仿真参数设置

利用Matlab搭建算法程序，整个仿真运行环境如表2所示。

表2 仿真环境参数

追踪航天器在存在初始误差与外界干扰条件下，在以目标航天器为坐标原点的相对运动坐标系中，进行相对运动轨迹修正控制，仿真参数如表3所示。

表3 仿真参数设置

在本例中，追踪航天器与目标航天器处于异面状态，初始条件下的追踪航天器在相对坐标系下实际状态误差如表4所示(参考轨道高度500 km，初始相对距离约2.69 km，目标航天器在追踪航天器右前方)。为使整个仿真过程更具一般性，现取3组数据加以验证，并设计最优量级确定策略与最优系数确定策略中的仿真参数如表5所示(扰动施加为-5量级的正弦函数)。

表4 追踪航天器在相对坐标下的实际状态误差

表5 最优量级/系数确定策略仿真参数

5.2 仿真结果与分析

根据表3-5进行仿真环境初始化，分别验证参数自主寻优算法中量级寻优策略与系数寻优策略的有效性。根据式(8)得出的参数β下收敛时间tcv时的误差量级谱如图6所示。

图6 参数β下收敛时间tcv时的误差量级谱Fig.6 Error magnitude spectrum at convergence timetcv under parameter β

由图6分析可知，β的增大使得误差收敛的精度变高，但是，由于βi=Citcv,i=x,y,z(tcv给定)也会直接导致参数C(λ)的增大，从而使燃料消耗增多。于是，β的取值应该在逐渐增大直至满足误差收敛条件的循环中产生。

根据表4中的3组数据(数据编号唯一)，结合参数λ量级/系数确定策略得出λ中参数C的值如表6所示；结合参数k与ε的量级寻优规则得出参数最优量级如表7所示。

表6 β自适应变化时的参数C的取值

表7 量级寻优策略下的各参数量级分布

表6和表7证明了参数λ量级/系数确定策略与参数k与ε量级寻优策略的有效性，以及对控制精度要求变化的适应性。将表6中的值组合形成参数λ，以及表7中参数k与ε的最优量级，作为系数寻优策略的输入，得到适应度曲线如图7所示，参数k与ε的最优量级与最优系数组合之后的结果如表8所示。

表8 参数自动寻优的滑模控制器主要性能指标及参数结果

从图7可知，在使用粒子群算法进行参数系数寻优，可使适应度值(速度增量)在有限迭代次数达到收敛，确定各参数在其量级下的最优系数。由表8可知，参数自主寻优过程可使滑模控制器中的各项参数的值稳定至小数点后多位，这是人为设置参数难以达到的精度；同时，对比表4可知，寻优器输出的速度增量变化与误差初始值的大小成正比，符合一般性。此外，为验证寻优器性能，针对表4序号1的数据做了50次测试，得出系数寻优策略的速度增量变化如图8所示。

图8 速度增量50次测试(表4序号1数据)Fig.8 Speed increment test,50 times (No. 1 data,Table 4)

结果说明，粒子群算法的随机性导致适应度值中的速度增量并不唯一(即系数组合不唯一)，但始终在平均值附近波动，并未出现不合理的结果，进一步验证了系数寻优策略的有效性与稳定性。最后，将表8中序号为1的6个参数代入滑模偏差控制器，最终得到的位置误差曲线、速度误差曲线如图9～10所示。

图9 位置误差曲线(表8序号1数据)Fig.9 Position error curve (No.1 data,Table 8)

图10 速度误差曲线(表8序号1数据)Fig.10 Speed error curve (No.1 data,Table 8)

综上，使用本文提出的量级/系数组合参数自主寻优器，可以优化滑模控制器手动且无规律参数设置步骤，输出粒子群算法优化的最优量级/系数参数组合。进一步，该控制参数组合下的滑模偏差控制器能够使相对位置和速度误差在规定时间和误差允许范围内达到收敛；同时，结合图7～8进行分析，以速度增量降低方向作为评价标准的参数自主寻优器，能够在有限迭代次数内收敛，说明该参数自主寻优器满足了燃料最优的要求。

6 结论

本文提出的时间与燃料约束的参数自主寻优变轨滑模控制算法，具有较强的抗干扰能力，通过建立参数量级与系数的寻优规则，自主配置控制参数，实现滑模的燃料最优控制。该方法融合了相对运动方程与指数趋近的滑模控制，并结合能量最优的轨迹规划器确定了具体的收敛时间，实现有效避障；其次，分析各控制参数的量级选取约束条件，制定了量级寻优的规则；然后，结合惯性权值优化的粒子群算法，限制适应度函数与最优系数更新规则；最后，输出最优量级与系数组合的控制参数，实现有限时间收敛的燃料最优滑模控制。通过仿真测试，本文方法输出的控制参数组合可使整个控制过程稳定收敛、且燃料消耗少。