充液航天器质量特性计算方法研究

李青，黄俊，缪远明，于杭健

北京空间飞行器总体设计部，北京 100094

1 引言

运载火箭、人造地球卫星、深空探测器、载人空间站等现代航天器通常都是充液系统，携带着大量的液体推进剂以及其他液体工质，其中的液体质量均占总质量的一半以上。充液系统可分为全充液系统和部分充液系统。全充液系统中的液体无自由液面，例如加压状态的囊式贮箱、金属膜片贮箱或满箱状态的表面张力贮箱等；而部分充液系统中的液体由于自由液面的运动，还存在晃动的问题，例如充液比(即充液体积与贮箱容积之比)小于1的表面张力贮箱或未加压的金属膜片贮箱等。

对于充液系统中液体晃动问题的研究始于20世纪60年代，研究方法主要有解析法、数值法和试验法。Abramson[1]系统介绍了几种特殊形状(包括矩形、圆柱形、圆环形等)容器内液体横向小幅晃动的基本理论和解析解。Levin[2]给出了直角圆锥容器内液体横向晃动的解析解。Hasheminejad等[3]分析了横放圆柱形容器内液体横向晃动问题。实际上，只有少数几种形状容器内的液体横向晃动问题可进行解析求解。Aslam[4]采用有限元法研究了地震导致的轴对称容器内的液体晃动；Wang等[5]在对液体晃动模态进行有限元数值分析的基础上，研究了晃动阻尼的计算方法；Gedikli等[6]采用边界元法进行液体晃动模态分析，并应用该方法研究了带防晃板贮箱内的液体晃动问题。计算流体动力学(CFD)方法是一类求解Navier-Stokes方程组的数值方法，包括有限差分法[7]、有限体积法[8-9]等。试验法[10-13]是验证数值计算正确性的有效途径。欧空局于2005年发射了一颗液体晃动试验卫星[14]——Sloshsat FLEVO，用于验证其基于有限体积法开发的CFD数值计算程序Comflo的有效性[15]。He等[16]采用有限体积法研究了油罐车内自由油面在刹车、加速、减速等工况下产生的晃动压力，并通过了试验验证。在航天器动力学分析和控制系统工程设计中，通常采用简单高效的等效力学模型计算来替代复杂费时的晃动流场计算，如单摆模型[17-18]、弹簧-质量模型[19]、MPB(运动脉动球)模型[20-21]等，从而可以比较容易地将液体晃动动力学方程整合到航天器系统动力学方程中。

无论是全充液系统还是部分充液系统，当研究其转动或姿态动力学时，必须对其惯性张量进行计算。Dodge[22]给出了矩形贮箱内液体转动惯量的解析解以及圆柱形贮箱内液体转动惯量的数值解曲线；马斌捷等[23-24]分析整理了航天器圆环筒形平底贮箱内液体有效转动惯量计算方法，研究了纵向挡板和横向挡板对液体转动惯量的影响。Lee[25]采用半解析方法计算了椭圆形、矩形、六边形和八边形全充液贮箱内液体的转动惯量。

综上，关于充液系统的已有研究文献主要侧重于液体晃动问题，对于液体质量特性的计算，特别是惯性张量的计算研究较少，且主要局限于若干特殊形状的贮箱，计算方法没有通用性。实际上，充液航天器质量特性的计算在工程中还没有得到足够的重视。在航天器设计中，通常将液体当作等量等分布的固体计算惯性张量，这种固化液体的简化计算方法显然是不符合实际情况的，会加大质量特性参数的偏差范围，从而增加动力学模型的误差和控制系统设计的难度。本工作采用势流理论推导了任意形状贮箱内的液体质量特性，采用有限元方法建立了计算液体质量特性的数值算法，通过一个矩形贮箱的算例验证了算法的正确性，将该方法应用于充液航天器质量特性的计算，研究了不同的液体处理方法对计算结果的影响，以期为充液航天器质量特性计算方法的选用提供参考。

2 理论推导

如图 1所示，O0-XYZ为惯性坐标系，O-xyz为充液系统本体坐标系，Ω为液体内部，Sf为自由液面，Sw为贮箱壁面，g为重力加速度。

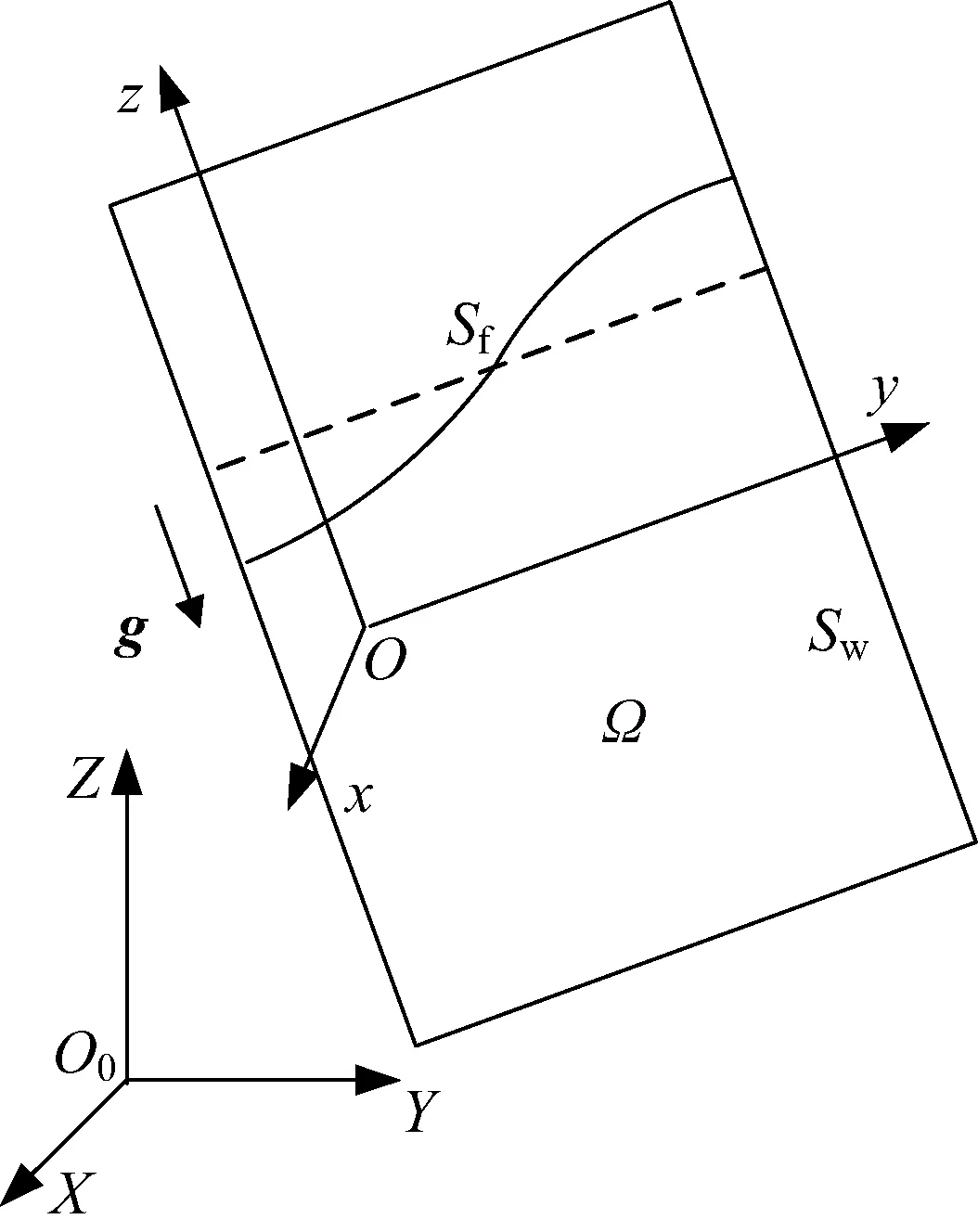
图 1 充液系统示意Fig.1 Illustration for liquid-filled system

当充液系统运动时，相对O点矢径为r的液体质点的绝对速度v等于该点牵连速度与相对速度u之和，即

v=vO+ω×r+u

(1)

式中：vO和ω分别为O点速度和系统的刚体角速度。假设贮箱内的液体是无粘、无旋、不可压缩的，则根据势流理论存在速度势Φ，使得v=∇Φ；在重力或惯性力加速度占主导、液体晃动幅度较小、液体表面张力可忽略时，Φ在Ω内满足

ΔΦ=0

(2)

Φ在Sw上满足

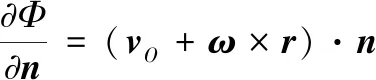
(3)

式中：n为单位外法线矢量。Φ在Sf上满足

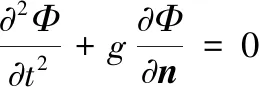
(4)

式中：t为时间。Φ具有如下形式：

(5)

式中：ψ为Stokes-Zhukovskiy矢势；φi为第i阶液体晃动模态函数；qi为第i阶液体晃动模态广义坐标。

Δφi=0

(6)

φi在Sw上满足

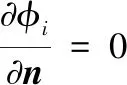
(7)

φi在Sf上满足

(8)

由方程(6)～(8)可解出φi及相应的固有频率ωi。

ψ在Ω内满足

Δψ=0

(9)

ψ在Sw∪Sf上满足

(10)

假设液体的密度为ρ，液体的动能可以写成

(11)

将式(1)代入式(11)，并根据拉格朗日方程推导出

(12)

(13)

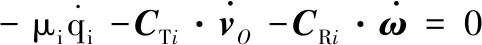
(14)

式中：m为液体总质量；rc为液体质心位置矢量；CTi为第i阶液体晃动与贮箱的平动耦合系数矢量；Fd为液体对贮箱的动作用力矢量；J为液体等效刚体关于O点的惯性张量；CRi为第i阶液体晃动与贮箱的转动耦合系数矢量；Md为液体对贮箱关于O点的动作用力矩矢量；μi为第i阶液体晃动广义质量。它们的表达式如下：

(15)

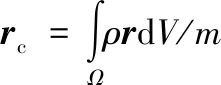
(16)

(17)

(18)

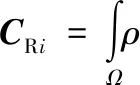
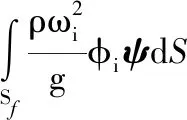
(19)

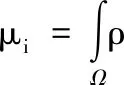
(20)

对于全充液系统，CTi、CRi和μi均为零，J即为液体惯性张量的理论表达式，由于没有自由液面，式(17)中略去Sf项。式(15)～(17)给出了全充液系统内液体质量特性的表达式。

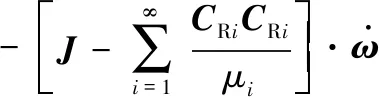
(21)

因此，部分充液系统内液体惯性张量的理论表达式为

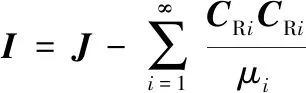
(22)

式(15)(16)(22)给出了部分充液系统内液体质量特性的表达式。

3 数值算法

采用三维有限元划分液体域网格，由第2节的理论推导可知，充液系统内液体的质量和质心位置可根据式(15)(16)进行数值积分得到，而惯性张量与ωi、φi和ψ有关，需要首先采用有限元方法得到它们的数值解。

方程(6)～(8)和方程(9)(10)可分别写成如下变分形式：

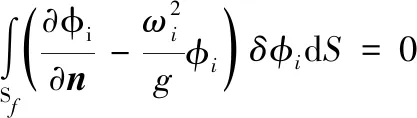
(23)

(24)

采用三维单元划分液体网格，在每个单元内场函数可以表示成

(25)

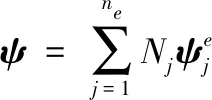
(26)

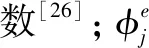
(27)

(28)

对式(27)(28)分别应用变分原理，得到

(29)

(30)

求解方程(29)的广义特征值问题得到ωi和φi的数值解。求解方程(30)的线性代数方程组得到ψ的数值解。然后再根据式(17)(22)进行数值积分，分别得到全充液系统和部分充液系统的惯性张量。

4 验证算例

如图2所示，对于长为a、宽为b、液高为h的矩形贮箱液体，本体坐标系原点O位于液体质心，根据文献[22]的推导，其液体转动惯量的解析解为

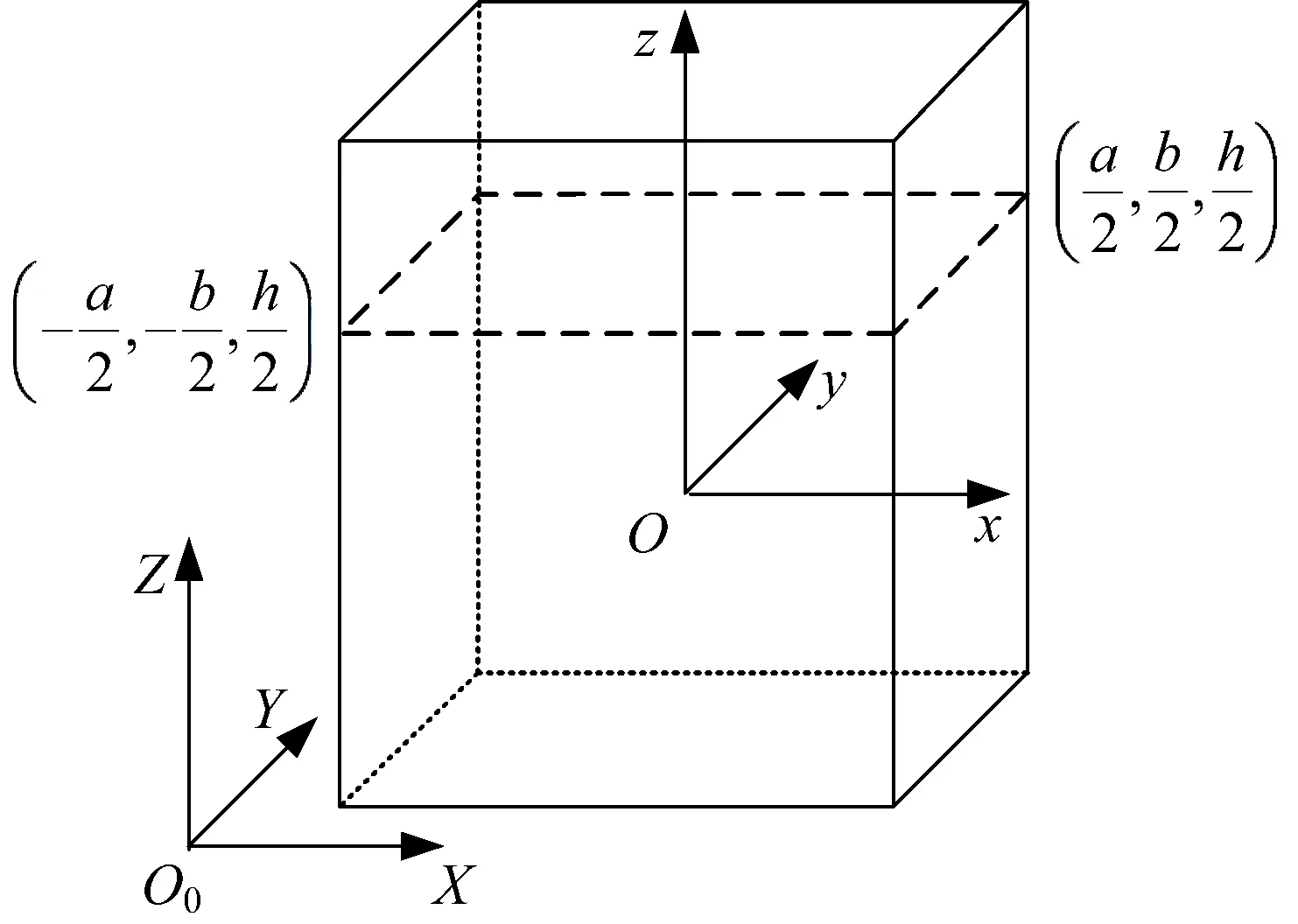
图 2 矩形贮箱示意Fig.2 Illustration for a rectangular tank

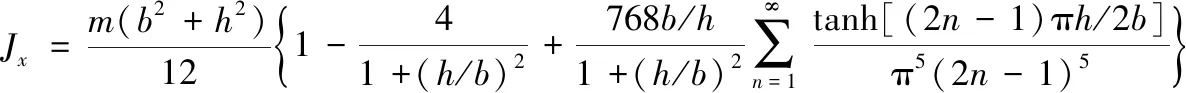
(31)

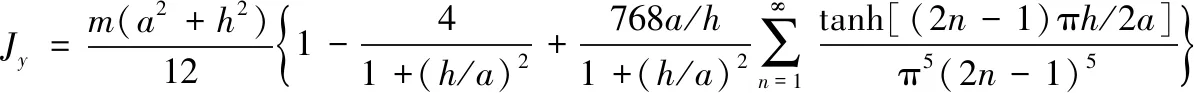
(32)

(33)

若存在自由液面，则液体转动惯量的解析解为

(34)

(35)

Iz=Jz

(36)

在本验证算例中，取a=2.11 m、b=1.33 m、h=1.1 m，液体为水。如图 3所示，液体有限元模型划分为20 400个十结点四面体单元，总结点数为29 842。对于部分充液状态，在计算Iy时截取了如图 4所示的前3阶x向液体晃动模态，在计算Ix时截取了如图 5所示的前3阶y向液体晃动模态。

图3 矩形贮箱内液体的有限元模型Fig.3 Finite element model for the liquid in a rectangular tank

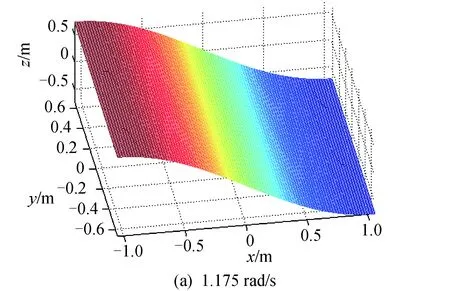
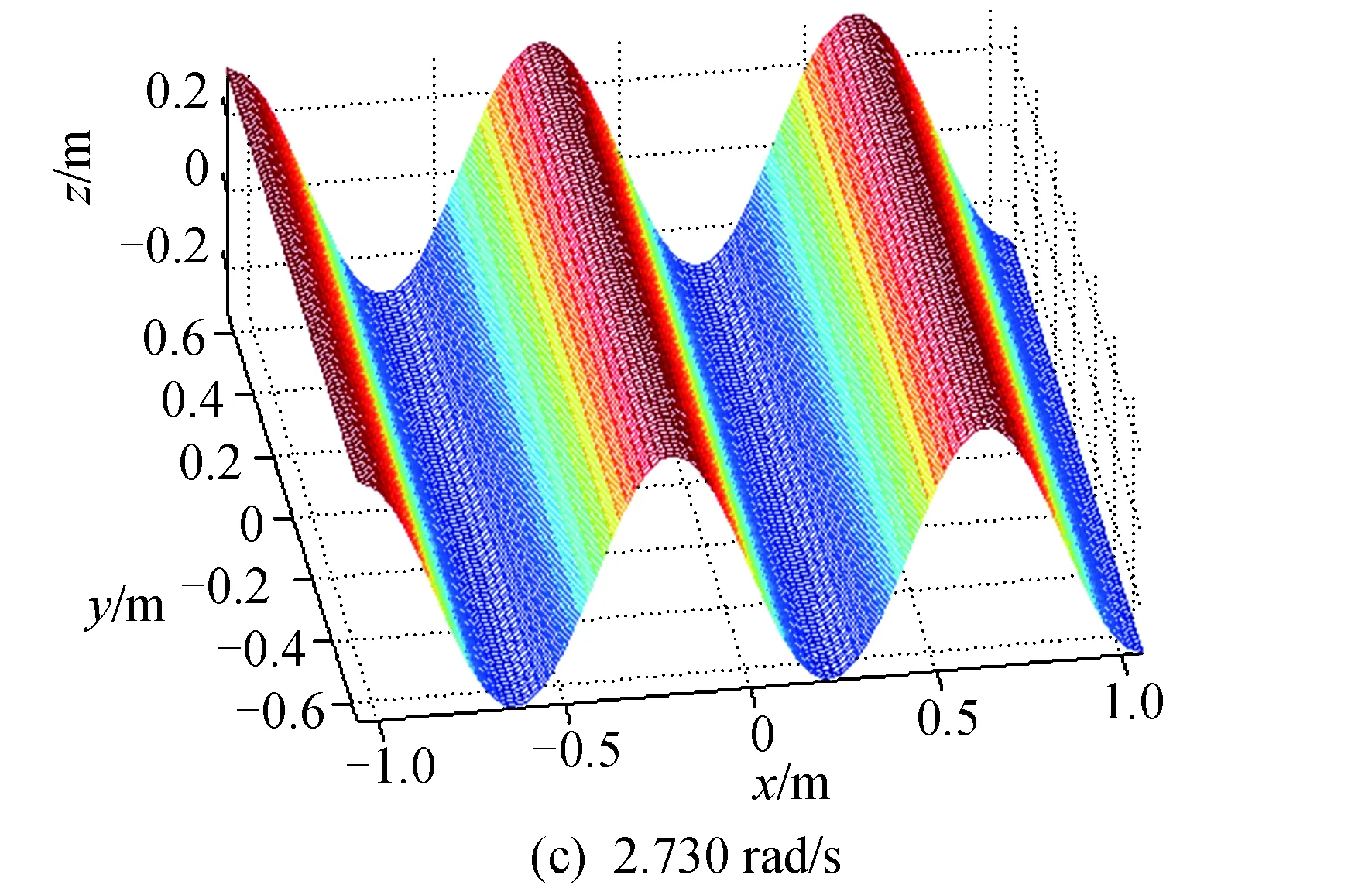
图4 沿x轴方向的前3阶液体晃动模态振型Fig.4 First three sloshing mode shapes along x-axis

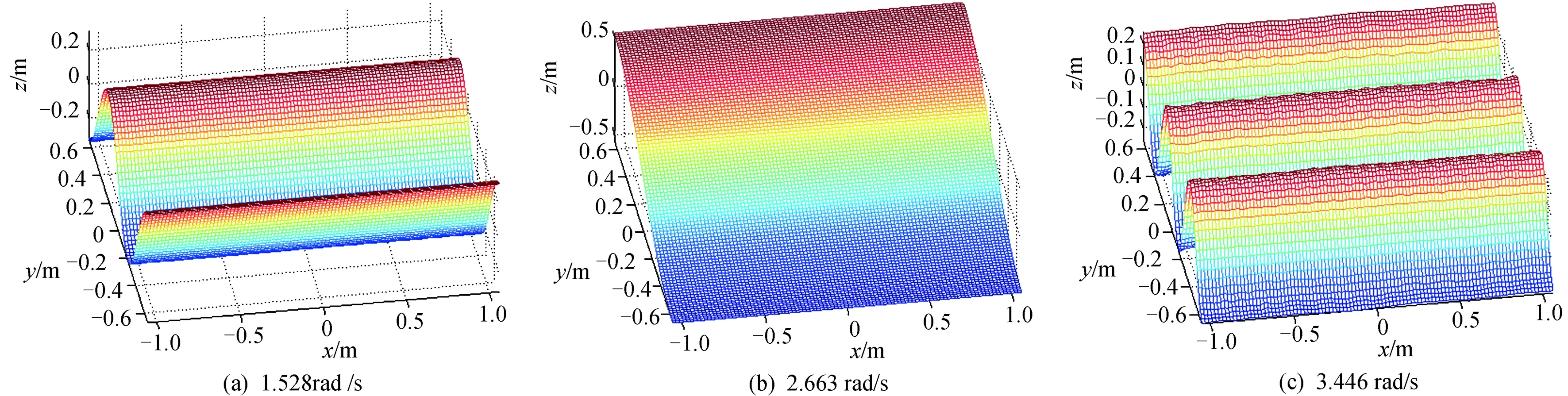
图5 沿y轴方向的前三阶液体晃动模态振型Fig.5 First three sloshing mode shapes along y-axis

表 1对比了液体质量特性的数值解与解析解的计算结果，可见数值解与解析解的相对误差非常小，从而验证了本文数值计算方法的正确性。由于矩形贮箱内液体关于其质心的惯性主轴始终为x轴、y轴和z轴，故所有的惯性积计算结果均为0且未在表1中列出。

表1 液体质量特性的数值解与解析解对比

5 应用研究

某充液航天器及其坐标系定义如图 6所示，OP-XPYPZP为机械坐标系，OPC-XPCYPCZPC为质心坐标系(由机械坐标系绕XP轴旋转45°并平移得到)，OPC为航天器质心；推进剂贮箱为球形金属膜片贮箱，包括2个氧化剂贮箱和2个燃烧剂贮箱，两两对称布置。根据质量特性测量结果，该航天器干重状态下的质量特性如表 2所示。

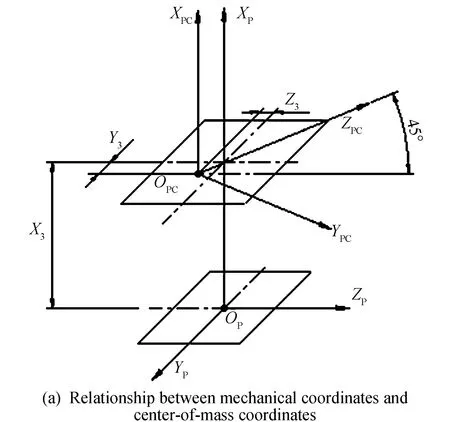
图6 某充液航天器及其坐标系定义Fig.6 Illustration for a liquid-filled spacecraft and its coordinate systems

表2 航天器干重状态下的质量特性

氧化剂密度为1445.1kg/m3，加注质量为249.24 kg；燃烧剂密度为874.1 kg/m3，加注质量为150.76 kg。建立推进剂贮箱内液体的有限元模型，如图 7所示。根据表 2数据和本文方法可以计算出该航天器充液状态下的质量特性，如表 3所示。其中，金属膜片贮箱加压状态对应全充液工况，未加压状态对应部分充液工况。与传统的“固化液体”处理方法计算结果相比，由本文方法计算出来的转动惯量明显减小，全充液工况最多减小4%，部分充液工况最多减小16%；而不同方法给出的质量和质心位置计算结果都是相同的。

图7 充液航天器推进剂贮箱内液体的有限元模型Fig.7 Finite element model for the liquid in a propellant tank for a liquid-filled spacecraft

表3 航天器充液状态下的质量特性

6 结论

本文基于势流理论推导了任意形状贮箱在全充液和部分充液两种状态下液体质量特性的一般表达式，建立了计算液体质量特性的有限元数值方法；通过矩形贮箱液体质量特性数值解与解析解的对比，验证了计算方法的正确性；对于布置多个推进剂贮箱的充液航天器，分别采用“固化液体”方法和本文方法计算了它的质量特性。研究表明，部分充液状态下的转动惯量低于全充液状态下的转动惯量，而两者均低于固化液体状态下的转动惯量。本文方法有助于提高充液航天器质量特性计算的准确性。除航天器外，所提出的方法亦可用于航空飞行器、油罐车、液货船等其他充液系统质量特性的计算和研究。