低太赫兹频段ITU大气吸收模型伪线谱的修正研究
2021-09-02宋俊元富子豪赵雄文耿绥燕
宋俊元 富子豪 赵雄文 耿绥燕
(华北电力大学,北京 102206)
引 言
随着5G的商用落地,6G的研究也在国内外兴起. 根据Molisch等人[1]和ITU[2]的展望,未来6G将更着重考虑高保真全息社会、万物互联、时间敏感三个方面的应用,主要应用场景有全息通信、触觉网络、网络与计算融合、极高速信息流、万物互联、片上通信、天地融合等[1]. 这也使得6G相较于5G有着更高的关键性能指标要求[3]. 而太赫兹频段(300 GHz以上)、亚太赫兹频段(100~300 GHz)频谱资源丰富、带宽大、波束窄、保密性强、抗干扰等特点,使其成为6G的重要组成部分[3],以应对爆炸式增长的移动数据需求.
然而,实现太赫兹频段通信还存在诸多技术挑战. 在太赫兹设备技术发展的同时,许多工作也集中在太赫兹信道、新的调制编码方案、太赫兹信号空间复用等方面[3]. ITU-R第228-3/3号课题指出,275 GHz以上频率电信系统的规划和设计急需更好的传播模型[4]. 随着频率的升高,太赫兹波的传播受到大气吸收的影响也越来越大,一个准确、计算方便的大气吸收模型对太赫兹频段路损估计、信道建模[5]以及对6G太赫兹频段通信系统的设计与规划等都至关重要.
根据分子响应理论(molecular response theory,MRT),分子吸收的能量主要来源于分子的轨道能、转动能、振动能这类量子化的能量,其值是离散的.而根据量子理论,其能量关系对应于分子的吸收或发射光谱,对于电磁波在大气中的传播即是分子的逐线吸收部分[6-7]. 另一部分则来源于分子所具有的平动能,代表分子移动的能量. 这个能量是非量子化的,其取值可以是连续的,对应分子的连续谱吸收[6,8].
电磁波在大气中传播时,会受到离散的分子线谱与连续的水汽吸收连续谱影响. 除此之外,由于大量气体分子在空间中会受到气压、量子效应等影响,会造成分子吸收线谱展宽. 常见的展宽种类包括海森堡(Hersenberg)时间和能量不确定性关系造成的自然展宽、由分子间碰撞造成的碰撞展宽、分子运动的多普勒效应导致的多普勒展宽等. 在微波区域自然展宽可以忽略不计,多普勒展宽主要发生在气压较小的大气层顶部,而在低层大气,分子间碰撞造成的碰撞展宽占主要地位[8].
哈佛大学史密斯天体物理中心开发维护的分子吸收数据库收纳了大量分子光谱参数,其综合了业界对此开展的各实验以及研究,对于分子的线谱数据有着详细的记录[9]. 史密斯天文台利用HITRAN(High-resolution Transmission)数据库,基于MRT开发了大气模型(atmosphere model,AM)[10]. AM本质是一个MRT的计算工具,通过计算大气中氮气、氧气、二氧化碳、水汽等的逐线吸收,以及MT_CKD(Mlawer–Tobin-Clough–Kneizys–Davies)水汽连续谱模型,综合给出0~10 THz电磁波在大气中的吸收衰减曲线.
工程中,更常用ITU-R P.676大气吸收模型,其利用7个参数对大气分子吸收线谱进行描述[11]. 对于水汽的连续谱ITU模型则将其拟合为1 780 GHz处的一条伪线谱(pseudo-line,PL),利用其远翼效应的拖尾来表示. 然而,现有ITU模型并不完善. 文献[12]指出,对于600 GHz以上的太赫兹频段,ITU模型给出的大气吸收特征衰减比MRT理论的结果要高出很多. 这将会限制ITU模型在未来6G对低太赫兹频段的使用.
本文以MRT为基准,利用多目标参数拟合方法,为ITU模型拟合了一条新的连续谱PL. 以频率、湿度为自变量设定多个目标函数联合优化,使ITU模型给出的经验大气吸收计算结果更接近MRT给出的大气衰减. 本文的研究结果可以减小ITU模型在低太赫兹频段的误差,为后续6G宽带连接新频谱提供了高精度的、方便的大气吸收衰减计算模型.
1 典型模型分析
常见的大气吸收模型可以分为三种:第一种是纯经验模型,其利用多项式等方法拟合出大气衰减,例如ITU-R P.676-8的附录2中给出的多项式计算模型[13]以及文献[14]中给出的100~450 GHz大气吸收模型. 第二种是基于物理能量的模型,也即是基于MRT的大气吸收模型. 其本质是计算复杂的MRT,一些研究也开发了相应的计算软件,例如AM、通用大气辐射传输软件等[15]. 第三种是半经验模型,如ITU-R P.676-11、12等,其给出简化的线谱参数,同时也将水汽连续谱拟合为水汽在1 780 GHz处的一条线谱,再一并进行逐线积分计算出大气吸收衰减. 经验模型计算量较小,但受限于函数形式,常用于计算较短的特定频段内的衰减. MRT模型描述准确,能很好地解释实验测量结果,可以用于计算较大频段内的衰减,但需要保存大量的分子光谱数据. 且对于不同气压、分子种类等环境条件,按需选取不同展宽线形等再与线谱乘积积分,使其计算量偏大、计算程序占用空间大,在工程应用中具有一定局限性. 半经验的ITU模型在利用逐线积分的计算形式基础上给出经验的光谱参数,提升了精度的同时也一定程度上减小了计算量.
ITU模型主要基于Liber的MPM93模型[16],利用光谱参数以及统一的展宽线形对氧气和水汽分子线谱逐线积分来计算电磁波大气衰减,水汽的连续谱则被拟合为1 780 GHz处的一条线谱产生的远翼拖尾. 马德里研究中心的Pardo等人在文献[7]中指出,PL与实际的连续吸收谱一致性较差. 同时Pardo还认为,在毫米波等频段,虽然由压力碰撞造成的展宽是主要因素,可以用J. H. Van Vleck和V.E. Weisskopf给出的VVW展宽线形来描述,但是并不意味着在0~1 000 GHz内计算大气衰减可以全部使用同一种展宽线形,所以提出要考虑多种因素造成的展宽并相应地选用适配的展宽线形[7]. 表1总结了文献[8]和文献[10]给出的几种常见的展宽线形,以及它们的适用情况.
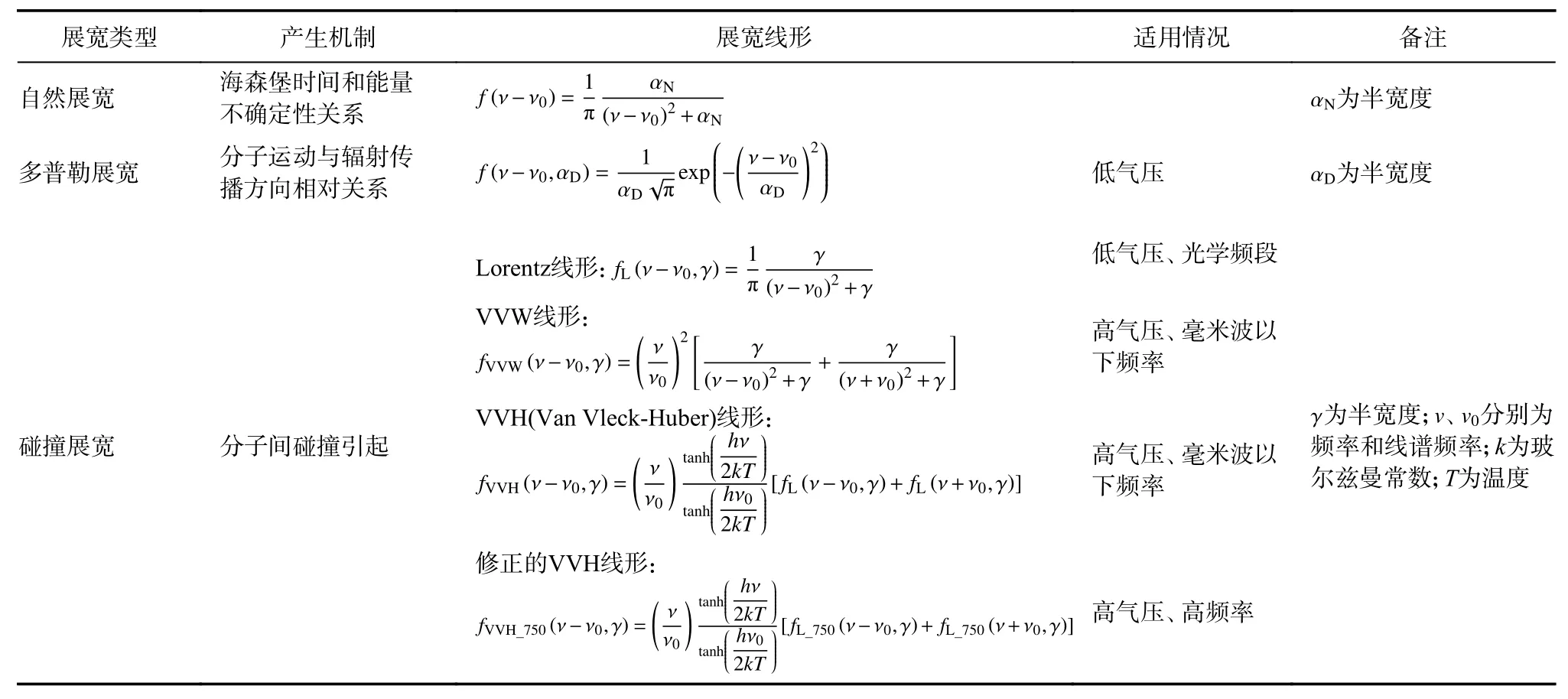
表1 谱线展宽与展宽线形[8, 10]Tab. 1 Spectral line broadening and line shape
本文对于ITU模型使用的有ITU-R P.676-11和ITU-R P.676-12两个版本,以下分别简称为ITU(11)、ITU(12). 两个版本对电磁波大气吸收特征衰减与地面传输衰减计算方法一致,仅ITU(12)对光谱参数集进行了修订. 根据ITU模型,大气吸收衰减可通过如下模型进行计算:

式中:S i、Fi分别代表第i条线谱强度和对应的线谱展宽;为 氮气吸收和氧气的Debye谱;f为频率,单位为GHz;p为干大气压强,单位为hPa;e为水汽分压,单位为hPa;T为温度,单位为K.
基于MRT的大气吸收计算工具−AM已开发出相关程序,依照特定输入格式输入大气分层结构及各层对应的温度、压强、高度等,即可输出透过率、大气衰减等结果,本文以AM计算结果作为MRT导致的大气吸收结果. 由于AM基于物理的特点,其需要保存大量的分子光谱参数使得程序占用空间较大. 同时其输入格式较为复杂,运算过程中还需要依据不同的大气环境情况综合选择展宽线形等,使得程序本身较为复杂,不易于工程使用.
一些文献报道了在低太赫兹频段ITU模型相比MRT计算结果误差较大,如文献[12]指出ITU(11)版本与基于MRT理论的计算在太赫兹频段相差较大. 除此之外,最新修订的ITU(12)版本对大气分子光谱参数进行了修正,但对于文献[12]所提到的误差较大问题依然存在,具体如下.
图1给出了大气压强p=1 013.25 hPa、温度Tc=15 °C、空气含水量ρ=7.5 g/m3时(下文如无特指,气压温度等均为此参数),ITU(11)、ITU(12)模型与AM的太赫兹波特征衰减. 可以看出:对平坦部分,0.6 THz内AM与ITU模型差别较小,而0.6 THz至1.0 THz差别逐渐增大. 特别的,对于误差较小的ITU(12),在窗口W1中的0.669 THz处衰减为61.82 dB/km,大于AM给出的56.71 dB/km;在窗口W2中的0.85 THz处衰减为77.27 dB/km,远大于AM的64.5 dB/km. 在窗口W2, ITU(11)绝对误差达到20 dB/km以上,ITU(12)也接近15 dB/km.
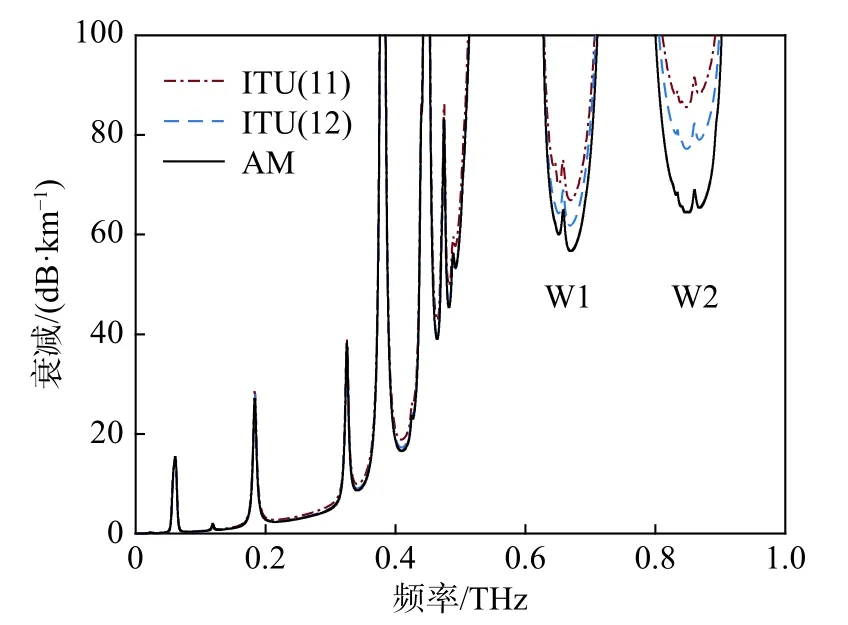
图1 ITU模型与AM对比Fig. 1 Comparison between ITU model and AM
除此之外,在峰值附近存在绝对误差较大的情况. 这是由于MRT根据大气中具有不同特点及不同分子组分,依据先前的实验研究采用不同展宽线型,例如对二氧化碳、单分子氧、氮氧化物等采用Gross展宽,对结合氧分子采用结合的VVW展宽,以及对水汽采用VVH展宽谱线[3]. 而ITU模型为了实现计算的方便,统一使用了一种展宽谱线,这使得吸收曲线在线谱附近会产生较大的不同.
2 ITU PL拟合
ITU模型可看作1 THz以内逐线积分与以PL代替的水汽连续谱之和;AM则为15 THz以内逐线积分与真实水汽连续谱之和. 在ITU模型所适配的0~ 1 THz内,可以将AM看作是1 THz以内逐线积分、1 THz以上远翼效应、真实水汽连续谱三者之和.
从MRT来看,造成逐线积分+连续谱的物理计算模型与ITU模型不同的原因在于:1)大于1 THz线谱对小于1 THz衰减的远翼影响;2)水汽的连续谱吸收问题;3)逐线吸收所选用的展宽线形不同带来峰值附近差异较大的问题.
本文认为,对于工程实用的半经验模型来说,并不一定要完全按照MRT来构建,故可以将1 THz以上远翼效应和水汽连续谱以一个函数Δ代表. 此时,Δ即等于AM计算结果减去ITU模型中1 THz以内逐线积分的部分.
图2给出了ITU(12)模型中给出的PL与函数Δ的关系. 由图2可见,ITU模型与AM的不同是由于PL在大于0.5 THz频段产生了过高的计算值. 显然,ITU模型中1 THz逐线积分部分与Δ之和即等价于AM. 此时,Δ即是需要拟合的新伪线谱(new pseudo-line, nPL).

图2 PL与Δ的对比Fig. 2 The comparison of pseudo-line(PL) and Δ
2.1 目标函数的确立
对于ITU模型,若以整体最小均方误差(meansquare error,MSE)作为目标函数会造成新结果极大地提高较低频率误差以减小较高频率误差的问题,使得拟合结果不符合本文“尽量不增大较低频段误差”的前设要求. 因此,本文将目标函数分段成三部分,在确保整体均方绝对误差最小的同时,将300 GHz以内的较低频段与300 GHz以上的低THz频段分段考虑,构成多目标函数的联合优化问题. 针对ITU模型待优化参数较多、数据段较长等特点,本文对MSE做了一些形式上的改变,目标函数如下:

式中:F为目标函数,单位为dB;HR为相对湿度,取值为0%~100%;L为待拟合曲线,单位为dB;f为频点,单位为GHz,由于Δ存在“毛刺”现象,为避免局部极大/极小值对参数优化拟合的影响,故f在较为平滑的频段中取值;Nf为所去频段中频点个数. 三个目标函数形式相同,频率fSub300GHz、fLowTHz、fTotal分别为0~ 300 GHz、300~ 1 000 GHz、0~ 1 000 GHz. 同时,为保持目标函数和ITU模型单位上的一致,Δ、MSE均以dB为单位.
2.2 nPL优化拟合
根据前述的拟合问题,假设与多个目标函数建立,此时拟合问题可转化为多目标函数的优化问题:

式中,fPL和bm是ITU形式的线谱定义. ITU模型对每一条谱线利用7个参数加以确定,即fPL表示PL所在的频率;系数b1,2,3确定出线谱强度;系数b4,5,6则给出线谱展宽的半宽度.
本文利用多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)算法,以得到优化问题Q1的最优解. MOPSO算法先随机生成一系列粒子,并计算各个粒子对应的目标函数大小,选取一定数量的非劣解加入到精英集(即每一次迭代过程中的非劣解集)中. 对于一个粒子,其对应的多个目标函数值中有任一个优于当前个体极值对应的目标函数值的即可认为是非劣解;当所有目标函数值都优于当前值即为优解;而所有目标函数均劣于当前值时即为劣解. 每一次迭代过程中优解直接替换原有个体极值,其余非劣解以50%的概率替换个体最优,劣解则以5%的概率初始化为新的粒子,以此规则不断更新粒子的个体极值和全局极值. 然后相应计算粒子的速度并更新位置. 同时不断选取非劣解加入精英集,精英集则不断检查内部解,根据适应度将较差的解剔除,最终精英集即可逼近优化问题的全局最优解.
本文建立了100个粒子种群以及200个粒子大小的精英集,设置惯性权重为0.729,个体极值、全局极值学习因子均为1.494 45,多样性系数为0.000 1,通过1 000次迭代给出一组较ITU(12)模型中现有PL更优的一组nPL参数,如表2所示.

表2 所提nPL参数Tab. 2 proposed nPL parameters
3 所提nPL评估分析
3.1 多目标优化的nPL与单目标优化对比
根据2.1节中的描述,多目标函数的建立在于确保整体均方误差最小的同时保证300 GHz以内频段与低THz频段的误差都能控制在较小范围内. 本节给出所提nPL与以整体均方误差为唯一目标函数的拟合曲线对比. 此单目标函数拟合问题可以表示为:

式中变量定义与公式(8)相同.
通过常见的单目标函数的优化算法,可以得到其拟合曲线. 图3给出了所提nPL与PL以及Δ的对比,并给出对单目标函数优化问题Q2的拟合曲线.可以看出:本文所提nPL在400 GHz以内与ITU(12)PL基本相同,但在800 GHz以内更贴近Δ;Q2拟合曲线虽然在600~900 GHz显示出较好的拟合结果,但在0~500 GHz内却远远偏离Δ. 显然,多目标函数优化问题Q1的拟合曲线较单目标函数Q2问题的拟合曲线在较低频率范围内的误差更小. 而900 GHz后,无论是所提nPL还是Q2拟合曲线都存在一定程度的低估衰减的情况.
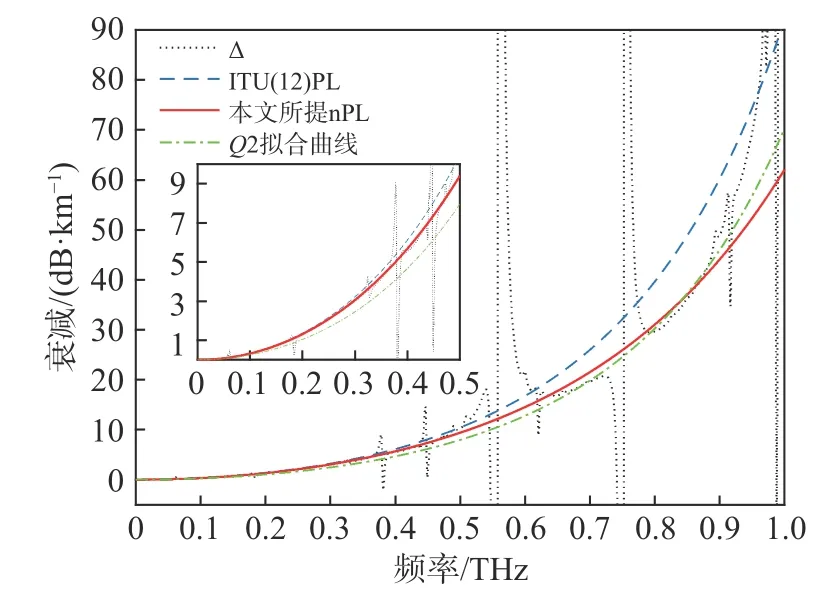
图3 所提nPL与ITU(12)PL、Q2拟合曲线、Δ对比Fig. 3 Comparison between proposed nPL, PL of ITU(12),Q2 fitting curve and Δ
3.2 所提nPL与AM对比
所提nPL的ITU模型与AM的整体特征衰减对比由图4给出. 显然,所提nPL的ITU模型较ITU(12)更接近AM的计算结果. 从图4可以看出:800 GHz以内所提模型与AM结果基本吻合,只在900 GHz附近出现小的差别;在900~1 000 GHz大约存在10 dB误差.

图4 所提nPL的ITU模型与其他模型对比Fig. 4 Comparison between ITU of the proposed nPLmodel and other models
分频段的误差分析与性能改善情况在表3中给出. 所提nPL的ITU模型与ITU(12)在600 GHz以内相对误差变化不大,稳定在2%以内;600~900 GHz内所提nPL的ITU模型误差得到了有效降低. 特别是600~ 700 GHz从原有的5.54%降到1.38%,800~ 900 GHz内更是降低了14.47%. 虽然所提nPL的ITU模型在900~ 1 000 GHz内误差有些许提升,但由于900 GHz以上大气特征衰减急剧增大到100 dB/km以及现阶段受到太赫兹半导体技术的功率限制等因素,未来6G使用频段仍然主要集中在衰减较低的低太赫兹频段,特别是各大气衰减窗口处. 故用900 GHz以上3.75%的误差损失以换取900 GHz以内,尤其是600~900 GHz频段内两个超大带宽窗口处的误差极大降低,具有实际工程意义.

表3 所提nPL的ITU与ITU(12)的误差对比Tab. 3 Error comparison between ITU model of the proposed nPL and ITU (12)
3.3 温度、气压影响分析
不同温度、气压情况下,所提nPL的ITU模型与ITU(12)模型的三个典型段目标函数如图5所示.对于整体0~1 000 GHz和低太赫兹300~1 000 GHz频段,相较于ITU(12)模型,所提nPL显著提升了ITU模型相对物理模型的MSE. 对于气压范围0.6~1.0个标准大气压(atm)内,所提nPL的ITU模型其修订MSE的目标函数F均明显低于ITU(12)模型,二者的差值即代表所提nPL较ITU(12)的MSE提升. 同时图5也显现出,ITU模型对温度的变化较为敏感,而本文所提nPL的ITU模型在15 °C时MSE远小于ITU(12)模型. 同时注意到,在0~300 GHz所提nPL存在一定程度上MSE增大的情况,这与表3中结论一致. 并且此性能损失随着温度远离15 °C而增大,但是其损失的性能相较于全频段(0~ 1 000 GHz)以及低太赫兹频段(300~ 1 000 GHz)要小一个数量级左右.

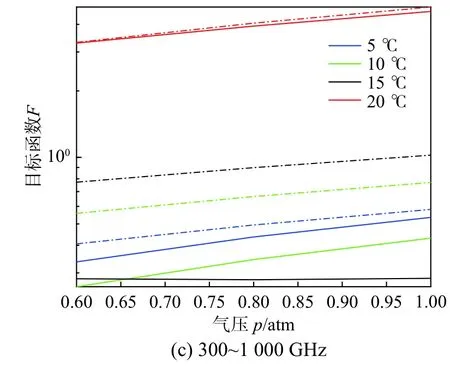
图5 不同温度、气压情况的目标函数Fig. 5 The objective function of the model at different temperatures and pressures
4 结 论
本文首先建立ITU模型与基于MRT的AM的关系,然后引入差值Δ(即待拟合曲线),后利用MOPSO算法对Δ进行系数拟合,进而给出了一条符合ITU模型形式的nPL,使得ITU模型的结果更接近于基于MRT计算的结果. 所提nPL的ITU模型相较ITU(12)计算结果在600 GHz以内的差别在2%以内,而在600 GHz以上频段误差至多减小了14%. 虽然在900 GHz以上频段带来一定的性能损失,但结合6G使用频段,所提nPL的ITU模型在600~900 GHz段内两个超大带宽窗口处的误差极大降低,具有实际工程意义. 根据不同温度、大气压强下模型性能曲线,所提nPL的ITU模型对温度变化较为敏感. 在5~20 °C、0.6~1.0 atm条件下,其目标函数在0~1 000 GHz与300~1 000 GHz内有100数量级的优化. 本文提出的nPL不仅在形式上符合现存ITU模型形式,还提供了更精确的大气吸收衰减值,对未来太赫兹波的传输建模、仿真分析及系统设计均有指导意义.
