基于奇异值分解的空域海杂波抑制算法

王龙岗 岳显昌 吴雄斌 易先洲

（武汉大学电子信息学院，武汉 430072）

引 言

短波波段垂直极化的电磁波沿海洋表面传播时具有衰减小且能够绕射传播的特点，因此高频地波雷达(high frequency surface wave radar, HFSWR)可克服地球曲率的影响，实现对海洋表面和低空目标的超视距、全天候探测，具有探测范围广、成本低、实时性好等特点，成为探测海面和低空目标的重要手段[1].

HFSWR进行目标探测时，除了目标回波信号外，回波当中还存在大量的干扰信号，其中由海浪散射产生的回波信号称为海杂波. 回波中一阶海杂波的强度往往比目标信号强得多[2]，而且舰船等低速目标的多普勒频率与海杂波的Bragg峰相近，从而被淹没在海杂波中，很难被检测到[3]. 因此对海杂波进行抑制，是HFSWR实现对一阶海杂波谱中目标检测的关键.

目前，HFSWR检测舰船目标的方法主要有海杂波对消法和现代谱估计方法[4]. 其中海杂波对消方法包括基于模型的对消方法、循环对消方法和预测对消方法. 基于模型的对消方法是通过对海杂波进行建模，然后将利用模型得到的海杂波作为背景，进行对消处理[5-6]. 这种方法要求建立的模型与真实的海杂波特性较好地吻合，否则无法达到理想的效果. 循环对消方法主要有Root[7]、郭欣等[8]提出的基于快速傅里叶变换(fast Fourier transform, FFT)的幅度、相位分析的对消方法和基于扩展Prony算法的循环对消算法[9]. 预测对消法[10]是借助神经网络通过数据训练来提取海杂波的参数，进行海杂波对消. 循环对消法和预测对消法是将海杂波的主要分量近似看作正弦信号，估计对应的频率、幅度和相位等参数，对消强的海杂波及其谐波分量. 现代谱估计方法主要有小波变换法和基于子空间估计的海杂波抑制算法.在小波变换方法中，基函数的选择对抑制效果有较大的影响，需要选择合适的基函数才能得到较好效果，并且这种方法会破坏回波信号的相位信息[11-12].子空间估计法是根据杂波在子空间的聚集特性来实现海杂波的抑制，如基于特征值分解(eigen value decomposition, EVD)的方法[13]、基于奇异值分解(singular value decomposition, SVD)的方法[14-15]、改进特征值分解(modified eigen value decomposition, MEVD)的方法[16]. 这些基于子空间估计的海杂波抑制方法，只能在目标与海杂波多普勒频率差别较大的情况下实现海杂波的抑制. 当两者频率接近或者重叠时，目标会被误消，造成漏警. 而高阶奇异值分解(high order SVD, HOSVD)方法，从方位维、距离维和慢时间维三维联合来估计海杂波子空间，但是由于一阶回波的复杂性，不容易实现海杂波子空间与噪声子空间的准确划分，对海杂波的抑制效果不理想. 此外还有斜投影(oblique projection, OP)方法，在已知海杂波方位的情况下，通过空间OP来抑制海杂波[17]，然而在实际探测目标时，海杂波的方位无法预先得知.

针对上述问题，本文提出了基于SVD的空域海杂波抑制方法(以下简称空域SVD算法)，充分利用天线阵列的信息，在海杂波方位未知的情况下，通过SVD来估计空域的海杂波子空间和噪声子空间，然后利用子空间之间的正交性，通过投影实现在空间域对海杂波的抑制. 空域SVD算法是在空域对海杂波进行抑制的，一般来说距离-多普勒(range-Doppler,RD)谱中单个谱点信号源只存在有限的几个方位，在对阵列信号的协方差矩阵进行SVD时，得到的奇异值数目较少，比较容易准确划分海杂波子空间与噪声子空间，海杂波的抑制效果更好. 文中首先研究了HFSWR海杂波产生的机理，然后阐述了基于SVD的空域海杂波抑制算法的原理，最后利用仿真与实测数据对算法性能进行验证，并将结果与现有的空域海杂波抑制方法进行了对比，验证了本文算法的有效性.

1 海杂波形成的机理

海浪的运动状态是一种复杂和混沌的随机过程[18]，由不同频率、波高和传播方向的海浪叠加而成，这些海浪近似呈现正弦波动，如图1所示[4].干涉. 设海浪的波长为L，雷达发射电磁波的波长为

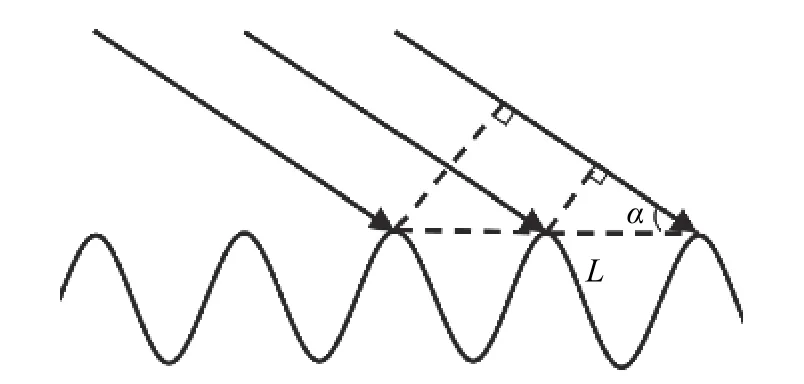
图1 海杂波形成机理Fig. 1 Formation mechanism of sea clutter

HFSWR发射的高频无线电波与海浪发生相互作用，使电磁波发生散射，散射的电磁波之间会发生λ，当电磁波束照射到图1所示的海浪上时，入射波到达海浪各散射点的路程差为Lcosα，当满足式(1)时，海浪后向散射产生的回波信号间的波程差为λ，回波信号同相加强，产生Bragg谐振：

式中，α为入射波的擦地角. 当α趋于0时，即当无线电波波长等于海浪波长的两倍时，发生Bragg谐振，在回波多普勒谱中产生两个尖峰，称为一阶Bragg峰.

根据深水区动力学原理，重力波的波长与流速之间满足：

海浪相对雷达站的径向速度为

Bragg峰对应的多普勒频率为

将式(1)、(2)和(3)代入式(4)可得

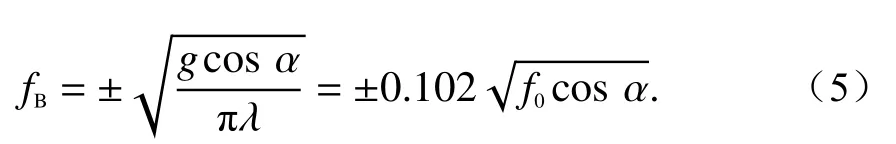
式中：g表 示重力加速度；fB表示Bragg峰的多普勒频率，单位是Hz；f0表示雷达工作的中心频率，单位是MHz；±是指海浪朝向和背离雷达. 通常雷达的擦地角α很小，式(5)可近似为

式中，fB表示Bragg峰的多普勒频率的理论值. 实际上由于海流的存在，实测的多普勒频率相比理论值会存在海流引起的多普勒频率fc左右的偏移，这是造成海杂波一阶谱展宽的重要原因. 因此，在对海杂波进行建模仿真的过程中，必须考虑海流的影响[19].

2 基于SVD的空域海杂波抑制算法原理

在一个积累周期内，对接收阵的每个阵元接收的回波信号进行傅里叶变换，得到对应的RD谱[20]. 不同距离、不同速度的散射源的回波信号将被分离开. 对于一阶谱中的目标，无法从距离维和多普勒维将其与海杂波区分开，考虑在空域对他们进行分离，并抑制海杂波.

2.1 信号模型

假设空间中有K个窄带远场信号s1(t),s2(t),···,sK(t)入射到如图2所示线性均匀阵列，设阵元的个数为N(N>K)，阵元间距为d，信号源的入射方向分别为ϕi(i=1,2,···,K)，其中前P个方位为海杂波的方位.N个阵元在t时刻的输出数据矢量为

式中：x(t)= [x1(t),x2(t),···,xN(t)]T；A表 示阵列流型，A=[a(ϕ1),a(ϕ2),···,a(ϕK)]，其中,，；s表示信号矢量，s=[s1,s2,···,sK]T，si表示第i个 信号源的复振幅；n表示均值为0、方差为σ2的高斯白噪声，n=[n1,n2,···,nN]T；C表示海杂波在均匀线性阵列N个阵元的输出数据矢量，C=A1s1，A1=[a(ϕ1),a(ϕ2),···,a(ϕP)]为海杂波的阵列流型，s1=[s1,s2,···,sP]T为 海杂波的复振幅；T表示目标在均匀线性阵列的N个阵元的输出数据矢量，T=A2s2，A2=[a(ϕP+1),(ϕP+2),···,a(ϕK)]为目标的阵列流型，s2=[sP+1,sP+2,···,sK]T为目标的复振幅.

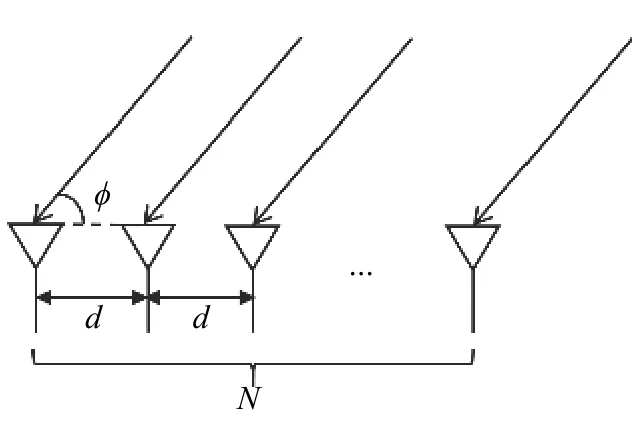
图2 均匀线性阵列Fig. 2 Uniform linear array

2.2 空域子空间估计与投影

出数据矢量可记为x，假设各信号源方位不同，其协方差矩阵为

对于RD谱中的一个谱点，阵列接收该信号的输

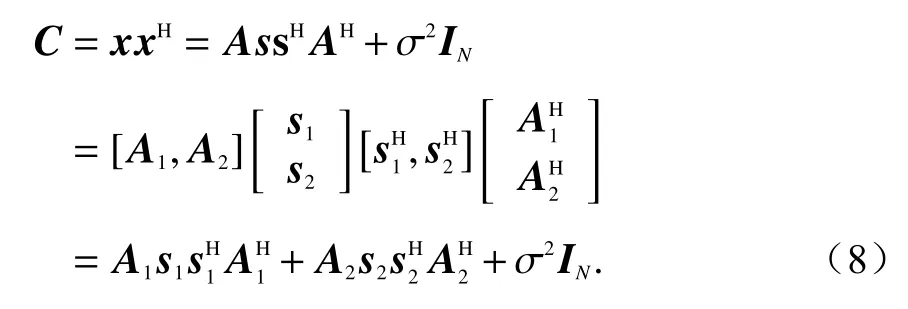
式中：A1和A2是相互正交的满秩矩阵；IN表示N维的单位矩阵.

为了估计空域的海杂波子空间和噪声子空间，对阵列接收信号的协方差矩阵C进行SVD运算：

式中：U代表左奇异矩阵；S代表由奇异值构成的对角阵；V代表右奇异矩阵. 由于海杂波的强度远大于噪声强度，因此根据奇异值的大小进行子空间的划分，大奇异值对应的矢量构成的子空间为海杂波子空间U1，小奇异值对应的矢量构成的子空间为噪声子空间U2，由于海杂波与目标在不同方位，U1和U2是正交的. 海杂波子空间的投影矩阵为U1U1H，噪声子空间的投影矩阵为将接收的回波信号x向U1空间进行投影，得到投影分量为

进而得到与海杂波子空间正交的子空间内的投影向量为

由于噪声子空间与海杂波子空间正交，根据矢量运算法则，经过子空间投影后，海杂波得到了抑制.

在实际运用中，由于目标回波信号与海杂波信号混杂在一起，无法从接收的回波数据中准确估计出杂波子空间. 因此在估计子空间时，利用海杂波在相近的距离元之间具有较强的相关性[17]，可以选择感兴趣谱点前后邻近的距离元对应谱点作为参考单元，来估计杂波子空间.

2.3 算法步骤

基于SVD的空域海杂波抑制的基本步骤如下.

1)对雷达接收机的每个天线单元接收的数据进行两次FFT得到RD谱，并选择感兴趣谱点作为待处理单元.

2)选择待处理单元前后邻近的谱点作为参考单元，对参考单元的数据进行短时傅里叶变换，并计算参考单元阵列输出数据矢量xf的协方差矩阵C.

3)对参考单元的协方差矩阵C进行SVD，并根据奇异值的大小，将空间化分为杂波子空间U1和目标与噪声子空间U2.

4)利用式(10)和(11)，将待处理单元阵列输出矢量x向U1空间进行投影，并从阵列输出矢量x中减去其在U1空间的投影分量x′，从而达到抑制海杂波的目的.

算法流程图如图3所示.

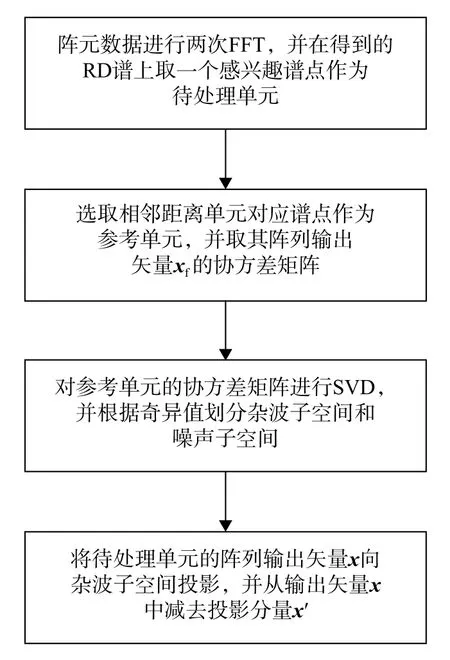
图3 算法流程图Fig. 3 Flowchart of the algorithm

3 理论仿真实验和基于实测数据的仿真实验的处理结果与分析

3.1 理论仿真实验处理结果与分析

利用仿真实验，将空域SVD算法对海杂波的抑制性能与现有的空域海杂波抑制算法进行对比. 在仿真海杂波时，设置载频为13.15 MHz，脉冲重复周期为0.5 s，积累周期数目为600，Bragg峰的多普勒频率为fB=±0.37 Hz，加入的噪声为高斯白噪声，设置海流的速度为0.5 m/s，正的一阶谱区的多普勒频率为[0.32,0.41]. 接收天线为八元天线阵，近似线性. 加入三个速度分别为4 m/s、4.5 m/s和−4 m/s的目标，对应的多普勒频率为0.35 Hz、0.39 Hz和−0.35 Hz，目标距离雷达站均为50 km，相对于雷达站的方位分别是北偏东65°、北偏东35°、北偏东10°，初始的信杂噪比(signal to clutter plus noise ratio, SCNR)为−8 dB、−15 dB和−10 dB，仿真得到的第一个天线单元的10号距离元的多普勒谱如图4所示. 可以看出，由于海流的存在，海洋回波的一阶谱发生了展宽，在[0.32, 0.41] Hz和[−0.41, −0.32] Hz两个频率区域内，回波信号强度较大，对应的正是展宽的一阶谱区. 由于仿真的目标回波强度低于海杂波，目标被海杂波淹没，箭头所指处仅是目标所对应的多普勒频率. 要想检测被淹没在一阶谱区的目标，需要对海杂波进行抑制.

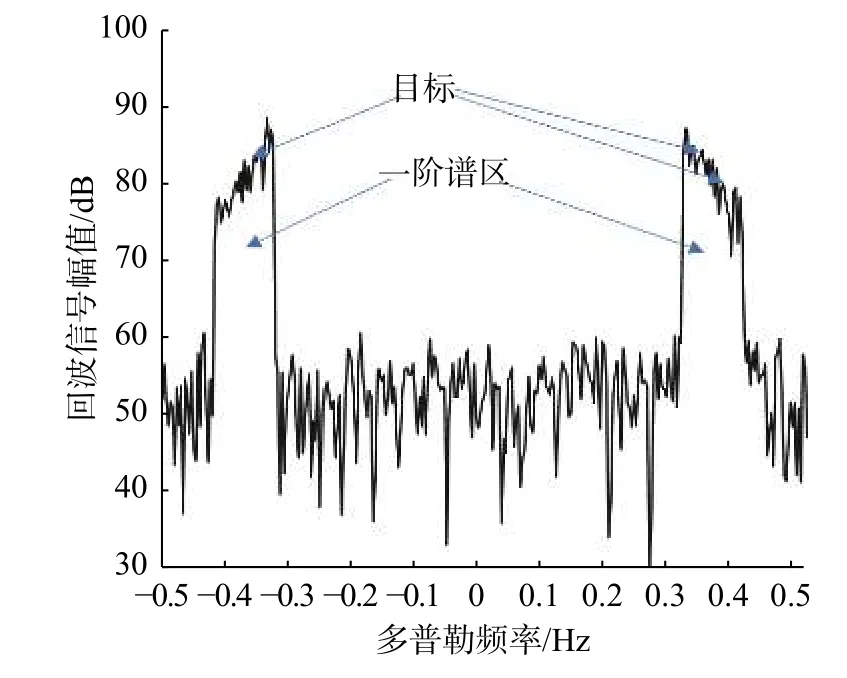
图4 海杂波抑制前的多普勒谱(仿真)Fig. 4 Doppler spectrum without sea clutter suppression (simulation)

图5给出了利用空域SVD算法、HOSVD算法和OP算法三种方法对海杂波进行抑制后的多普勒谱. 利用空域SVD算法处理数据时，由于实测实验中目标回波信号的旁瓣会泄漏到相邻距离元，因此在实际估计海杂波子空间时参考距离单元与感兴趣的距离单元中间间隔一个距离单元. 对一阶谱内的每一个谱点的阵列向量x减去其在海杂波子空间的投影，从而实现在空间维对海杂波的抑制. HOSVD算法则是利用一阶谱内多普勒维、距离维和方位维的三维数据构造三阶张量，通过HOSVD来抑制海杂波. OP算法是在已知海杂波方位情况下计算其阵列流型，并对一阶谱内的每一个谱点的阵列向量通过OP来抑制海杂波.

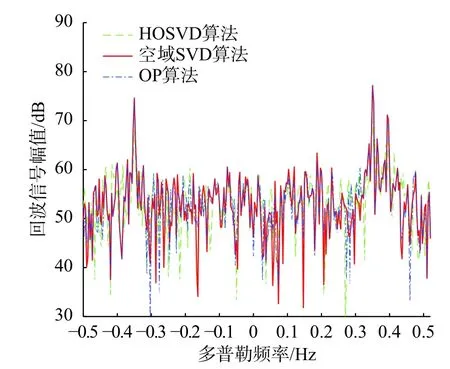
图5 抑制海杂波后的多普勒谱(仿真)Fig. 5 Doppler spectrum with sea clutter suppression(simulation)

从图5可以看出，在仿真实验中，三种算法均能抑制海杂波，使目标凸显出来，提高了SCNR，有利于一阶谱内目标的检测. 在海杂波方位已知的情况下，OP算法与空域SVD算法在海杂波抑制方面性能几乎是相同的，而且输出的SCNR比HOSVD算法至少提高了5 dB，使目标更加突出. 主要是由于空域海杂波抑制算法进行SVD的维数较低，RD谱上一个谱点对应的方位维信源个数较少，容易准确估计出海杂波子空间，对海杂波的抑制效果更好. OP算法预先已知海杂波方位，可以计算出其阵列流型和海杂波子空间，因此这两种算法通过投影消除海杂波均能有比较好的效果，而且对目标的影响较小. 而HOSVD算法对空间维、距离维和多普勒维进行了联合处理，SVD算法得到的奇异值个数较多，难以利用奇异值的大小进行子空间的准确划分，存在海杂波子空间向目标子空间的泄露问题，在消除海杂波的同时，也会造成目标能量被削弱.

为了验证算法的有效性，做了100次蒙特卡洛实验，图6为利用三种算法抑制海杂波之后的输出SCNR. 可以看出，空域SVD算法和OP算法输出的SCNR平均高于HOSVD算法约7 dB，而且具有较好的稳定性，说明在抑制海杂波方面，空域海杂波抑制算法具有较好的性能.

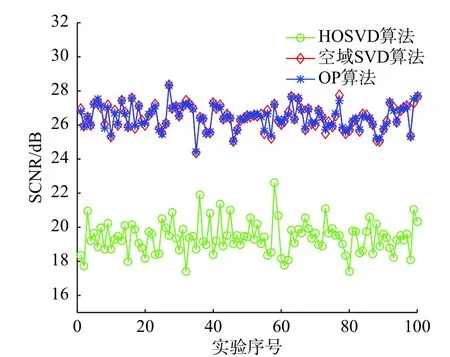
图6 抑制海杂波之后的输出SCNR(仿真)Fig. 6 Output SCNR with sea clutter suppression (simulation)

3.2 基于实测数据的仿真结果与分析

通过基于实测数据的仿真结果来对比分析HOSVD算法、OP算法和空域SVD算法对海杂波的抑制性能. 实验采用的是2016年12月26日东山站单站发射、单站接收的实验数据，雷达站接收天线共有八个单元，且近似成线性排列，雷达的工作频率为13.15 MHz，脉冲重复周期为0.5 s，Bragg峰的多普勒频率为fB=±0.37Hz，脉冲积累周期数为600，积累时间为5 min，距离分辨率为5 km. 实验过程中，在实测数据中加入了三个仿真目标，目标均在距离雷达站50 km处，相对于雷达站的方位分别是北偏东30°、北偏东60°、北偏东45°，速度分别为正北5 m/s、正西5 m/s、正北6 m/s，对应的多普勒频率为−0.38 Hz、0.38 Hz、−0.36 Hz，初始的SCNR均为−5 dB，目标被完全淹没，加入仿真目标后的10号距离元的多普勒谱如图7所示. 把海流流速为± 0.5 m/s对应的多普勒区域当作是一阶谱区，对应的多普勒频率区间分别为[0.32，0.41] Hz和[−0.41，−0.32] Hz.

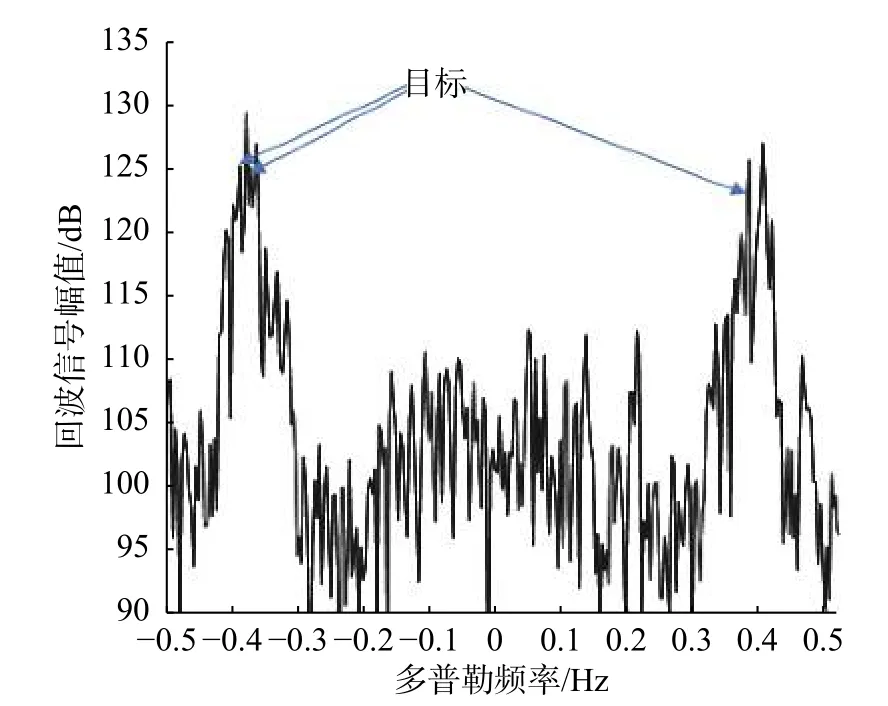
图7 加入仿真目标后的多普勒谱(实测)Fig. 7 Doppler spectrum with simulation target (measured)

分别利用HOSVD算法、OP算法和空域SVD算法对数据进行处理. 在运用空域SVD算法抑制海杂波时，参考单元与感兴趣距离单元之间间隔一个距离元，经过SVD后，将前5个大奇异值对应的子空间设为海杂波对应的子空间；HOSVD算法中三阶张量的构造依然是利用前20个距离元、一阶谱区的多普勒元与所有阵列单元的数据；对于实测数据，无法预先知道海杂波的方位，通过MUSIC算法为OP算法提供海杂波的估计方位，进而得到海杂波的子空间. 目标所在的10号距离单元利用三种算法对海杂波进行抑制后的多普勒谱如图8所示.

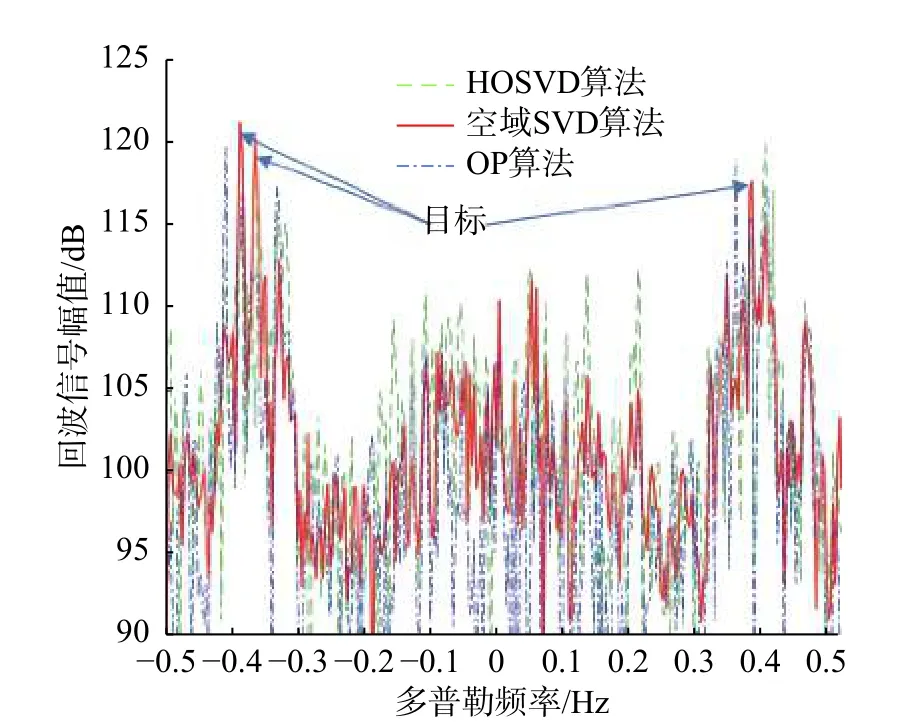
图8 抑制海杂波之后的多普勒谱(实测)Fig. 8 Doppler spectrum with sea clutter suppression(measured)

从图8可以看出，HOSVD算法、OP算法和空域SVD算法都能抑制较强的海杂波分量，在目标处形成一个尖峰，然而空域SVD算法抑制海杂波后输出的SCNR比HOSVD算法至少高4 dB，OP算法输出的SCNR介于两者之间，因此空域SVD算法在图8中形成的尖峰比较明显. 产生上述现象的原因是实测数据的一阶谱区的海洋回波分量比较复杂，根据经验划分的海杂波子空间与噪声子空间不准确，海杂波子空间向噪声子空间的扩散造成海杂波不能被有效消除，旁瓣较高，子空间划分不准确，对HOSVD算法海杂波的抑制性能影响较大. 而空域SVD算法进行SVD时，奇异值数目较少，比较容易进行子空间划分，且子空间投影算法利用两个相距较近的距离元的空域信息，海杂波的相关性比较强，通过投影法海杂波消除得更充分，对目标影响较小. OP算法要求预先知道的海杂波子空间信息在实测中无法得到，通过MUSIC算法估计海杂波的方位，进而获取子空间，使得误差较大，因此实测中对于海杂波的抑制效果OP算法比空域SVD算法稳定性差. 在实测中三种算法的性能都比仿真结果差，可能是实测中海杂波子空间和噪声子空间不完全正交，海杂波不能完全被消除造成的.

为了验证算法的有效性，利用三种算法进行了基于24场2个小时实测数据的仿真实验，图9为利用三种算法抑制海杂波之后的输出SCNR.

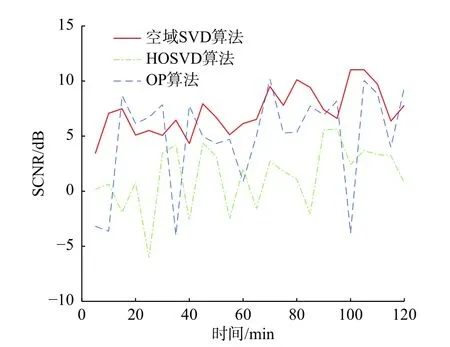
图9 抑制海杂波之后的输出SCNR(实测)Fig. 9 Output SCNR with sea clutter suppression (measured)

从图9可以看出：空域SVD算法的输出SCNR比HOSVD高约5 dB，OP算法的输出SCNR介于两者之间；但OP算法输出SCNR波动比较剧烈，因为通过MUSIC算法估计海杂波方位，进而获取海杂波对应的阵列流型和子空间会存在较大误差，进而影响OP算法的性能. 这三种算法的输出SCNR随着时间变化都会波动，在抑制海杂波时都有一定效果，但是不能完全抑制海杂波，目标周围的杂波残余分量会变化，最终造成输出SCNR的起伏. 图10给出了这2个小时内海流方位与目标方位之间的角度差.可以看出，虽然目标的方位不变，但是海流的方向会发生变化，海流与目标之间的方位差会随时间变化.由于空域SVD算法是在空域对海杂波进行抑制，当目标与海杂波的来波方向相同或相近时，目标存在被误消的可能，也会造成输出SCNR的起伏.

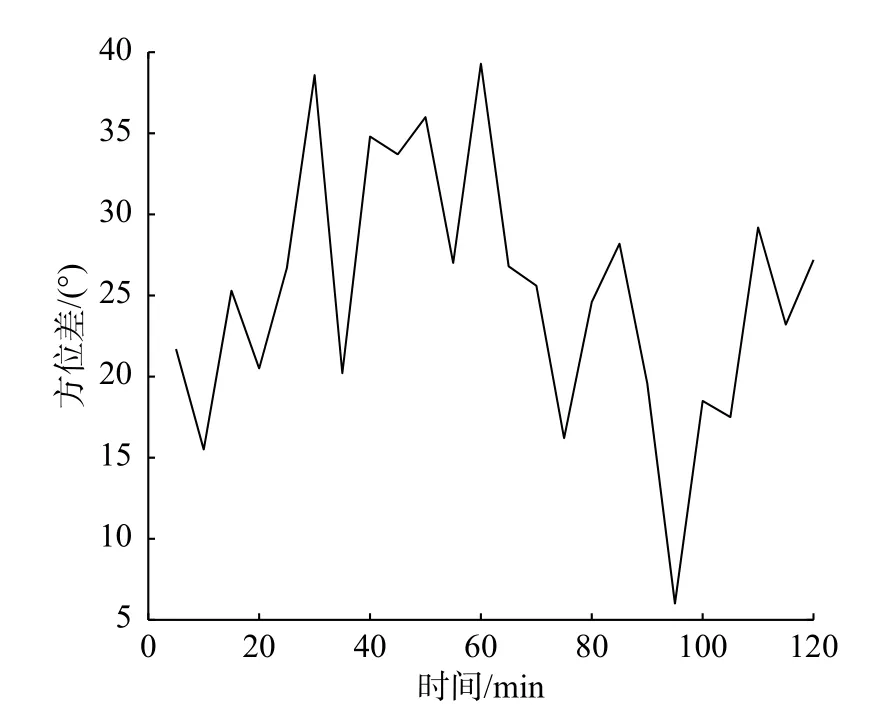
图10 海流和目标方位之间的差值(实测)Fig. 10 Difference of direction between current and target(measured)

4 结 论

本文在SVD的基础上提出了空域SVD算法，用于一阶谱区海杂波的抑制，进而实现一阶谱中目标的检测. 对算法进行了理论分析和推导，并利用仿真与实测数据验证了算法的有效性. 理论仿真和基于实测数据的海杂波抑制结果均表明，与HOSVD算法、OP算法相比，空域SVD算法在未能预先知道海杂波的子空间的情况下，能够比较准确地估计海杂波子空间，产生比较好的海杂波抑制效果；该算法利用海杂波在距离上的相关性，通过在空间域子空间投影抑制海杂波，不受目标多普勒频率与Bragg频率差值大小的影响；在空间域进行SVD，奇异值数目较少，容易划分杂波子空间与噪声子空间，对海杂波有比较好的抑制效果. 但是该算法的性能受到海洋回波在距离上相关性的影响，应用有一定的局限，而且只能将海杂波分量消弱，并不能完全消去海杂波；当目标与海杂波处于相同或相近方位时，存在目标被误消的情况.