AES相关故障注入攻击

王省欣，胡 伟，谭 静，朱嘉诚，唐时博

(西北工业大学 网络空间安全学院，陕西 西安 710072)

密码算法实现在执行过程中通常会泄漏一些算法功能规范之外的信息，如加密时间、能量消耗、电磁辐射和出错情况等。根据这些信息进行数学分析来获取秘密信息，即侧信道分析[1-2]。如通过对非对称加密算法(Rivest-Shamir-Adleman，RSA)的时序攻击来获取密钥[3]。常见的侧信道分析方法包括时序分析、能量分析、电磁分析和故障分析等[4]。其中，故障注入攻击通过向密码算法实现执行过程中引入故障，并通过观测故障效应和数学分析来恢复算法密钥。故障分析是一种针对对称和非对称加密算法非常有效的密码分析技术[5-7]。

当高级加密标准(Advanced Encryption Standard，AES)被普遍采用后，研究者提出了大量针对AES的故障注入攻击方法[8-15]。PARK等在字节变换中注入故障，分析S盒输入和S盒输出之间的关系，破解密钥[8]。一些研究通过向AES加密变换注入单字节故障来破解密钥[9-11]，也有学者提出了针对密钥扩展的故障注入攻击方法[12]。GHALATY等提出利用差分故障强度分析，通过平均7次对AES的故障注入攻击，重建完整的128位加密密钥[13]。通过引发2字节故障，ZHANG等利用差分故障分析方法破解密钥[14]。POGUE等提出用增量故障分析的方法对不同密钥长度的AES加密算法进行破解[15]。然而，上述故障注入攻击方法大多对故障注入的位置、时机和数量有严格要求，且密钥恢复过程需要复杂的数学分析，或需要大量时间来训练故障攻击模板。

笔者提出一种针对AES的相关故障注入攻击方法，利用AES故障效应传播中的相关关系恢复密钥。该攻击方法对故障注入位置和数量要求更为灵活，在不同密钥长度AES算法实现倒数第3轮(Nr- 2)列混合变换前至S盒变换之间任意位置注入随机故障后，分析最后一轮S盒输入的故障效应相关关系，即可恢复最后一轮的轮密钥；在192位和256位AES算法实现倒数第4轮(Nr- 3)列混合变换前至S盒变换之间任意位置注入随机故障后可恢复倒数第2轮(Nr- 1)列的轮密钥。该方法的密钥搜索复杂度为216，只需2个正确-错误密文对或同一明文下的4条错误密文即可恢复128位AES初始密钥；只需4个正确-错误密文对或同一明文下的8条错误密文即可恢复192和256位AES初始密钥。

1 背 景

1.1 AES算法结构

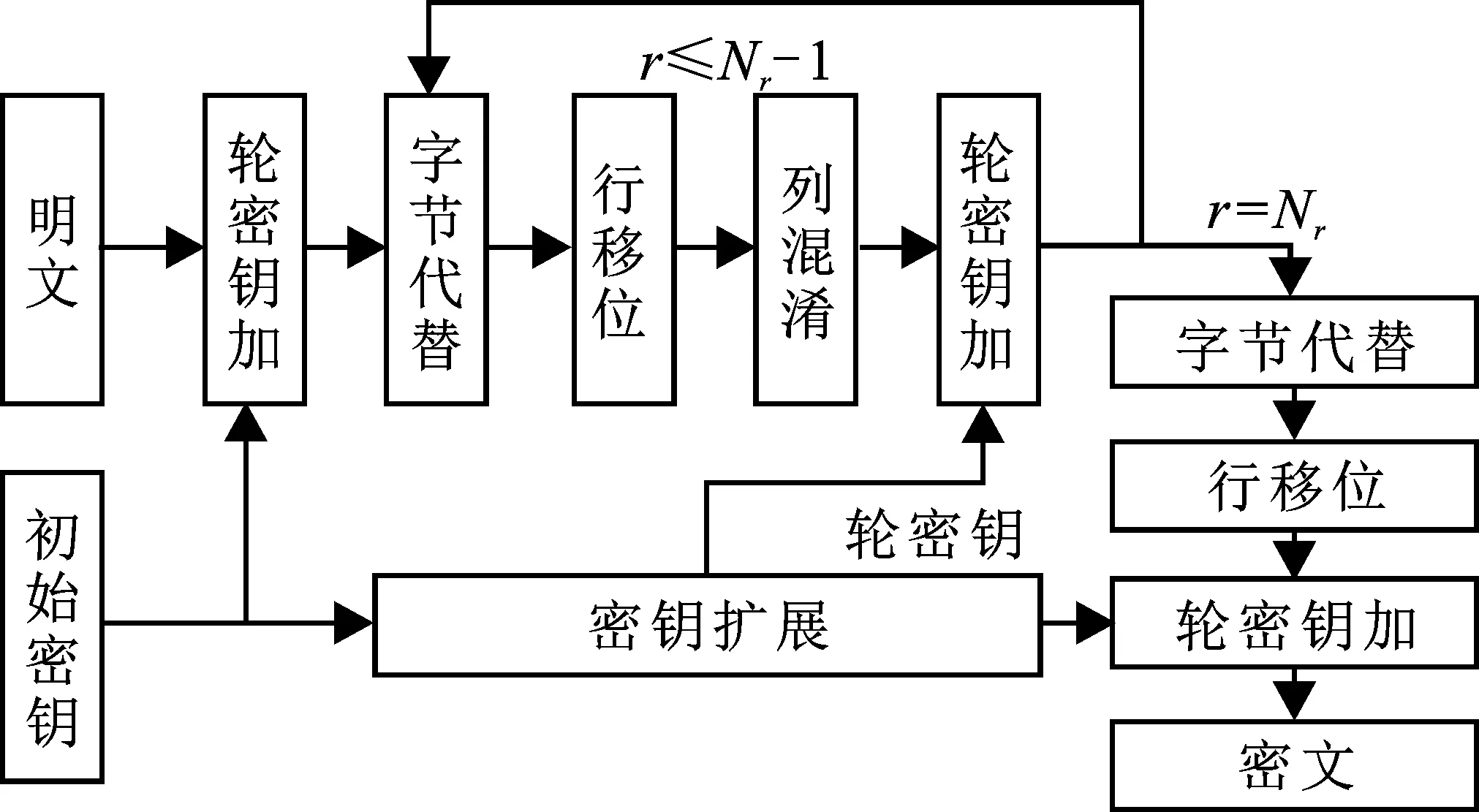
图1 AES加密算法流程示意图

AES是一种分组密码算法，数据分组长度为128 bit，密钥支持128 bit、192 bit和256 bit 3种长度。图1为AES算法结构，其中，r表示加密轮数，Nr(Nr= 10，12，14)表示加密迭代的总轮数。

AES是一种典型的迭代算法结构，由轮函数和密钥扩展构成。轮函数包括4种基本变换，字节代替(S-Box，SB)，行移位(ShiftRows，SR)，列混淆(MixColumns，MC)和轮密钥加(AddRoundKey，ARK)。值得注意的是，AES加密算法中最后一轮加密不包含列混淆变换。

字节代替是AES中的非线性部件，各字节通过8位的S盒进行转换，其每位输入对多位输出存在影响。行移位是一种线性移位操作，不改变中间状态的值，只是对128 bit的中间状态按算法定义的规则以字节为单位进行移位。列混淆会通过状态字节之间的线性变换将字节代替的非线性混淆效应在状态字节之间进行扩散。轮密钥加变换通过与轮密钥的线性异或操作来引入混淆。

1.2 AES故障效应传播

AES的数据分组和加密中间状态通常表示为4×4的状态字节矩阵S，矩阵中每一个元素(S0～S15)为1个字节。如图2，状态矩阵中某字节发生故障，则故障会通过轮变换传播扩散，增大故障的影响范围。

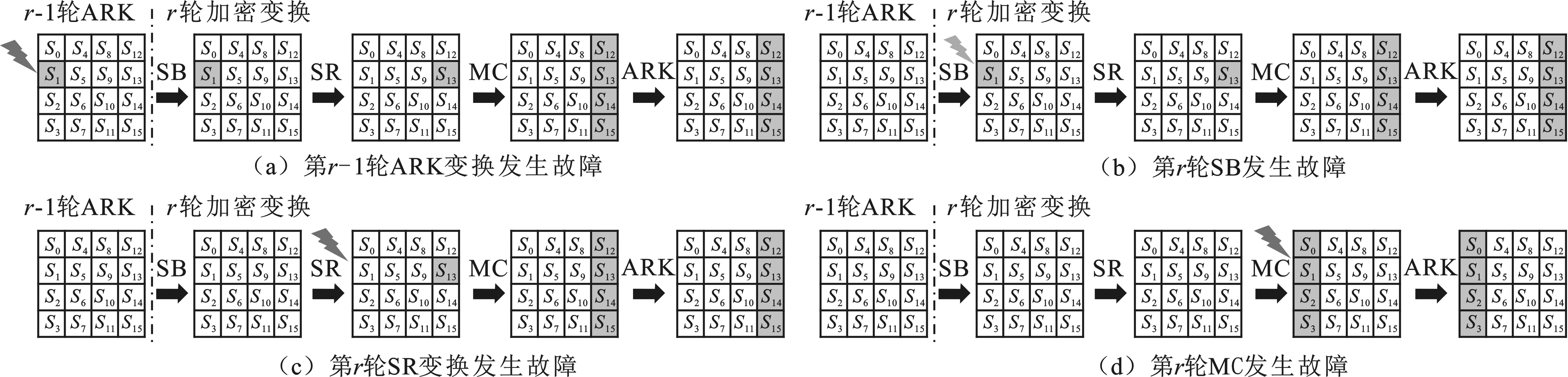
图2 第r轮内单字节故障传播示意图

图2以轮内各变换输入状态矩阵中字节S1发生故障为例，带颜色表示故障字节，展示了轮内变换单字节故障传播效应。在不同状态字节注入故障，传播过程与此相似，但最后影响的状态字节位置有所不同。

字节代替是以字节为单位的变换，故障只影响相应字节代替中相应的输出字节。由于字节代替为非线性部件，因此，无法确定输出的故障位置和数量。行移位变换为线性移位，不改变故障类型，仅是故障字节在状态矩阵中的位置发生变化。列混淆变换虽为线性变换，但会通过状态字节的线性变换将单字节的故障效应扩散到一列的4个状态字节，且该4个状态字节的故障效应满足线性相关关系。轮密钥加变换将状态字与轮密钥进行线性异或，不会对状态字的故障类型造成影响，因此在r-1轮轮密钥加注入故障和在r轮字节代替注入故障效果一致，可将在r-1轮轮密钥加攻击和在第r轮字节代替注入故障归为同一类攻击。由图2可知，在每轮列混淆变换之前注入单字节故障，经轮内变换后故障都传播到4个状态字节。

由上述分析可知，列混淆变换的故障传播效应相对复杂，列混淆变换的线性特性会使4个输出字节之间的故障效应存在线性相关关系。在第r+1轮加密中，第r轮中每个字节的故障效应继续传播至4个字节，经过该轮列混淆变换后，每个错误字节各自影响该列的4个字节，因此，4个状态字节的故障进一步传播和扩散到16个状态字节，但每列4个字节的故障效应仍然具有良好的线性相关关系。利用这种故障效应相关关系，提出了一种针对AES的简单相关故障注入攻击方法。

2 故障注入攻击模型

假设攻击者拥有运行的加密设备，但不知道加密密钥。攻击者能够为加密设备施加明文，并观测加密结果。集成电路正常工作依赖于稳定的时钟和电压信号，因此攻击者可通过调节电压、改变时钟频率，或向电源和时钟信号中注入毛刺来进行故障注入攻击。另外，攻击者也可用激光照射或高能粒子扰乱密码设备的正常运行，实现故障注入攻击。

假设攻击者掌握了加密设备上AES算法实现的细节信息，能够准确地在第Nr-1至Nr-3轮的任一运算注入单字节的随机故障。攻击者不知道故障注入的具体位置或者故障类型及数量，并且任意两次注入的故障都可能是不同的(随机故障)。

如图3所示，对虚框中的运算实施故障注入攻击，观测注入故障后的加密结果。攻击者可利用获得的错误加密结果与对应的正确加密结果进行对比相关性分析，从而恢复算法的加密密钥。

图3 故障注入位置示意图

文中提出的故障注入攻击方法利用了AES加密算法的结构特征和故障传播效应内在的线性相关关系，与现有故障注入攻击方法相比，无需复杂的数学推导和故障攻击模型训练过程，且对故障类型要求更为灵活，可以为随机故障。

首先以128位AES为例，介绍相关故障注入攻击方法，然后讨论将该攻击手段扩展至192和256位AES的方法。

3 相关故障注入攻击

基于1.2节讨论的AES故障效应传播特征，文章提出了一种针对AES实现的相关故障注入分析方法。对于128位AES实现，该方法在AES算法第Nr-1和第Nr-2轮任意位置注入随机故障后，分析最后一轮字节代替输入的故障效应相关关系即可恢复最后一轮的轮密钥。

3.1 故障效应相关性分析

以在S0中注入故障为例(如图4所示)，不同颜色代表无关的故障类型，相同颜色代表线性相关的故障类型。由图可知，在第Nr-1轮实施攻击，故障传播到4字节，在第Nr-2轮实施攻击，故障传播至16字节，但每列4字节的故障效应存在线性相关关系，区别在于第Nr-1轮注入故障后只经历1次列混淆变换。

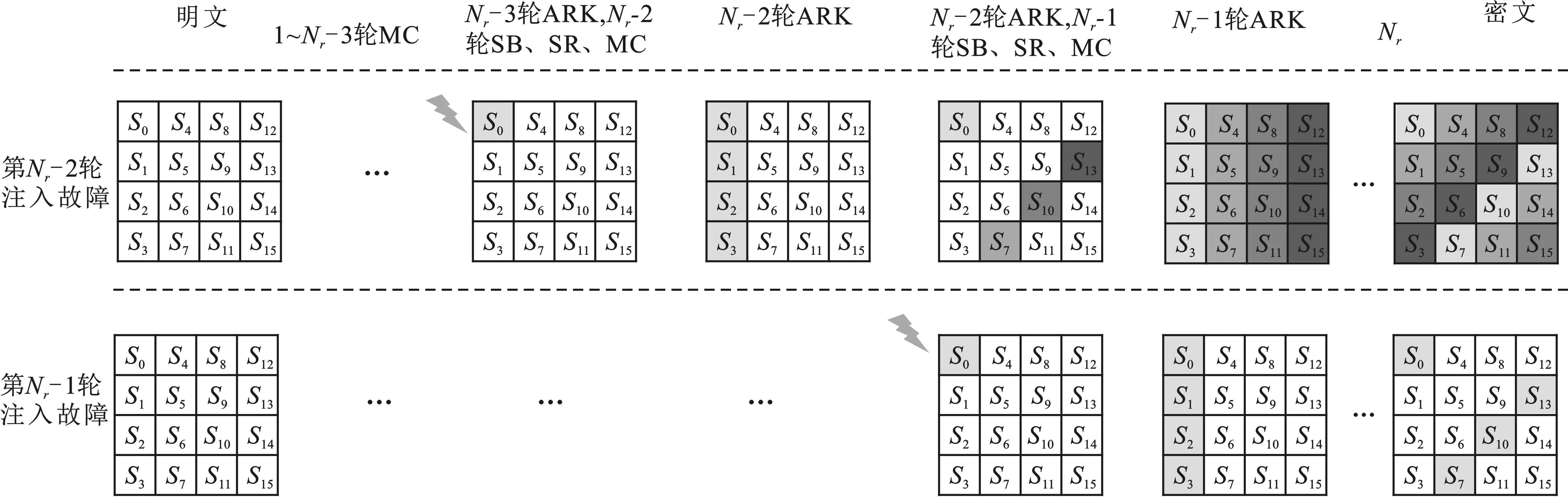
图4 第Nr-2轮和第Nr-1轮故障传播过程示意图

假设在第Nr-2轮状态矩阵的S0注入的随机故障为ε，经过该轮的字节代替后，错误信息变为ε0。由于故障注入位置为S0，此时行移位对故障传播无影响。如式(1)所示，表示该轮列混淆变换后故障传播的结果，其中，ε0，ε1和ε2代表不同故障。

(1)

状态矩阵S经过第Nr-2轮的字节代替和行移位变换后，4个字节的故障发生变化且相互独立，分别用α0，β0，γ0，δ0表示。如式(2)所示，列混淆变换后故障扩到全部16个字节，但各列4个字节之间故障的位置和数量仍存在线性相关关系。

(2)

根据AES加密算法的特点，最后一轮不存在列混淆变换，因此，可通过假设最后一轮的轮密钥，逆向构造最后一轮字节代替输入(即第Nr-1轮输出)的故障效应，并检验状态矩阵每列4个字节的故障效应的线性相关关系来确定正确密钥。

(3)

(4)

(5)

然后，当d1最高比特位未发生故障时，通过测试式(6)所示的线性关系来恢复d2对应的密钥字节，否则测试式(7)。

d2=d1或d2=(d1≪1) 。

(6)

d2=(d1≪1)⊕0×1B 。

(7)

最后，测试式(8)来恢复d3对应的密钥。

d1=d2⊕d3。

(8)

如图5所示，在第Nr-1和第Nr-2轮状态字节S0随机注入单字节故障，正确-错误密文对或2条错误密文各自在第Nr-1轮的加密结果通过进行异或运算获取故障信息Di。图中以对虚框中内容进行异或运算为例，获得错误信息D0。

图5 故障效应传播的错误信息示意图

3.2 密钥搜索算法

由3.1节可知，仅需分析第Nr-1轮加密结果故障效应的相关关系，即可破解Nr轮加密密钥。由于Nr轮加密行移位变换改变了输入状态矩阵中故障字节的位置，如表1所示，可将AES的加密结果分为4组目标字节Bi(0≤i≤3)。通过分析对应目标字节Bi的正误密文，获取第i列密钥信息。

表1 目标字节Bi的分组

攻击者能够通过观察密文中故障字节的数量和位置，并根据表1、式(3)～(8)来恢复密钥。所采用的密钥恢复算法如下。

算法1密钥恢复算法。

输入：密文对(C，C′)。

输出：最后一轮轮密钥Kr。

① 根据C和C′选择字节组合Sw，Sx，Sy，Sz

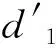
③ forSi，Sj字节组合对应的Nr轮轮密钥字节ki，kjin 0 ：216DO

④Si= S-Box-1(Ci⊕ki)

⑤Sj= S-Box-1(Cj⊕kj)

⑥Si′= S-Box-1(Ci′⊕ki)

⑦Sj′= S-Box-1(Cj′⊕kj)

⑧εi=Si⊕Si′

⑨εj=Sj⊕Sj′

⑩ IFεi和εj满足式(3)～(5) THEN

该算法通过相关性分析方法，恢复Nr轮加密密钥。先在密文对中选出目标字节Bi，猜测Bi对应的密钥字节，然后对Bi执行逆轮密钥加和逆字节代替变换，恢复2条密文对应的第Nr-1轮加密结果，对比可得故障信息Di。若密钥字节猜测正确，则Di的对应字节满足式(3)～(8)中的相关关系，否则无显著相关关系。

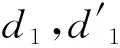
3.3 192位和256位AES攻击方法

不同密钥长度的AES最后一轮加密变换相同，因此可通过算法1方法对192位和256位AES进行攻击，获得轮密钥Kr。然而，仅根据最后一轮128位的轮密钥不足以恢复192和256位AES的原始加密密钥，需再恢复Nr-1轮的64位或者128位轮密钥之后才能完全实现192和256位AES密钥的破解。

为了恢复第Nr-1轮的轮密钥，进一步向第Nr-3轮的列混淆变换之前注入随机故障，然后，利用第Nr-1轮的字节代替输入的故障效应相关关系，采用类似的相关故障分析方法来恢复密钥。如图6所示，利用已破解的轮密钥Kr，重构第Nr-1轮的中间加密结果。对该中间加密结果进行逆列混淆变换，通过算法1每次分析破解4字节加密密钥，然后对破解的密钥再进行对应的列混淆变换即可恢复第Nr-1轮的密钥字节。

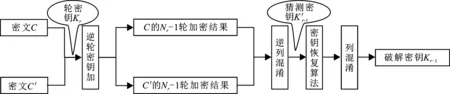
图6 恢复第Nr-1轮密钥

4 实验结果

4.1 AES相关故障注入攻击实验

由3.1和3.2节可知，可在第r-1轮和第r-2轮进行故障注入攻击，获取第r轮加密密钥。第r-1轮一次攻击只可破解32位第r轮密钥，需在状态矩阵各列进行一次攻击，才可破解128位轮密钥信息。而第r-2 轮一次攻击即可破解128位第r轮密钥。表2显示了不同AES加密算法故障注入位置与可恢复密钥数量之间的关系。

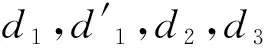
4.2 故障注入攻击结果

4.2.1 128位AES故障注入攻击结果

在第8轮和第9轮加密变换输入的第0至15字节注入单字节的随机故障破解第10轮密钥，执行单字节随机故障注入攻击960次，故障注入攻击分析结果如表3所示。当分析1个密文对时，可选密钥较多，当有2个密文对时，仅少数情况有多于1个密钥猜测，备选密钥数量已处于可测试验证范围内。

4.2.2 192位AES故障注入攻击结果

与128位AES故障攻击类似，在192位AES算法的第10轮和第11轮进行攻击，破解第12轮加密密钥。利用破解的第12轮加密密钥，在第9轮和第10轮进行第二次故障注入攻击，破解64位的第11轮加密密钥，执行单字节随机故障注入攻击1 280次，故障注入攻击分析结果如表4所示。分析1个密文对时，最大备选密钥数量和最小备选密钥数量差异较大，分析2个密文对时，备选密钥已处于可测试验证范围内。

表4 192位AES故障注入攻击结果

4.2.3 256位AES故障注入攻击结果

256位AES也需进行两次故障注入攻击破解第14轮和第13轮密钥。在第12轮和第13轮进行攻击破解第14轮密钥后，再通过在第11轮和第12轮注入故障，分析第13轮密文的相关关系，破解第13轮加密密钥，执行单字节随机故障注入攻击1 280次，故障注入攻击分析结果如表5所示。与192位和128位攻击结果类似，当有2个密文对时，仅少数情况有多于1个密钥猜测，能够通过测试验证恢复全部密钥。

表5 256位AES故障注入攻击结果

利用文章所提出的攻击分析方法，可通过匹配式(3)～(8)所示的4种相关关系判断猜测密钥的准确性，不需大量的数学推导，通过有限域GF(28)的逆运算即可恢复密钥。以上实验结果验证了利用单字节随机故障实施相关故障分析来恢复不同长度AES算法密钥方法的有效性。只需2个正确-错误密文对或同一明文下的4条错误密文即可恢复128位AES初始密钥；需4个正确-错误密文对或同一明文下的8条错误密文即可恢复192和256位AES初始密钥。

5 结束语

笔者利用AES密码算法的结构特征和故障传播效应的线性相关关系，提出一种针对AES的简单相关故障注入攻击方法。与其他故障注入攻击方法相比，该方法无需复杂数学推导，注入故障的位置和数量要求灵活，也适用于唯密文攻击。