光干涉绝对重力仪测量A 类不确定度优化
2021-09-01李春剑吴书清粟多武冯金扬王启宇
李春剑,吴书清,粟多武,冯金扬,王启宇
(中国计量科学研究院 时间频率计量科学所,北京 100029)
1 引 言
重力加速度g是一个随着空间和时间不断变化的物理量,其量值在地球物理学[1]、测地学[2-3]及计量学[4-5]等领域是一个十分重要的地理参数[6-7]。在地球物理学、测地学领域,重力加速度g值是地球内部密度结构、地球表层密度变化、山脉边缘动态补偿等研究非常重要的地理参数[8-9]。在计量学领域,重力加速度g值会影响“测力”及其相关的力值标准,如压力、扭矩等,同时精确的重力加速度g值还会影响国际单位制中7 个基本单位之一——质量单位“千克”的重新定义,即功率天平和能量天平的建立。上述领域对重力加速度g值的要求为10-5~10-9量级。然而,由于地壳板块的运动[2],重力加速度g值每年的变化量为1 微加(1 μGal=10-8m/s2)或是几微加,若想观测到该量级的变化就需要借助精度在对应数量级的仪器设备。高精度的相对重力仪可以实现微加级相对重力值的测量,然而相对重力仪存在着定期的校准、测量范围受限、长期漂移等问题,高精度的绝对重力仪即可解决这些问题[6,8]。
绝对重力仪根据测量方法不同,分为单摆式绝对重力仪、光干涉绝对重力仪和原子干涉绝对重力仪。其中,光干涉绝对重力仪和原子干涉绝对重力仪的精度较高,可达10-9量级。光干涉绝对重力仪为目前主流的绝对重力仪[10],具备自主研制能力的国家包括美国[2,11]、俄罗斯、意大利、波兰和中国。美国研制的FG5、A10 型绝对重力仪已商品化。法国研制的原子干涉绝对重力仪是第一台不同测量原理的绝对重力仪,并已参加了两次国际比对。我国多家单位在进行绝对重力仪的研制,包括光干涉绝对重力仪[12-14]和原子干涉绝对重力仪[15-17]。光干涉绝对重力仪的实现方式分为自由下落法和上抛下落法,均利用光学干涉仪对被测落体的轨迹进行监测[18-19],同时记录时间,通过位移-时间拟合得到重力加速度g值。位移和时间的测量精度直接影响重力加速度g值的测量精度。时间测量的测量精度由高精度铷钟来保证;被测落体相对于地球位移变化的测量精度受落体的偏摆、参考棱镜随地面振动大小的影响。利用机械结构精确定位可保证落体的偏摆在允许范围内,然而参考棱镜随地面振动是无法避免的,这会直接影响重力仪单次的测量数据。由于地面振动是随机的,可利用多次测量取平均消除地面振动对测量结果准确性的影响,然而大量实验,多次测量得到的结果的分散性比较大,也就是测量结果的A 类不确定度较大。针对上述问题,美国FG5 型绝对重力仪将参考棱镜放置于一个名为Super Spring[2]的长周期主动隔震台上,其隔振周期为60 s,能够有效地隔离地面振动给参考棱镜带来的影响。意大利IMGC-02型绝对重力仪[20-21]和俄罗斯ABG-VNIIM-1 使用零长弹簧被动隔振原理对参考棱镜进行隔振。清华大学研制的T 型绝对重力仪[12]采用主动隔振[22]的方法对参考棱镜进行隔振。
本文针对自制的NIM-3A 型绝对重力仪,使用测振补偿法进行隔振,测量重力加速度时将地面振动记录下来,数据处理时将其补偿到干涉仪监测的被测落体下落位移(落体相对于参考棱镜的位移)上。处理后的被测落体下落位移更加接近实际发生位移,这样有效减小了地面振动对测量结果的影响,提高了单次测量的准确性。
2 NIM-3A 型绝对重力仪
2.1 测量原理
在重力场中,由万有引力公式可推导出自由落体加速度公式如下[23]:

其中:s为自由落体的位移,G为万有引力常数,M为地球的质量。
考虑到重力梯度,且它为线性时,则有:
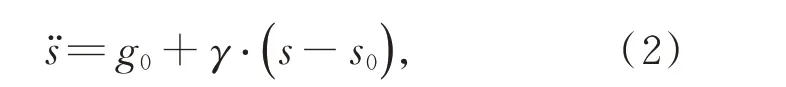
其中:g0和s0分别为t=0 时刻的初始重力加速度和初始位移,γ为重力梯度。
求解微分方程(2),得到:
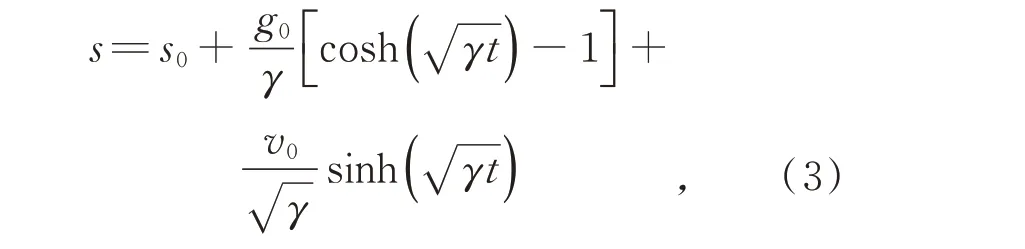
其中v0为t=0 时刻的初始速度。

若重力梯度γ已知,通过位移和时间进行二次项拟合即可得到重力加速度g值。
2.2 测量方法
NIM-3A 型绝对重力仪采用上述测量原理进行重力加速度测量。当被测落体在重力场中自由下落时,精确测量被测落体的下落位移和时间,进而拟合得到重力加速度g值。具体如下:利用激光干涉仪(迈克尔逊干涉仪)监测自由下落物体的轨迹[25],其光路见图1,激光光束从激光器中发出,通过分光镜分为两束,反射的一束为测量光束,透射的一束为参考光束;测量光束照射到置于真空腔内的被测落体(直角立体棱镜)上发生反射,经分光镜至参考棱镜,又经参考棱镜反射至分光镜,与参考光束汇合;当被测落体下落时,反射回来的测量光束和透射的参考光束发生干涉,产生干涉条纹;干涉条纹的个数对应被测落体的下落位移,同时记录下落的时间。通常采用多点测量,利用最小二乘拟合法得到重力加速度g值。
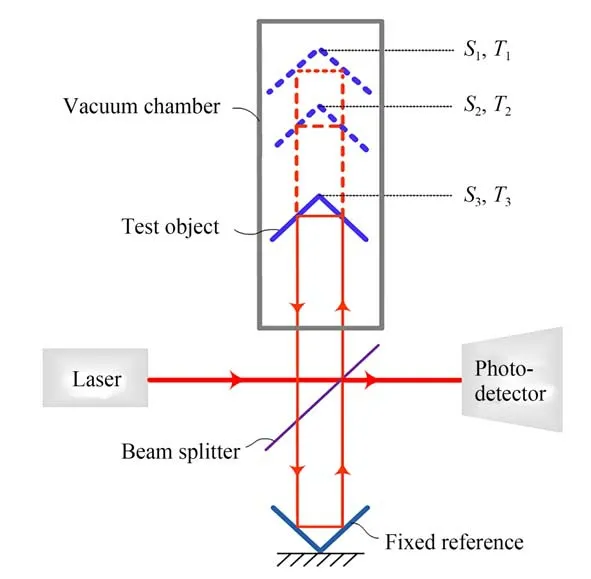
图1 光干涉绝对重力仪的光学系统Fig.1 Optical system of interferometric gravimeter
2.3 测量系统
测量装置包括真空系统、机械传动系统、光学系统、测振系统以及电气系统,如图2 所示。其中,真空系统为真空腔部分,被测落体置于其中进行自由落体运动,一般真空度小于1×10-4Pa。机械传动系统包括电机、过真空传动轴、钢带、传动导杆、托盘及被测落体。电机通过过真空传动轴与钢带相连,钢带带动托盘上下运动,托盘内有个与之分离的被测落体(直角立体棱镜)。当钢带带动托盘向下高速运动时(托盘加速度大于1g),被测落体实现自由下落。光学系统包括激光器、光学干涉仪(2.2 所述迈克尔逊干涉仪)和光电探测器,监测被测落体的下落轨迹,原理如图1 所示。测振系统包括拾振器(测振仪)和振动采集仪,用于监测并记录地面振动情况。电气系统包括上位机、电机传动控制器、干涉条纹和地面振动采集系统、铷钟(频率标准)以及激光控制器。
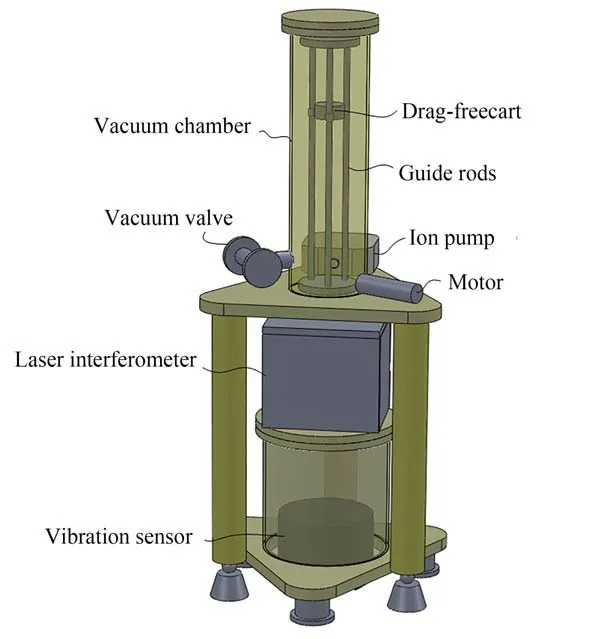
图2 NIM-3A 型绝对重力仪光机真空部分Fig.2 Mechanical vacuum system and laser interferometer of NIM-3A
NIM-3A 型绝对重力仪通过上位机控制整个装置。测量开始时,上位机向电机传动控制器发出“启动”指令,电机通过钢带带动托盘(落体置于托盘内)升至最高点,暂停几秒钟待被测落体稳定后,电机带动托盘加速下降(加速度大于1g),被测落体实现自由下落,干涉仪发生干涉。在被测落体下落的瞬间,上位机通知采集卡开始干涉条纹和地面振动信号的采集。当落体到达最低点后,暂停几秒钟,重复上升-下降的动作。在下一次下落之前,上位机计算得到本次下落的测量结果。当测量次数达到设定值后,上位机通知电机控制器“停止”电机运动,并计算全部下落的测量平均值、不确定和统计直方图等,测量结束。测量也可设置为特定时刻开始的循环测量。
3 地面振动的影响
光干涉绝对重力仪在高真空条件下精确测量被测落体在重力场中自由下落所经历的位移和时间,然后计算得到重力加速度。其中,位移测量利用迈克尔逊干涉仪实现。参考棱镜置于地面,干涉仪产生的干涉条纹对应被测落体相对于参考棱镜(地面)的位移变化。理想状态下,参考棱镜需相对于地球中心静止,然而地球表面除了大地脉动外还受其他振动源的干扰,因此,激光干涉法所测的位移变化与实际有些偏差,被测落体下落的位移测量也不准确,最终位移-时间拟合得到的重力加速度不准确。由于地面振动是随机的,可通过多次测量取平均的方法消除地面振动对测量结果准确度(被测量的测得值与其真值间的一直程度)[19]的影响。然而,这样需要进行大量的实验,并且多次测量结果的分散性比较大,A 类不确定度[26]也会比较大。
针对上述问题,本文提出振动补偿法来提高NIM-3A 型绝对重力仪的精度。
4 测振补偿法
4.1 测振补偿系统
NIM-3A 型绝对重力仪测量重力加速度时将地面振动(参考棱镜相对于地球中心的位移)记录下来,数据处理时将它补偿到干涉仪监测的对应位移(被测落体相对于参考棱镜的位移)上,得到被测落体自由下落的位移。
位移补偿示意图如图3 所示,激光干涉仪监测被测落体的位移为x,参考棱镜随地面振动的位移为y,均以竖直向下为正方向。补偿后得到被测落体相对于地球的位移为z=x-y,这样z相比于y将更加接近实际发生位移,有效地减小了地面振动对位移测量的影响。

图3 位移补偿示意图Fig.3 Schematic diagram of displacement compensation
高精度绝对重力仪进行测量的点位均为比较稳定的地基,地面振动基本为低频段,故选择低频测振仪,应用时参考棱镜和低频测振仪刚性连接。NIM-3A 型绝对重力仪选用的测振仪为VSE-311M,测量频率为0.03~70 Hz,输出灵敏度(速度)为2×5 000 V/(m·s-1),分辨率(速度)约为1×10-5Gal。
电气框图如图4 所示。被测落体下落的瞬间,干涉条纹采集系统和振动采集系统接收到同一触发信号,分别对干涉条纹(被测落体相对于参考棱镜的位移)和地面振动(参考棱镜相对于地球的位移)进行采集。为保证采集的干涉条纹和地面振动信号同步,两系统利用同一时间频率标准铷钟作为时钟源。干涉条纹和振动信号采集完成后由上位机进行处理,利用图3 所示的位移补偿方法得到被测落体自由下落的位移,并与记录的时间拟合得到重力加速度g。

图4 测振补偿法的原理框图Fig.4 Principle block diagram of vibration compensation method
4.2 性能测试
在振动较大的地基进行重力测量时,如中国计量科学研究院和平里院区,振动补偿后A 类测量不确定度(即算术平均值的实验标准差)为振动补偿前的1/10。在振动较小的地基上测量时,如中国计量科学研究院昌平院区重力台站(远离市区,周围环境及其安静,点位采用独立地基设计),振动补偿后A 类测量不确定度为补偿前的1/4。图5 为NIM-3A 型绝对重力仪在中国计量科学研究院昌平院区重力台站进行测量时的现场照片。图6 为测量数据,振动补偿前测量数据分散于±500 μGal 内(图6(a)),A 类测量不确定度为5.2 μGal;振动补偿后测量数据大部分在±150 μGal 内(图6(b)),A 类测量不确定度仅为1.3 μGal。振动补偿前后的测量结果偏差在2~3 μGal,在测量不确定度范围内,所以振动补偿后未出现系统偏差。

图5 NIM-3A 型绝对重力仪(注:在中国计量科学研究院昌平院区重力台站进行重力台站加速度测量)Fig.5 NIM-3A absolute gravimeter(Note:NIM-3A is working at gravity site in Changping campus of National Institute of Metrology)


图6 中国计量科学研究院昌平院区重力台站NIM-3A 型绝对重力仪振动补偿前后的测量数据对比(绿色圆点为振动补偿前后未超出3σ 剔除的数据,灰色圆点为振动补偿后超出3σ 剔除的数据)Fig.6 Datum of NIM-3A at gravity site in Changping campus of National Institute of Metrology(Green dots are the datum not exceeding 3 sigma and grey dots are the datum exceeding 3 sigma with vibration compensation)
5 测振补偿法改进
若将测振传感器采集到的振动信号不进行任何处理,直接补偿到干涉法所测的落体下落位移(被测落体相对于参考棱镜的位移)上,由于测振传感器的频率响应特性(见图7),采集到的振动信号不够完备:一是频率范围内两侧信号的幅值有一定的衰减,使得位移补偿不足;二是两侧信号存在一定的相移,使得与干涉法同步测得的落体下落位移存在一定的相位差。可见测振传感器的频率响应特性直接影响振动补偿效果,本文利用传递函数测试及反演技术来提高测振传感器所测的振动信号,最终改善振动补偿效果。
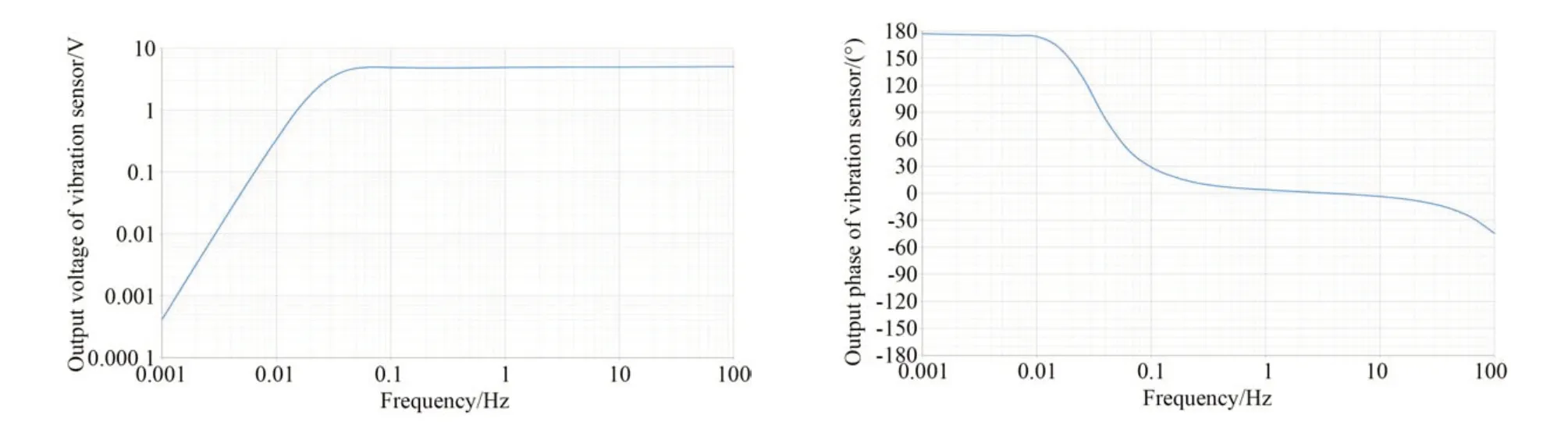
图7 低频测振传感器VSE-311M z 轴方向的频率响应特性Fig.7 Frequency response characteristic of VSE-311M in z axis
5.1 传递函数测试和反演技术
传递函数测试原理如图8 所示。其中,x(t)为测振传感器时域输入信号,y(t)为测振传感器时域输出信号。首先对x(t)和y(t)进行快速傅里叶变换(Fast Fourier Transform,FFT)得到对应的频域信号X(f)和Y(f),再对两个频域信号进行处理,得到测振传感器某个频率点(k点)的幅频和相频特性。将频率范围内所有频率点的幅频和相频特性存入传递函数数据文件中,供实 时控制与反演时使用。

图8 传递函数测试原理Fig.8 Principle for transfer function test technology
在测振传感器测量地面振动时,首先对振动信号的时域波形进行数据采集(DAQ)得到信号的数字序列,经窗函数处理后,根据传递函数测试原理得到的测振传感器传递函数曲线进行实时控制和反演,再经窗函数复原成无缝连接的振动信号真实原始波形和数据,过程如图9 所示。

图9 传递函数反演原理Fig.9 Principle for transfer function inversion
5.2 振动信号处理
利用低频测振传感器VSE-311M 的频率响应特性(图7)和5.1 中提及的传递函数测试和反演技术对测振传感器采集的振动信号进行处理。
图10 所示为在中国计量科学研究院昌平院区21 号楼地下一层比对大厅的隔振地基上采集的振动信号。从图中可以看出,应用传递函数反演技术前后两个振动位移信号的偏差在纳米量级,可带来重力加速度0.1 μGal 的偏差;应用传递函数反演技术后振动信号更加接近参考棱镜实际受到的振动,振动补偿效果更好,最终得到的重力加速度更加准确。
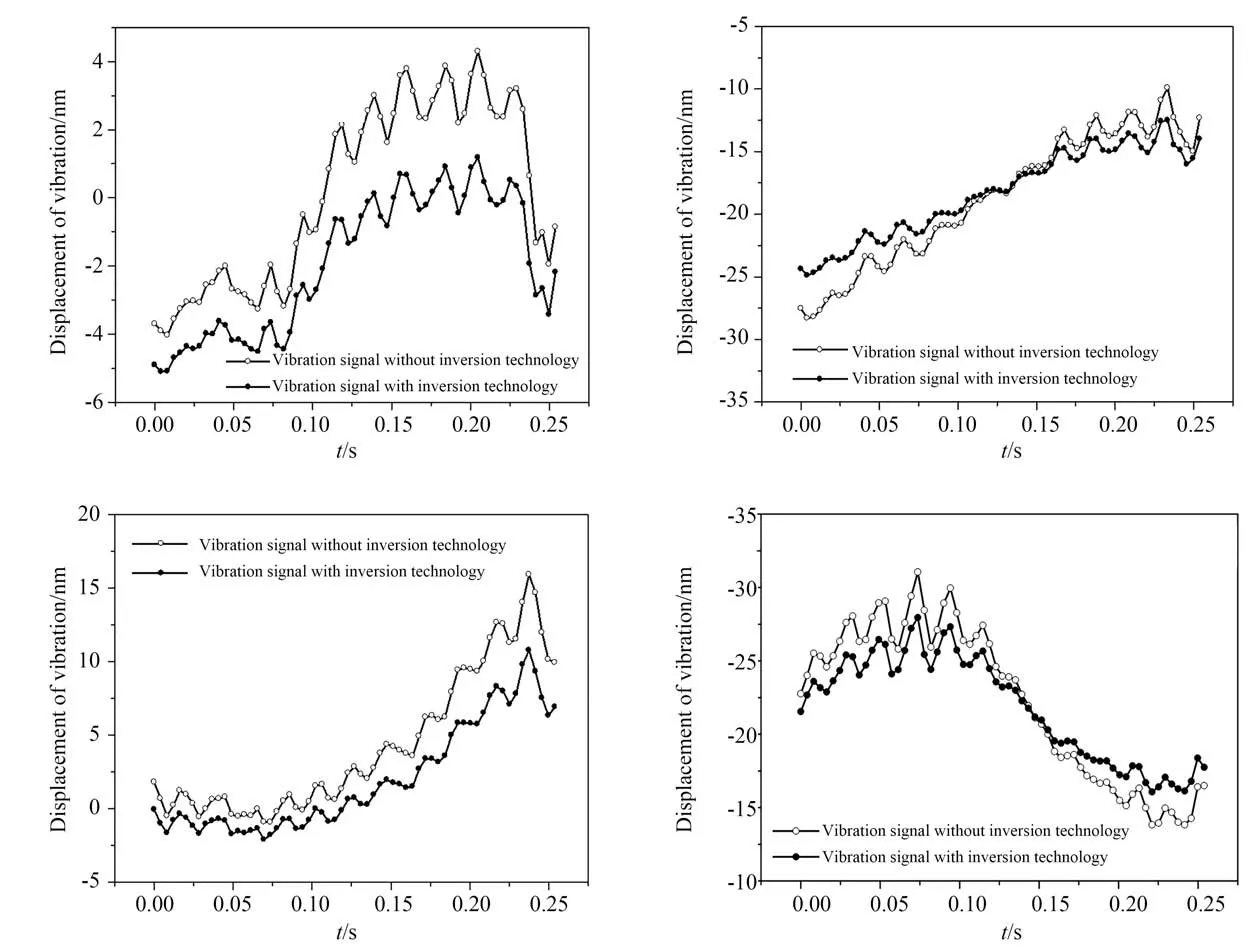
图10 采用传递函数反演技术前后的振动位移信号Fig.10 Vibration displacement signals without and with transfer function inversion technology
5.3 性能测试
在中国计量科学研究院昌平院区重力台站进行测试,振动补偿后A 类测量不确定度为补偿前的1/7.8。图11 为测量数据,振动补偿前测量数据分散于±500 μGal 内(图11(a)),A 类测量不确定度为5.5 μGal;振动补偿后测量数据大部分分散于±70 μGal 内(图11(b)),A 类测量不确定度仅为0.7 μGal。振动补偿后潮汐符合图见图12。振动补偿前后的测量结果有1~2 μGal 的偏差,在测量不确定度范围内,所以改进后的振动补偿未出现系统偏差。
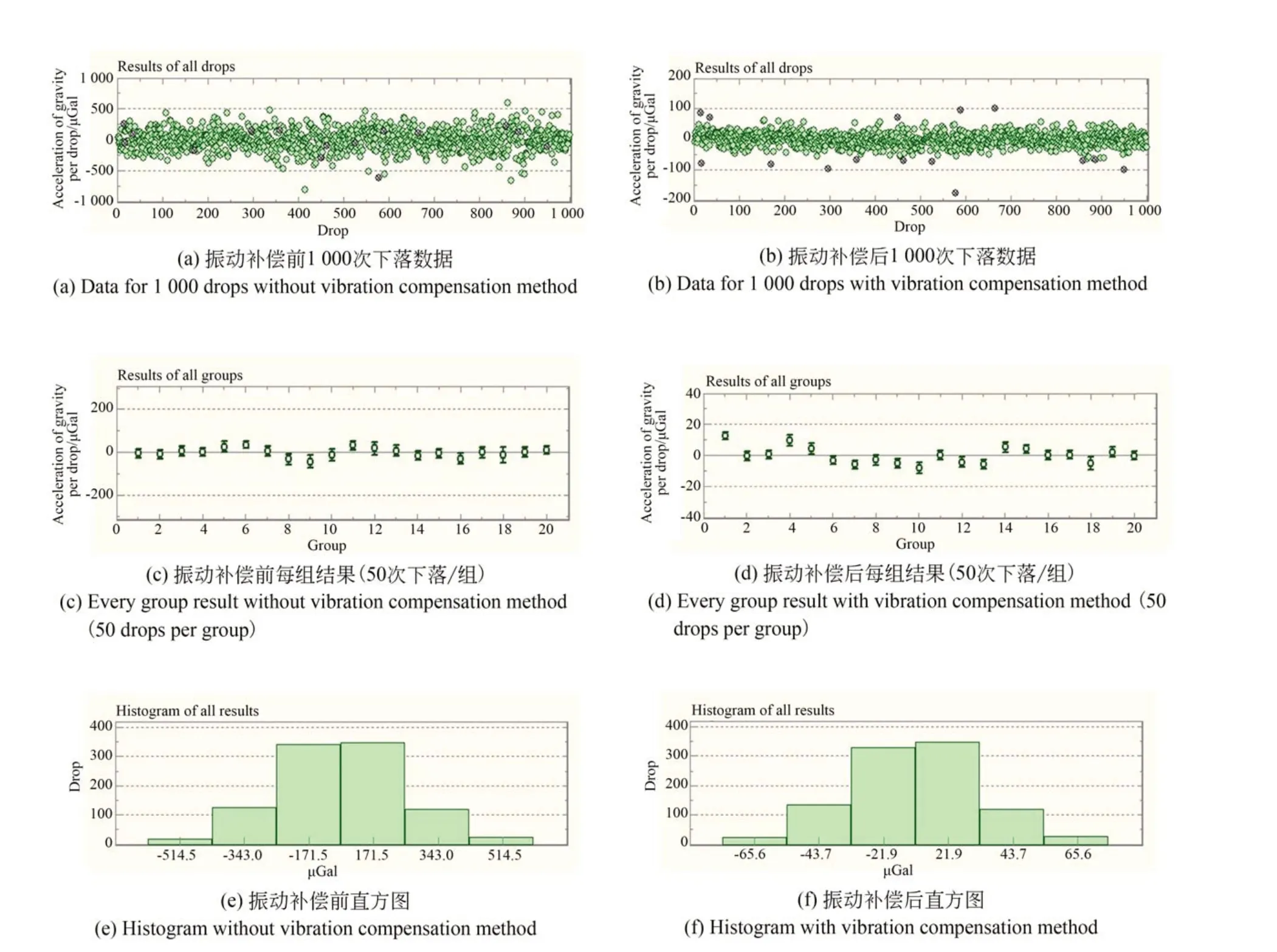
图11 中国计量科学研究院昌平院区重力台站NIM-3A 型绝对重力仪振动补偿前后测量数据对比(改进后)(绿色圆点为振动补偿前后未超出3σ 剔除的数据,灰色圆点为振动补偿后超出3σ 剔除的数据)Fig.11 Datum of NIM-3A at gravity site in Changping campus of National Institute of Metrology after improment(Green dots are the datum not exceeding 3 sigma and grey dots are the datum exceeding 3sigma with vibration compensation)

图12 潮汐符合图Fig.12 Measurement results with tide
在环境噪声(振动)较大的测点上测量时,改进后的振动补偿法对测量A 类不确定度也有很好的优化效果。图13 为在天津某工地测量得到的数据,单次下落结果的分散性由振动补偿前的±20 000 μGal 优化为振动补偿后的±2 000 μGal,A 类 不 确 定 度 由264.8 μGal 变 为17.6 μGal(1/15 倍)。振动补偿前后的测量结果有10 μGal 以内的偏差,在测量不确定度范围内,所以振动条件不佳的情况下改进后的振动补偿未出现系统偏差。

图13 天津某工地(地面振动较大)NIM-3A 型绝对重力仪振动补偿前后测量数据对比(改进后)(绿色圆点为振动补偿前后未超出3σ 剔除的数据,灰色圆点为振动补偿后超出3σ 剔除的数据)Fig.13 Datum of NIM-3A at gravity site at construction site in Tianjin after improment(Green dots are the datum not exceeding 3 sigma and grey dots are the datum exceeding 3sigma with vibration compensation)
由此可见,振动补偿法很好地减小了地面振动对实验数据的影响,缩小了多次测量实验数据的分散性,优化了测量结果的A 类不确定度。改进后振动补偿法使得地面振动采集更精确,进一步提高了单次测量结果的准确性,缩小了测量实验数据的分散性,降低了测量结果的A 类不确定度(7.8 倍)。
2013 年9 月,采用测振补偿法的NIM-3A 型绝对重力仪代表我国参加了由瑞士联邦计量院(Federal Institute of Metrology,METAS)主办的第九届国际绝对重力仪比对ICAG-2013。比对结果表明,NIM-3A 型绝对重力仪的测量结果偏离关键比对参考值(Key Comparison Reference Value,KCRV)1.5 μGal,标 准 不 确 定 度 为5.3 μGal。该结果已在国际计量局网站上公布[27],见图14。2017 年10 月,NIM-3A 型绝对重力仪又代表我国参加了第十届国际绝对重力仪比对ICAG-2017,其 比 对 结 果 见 图15[28],NIM-3A 型绝对重力仪的测量结果偏离KCRV 值0.4 μGal,标准不确定度为3 μGal。
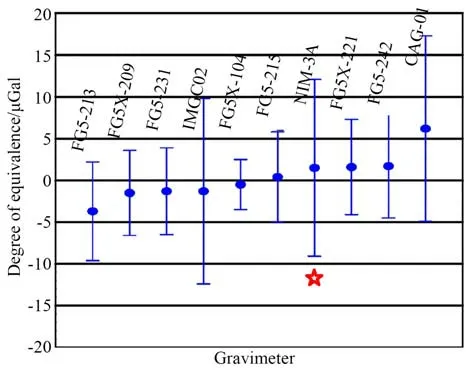
图14 ICAG-2013 关键比对结果Fig.14 Results of ICAG-2013

图15 ICAG-2017 关键比对结果Fig.15 Results of ICAG-2017
6 结 论
地面振动是高精度绝对重力测量最主要的影响因素。本文提出的振动补偿法有效地降低了地面振动对测量结果的影响,优化了测量数据的分散性。实验结果表明:改进后的振动补偿法使得绝对重力仪测量结果的A 类不确定度优化了7.8 倍,未出现系统偏差。
