基于改进差分进化算法的机器人运动学参数标定

姜一舟，于连栋，2*，常雅琪，贾华坤，赵会宁

（1. 合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009；2. 中国石油大学 控制科学与工程学院，山东 青岛 250000）

1 引 言

工业机器人通常具有较高的重复定位精度，但其定位精度却很差［1］。机器人的误差源分为运动学误差和非运动学误差。由于制造和装配导致实际运动学参数与其标称值的偏差称为运动学误差，运动学误差约占总定位误差的90%［2］。因此，运动学参数标定是提高机器人定位精度的重要途径。运动学参数标定分为4 个步骤：建模、测量、识别、补偿或校正［3］。

机器人运动学模型是运动学参数标定的基础，运动学模型应满足运动学参数标定的三个基本要求：完备性、连续性和非冗余性［4-6］。POE（Product of Exponentials）模型为机器人运动提供了完整的几何化和参数化表示，从而大大简化了机器人机构的运动学分析。有研究对POE 模型参数的可辨识性进行了分析，结果表明，POE模型能够满足连续性、完整性和非冗余性的要求［7］。因此，它被认为是理想的机器人运动学建模方法，并被广泛应用［8］。本文采用POE 模型完成了机器人运动学建模，用于六自由度机器人的运动学参数标定。

标定算法在机器人标定过程中起着至关重要的作用。最常用的标定算法是最小二乘算法，如高斯-牛顿算法和LM（Levenberg-Marquardt）算法［9］。LM 算法具有良好的抗干扰能力和全局优化能力，但需要标定参数的初始理论值与实际值接近时才能有较好的标定精度，这限制了算法的应用。差分进化（Differential Evolution，DE）算法［10-11］是一种高效、高精度的优化算法，但容易出现局部收敛，影响运动学参数的标定精度。当种群收敛到目标函数的局部最优值，种群粒子失去多样性，此时算法进展缓慢或者根本不进行［12］。为了提高标定精度，本文提出了一种改进的 差 分 进 化（Modified Differential Evolution，MDE）算法，应用于机器人运动学参数标定。该算法利用Metropolis 接受准则在搜索空间中探索更多的区域以获得更好的全局收敛性。同时，利用种群多样性评价函数评价种群粒子的聚集程度，当种群多样性低于一定阈值时进行二次变异操作。该方法可以有效地提高算法的优化能力和运动学参数的标定精度。

2 运动学模型

2.1 运动学建模

基于旋量理论的POE 模型提供了机器人运动的几何和参数化表示，从而大大简化了机器人机构的运动学分析。

对于旋转关节，从连杆i－1 到连杆i的连杆变换矩阵可以描述为：

qi=[qxi，qyi，qzi]，表 示 基 坐 标 系 中 各 轴 原 点 的 坐标；wi=[wxi，wyi，wzi]，为 各 旋 转 轴 在 基 坐 标 系中的方向向量；ξi为关节旋量的旋量坐标。

本文所用六自由度机器人的机构简图如图1所示。根据以上公式，机器人的正运动学表示为：

图1 六自由度机器人机构简图Fig. 1 Link frames of used 6-DOF robot

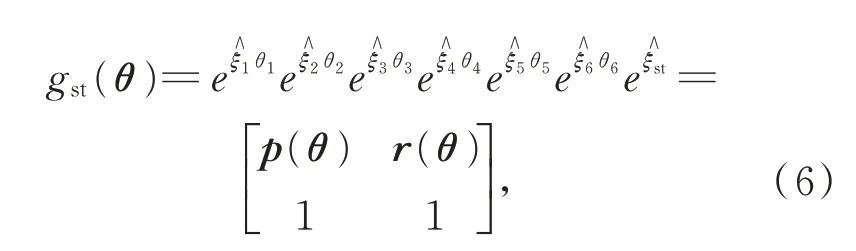
其中：ξˆst为机器人初始旋量，r(θ)为机器人末端位置坐标。

由于加工误差、装配误差和机械变形等原因，机器人的运动学参数通常与设计值有偏差。因此，如图2 所示，定义在关节处的坐标系会稍微偏离其理想位置。

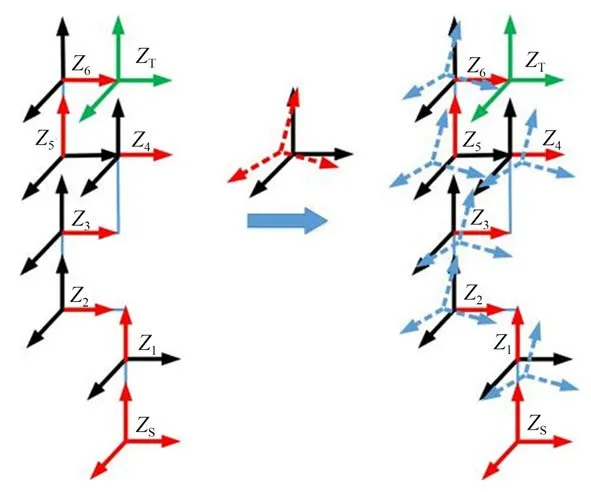
图2 六自由度机器人坐标系示意图Fig. 2 Schematic diagram of 6-DOF robot structure after coordinate transformation

在本文中，理论运动学参数是已知量。当只考虑运动学参数误差时，机器人的实际位置坐标可以表示为：

共42 项待辨识运动学参数误差。

作者简介：卢欢，女，江西铜鼓人，江西省吉安市吉州区古南二小，中小学二级教师，本科学历，研究方向：小学数学课堂教学有效性。

2.2 距离误差模型

距离精度是工业机器人的一个重要性能指标［13］。本文采用距离精度衡量机器人运动学参数标定精度，并利用距离误差模型对运动参数进行标定［14］。

如图3 所示，相邻两点p与p＋1 之间距离的平方可以表示为（在任意两点的情形，只需将式（9）中的p＋l 以q（q≠p）代替即可）：

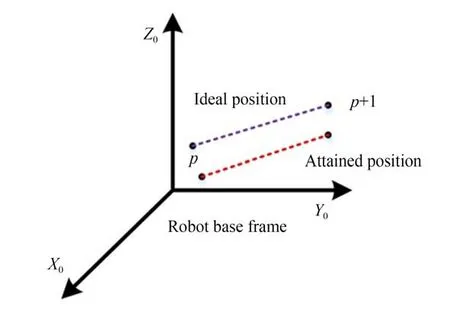
图3 距离误差模型Fig. 3 Distance error model

其中：lm(p，p＋1)表示采样点实际位置之间的距离，本文采用激光轨迹测量实际位置坐标；ltheo(p，p＋1)表示采样点期望位置坐标之间的距离，采样点期望位置坐标根据运动学模型计算得到。

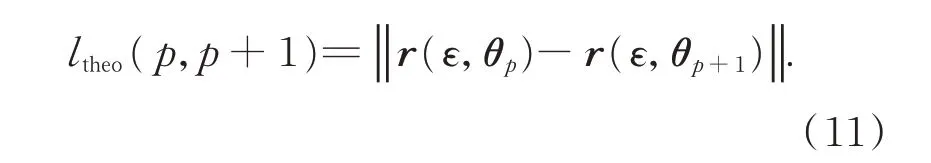
因此，标定过程中使用的目标函数可以表示为：

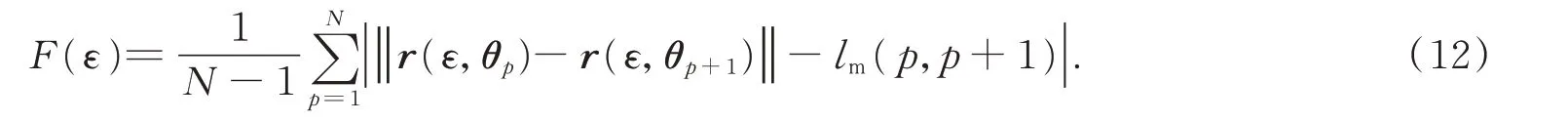
3 标定算法

标定算法用于优化目标函数，求解运动学参数误差［15］。差分进化算法是一种基于种群差异进行高效优化的启发式算法。随着算法的迭代计算，种群粒子会收敛为最优粒子，种群的多样性会下降，容易陷入局部收敛。为了保证算法的全局收敛性和最终定标精度，必须提高种群的多样性，防止算法过早收敛。

3.1 差分进化算法

差分进化算法包括变异操作、交叉操作和选择操作。种群个体εi={Δwi，Δqi}按公式（13）进行初始化：

对种群个体按公式（12）计算目标函数，并且选择使目标函数值最小的最优解εgbest。如果F(εgbest)＞0.1 mm，或迭代次数小于预设次数，继续执行变异操作。个体变异操作的公式为：

其中CR是一个在［0，1］内的实值交叉概率因子，CR影响搜索过程的收敛速度和鲁棒性。按式（17）执行交叉操作，生成测试个体εT i。在本文中，为了保证较快的收敛速度，CR=0.9。

然后，基于贪心搜索策略完成选择操作：

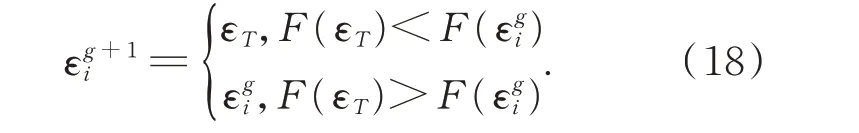
差分进化算法的伪代码如图4 所示。

图4 差分进化算法流程Fig. 4 Flow chart of differential evolution algorithm

3.2 Metropolis 接受准则

将Metropolis 接受准则与DE 算法相结合应用于选择操作中，可以使算法以一定的概率接受恶化解，从而使算法具有逃脱局部极值和避免过早收敛的全局优化能力［17-19］。以式（19）代替式（18）完成选择操作，即：

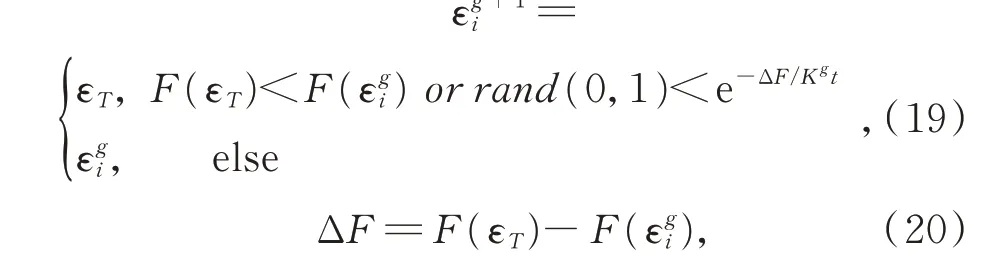
式中：t为初始退火温度，K∈(0，1)为冷却系数，g为迭代次数。

迭代开始时，算法直接接受较优解，以较大概率接受较差解，避免种群粒子过早聚集，陷入局部优化。随着迭代次数的增加，算法接受较差解的概率降低，从而保证了算法在后续迭代中具有更好的优化速率。

3.3 种群多样性评价函数

差分进化算法的全局优化能力与种群的多样性有关［20］。改进差分进化算法将种群多样性描述为种群粒子的聚集程度。随着迭代次数的增加，粒子逐渐聚集，种群多样性减少，导致算法陷入局部优化解。因此，采用一种避免种群粒子过早聚集的方法，可以有效提高全局优化能力。

本文提出了一个种群多样性评价函数来监测种群多样性，当种群低于某一阈值时进行二次变异操作以避免陷入局部优化，即：

改进差分进化算法流程如图5 所示。利用种群多样性评价函数，在每次迭代中评估粒子种群的聚集程度，并对过度聚集的粒子进行两次突变，从而有效提高了差分进化算法的全局优化能力和最终标定精度。

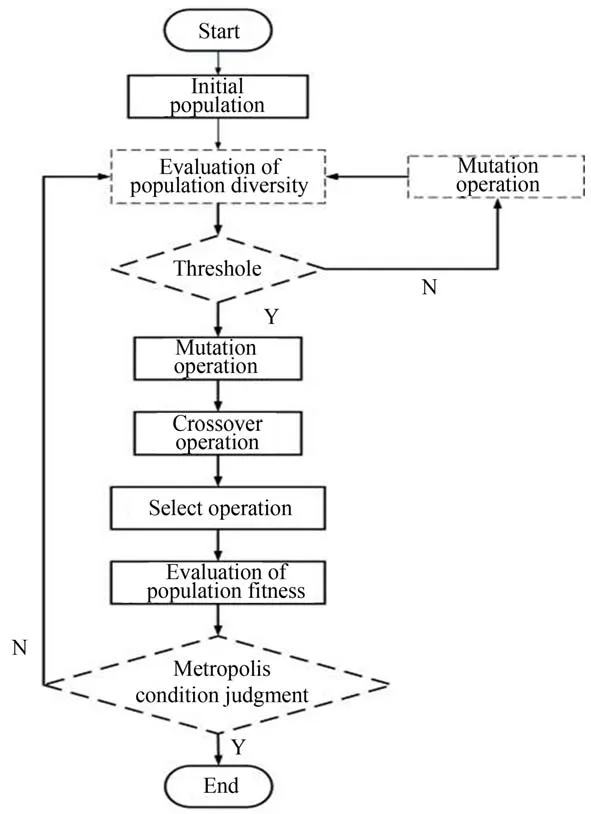
图5 改进差分进化算法流程Fig. 5 Flow chart of modified differential evolution algorithm

4 实验与仿真

实验系统如图6 所示。实验对象为六自由度串联机器 人（Universal robot 5，Universal Robots，Danmark）。在机器人末端执行器上的指定位置固定有靶球。使用精度为0.005 mm/m 的激光跟踪器（API T3，Automated Precision Inc，USA）测量机器人末端的位置坐标。

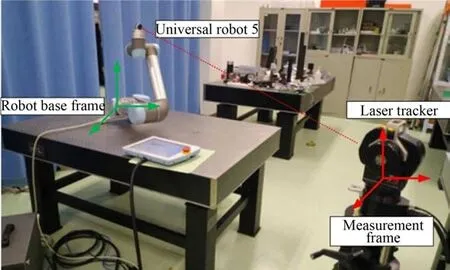
图6 机器人运动学参数标定实验装置Fig.6 Experimental setup for calibration of robot kinematic parameters

4.1 仿 真

在理论运动学参数中加入随机参数误差作为实际参数进行仿真。采用500 组关节变量和位置坐标数据进行运动学参数标定，采用另外100组测量数据进行验证。通过比较LM 算法、DE算法和提出的MDE 算法的仿真结果，验证了改进算法的有效性。采用不同算法得到的运动学参数误差如表1 所示。标定后的距离误差结果如图7 和表2 所示。仿真实验结果表明，与LM 算法和DE 算法相比，MDE 算法的运动学参数标定效果最好。该算法可以有效地提高机器人的定位精度。最大距离误差由2.392 0 mm 减小到0.249 3 mm，平均误差由0.880 5 mm 减小到0.080 5 mm。

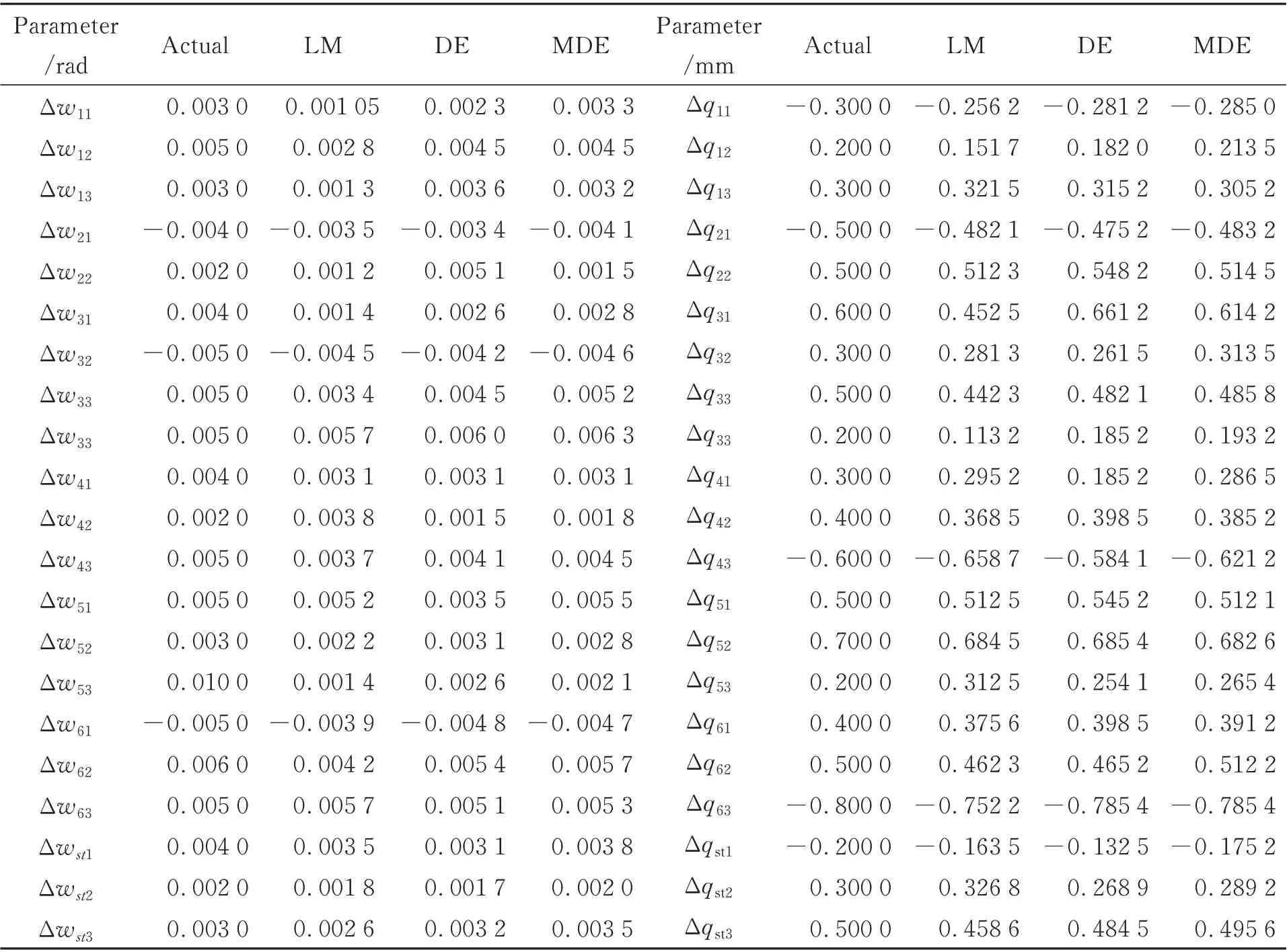
表1 运动学参数辨识结果Tab. 1 Identification results of kinematic parameters

表2 仿真实验结果Tab.2 Simulated calibration results （mm）

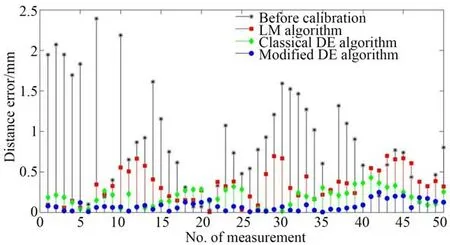
图7 仿真实验结果Fig.7 Simulation results

4.2 标定实验

在实验过程中，通过测量机器人在工作空间内的500 个关节变量和位置坐标数据，对机器人参数进行标定。选择的采样点在应使相应的关节变量能够覆盖机器人的关节工作范围。同时测量了100 个采样点，用于标定后精度的验证。

在实验过程中，采用LM、DE 和MDE 算法识别机器人的运动学参数误差。实验结果如图10 和表3 所示。标定前，受运动学参数误差的影响机器人定位精度较低，最大距离误差为4.431 0 mm，平均距离误差为1.148 8 mm。经过LM 算法、经典DE 算法和MDE 算法的标定，运动学误差降低，机器人的定位精度得到了显著提高。如图8 所示，采用MDE 算法标定后，机器人的距离误差最小。

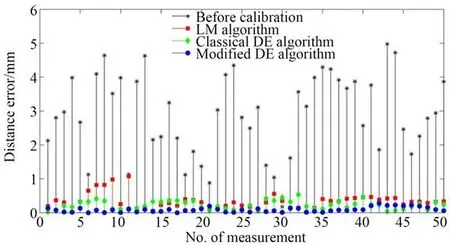
图8 运动学参数辨识实验结果比较Fig. 8 Comparison of kinematic calibration experimental results

图9 比较了经典DE 算法和MDE 算法的收敛能力，图10 比较了迭代优化过程中的种群多样性变化情况。如图9 和图10 所示，经典的DE 算法比MDE 算法收敛得早，同时种群多样性降低到1 左右。MDE 算法使种群多样性保持在1 左右，避免了算法提前收敛。因此，MDE 算法表现出更好的优化能力。标定实验结果见表3，最大距离误差从4.977 mm 到0.280 7 mm，平均误差从2.906 0 mm 减少到0.095 2 mm。

图9 全局收敛性比较Fig.9 Comparison of global convergence

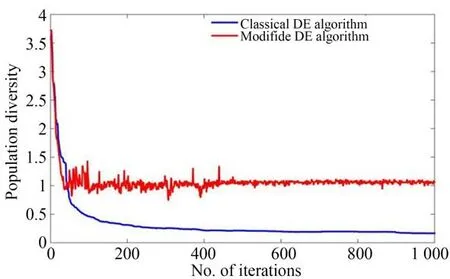
图10 种群多样性变化Fig.10 Changes in population diversity

表3 运动学参数标定结果Tab.3 Experimental calibration results （mm）

5 结 论

为提高运动学参数标定精度，本文提出了一种MDE 算法。该算法在选择操作中结合了Metropolis 接受准则，同时采用种群多样性评价函数来监测种群粒子的聚集度，在种群低于某一阈值时进行二次变异操作，以避免算法陷入局部优化。本文采用六自由度串联机器人和激光跟踪仪进行了运动学参数标定的仿真和实验。经过标定，机器人的平均距离误差由2.906 0 mm（校准前）降低到0.095 2 mm。通过标定实验与DE算法和LM 算法进行比较，验证了MDE 算法的优越性。