柱面微透镜阵列的精密磨削

叶 震，姚 鹏*，于世孟，张仙朋，黄传真

（1. 山东大学 机械工程学院 先进射流工程技术研究中心，山东 济南 250061；2. 高效洁净机械制造教育部重点实验室，山东 济南 250061）

1 引 言

柱面微透镜阵列元件表面的微结构可以实现对入射光的扩散，光束整形，光线均匀分布［1-2］和聚焦等调制，进而实现特定的光学功能，在军事、民用、天文等领域有着广泛的应用。周叶、祝启欣等［2］采用微柱面镜阵列光学元件对高斯激光束进行调制，实现了高斯光束的均匀化，获得了均匀的线光斑。张凯华、董连和等［3］通过柱面微透镜阵列有效提高了光电流和光功率的效率，从而极大地提高了有机发光二级管（OLED）的图像质量。传统的柱面微透镜阵列加工是在超精密磨床上用微小磨具进行超精密磨削，这种方法的加工效率非常低。采用具有微细结构的成形砂轮进行复映法加工能极大地提高加工效率，并且降低加工机床的编程难度。

通过研究砂轮表面磨粒与工件的几何相互作用机理，建立磨削表面的仿真模型，可以有效预测磨削加工后工件的表面质量和加工误差。因此，众多学者开展了磨削仿真研究，并且取得了丰硕的研究成果。Malkin［4］建立了磨削几何学模型，提出磨削深度和接触长度等概念。Nguyen［5］通过实测砂轮表面磨粒的突出高度分布，指出磨粒突出高度呈非正态分布，并且通过数字模拟 技 术 模 拟 了 砂 轮 表 面。Hou 和Komanduri［6］通过概率模型研究磨削过程，提出只有很小部分的磨粒真正参与磨削去除材料，并且得出参与材料去除的磨粒的概率，但是没有进一步研究磨削表面模拟方法。刘月明［7］将磨粒的形状假定成不规则六面体，通过随机振动法模拟砂轮表面磨粒的分布状态。Zhao［8］和费亚［9］等通过数字模拟法模拟砂带的表面形貌，用几何学模拟磨粒去除材料过程，仿真出工件的表面形貌。Zhang 等［10］通过纳米压痕实验得出复相材料中两种相磨削时脆塑转变的临界切深，研究不同切深条件下，磨粒切入工件形成的沟槽的截面形状，进而预测磨削复相材料工件的表面粗糙度，但是没有考虑磨粒的磨削轨迹会发生干涉。Jiang［11］等考虑砂轮跳动误差，通过包络算法模拟多轴磨削过程，成功预测了工件的表面形貌。孙金升等［12］将磨粒有序化排布在砂轮表面，形成表面磨粒结构化砂轮，仿真了结构化砂轮磨削后工件的表面形貌。梁志强等［13］研究螺旋伞齿轮的磨削仿真方法，基于设定好的砂轮的空间运动轨迹模拟磨粒空间轨迹干涉，进行螺旋伞齿轮磨削加工的表面预测，并研究了不同加工参数对表面质量的影响。

综上所述，很多学者开展了磨削仿真和质量预测的研究，但是这些研究大多是针对平面磨削，针对具有微细结构轮廓的成形砂轮的磨削仿真研究则较少。而且这些研究只选取砂轮的局部区域进行砂轮表面的模拟，研究这一区域的磨粒作用于工件表面后形成的工件表面形貌，但是不能反映整体砂轮作用于工件表面后工件的表面形貌。本研究根据实测的砂轮形貌，对具有微细结构的成形砂轮进行整体建模，采用优选的仿真算法模拟磨削后工件的表面形貌，预测了工件的面形误差和表面粗糙度，最后进行磨削实验验证了仿真模型的正确性。

2 微细结构成形砂轮空间形貌建模

2.1 砂轮表面数据的采集

Nguyen［5］等通过实际测量砂轮表面磨粒突出高度的分布状态，发现大部分砂轮的磨粒突出高度都是偏态分布。因此，很多研究者通过实际测量方法来分析砂轮表面磨粒突出高度的分布状态。本文选用600#金属结合剂金刚石砂轮，砂轮直径为200 mm。用基恩士VK-X200 激光共聚焦显微镜采集微细阵列结构砂轮的表面形貌，采用图像自动拼接技术得到大面积表面形貌数据。图1 是采集的微细阵列结构砂轮的表面形貌，采样区域尺寸为2 500 μm×6 180.5 μm，采样间距为2.76 μm。

图1 微细阵列结构砂轮的表面形貌Fig.1 Surface topography of grinding wheel with fine array structure

2.2 砂轮表面磨粒的特征分析

2.2.1 砂轮表面形貌数据处理

采用MATLAB 软件对采集的形貌数据进行分析，区域尺寸是0.5 mm×0.5 mm。砂轮表面形貌数据主要由低频曲率信号、中频信号和高频噪声信号3 部分构成。低频曲率信号表征成形砂轮本身的微结构轮廓，中频信号表征磨粒的突出高度形貌，高频噪声信号主要来源于激光测量的干扰信号和砂轮表面的破碎结构。为了分析磨粒的突出高度分布特征，需要去除低频曲率信号和高频噪声信号，保留中频信号。

本文采用高斯滤波方法进行低频曲率信号的提取和去除。高斯滤波可以实现低频信号和高频信号的分离，由于高斯滤波具有平滑的系统函数，相较于理想滤波器，可以有效避免振铃现象。二维高斯滤波函数g(x，y)和传递函数G(x，y)的定义如下：

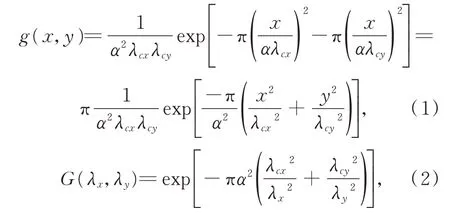
其中：λcx，λcy分别是x，y方向上的截止波长，λx，λy分别是x，y方向上的波长，α=0.469 7。

为了去除噪声信号，本文采用功率谱密度频谱确定噪声信号的截止频率，然后用低通滤波器过滤噪声信号。功率谱密度反映信号在不同频率处的能量强度，功率谱密度的表达式为：

其 中：f是 信 号 的 频 率，N是 采 样 数 量，d0是 采 样长度，j 是虚数单位，s(x，y)是信号的幅值函数。

图2 是去除曲率信号的砂轮表面形貌的功率谱密度函数图像。由于噪声信号的能量占比非常小，从图像中可以看到功率谱密度在f=53 mm－1处基本为零，所以噪声信号的截止频率fc=53 mm－1。采用截止频率为53 mm－1的低通滤波器，就可以去除砂轮表面形貌的噪声信号。

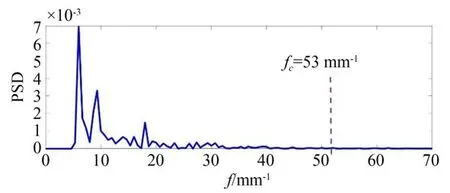
图2 功率谱密度函数图像Fig.2 Functional image of Power Spectral Density（PSD）

通过以上步骤，可以将采集到的砂轮表面的形貌数据进行分解，最后提取磨粒突出高度的形貌。图3 是在频域分解砂轮形貌得到的低频、中频和高频的形貌，图4 是砂轮表面磨粒突出高度分布的形貌。

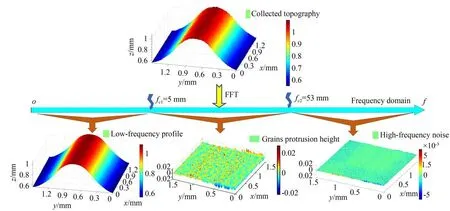
图3 砂轮形貌频域划分以及各个频域范围的形貌Fig.3 Partition of frequency domain and topographies in each frequency range for grinding wheel

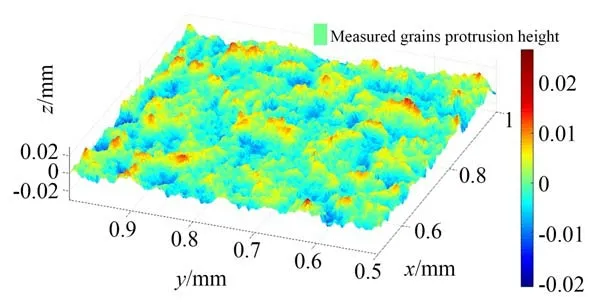
图4 砂轮表面磨粒突出高度分布形貌Fig.4 Topography of protrusion height of grains on grinding wheel surface

2.2.2 砂轮表面磨粒突出高度分布和数学统计参数

砂轮表面磨粒突出高度分布主要分为正态分布和偏态分布两种。图5 是上一节中砂轮表面磨粒突出高度的分布图和正态拟合曲线，从图中可以看出磨粒突出高度分布存在一定的偏度和峰度，所以砂轮表面磨粒突出高度分布为偏态分布。

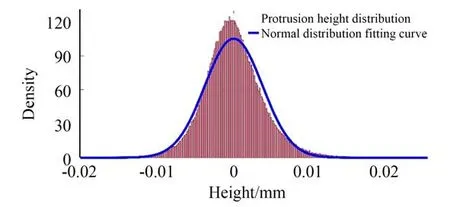
图5 砂轮表面磨粒突出高度的分布和正态拟合曲线Fig.5 Distribution of protrusion height of grains on grinding wheel surface and normality fitting curve

表征表面形貌的数学统计参数［14］主要有平均高度-z，标准差σ，偏斜度Sk，峰度K以及自相关函数R(k，l)。由于砂轮表面的磨粒突出高度分布具有一定的随机性，为了减小误差，使计算的数学统计量更准确地反映磨粒突出高度的分布特征，本文在图1 的砂轮表面形貌上选取4 块0.5 mm×0.5 mm 区域，按照如上步骤进行数据处理和计算数学统计量。4 块区域的数学统计量如表1 所示，从表中可以看出，砂轮各个区域的表面磨粒突出高度分布具有相似性，用4 个区域的数学统计量平均值表征砂轮表面磨粒的突出高度分布。

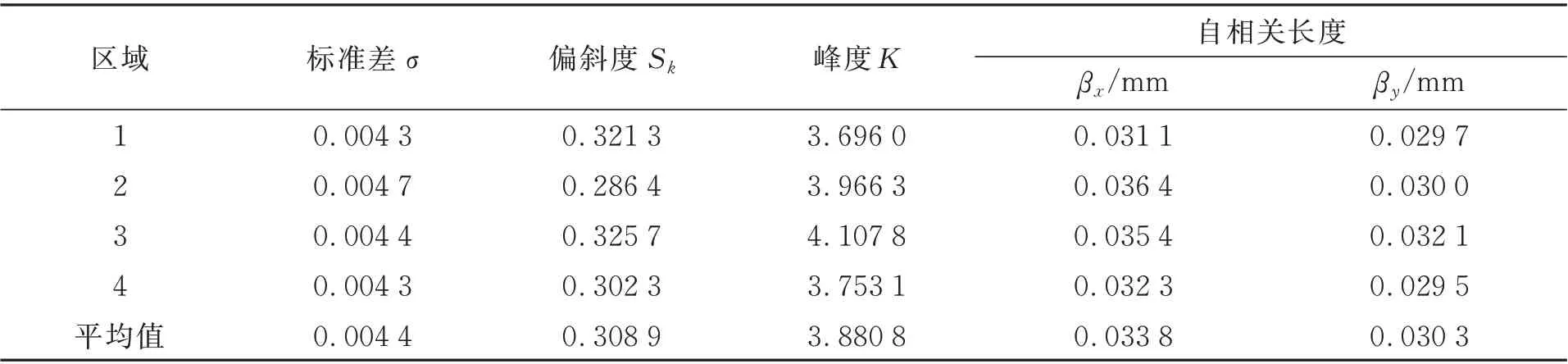
表1 砂轮4 个区域的表面磨粒突出高度分布数学统计量Tab.1 Mathematical statistics of protrusion height of grains in 4 areas on grinding wheel surface

2.3 微细结构成形砂轮整体表面形貌的重构

2.3.1 砂轮表面磨粒突出高度形貌模拟

由2.2.2 节内容可知，砂轮磨粒突出高度表面是偏态分布表面，由此得出表征砂轮表面磨粒突出高度分布的数学统计量。本文主要采用数字模拟技术得出和实测砂轮磨粒突出高度表面有相同偏态分布特征的粗糙表面。

二维数字低通滤波器可以将随机生成序列转化为有指定自相关函数的序列，用卷积形式可以表示为：

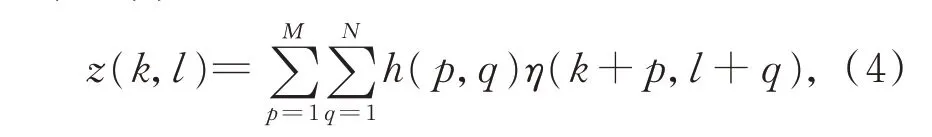
其中：η(k，l)是输入的M×N随机序列，h(p，q)是数字滤波器序列，z(k，l)是输出序列。

数字滤波器序列h(p，q)和输出序列的自相关函数相关联。假设输出序列z(k，l)具有理想的指数型自相关函数，表示为：

其中βx和βy分别是x和y方向的自相关长度。

Hu 等［15］提出一种基于快速傅里叶变换（Fast Fourier Transform，FFT）的滤波算法。Johnson转换系统可以将正态分布的序列转化为具有特定偏斜度和峰度的偏态分布序列，并且不改变序列的自相关性。Johnson 变换的通式如下：式中：η为正态随机序列，η'为具有指定偏度和峰度的偏态随机序列，γ和δ是形状参数，ε为中心偏移量，λ为比例因子。γ，δ，ε和λ由指定的偏度Sk和峰度K确定，具体参考Hill［16］和Johnson［17］的文章。

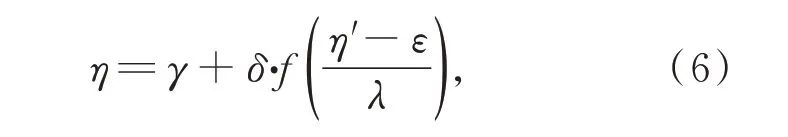
针对符合不同条件的偏度Sk和峰度K，Johnson 转换系统可以分为有界系统、无界系统和对数正态系统3 种类型，如表2 所示。通过判断Johnson 转换类型确定Johnson 转换公式后，需要对变换公式求反，以实现正态分布序列到偏态分布序列的变换。

表2 Johnson 转换的三种类型Tab.2 Three types of Johnson transform

生成具有指定偏度、峰度和自相关性的砂轮表面磨粒突出高度形貌的步骤如下：利用随机序列发生器生成具有正态随机分布的一组序列；由于Johnson 转换基本不改变自相关性，而滤波系统对偏度和峰度的改变较大，所以需要首先对随机序列进行二维数字滤波，使序列具有指定的自相关性；然后对序列进行Johnson 转换，赋予序列指定的偏度和峰度。生成的序列即为重构的砂轮表面磨粒突出高度形貌。形貌生成的算法流程如图6 所示。

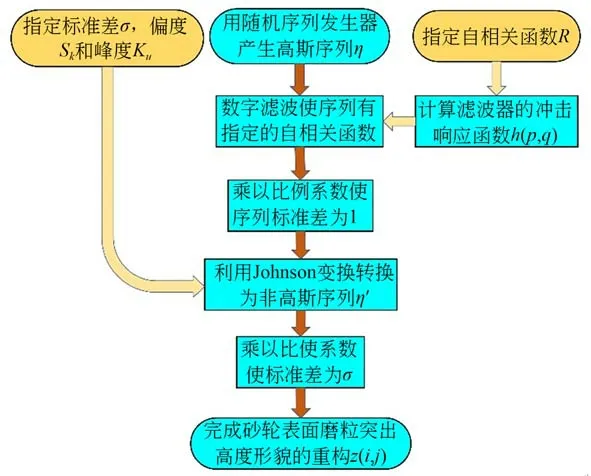
图6 重构砂轮表面磨粒突出高度形貌的流程Fig.6 Flow chart for reconstruction of protrusion height of grains on grinding wheel surface

按照如上步骤根据实测的砂轮表面磨粒突出高度分布的数学统计参数模拟出有相同分布的表面。图7 是实测的砂轮表面磨粒突出高度形貌和模拟的表面形貌。表3 是实测的砂轮表面磨粒突出分布的数学统计参数和模拟表面的数学统计参数。从图7 可以看出，实测的砂轮表面磨粒突出高度形貌和模拟表面有着相似的分布特征。从表3 可以看出，模拟表面的数学统计参数和实测的砂轮表面磨粒突出分布的数学统计参数存在一定的误差，这是因为数字模拟方法具有一定的随机性，并且Johnson 转换也会对自相关性产生微小的影响，但是误差控制在5%的范围内，验证了模拟砂轮表面磨粒突出高度分布的模型的正确性。

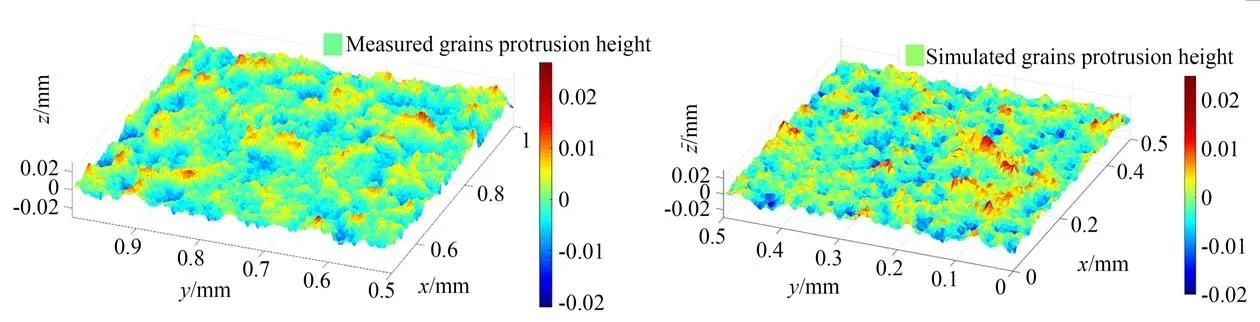
图7 实测和模拟的砂轮表面磨粒突出高度形貌Fig.7 Measured and simulated topography of protrusion height of grains in grinding wheel surface

表3 实测和模拟的砂轮表面磨粒突出分布的数学统计参数对比Tab.3 Mathematical statistics of measured and simulated protrusion height of grains on grinding wheel surface

2.3.2 合成法模拟砂轮整体形貌

为了重构砂轮表面的整体形貌，先将砂轮沿着圆周方向展开到平面，在平面上构造砂轮表面形貌。由于砂轮的实际形貌非常复杂，需要进行合理的简化。本文将沿圆周方向展开的砂轮的形貌分为三部分，第一部分是砂轮的轮廓形貌，第二部分是砂轮径向跳动误差，第三部分是砂轮表面磨粒突出高度形貌。砂轮的轮廓形貌可以通过石墨复印法［18］采集，用金刚石砂轮磨削精细石墨块，可以将砂轮的轮廓复印在石墨块上，然后测量石墨块上沟槽的轮廓形貌，采集到的轮廓形貌就是砂轮的轮廓。砂轮的径向跳动误差通过高精度激光位移传感器测量，砂轮磨削实验中需要将砂轮的跳动误差控制在2 μm 内，本文将跳动误差简化为砂轮圆周上10 个周期幅值为2 μm的正弦曲线。砂轮表面磨粒突出高度形貌用2.3.1 节中的数字模拟方法进行重构，通过Johnson 转换和滤波系统生成面积为L×W的非正态分布表面。其中，L是砂轮的周长，L=2π·R，R是砂轮半径，W是砂轮的宽度。

图8 是平面展开的砂轮的轮廓形貌、径向跳动误差和表面磨粒突出高度以及将3 部分形貌相加形成的砂轮表面的完整形貌。图9 是模拟和实测的砂轮形貌的截面对比，可以看出，模拟和实测的砂轮截面形貌的吻合度很高。

图8 （a）展开在平面的砂轮轮廓形貌；（b）展开在平面的砂轮径向跳动误差；（c）砂轮的磨粒突出高度形貌；（d）将以上三部分形貌合成得到的在平面展开的砂轮形貌Fig.8 （a）Grinding wheel profile unfolded on plane；（b）Radial run-out error of grinding wheel unfolded on plane；（c）Protrusion height of grains in grinding wheel surface；（d）Grinding wheel topography unfolded on plane by combining above three parts

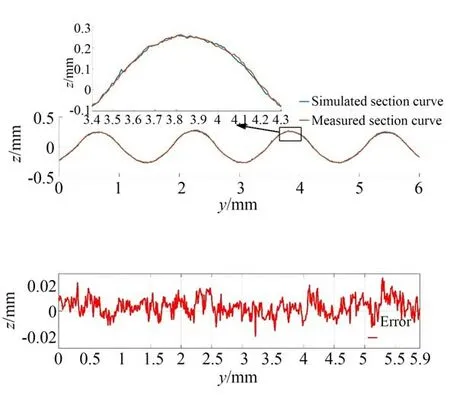
图9 （a）模拟和实测的砂轮表面的截面对比；（b）模拟的砂轮截面和实测截面的差值Fig.9 （a）Section curves of simulated and measured grinding wheel surface；（b）Error of simulated section curve compared to measured one

模拟出砂轮沿圆周方向展开到平面的形貌后，需要通过旋转变换将平面砂轮形貌在圆周方向进行排布，生成砂轮在空间中的整体形貌。图10 是将砂轮的平面形貌按圆周方向排布形成砂轮的空间形貌的示意图。将平面砂轮形貌和平行于yoz的平面形成的截面曲线i（i=1，2，…，M），沿周向依次排布在半径为R的圆柱体表面，截面曲线i的坐标向量矩阵为：

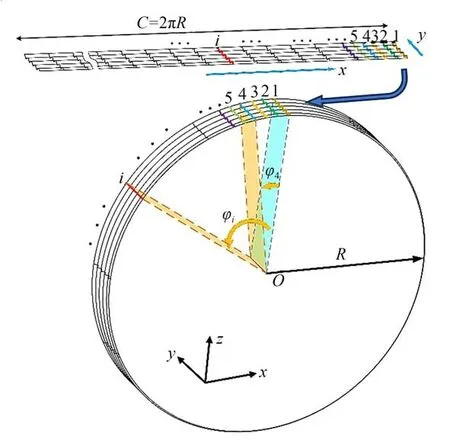
图10 砂轮的平面形貌按圆周方向排布形成砂轮的空间形貌Fig.10 Spatial topography of grinding wheel formed by arraying plane topography along peripheral direction

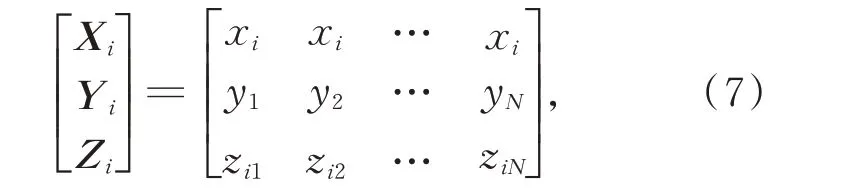
其中：xi，yj和zij分别是构成砂轮平面形貌的x轴，y轴和z轴的坐标值；i=1，2，…，M；j=1，2，…，N，M和N分别是x方向和y方向上的数据点的个数。

首先将截面曲线i置于半径为R的圆柱体的初始截面1'上，然后将截面曲线i逆时针旋转ϕi角度，得到砂轮在圆柱体上的截面曲线i'，截面曲线i'的坐标向量矩阵为：

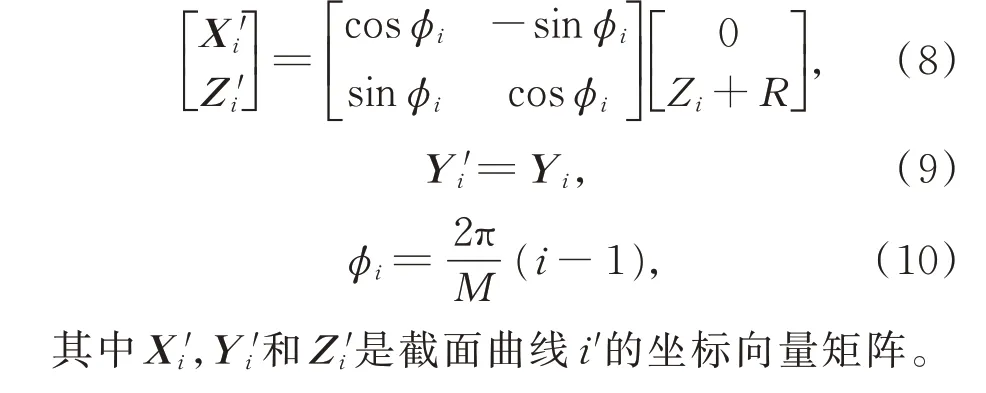
将平面砂轮形貌上的所有截面曲线按照以上算法依次在空间圆柱表面排布，生成砂轮在空间中的整体形貌。砂轮的空间坐标向量矩阵为：

最终模拟得到砂轮在空间的整体形貌，如图11 所示。

图11 模拟的砂轮的整体空间形貌Fig.11 Simulated integral space topography of grinding wheel

3 工件的磨削表面形貌仿真

3.1 磨削运动学模型的建立

磨削工件表面得到的最终形貌是砂轮表面所有磨粒共同作用的结果。将磨削过程简化成几何学模型，在仿真前做以下几点假设：（1）不考虑磨削过程中产生的各种误差因素；（2）假设与砂轮磨粒接触的工件材料被完全去除；（3）不考虑材料塑性流动和脆性断裂去除的影响。

将空间砂轮表面上每个坐标点(x'ij，y'ij，z'ij)视为一颗微小磨粒gij，磨粒gij的运动轨迹如图12所示。实际加工过程中，工件提供x负方向的进给运动，为了方便建模，假设工件固定，砂轮以相同的进给速度反方向进给。

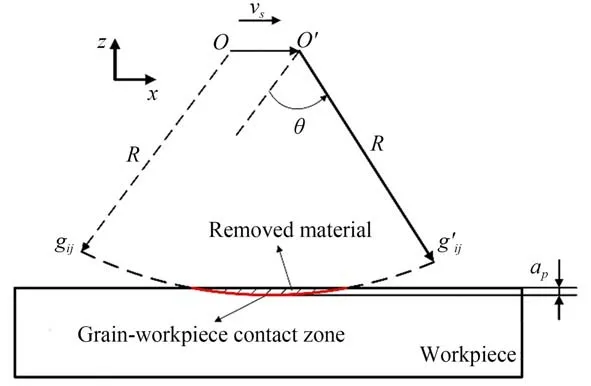
图12 磨粒的运动轨迹示意图Fig.12 Trace of one grinding grain

磨粒gij的运动轨迹方程为：

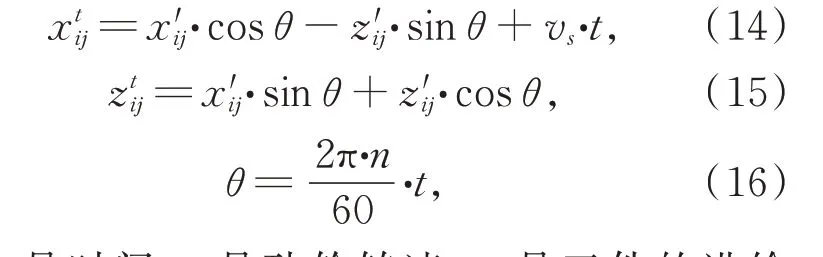
其 中：t是 时 间，n是 砂 轮 转 速，vs是 工 件 的 进 给速度。

3.2 磨粒运动轨迹的离散化

为了将磨粒gij的运动轨迹作用到工件上，在工件表面形成刻划，需要将参数方程表示的磨粒运动轨迹离散到工件坐标系wmn。在砂轮旋转一个周期T=60/n的时间内离散化时间t，由式（14）～式（16）得到磨粒gij的运动轨迹点序列：

其中P是时间t在周期T内取点的个数。

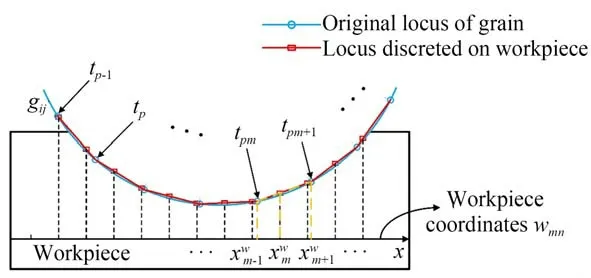
图13 磨粒gij 的运动轨迹离散到工件坐标系的示意图Fig.13 Dispersing trace of grinding grain gij into workpiece coordinate

3.3 磨削表面形貌仿真

磨削工件表面形貌的仿真流程如图14所示。

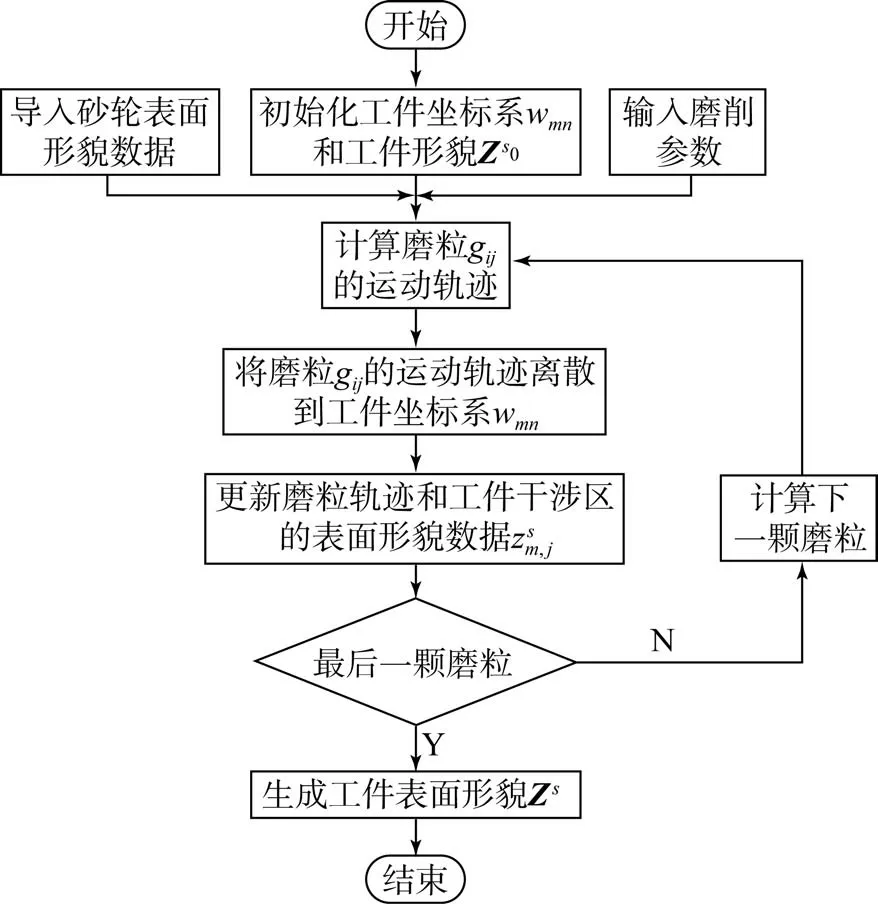
图14 工件磨削表面形貌的仿真流程Fig.14 Simulation flow chart of workpiece grinding surface

4 仿真和实验分析

4.1 实验设备和工件

为了验证仿真结果的正确性，需要进行相同的磨削条件的磨削实验，用实验得到的磨削表面和仿真结果进行比对。

本文的实验机床是超精密平面成形磨床NAS-520X-CNC，主轴转速范围为0～3 600 r/min，机床上下轴和前后轴配备0.1 μm 的高精度光栅尺，全闭环控制，位置控制分辨率达到0.1 μm。采用金属结合剂金刚石砂轮，一次装夹磨削成形，达到相应的面形精度，工件材料是RB-SiC。采用3D 激光共焦显微镜观察RB-SiC 的磨削表面，测量表面粗糙度和面形误差。图15 是柱面微透镜阵列的磨削实验装置。表4 是磨削实验的磨削工艺参数。表5 是RB-SiC 材料的机械性能参数。

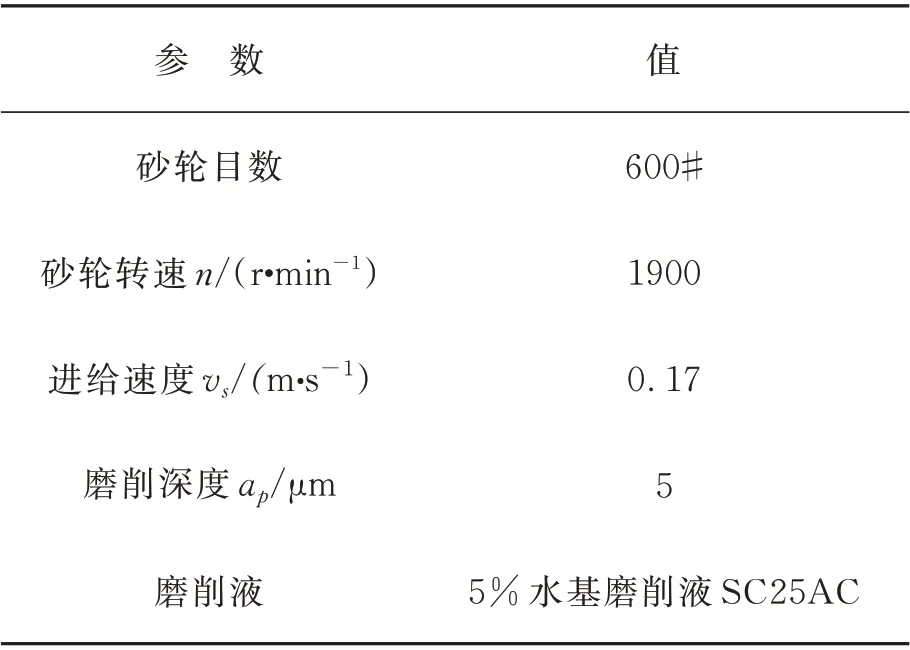
表4 磨削工艺参数Tab.4 Grinding experiment parameters

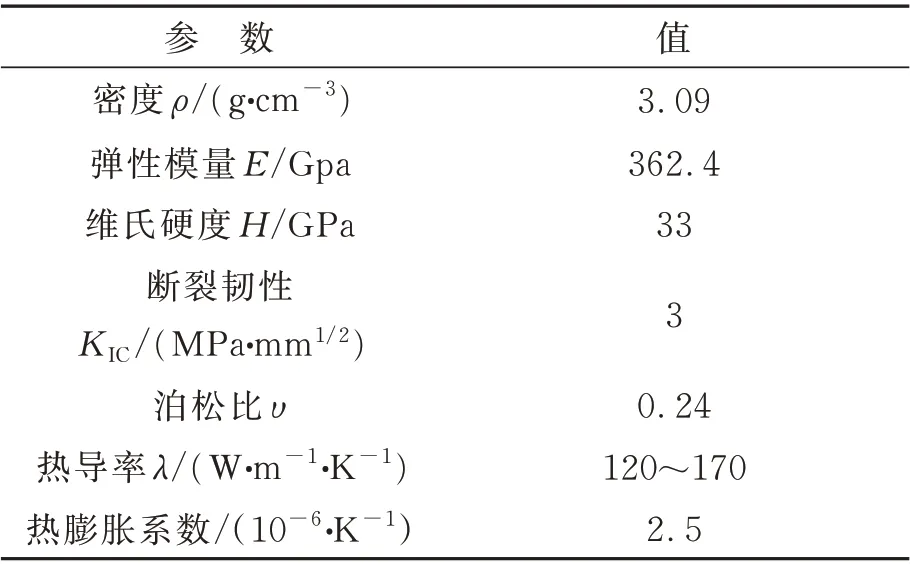
表5 RB-SiC 材料的机械性能参数［19］Tab.5 Mechanical properties of RB-SiC［19］

图15 磨削实验装置Fig.15 Grinding experiment equipment

4.2 仿真和实验结果分析

按照如上实验条件和磨削工艺参数分别进行磨削实验和仿真模拟，通过比较实验和仿真得到的磨削表面的面形误差和表面粗糙度验证仿真模型的正确性。图16 是磨削实验和仿真得到的工件的磨削表面形貌。从三维表面形貌图中可以看出，磨削实验和仿真模拟得到的表面有相同的纹理方向，都是沿着工件的进给方向，磨削实验的工件表面的纹理不如仿真的表面明显，原因是实际磨削加工中存在磨粒和工件接触区材料去除不完全的现象，并且在磨削过程中，当磨削深度超过脆塑转变临界切深时，材料发生脆性断裂［10，20-22］。如图16（a）所示，右上角的局部放大图可以看到磨削后的犁沟，但由于脆性断裂的破碎结构，犁沟结构不完整；从图16（a）右下角的同一区域的扫描电镜图中可以清楚地看到工件材料表面脆性断裂的破碎结构和纹理方向。

磨削实验和仿真的工件的截面形貌和理想截面形貌如图17 所示。图18 是磨削实验和仿真的工件面形误差的PV 值、粗糙度Ra和Rz值的对比。从图中可以看出，仿真工件和磨削实验工件的面形误差PV 值相差较小，这是因为工件的面形误差主要取决于复映的砂轮的轮廓误差。由于仿真时采用实测的砂轮轮廓，得到的仿真结果的面形误差和实际磨削加工的工件一致性较好。粗糙度无论是Ra值还是Rz值，磨削实验的工件都比仿真得到的工件大，同样是因为实际磨削加工中材料去除不完全，而且有一部分工件材料发生脆性断裂，如图16（a）所示。

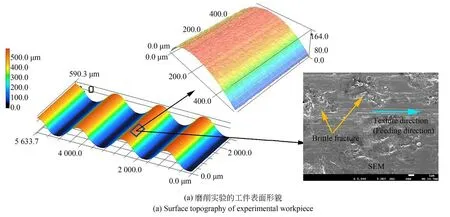
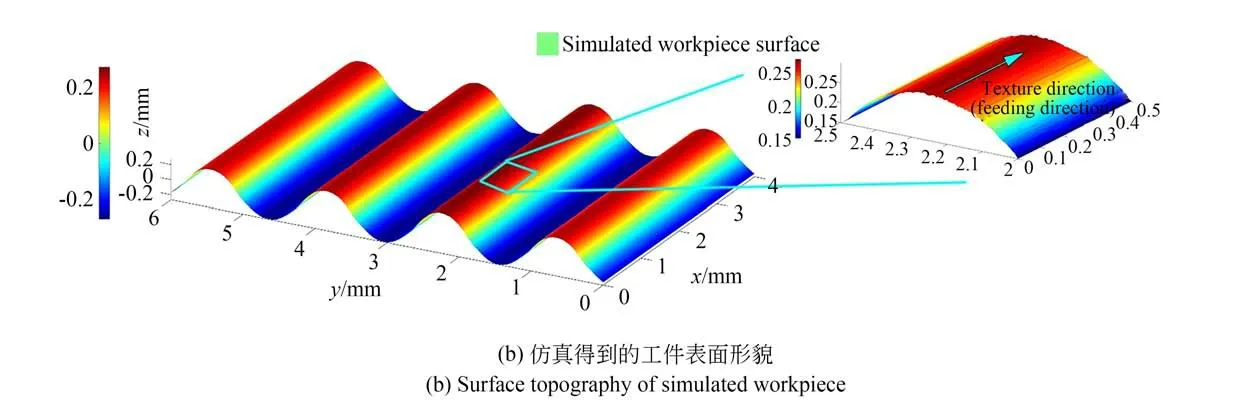
图16 实验及仿真结果Fig.16 Experimental and simulated results

图17 实验及仿真结果对比Fig.17 Comparison of experimental and simulated results

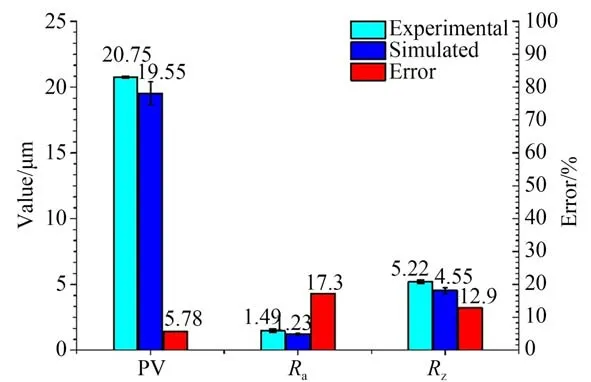
图18 磨削实验和仿真的工件面形误差的PV 值、粗糙度Ra和Rz值Fig.18 PV，Ra and Rz of surface errors of experimental and simulated workpieces

砂轮的跳动误差的影响主要体现在工件进给方向上的表面形貌。图19 是经过均值滤波处理后仿真的工件粗糙表面在x方向的曲线簇，从曲线簇中可以看到周期性波谷，这是由于砂轮存在周期性跳动误差。跳动误差为正最大处砂轮的磨削深度最大，相应的工件上被这部分砂轮磨削的区域形成x方向上的波谷，工件上被砂轮相邻跳动误差为正最大处磨削的区域的理论间距Lv为：

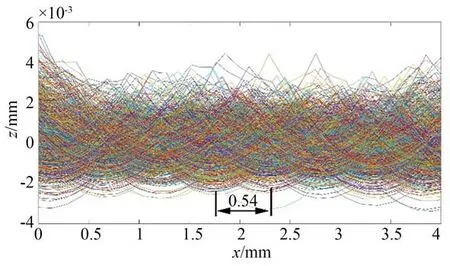
图19 均值滤波处理后仿真工件粗糙表面在x 方向的曲线簇Fig.19 Set of curves in x direction of simulated workpiece surface after average filtering

其中Ne是砂轮一周跳动误差的周期数，本文中为10。代入磨削参数计算得出Lv=0.537 mm。从图19 可以看到，相邻波谷之间的差值约为0.54 mm，和理论间距基本吻合。

5 结 论

本文采用频域分析法成功得到磨粒突出高度的偏态分布特征，并采用数字模拟法成功模拟了砂轮磨粒的突出高度分布特征，数学统计参数的误差在5%以内。基于实际的砂轮磨粒的突出高度分布、轮廓形貌和跳动误差，完成了空间砂轮的整体重构。建立了磨削运动学模型，成功仿真了工件的三维磨削表面。开展磨削实验验证了仿真模型的有效性，仿真预测与磨削实验的工件截面面形误差的PV 值偏差为5.78%。由于实际磨削加工中存在的材料去除不完全和脆性去除现象，仿真模型预测的磨削工件的表面粗糙度Ra和Rz都比磨削实验工件的小。由于砂轮存在跳动误差，工件表面在进给方向上会形成周期性的波谷，相邻波谷的间距Lv由砂轮一周跳动误差的周期数、砂轮转速和工件的进给速度决定。

本文提出了一种能够有效预测磨削表面面形精度和表面粗糙度的仿真方法。砂轮表面磨粒分布和轮廓均采用实测，因此该方法适用于不同粒度砂轮和不同形状微柱面的磨削加工，可用于研究砂轮粒度、轮廓形状和磨削工艺参数对磨削加工面形精度和表面质量的影响，针对超精密加工目标选择和优化砂轮与磨削参数，大幅提高加工效率。