基于幂律模型的橡胶沥青松弛模量预估

2021-09-01宋建军朱家剑韩丽丽

武汉理工大学学报（交通科学与工程版） 2021年4期

宋建军朱家剑韩丽丽傅琨

(甘肃省公路交通建设集团有限公司1) 兰州 730070) (甘肃路桥第三公路工程有限责任公司2) 兰州 730070)(陕西交通职业技术学院公路与铁道工程学院3) 西安 710018)(长安大学特殊地区公路工程重点试验室4) 西安 710064) (西安市公路勘察设计院5) 西安 710064)

0 引言

橡胶沥青是指由沥青、回收轮胎胶粉及外加剂组成的混合物.胶粉在高温发生融胀，吸收基质沥青的轻质组分，形成高黏度的热力学不相容两相体系.利用废旧轮胎回收胶粉生产橡胶沥青不仅能消化大量废弃轮胎，铺筑的路面还具有优良的高温抗变形、抗疲劳开裂性能和卓越的降噪效果.自从首次提出“湿法”工艺以来，就在中国、北美、南非、澳大利亚、比利时、法国、波兰及英国得到了广泛关注，被大量用于开级配、间断级配热拌沥青混合料，以及应力吸收层、同步碎石封层和开普封层等路面工程[1-3].

寒冷季节，沥青面层混合料因材料收缩而产生温度应力，当超过材料抗拉强度时便会产生横向裂缝，从而降低路面结构整体性，增加遭受水损害的风险.应力松弛能力是指对黏弹性材料施以恒定应变后，材料内部黏性应变分量随时间不断增长，总应力随时间逐渐衰减的能力.一般认为沥青混合料应力松弛能力愈强，混合料内部温度收缩应力随时间衰减得愈快，产生收缩裂缝的概率越低[4-6].沥青混合料的低温开裂性能主要取决于沥青的性质和用量，因此，沥青材料的应力松弛特性对评价沥青混合料低温抗裂性能至关重要.我国现行规范仍采用延度指标评价低温时橡胶沥青的抗裂性能，该方法经验性强，在理论依据、试验温度等方面存在局限.橡胶沥青属于黏弹性材料，基于黏弹性理论科学地表征其应力松弛特性对评价橡胶沥青低温抗裂性能具有重要意义.

本研究进行低温弯曲蠕变试验，测定了不同胶粉掺量橡胶沥青的弯曲蠕变劲度曲线，基于黏弹性力学模型进行参数拟合，预估得到不同橡胶沥青的应力松弛函数，以评价其低温应力松弛特性.

1 幂律(Power Law)模型及其黏弹性材料函数

流变学常采用各种模型表征材料的稳态剪切黏度与剪切速率、动态黏弹性参数与频率或时间之间的关系，主要有经典力学模型和数学模型两大类.前者利用基本力学元件(弹簧、黏壶)的组合来表达本构关系，依据组成模型力学元件的不同，有两元件模型、三元件模型、四元件模型等[7-8].在沥青材料流变性研究中被广泛应用的Burgers模型是由两个弹簧元件和两个黏壶组合成的四元件模型.数学模型代表性的有幂律模型，Sigmoidal模型等，是以特定的数学函数表达材料的流动规律.

幂律模型符合幂律分布，该模型形式简洁、参数少、对试验数据拟合效果好，因此被广泛地应用于沥青及聚合物材料流变性研究，还在物理学、计算机科学、生态学、人口统计学、金融学等众多领域得到广泛应用.

应力松弛和蠕变是表征材料静态黏弹性的两类重要试验[9-10].前者研究试样在恒定应变下应力随时间逐渐衰减的现象，试验结果为松弛曲线；后者研究对试样施加恒定应力后应变随时间增长的现象，试验结果为蠕变曲线.蠕变柔量函数是关于时间的单调递增函数，而松弛模量函数是关于时间的单调递减函数，若以幂律模型分别表征这两个材料函数，为

J(t)=J0tn

(1)

E(t)=E0t-m

(2)

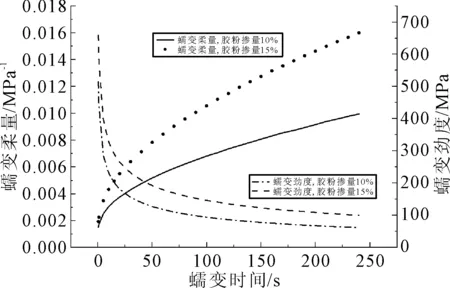
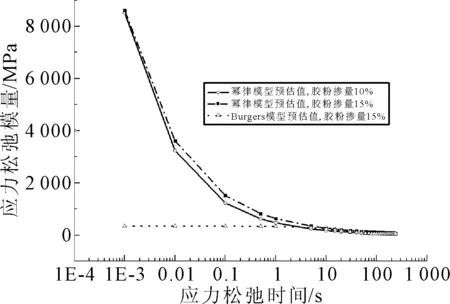
式中：J(t)为任意时刻t的蠕变柔量，Pa-1；J0为瞬态柔量，Pa-1；t为时间，s；E(t)为任意时刻t的松弛模量，Pa；E0为瞬态模量，Pa；m，n为幂律指数，m>0，0

黏弹性材料的松弛模量函数和蠕变柔量函数可以互相转换，从而实现一种试验模式下的材料特性向另一种模式下材料特性的转换，这对于获取受条件限制无法进行试验的流变参数具有重要意义.基于幂律模型，若已知材料的蠕变柔量函数J(t)，可通过Laplace变换得到其松弛模量函数，即

对式(1)取Laplace变换，得

(3)

式中：s为Laplace变换变量;Γ(n)为gamma函数.

由于蠕变柔量和松弛模量在Laplace像空间存在以下数学关系：

(4)

可得:

(5)

上式取Laplace逆变换，得松弛模量函数为

(6)

比较式(2)和式(6)，可得到以幂律模型表达的松弛模量函数的幂律指数、瞬时模量与蠕变柔量模型参数之间的关系：

(7)

由此可见，若试验测得材料的蠕变柔量曲线，用式(1)对蠕变曲线作非线性拟合，可得其幂律模型参数，根据幂律模型表达的松弛函数和蠕变函数模型参数之间的相互关系式(7)，可得其松弛函数表达式.

2 材料与试验方案

2.1 橡胶沥青

采用中海70#道路石油沥青作为基质沥青，在室内利用高速剪切工艺制备橡胶沥青.采用产自山东某化工厂的细度为380 μm胶粉，产品质量符合有关要求，两种胶粉掺量，分别为占基质沥青质量的10%和15%.为保证胶粉在基质沥青中充分溶胀，并获得均匀性良好的橡胶沥青试样，掺入胶粉后在190 ℃以不低于3 000 r/min高速剪切1 h.对所有橡胶沥青样本进行基本物理性质试验，结果见表1.

表1 橡胶沥青基本物理性质指标实测值

2.2 BBR试验

由于橡胶沥青低温时性质硬脆，施加应变较困难，因此本研究借助BBR弯曲蠕变试验测定橡胶沥青小梁的弯曲蠕变劲度，转换得到蠕变柔量曲线，并基于幂律模型预估得到应力松弛函数评价其低温应力松弛特性.

在试样未老化状态下测试，试验温度为-18 ℃，依据BBR弯曲流变仪测定的小梁试件跨中挠度，可得弯曲蠕变劲度为

(8)

式中：δ(t)为t时刻小梁跨中挠度，mm；P为施加的集中荷载，N；S(t)为材料的蠕变劲度模量,MPa；L为简支小梁的跨径，mm；b为梁宽，mm；h为梁高，mm.

由蠕变劲度知蠕变柔量为

(9)

3 橡胶沥青低温弯曲蠕变特性及其幂律模型参数

3.1 弯曲蠕变劲度及柔量曲线

BBR试验得到两组不同胶粉掺量的橡胶沥青低温蠕变劲度与蠕变柔量曲线见图1.

图1 不同胶粉掺量橡胶沥青-18 ℃蠕变曲线

由图1可知:胶粉掺量对橡胶沥青低温弯曲蠕变柔量、蠕变劲度影响较为显著.在温度相同的条件下，胶粉掺量越大，蠕变柔量越小，蠕变劲度模量越高.这主要是由于胶粉颗粒弹性较好，使橡胶沥青试样弹性变形比例提高，不可恢复变形比例降低，在恒定应力下产生永久变形较小.此外，图1还表明两组橡胶沥青蠕变柔量的差异随着蠕变的发展不断增大，由此可知，在实际工程应用中采用较高的胶粉掺量可适当降低橡胶沥青蠕变变形.

3.2 不同模型蠕变柔量拟合结果分析

基于黏弹性理论，利用式(1)的幂律模型的蠕变函数，对橡胶沥青样本BBR试验数据进行拟合，得到橡胶沥青样本的低温黏弹性参数，拟合结果见图2.此外，为了对比不同蠕变模型的拟合效果，图2还为目前沥青材料流变行为研究常用的Burgers模型的拟合结果.

图2 橡胶沥青-18 ℃蠕变柔量幂律模型拟合结果

由图2可知:随着蠕变时间增长，橡胶沥青蠕变柔量呈非线性增加的趋势，且幂律模型对橡胶沥青低温蠕变柔量的拟合效果很好.当试验温度为-18 ℃时，采用幂律指数0.419 4，瞬时蠕变柔量0.001 564 MPa-1的幂律模型，拟合度达到0.995 2，表明在橡胶沥青短期蠕变行为表征方面，幂律模型具有参数少、模型简单、拟合准确度高的优势.数据表明，胶粉掺量对幂律模型拟合结果有一定影响.掺量为10%时，幂律指数0.419 4，瞬时蠕变柔量0.001 564 MPa-1，掺量为15%时，幂律指数0.376 9，瞬时蠕变柔量0.001 227 MPa-1，说明胶粉掺量越大，幂律指数越小，瞬时蠕变柔量越小.

此外，图2还表明：在相同温度下，Burgers模型对蠕变柔量数据的拟合度不及幂律模型，拟合系数为0.926 7，尤其是在蠕变发展的后期，Burgers模型的拟合结果与试验结果差异逐渐增大，这说明Burgers模型仅适用于表征橡胶沥青的短期蠕变效应，对长期蠕变行为的表征则误差较大.

4 基于幂律模型的橡胶沥青低温松弛模量预估

研究表明:沥青的应力松弛特性与沥青混合料低温抗裂性能有密切联系，因此采用应力松弛模量评价橡胶沥青的低温路用性能更加合理[11].由于在较沥青下，应力松弛试验施加恒定应用较困难，松弛模量曲线不易测得.目前常采用BBR低温弯曲蠕变试验来评价沥青的低温抗开裂性能，故本研究基于BBR试验数据，依据黏弹性理论蠕变柔量和松弛模量的转换关系，根据幂律模型预估了橡胶沥青的应力松弛曲线，可用来评价其低温性能.

图3为胶粉掺量10%、15%的橡胶沥青样本在-18 ℃时的预估应力松弛曲线.由图3可知，胶粉掺量越大，瞬时松弛模量越大.-18 ℃时10%橡胶沥青瞬态松弛模量约为469.797 MPa，15%橡胶沥青瞬态松弛模量约为637.470 MPa，说明胶粉掺量越高，橡胶沥青弹性固体效应越显著.

图3 不同掺量橡胶沥青预估应力松弛曲线

当松弛10 s后，10%、15%的橡胶沥青样本松弛模量分别为178.859、267.645 MPa，表明胶粉掺量越大，应力松弛速度越慢.研究者常采用Burgers模型对沥青BBR蠕变行为进行表征[12]，故图中还给出了基于Burgers模型的预估应力松弛函数；由图3可知，在松弛发生的瞬间，该模型与幂律模型松弛预估结果相差较大，但在松弛后期，两种模型预估结果非常接近.一般认为，Burgers模型是一种线性黏弹性流体模型，用来表征沥青的高温蠕变特性效果较好[13-14]，而用于表征低温沥青的松弛效应则有一定的缺陷[15-16]，本研究表明幂律模型对橡胶沥青低温蠕变柔量拟合效果优于Burgers模型，进而基于幂律模型预估其应力松弛模量可靠性也优于Burgers模型.