基于分数阶自适应滑模的船舶非线性减摇控制

方琼林

集美大学 航海学院，福建 厦门 361021

1 引 言

船舶横摇是指以船舶重心所在的前、后轴线（纵轴线）为中心的回转摇晃，若幅度过大将严重影响船舶的适航性、适居性和安全性及其舰上设备的使用。此外，舰舶横摇还会对舰艇的战斗性能产生严重影响，若横摇角超过某一个限值时会带来船舶倾覆的危险。因此，安装船舶减摇装置是现代船舶设计的焦点之一，例如减摇水舱、舭龙骨和减摇鳍。目前，采用的减摇控制算法包括有神经网络控制、预测控制、H∞控制等。

20 世纪50 年代前，苏联学者提出了滑模控制(SMC) 方法，其是变结构控制的一个分支，属于非线性控制，通过切换函数来实现，根据系统状态偏离滑模的程度切换控制律或控制器参数。近年来，滑模控制方法在船舶运动领域得到了较快发展。例如，Lavieri 等[1]采用滑模技术来减小小型船舶的横摇运动；Moradi 等[2]针对船舶航行中影响减摇鳍系统的问题，采取了滑动模态控制；Ngo 等[3]为移动式港口起重机设计滑动面为期望的轨迹，针对滑模函数及其变化率，采用模糊逻辑调整滑模控制的增益抖动；Carletti 等[4-5]为减摇和航向保持问题设计了滑膜控制器，并介绍一种基于自适应神经网络的海洋机动艇鳍片横摇稳定滑模控制方法，采用径向基函数神经网络自适应学习系统的不确定性界，利用网络输出调整滑模控制增益；Fang 等[6]设计了一种由滑模控制器和视线导引技术，来研制自动驾驶仪系统；Koshkouei 等[7]设计了包括滚翼、滚舵和自动驾驶仪的船舶减摇滑模控制器；谢克峰[8]针对浮动平台的摇摆实验台设计了积分滑模控制器；王世凯等[9]运用滑模控制方法设计了同步横摇阻尼和航向保持控制器来调节一阶波浪扰动；梁利华等[10]为减摇鳍设计了切换模糊化非线性自适应滑模控制（ASMC）器；刘文帅[11]设计了滑模反演控制器，通过操控减摇鳍运动来抵消干扰；沈晓[12]设计了反步滑模自适应控制器，并将其应用于舵鳍联合减摇控制；胡建章等[13]充分考虑了不确定性干扰来设计欠驱动水面无人艇集群的自适应反步滑模控制器；刘志全等[14]提出带有航速损失约束的自动舵控制系统，依据舵角协同控制方法设计了航向和舵减摇滑模控制律。

然而，滑模变结构控制仍存在因为不连续开关特性所引起的系统抖振等问题。例如，当系统运动到滑模面且靠近平衡点时具有一定速度，在惯性等因素的影响下滑模面的两侧会出现反复运动，产生诸如抖振这样的负面效应。

诞生于1695 年的分数阶微积分（fractional order calculus）方法是一个重要的数学分支，其可处理扰动问题且控制性能良好，具有较快响应速度、较低超调量、更宽控制参数范围的特点。为此，赵蕊等[15]提出一种基于分数阶PID 技术的航向控制器，结合遗传算法完成了控制参数的自动整定，提高了控制器的实用性；Zhou 等[16]提出了一种基于深卷积神经网络的分数阶终端滑模控制策略，用于刚性机器人的跟踪控制，并采用深度学习方法对系统的不确定性进行补偿；Fei 等[17]提出的递归神经网络分数阶滑模控制方案结合了分数阶控制方法和递归神经网络结构；Modiri 等[18]采用具有分数阶滑动面的终端滑模控制器，对2 个具有参数不确定性和外部干扰的分数阶混沌系统状态进行了同步；Han[19]将分数阶滑模面与分数阶非线性扰动观测器结合，提出一种基于分数阶指令滤波器的反推控制方法，引入基于分数阶的命令滤波器。

鉴于分数阶自适应滑模控制(FOASMC)算法已在其他领域获得应用，但在国内外尚未有将分数阶自适应滑模控制算法应用到船舶横摇减摇领域的相关文献报道，本文拟在减摇滑模控制中引入分数阶算法，以便更好地降低横摇角的均值和标准差，获得更佳的减摇控制效果，从而进一步克服模型不确定性和外界环境扰动所导致的系统不确定性。

2 船舶非线性横摇运动模型

本文以船舶质心为原点Ob，船舶前进方向为xb轴 ，横荡方向为yb轴，垂荡方向为zb轴，建立船体的坐标系。如图1 所示。图中， φ为船舶横摇角。

图1 船舶横摇模型Fig. 1 Ship rolling model

船舶非线性横摇运动模型为[20]

3 分数阶自适应滑模控制

3.1 分数阶微积分

Caputo 形式的分数阶微积分定义如下[21-22]：

3.2 分数阶自适应滑模控制

式中，c为控制律增益，且满足下式：

3.3 稳定性分析

定理：基于Lyapunov 稳定性理论，考虑船舶非线性横摇系统运动学方程式(4)和基于分数阶自适应滑模控制器式(8) 及自适应控制律式(9)，则系统的横摇角跟踪误差将渐进稳定。

为了防止造成抖振，采用如下饱和函数代替符号函数。

式中： Δ为边界层参数； s at(h) 为h的饱和函数，其中h为任意实数。

4 实例与分析

4.1 实例介绍

为验证基于分数阶自适应滑模控制的算法在船舶横摇中的控制效果，采用表1 所示主要参数[1]。

表1 船模参数Table 1 Parameters of ship model

4.2 闭环横摇控制与比较

实验测试采用Intel(R) Core(TM) i3-4150T CPU@ 3.00 GHz、内存4.00 GB 的64 位操作系统、基于x64 的处理器完成。图2 为船速v=10 m/s、不同遭遇浪向角（μe）下海浪的Pierson-Moscowitz (PM)谱曲线，图3 为遭遇浪向角70°时不同船速下海浪的P-M 谱曲线。

图2 不同遭遇浪向角下海浪P-M 谱（v=10 m/s）Fig. 2 P-M spectrum of waves in different directions at v=10 m/s

图3 不同船速下海浪P-M 谱（ μe=70°）Fig. 3 P-M spectrum of waves at different ship speeds when μe=70°

图4 为船速5 m/s、遭遇浪向角60°时开环控制与闭环控制时的横摇角曲线。

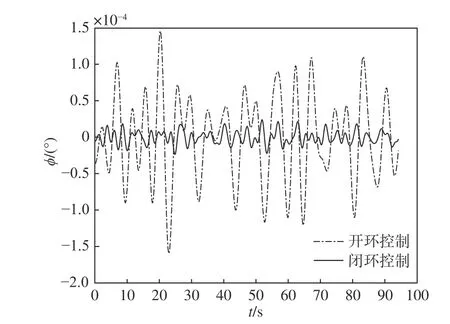
图4 开环控制与闭环控制时的横摇角曲线Fig. 4 Rolling angle curve of open-loop control and closed-loop control

参数设置如下： α=0.9,c=0.16,λ=1。图5 为船速5 m/s、遭遇浪向角80°时的横摇角滑模闭环控制曲线, 图6 为船速5 m/s、遭遇浪向角90°时的横摇角滑模闭环控制曲线，图7 为船速5 m/s、遭遇浪向角100°时的横摇角滑模闭环控制曲线。

图5 横摇角滑模闭环控制曲线（v=5 m/s， μe=80°）Fig. 5 Sliding mode closed loop control curve of rolling angle (v=5 m/s， μe=80°)

图6 横摇角滑模闭环控制曲线（v=5 m/s， μe=90°）Fig. 6 Sliding mode closed loop control curve of rolling angle (v=5 m/s， μe=90°)

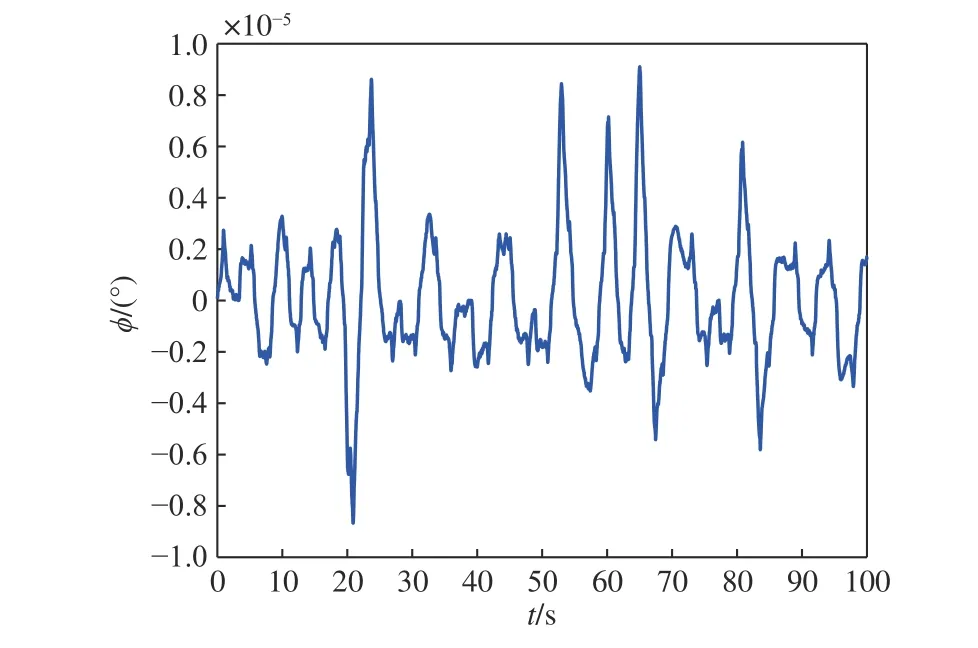
图7 横摇角滑模闭环控制曲线（v=5 m/s， μe=100°）Fig. 7 Sliding mode closed loop control curve of rolling angle (v=5 m/s， μe=100°)

图8 为船速10 m/s、遭遇浪向角80°时的横摇角滑模闭环控制曲线，图9 为船速10 m/s、遭遇浪向角90°时的横摇角滑模闭环控制曲线，图10 为船速10 m/s、遭遇浪向角100°时的横摇角滑模闭环控制曲线。

图8 横摇角滑模闭环控制曲线（v=10 m/s， μe=80°）Fig. 8 Sliding mode closed loop control curve of rolling angle (v=10 m/s， μe=80°)

图9 横摇角滑模闭环控制曲线（v=10 m/s， μe=90°）Fig. 9 Sliding mode closed loop control curve of rolling angle (v=10 m/s， μe=90°)

图10 横摇角滑模闭环控制曲线（v=10 m/s， μe=100°）Fig. 10 Sliding mode closed loop control curve of rolling angle (v=10 m/s， μe=100°)

图11 为本文所提分数阶自适应滑模控制算法与基本滑模控制算法、自适应滑模控制算法计算结果的比较。

图12 为本文所提分数阶自适应滑模控制算法与基本滑模控制算法控制输入的比较。由图可见，本算法能减少控制输入的抖振现象。

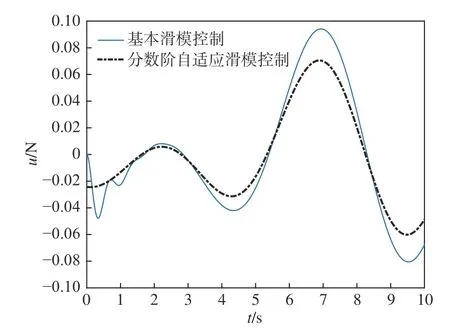
图12 不同控制算法的控制输入比较Fig. 12 Input comparison of of different control algorithms

图13 所示为系统相空间控制曲线。由图可见，系统被控后稳定在原点，相空间的轨迹是收缩的，逐渐趋近于原点，运动稳定，且对初始条件不敏感。

图13 系统相空间控制曲线（v=5 m/s， μe= 120°）Fig. 13 System phase space control curve (v=5 m/s， μe= 120°)

综合以上各图可以看出，对于不同的船速、遭遇浪向角等情况，分数阶自适应滑模控制均有更好的减摇控制效果。

为了验证本文所提算法的有效性，将本文所提算法与基本滑模控制算法进行了比较。表2 给出了不同船速和遭遇浪向角下控制系统横摇角的均 值 和 标 准 差。参 数 设 置 如 下：c=1， α=0.5，λ=1。表中数据均为计算20 次后的平均值，具有统计意义。其中，EFOASMC和 σFOASMC表示用分数阶自适应滑模控制算法计算的横摇角均值和方差，ESMC和 σSMC表示用基本滑模控制算法计算的横摇角均值和方差，EOpen和 σOpen表示用开环控制算法计算的横摇角均值和方差。

表2 不同算法计算结果比较Table 2 Result comparison of different control algorithms

由以上结果的比较可见，与基本滑模控制算法相比，在相同实例和运行条件下，分数阶自适应滑模控制算法得到的横摇角均值和标准差更小，控制效果更好，减摇控制结果令人满意。

4.3 参数影响分析

为了了解各个主要参数对算法计算性能的影响，分别对分数阶、控制律增益、滑模面增益等参数取不同的数值，分别比较其对控制效果的影响。

4.3.1 分数阶的影响分析

对4.3 节所述运动情况，取c=1，λ =1，v=5 m/s，μe=90°，其他参数不变。不同分数阶微分阶数计算的横摇角均值和方差如表3 所示。

由表3 可见：当分数阶微分的阶数较小时，横摇角均值较小，即系统稳态误差较小；当分数阶积分的阶数较大时，横摇角标准差较小，即系统波动较小，与稳定期望值的偏离程度较小。

表3 不同分数阶阶数计算的结果比较Table 3 Result comparison of fractional orders

基于分数阶滑模控制能使系统收敛。不同分数阶下调节过程的性能有异，故可根据实际情况，选取不同分数阶微积分算子，使系统满足不同的动态和静态，控制效果更好。因整数阶微分是特例，整数阶积分是分数阶微积分的特例，故整数阶微积分是分数阶微积分的特例。分数阶微积分参数选择范围更大、更灵活。

4.3.2 控制律增益影响分析

对 于4.3 节 所 述 运 动 情 况，取 α=0.5， λ=1，v=5 m/s， μe=90°，其他参数不变，不同控制律增益c情况下船舶横摇角的均值和方差值见表4。

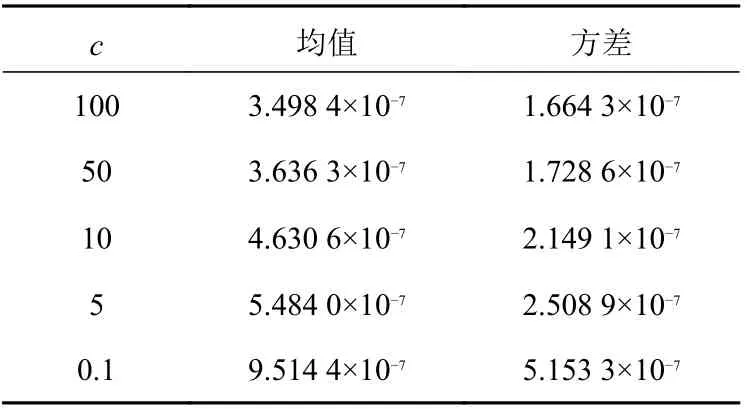
表4 不同控制律增益的计算结果比较Table 4 Result comparison of control law gains

由表4 可见：当c值较大时，横摇角均值较小（系统稳态误差较小）且横摇角标准差较小（系统波动较小），与稳定期望值的偏离程度较小。

4.3.3 滑模面增益影响分析

对4.3 节所述运动情况，取 α=0.5，c=1，v=5 m/s， μe=90°，其他参数不变，不同滑模面增益λ 情况下的船舶横摇角的均值和方差值见表5。

表5 不同滑模面增益计算的结果比较Table 5 Result comparison of sliding mode surface gains

由表5 可见：当λ 的值较小时，船舶横摇角均值较小，即系统稳态误差较小；而且横摇角标准差较小，即系统波动较小，与稳定期望值的偏离程度较小。

5 结 语

本文针对船舶非线性横摇运动控制问题，提出了一种分数阶自适应滑模控制算法，证明了闭环系统的稳定性。对分数阶微积分的阶数、控制率增益和滑模面增益系数进行了比较，分析其对控制效果的影响。实验结果证明，新算法在不同船速、遭遇浪向角的情况下，相对于基本滑模控制算法都有更好的减摇控制效果。与基本滑模控制算法相比，在相同的实例和运行条件下，分数阶自适应滑模控制的横摇角均值和标准差更小，控制效果更好。例如，当船速10 m/s、遭遇浪向角5°时，本文控制算法控制的横摇角均值是基本滑模控制的25.89%，均方差是基本滑模控制的14.32%，减摇控制结果令人满意。当分数阶微分的阶数较小时，横摇角均值较小，即系统稳态误差较小； 当分数阶积分的阶数较大时，横摇角标准差较小，即系统波动较小，与稳定期望值的偏离程度较小； 控制率增益较大时，船舶横摇角均值较小（即系统稳态误差较小）且横摇角标准差也较小（即系统波动较小），与稳定期望值的偏离程度较小； 当滑模面增益较小时，船舶横摇角均值较小（即系统稳态误差较小）且横摇角标准差也较小，即系统波动较小，与稳定期望值的偏离程度较小。

下一步将继续改进本控制算法，以进一步提高非线性横摇运动的控制精度和鲁棒性能。