“单位名称”教学：意义理解是正道

刘艳

摘要：学生计算解决实际问题时单位名称出错的情况屡见不鲜，究其原因，主要在于学生对四则运算相关意义的理解存在偏差。对此，从量词含义、数量关系、算理、算法等四个维度提出获得意义理解的几种做法。

关键词：单位;量词;数量关系;算理;算法

在一节《表内乘、除法》复习课上，教师设计了一道蚂蚁喝豆浆问题，学生核对答案时出现了图1所示的算式正确、单位名称出错的情况。经统计，班上有近20%的学生解决这道题时在单位名称上出现了错误。最后的单位究竟是“杯”还是“只”，一部分学生分不清楚。

有教师将此类错误归结为学生的粗心，只反复和学生强调答题时要细心;也有教师要求学生圈画出问题中“多少”“几”等后面的字，让学生机械地从问句中找单位名称，导致对于“妈妈一共用去多少钱”的问题，学生出现“10（钱）”这样的错误。其实，单位名称出错的主要原因在于学生对四则运算相关意义的理解存在偏差。

事实上，与单位名称有关的四则运算意义主要有四个：量词含义、数量关系、算理、算法。规范表达、数形结合、操作体验、说清步骤就是获得意义理解的几种做法。

一、训练规范表达，理解量词含义

虽然苏教版小学数学教材从一年级上册《20以内的进位加法》单元开始示范写单位名称，从一年级下册“求被减数的简单实际问题”开始要求学生在得数后面标上单位并进行相应的口答，但在实际教学中，从学生入学起就应该训练规范的量词表达。例如，教学一年级第一节课《数一数》时，笔者引导学生规范使用量词表达物体的数量，如“4架小飞机、5只蝴蝶、8棵大树、10个小朋友”等。再如，教学《认识1—5》一课时，笔者引导学生在“1个男孩、1架手风琴、1块黑板”等丰富的素材中抽象出数字符号“1”，并說说“1”还可以表示什么，于交流中规范量词的使用与表达。

二、利用数形结合，理解数量关系

“数缺形时少直观。”数量关系获得几何解释，可以使问题变得直观易懂，使人易于洞察问题的本质。因此，教师要引导学生善用数形结合解决问题，将抽象的数学语言与直观的图形结合起来，将数量之间的关系以图的形式表达出来。例如，教学“周期问题”时，笔者让学生结合分一分、圈一圈的过程，画出示意图（如图2），并结合图说一说算式中每个数的具体含义——虽然商与余数都是3，但从图中能清楚地看出，商3表示圈了3组，余数3表示剩余3个，表示的意义不同，单位名称自然也不同。

三、结合操作体验，理解算理

算理，顾名思义，就是运算过程中的道理，解决“为什么这样算”的问题。小学生以具体形象思维为主，不太容易理解抽象的算理，需要经历动手操作等具身认知过程。例如，对于“认识除法”，教材安排先认识平均分，再认识除法，将平均分的过程与除法算式及含义建立充分的联系。但学生实际解决问题时，只知道平均分用除法计算，对平均分的过程却不细加思考，导致单位名称出错。针对这样的情况，在进行平均分的教学时，笔者让学生结合分小棒操作，明晰平均分的过程和方法，知道分的是什么，怎么分的，分的结果是什么。然后，结合平均分的具体情境，教学除法算式的写法和含义，使学生不仅体会到除法是解决平均分问题的一种运算方法，还认识到被除数是要分的总数，除数是平均分的份数或每份数，商是平均分的结果。真正将除法算式与平均分的过程建立联系，将平均分的过程与算式中的每个数对应起来，从而深刻理解算理。

四、说清解题步骤，理解算法

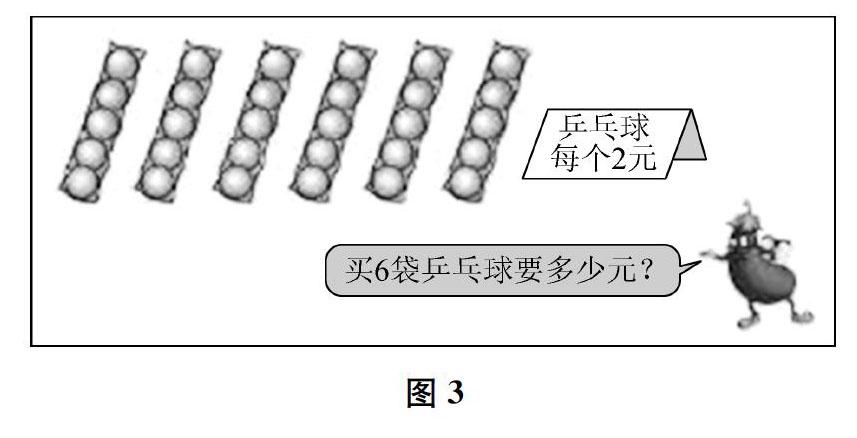
两步或三步计算的实际问题，涉及的量较多，单位名称不尽相同。有时一道题目往往不只有一种解法，解题思路不同，每一步的单位名称也可能会不同。因此，说清楚每一步求的是什么就显得尤为重要。例如，教学“两步连乘实际问题”（如图3）时，学生出现了三种算法：（1）2×5=10，10×6=60;（2）5×6=30，30×2=60;（3）2×6=12，12×5=60。方法（1）先求1袋乒乓球多少元，方法（2）先求一共有多少个乒乓球，因此第一步的单位名称不同，一个是“元”，一个是“个”。有学生因为感觉解决这个问题需要把三个数乘起来，故萌生了方法（3），但对第一步的单位名称却犹豫不定。这时，结合情境图，笔者引导学生发现，“2×6”求的是“如果每袋有1个乒乓球，一共要多少元”，即“一‘行乒乓球12元”，从而确定单位是“元”。学生在三种算法的阐述与说理中明确解题思路，找准单位名称;同时，单位名称的确定也佐证了学生的思路，启发学生多角度思考问题，理解不同的解题方法。

参考文献：

[1] 曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，2006.

[2] 史宁中.基本概念与运算法则——小学数学教学中的核心问题[M].北京：高等教育出版社，2013.

[3] 吴正宪，刘劲苓，刘克臣.小学数学教学基本概念解读[M].北京：教育科学出版社，2014.