小学数学教学中的思辨能力培养

吴佳佳

摘要：思辨能力就是思考、辨析的能力，问题的引领则是思辨能力生长的重要动力。在小学数学课堂中，可以通过循序渐进的设问、“大问题”统领的追问、多角度的“质问”，着力培养学生的思辨能力。

关键词：思辨能力;小学数学;设问;追问;“质问”

思辨能力就是思考、辨析的能力，思考指的是推理、判断等思维活动，辨析指的是对事物的情况、类别、道理等的辨别分析。“问题是数学的心脏。”在小学数学课堂中，可以通过循序渐进的设问、“大问题”统领的追问、多角度的“质问”，着力培养学生的思辨能力。

一、于循序渐进的设问中培养

数学教学应该是促进学生思考、启发学生智慧的过程。教师要对教学有全局的把握，通过循序渐进的设问，引导学生不断地思考、辨析，唤醒思辨意识，培养思辨能力。

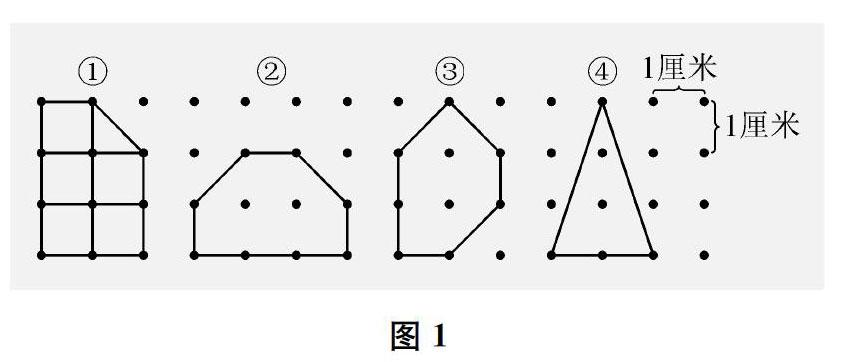
例如，教学《钉子板上的多边形》一课时，教师设置了如下问题：

1.如图1所示，请大家观察这些多边形，它们的内部都有2个钉子，那它们有什么不同呢？

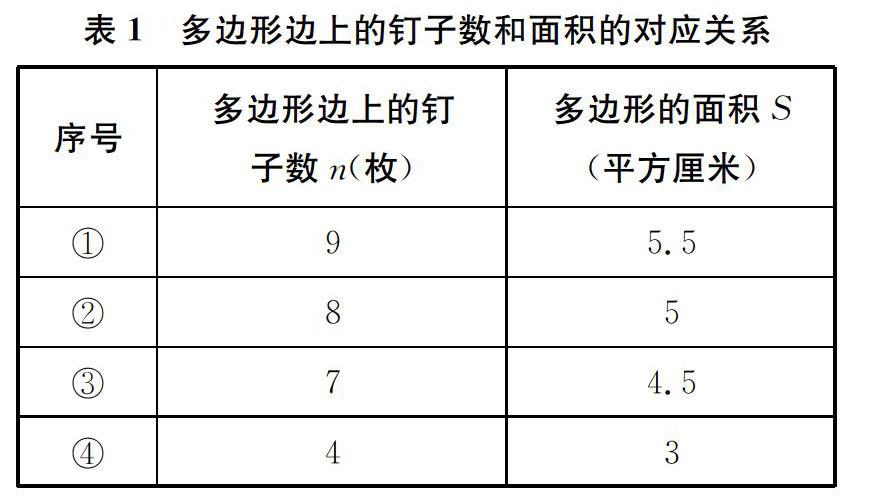
2.观察表1中的数据，多边形的面积和边上的钉子数之间有没有关系？有怎样的关系呢？

（平方厘米）①95.5②85③74.5④433.内部钉子数是2的多边形的例子举得完吗？我们能不能找到一个反例，证明这个规律不存在呢？

这里，教师没有直接出示表格，而是通过提问先让学生聚焦特征，思考发现规律的第一步要做什么，辨析哪些特征可能会和规律有关，把看似不相干的数字联系起来;接着，再让学生思考、探索，明白规律的发现、观点的得出是需要证据来支撑的;在探索出规律后，继续让学生寻找反例，促使学生在强化思考过程严密性的同时充分认识规律的外延，持续地思辨。

二、于“大问题”统领的追问中培养

思辨能力的一个重要表现是，能进行有逻辑、有条理的思考，进而做到层次分明、条理清楚的分析。“大问题”统领的追问对学生这一表现的达成有很好的推进作用。

例如，教学《整数除以分数》一课时，教师在“整数除以分数怎么算？”这个“大问题”的统领下，有层次地追问“为什么”“怎么验证”“还有什么”，指引学生经历思辨的过程：

教师出示“4÷25”，指名学生口算，根据学生回答课件呈现：4÷25=4×52=10。教师追问：同意吗？反思一下，为什么这么做？学生回答：因为25÷4=25×14，所以4÷25=4×52。教师追问：能举例子来验证这样的算法吗？学生用画图的方法举例：小明25小时走了4千米，他平均每小时走多少千米？如图2所示，4÷25=4÷2×5=10（千米）。教师追问：还有其他方法吗？学生交流：（1）4÷25=4÷0.4=10;（2）4÷25=205÷25=10;（3）4÷25=4×5÷25×5=10。

整数除以分数的算法，学生很容易掌握，而对于为什么这样算（算理），学生则“心求通而未达，口欲言而未能”。于是，教师通过“大问题”统领的追问，不断引导学生沟通算法之间的联系。在层级递升的追问中，学生不但加深了对知识点的理解，还经历了充实的思辨过程，培养了思辨能力。

三、于多角度的“质问”中培养

这里的“质问”指质疑地问，是指建立在良好的判断之上，用合理的、开放的方式对别人或自己已有的观点、方法进行辨析。通过多角度的“质问”，学生能综合不同维度、向度的思考得出结论，获得数学知识本质的透彻理解，走向深刻思辨。

例如，教学《认识小数》一课时，教师设置了如下问题：

1.我们刚刚测量了两个长方形的长和宽（如图3、图4所示），都用分米作单位时，为什么第一个长方形的长和宽可以用整数来表示，第二个长方形的长和宽却要用分数来表示？

2.既然可以用厘米表示，为什么要用分数呢？既然有了分数，为什么还要有小数呢？

3.既然叫“小数”，它一定很小吗？

为什么用分数表示？既然有了分数，为什么还要引入小数？这些问题引导的是学生对小数价值的探寻，即与分数相比，小数有什么特别之处。小数一定很小吗？这一问题引导学生完善对小数的认识——小数包含整数部分和小数部分，整数部分大的话，小数也就大。将来还有可能认识什么样的数呢？这是学生自发生成的“质问”，是他们自主思辨意识的体现，表明了他们思辨能力的发展。

参考文献：

[1] 陈士文.“智慧數学”之数学改造[M].南京：江苏凤凰教育出版社，2016.

[2] 胡彩云.《钉子板上的多边形》教学设计及思考[J].小学教学设计，2019（32）.