内置式多层磁钢永磁同步电机振动噪声抑制措施
2021-08-28韩雪岩张新刚朱龙飞马鑫王世伟
韩雪岩,张新刚,朱龙飞,马鑫,王世伟
(沈阳工业大学 国家稀土永磁电机工程技术研究中心,沈阳110870)
0 引 言
噪声是三大公害之一,由强度与规律都不相同的声音无规律的组合产生,影响人们的身心健康。电机的噪声根据产生的原理不同可将其分为三类,即电磁噪声、机械噪声和通风噪声。其中电磁噪声是电机主要的噪声源[1]。当电机的通风噪声较低时,其电磁噪声更加突出,并且电磁噪声是导致电机负载时噪声增大的根本原因[2-3]。因此,研究电机的设计参数与电磁噪声的关系对在电机设计阶段预估和抑制电机的振动噪声有着重要的意义。
如何抑制电机的电磁噪声是国内外学者研究的热点问题之一。电机中的径向电磁力作用于定子铁心使电机定子及机壳发生周期性振动从而引起周围空气脉动发声,是电机产生电磁噪声的主要原因[4-5]。对电机的径向电磁力阶次进行分析发现低阶电磁力对电机的振动噪声影响最大[6]。对比分析不同极槽配合电机的径向电磁力阶次发现,8极12槽电机的最低力波阶次高于10极12槽电机,因此在电机振动噪声的抑制上,8极12槽电机与10极12槽电机相比更具优势[7]。分析电机径向电磁力的产生原理,发现可通过降低电机的气隙磁密波形畸变率,降低径向电磁力幅值抑制电机的振动噪声。经过研究发现可通过选择合适的极弧系数降低电机的声压级。进一步分析发现电机的磁极偏心距离影响径向电磁力幅值,因此可通过选择合适的磁极偏心距离降低降电机的电磁噪声[8-9]。对电机的转子结构进行分析发现,可在电机转子外侧开辅助槽,通过辅助槽降低电机气隙磁密波形畸变率,抑制电机的电磁噪声[10]。也可通过优化内置式永磁同步电机转子中磁钢形状和位置的4项参数实现在不降低电机平均转矩的情况下降低电机振动幅值的目的[11]。还可通过优化电机转子结构,以增大电机磁阻,进而降低径向电磁力密度,抑制电机的振动噪声[12]。对电机的定子结构进行分析发现,可对电机定子齿边形状进行曲线化设计,进而通过有限元参数化仿真进行优化,从而最大程度降低电机空载和负载时的径向电磁力幅值,实现降低电机声压级的目的[13]。
内置式多层磁钢永磁同步电机与普通永磁同步电机相比转子内磁钢层数更多,电机凸极率更高,磁阻转矩在电磁转矩中的占比更大。因此与普通永磁同步电机相比可减少磁钢用量,节约电机成本。但随着电机凸极率的增加电机的振动噪声问题同样较为突出,而目前国内对内置式多层磁钢永磁同步电机振动噪声的问题研究较少。为此,本文通过基于直接耦合场的有限元仿真方法,针对内置式多层磁钢永磁同步电机的转子结构,研究不同磁钢层数对电机振动噪声的影响。进而提出磁钢槽端部削角与转子侧开隔磁孔两种优化方法对电机转子结构进行优化,降低电机的声压级。并通过推导不同极槽配合的永磁同步电机的主要电磁力阶次,分析极槽配合对电机振动噪声的影响,实现在电机设计阶段预估和抑制电机振动噪声的目的。
1 基于直接耦合场的永磁同步电机振动噪声仿真验证
永磁同步电机的径向气隙磁密和切向气隙磁密可分别表示为:
br=bxcosθ+bysinθ;
(1)
bt=bycosθ-bxsinθ。
(2)
进而由麦克斯韦张量法求得电机气隙中单位面积的径向电磁力可表示为[14]
(3)
由于电机的切向气隙磁密远远小于径向气隙磁密,因此忽略切向气隙磁密,将电机的径向电磁力表示为
(4)
对一台额定功率20 kW,基准频率300 Hz的内置式永磁同步电机建模仿真,电机定转子1/8仿真模型如图1所示。电机主要参数如表1所示。

表1 永磁同步电机主要参数Table 1 Main parameters of permanent magnet synchronous motor
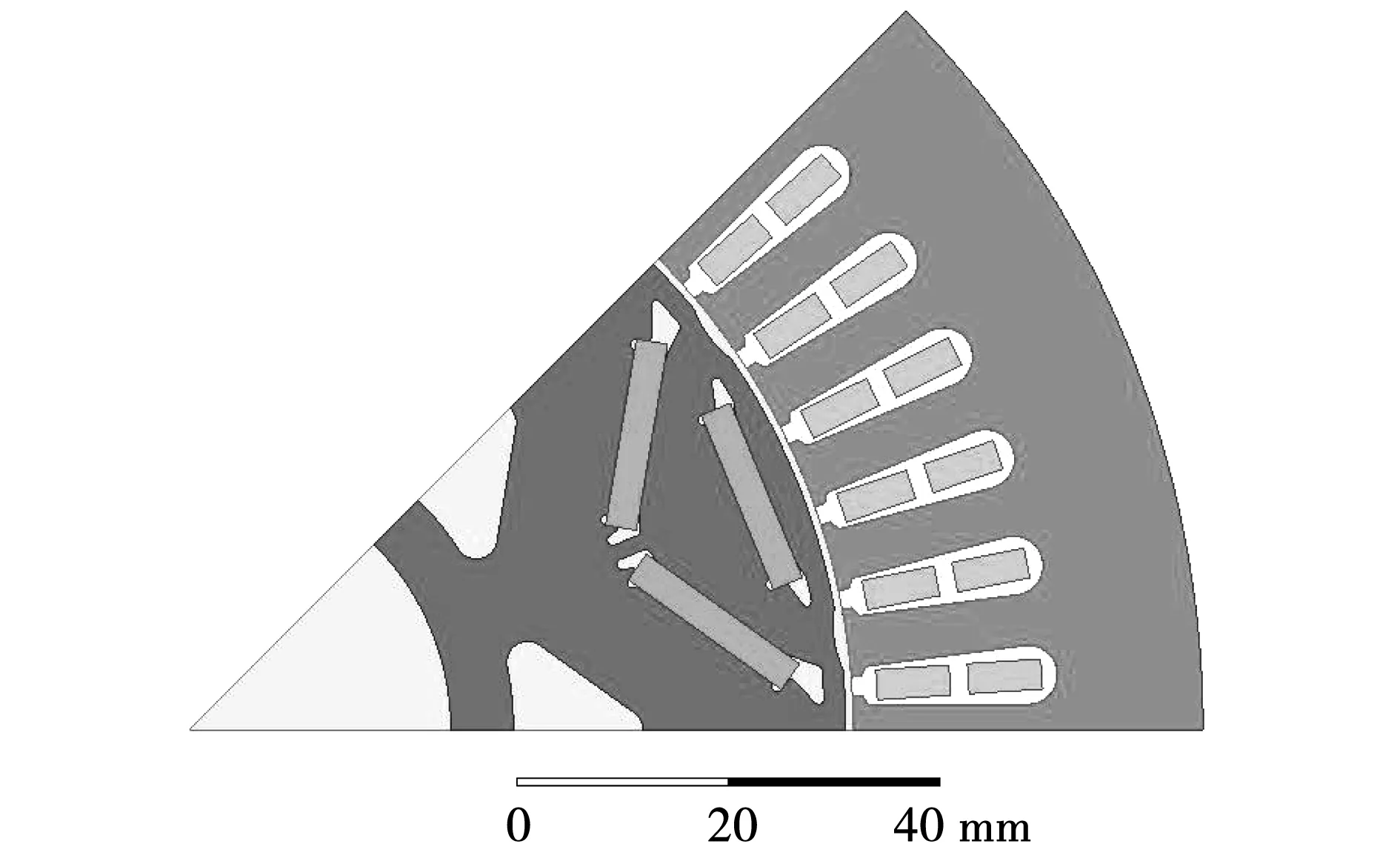
图1 电机定转子仿真模型Fig.1 Simulation model of fixed rotor of motor
通过式(4)可求得电机气隙中单位面积下的径向电磁力。由于电机的径向电磁力包含空间分量和时间分量,因此对其进行空间与时间的二维傅里叶分解,其结果如图2所示。

图2 径向电磁力二维傅里叶分解Fig.2 Two-dimensional fourier decomposition of the radial electromagnetic force
从图2中可看出该台电机的径向电磁力空间阶次主要为0阶、8阶与16阶。由于高阶径向电磁力并不是引起电机振动噪声的主要因素,并且0倍基频的电磁力也不会引起电机的振动噪声[15]。因此对比除去0倍基频后的0阶电磁力,电磁力频谱如图3所示。
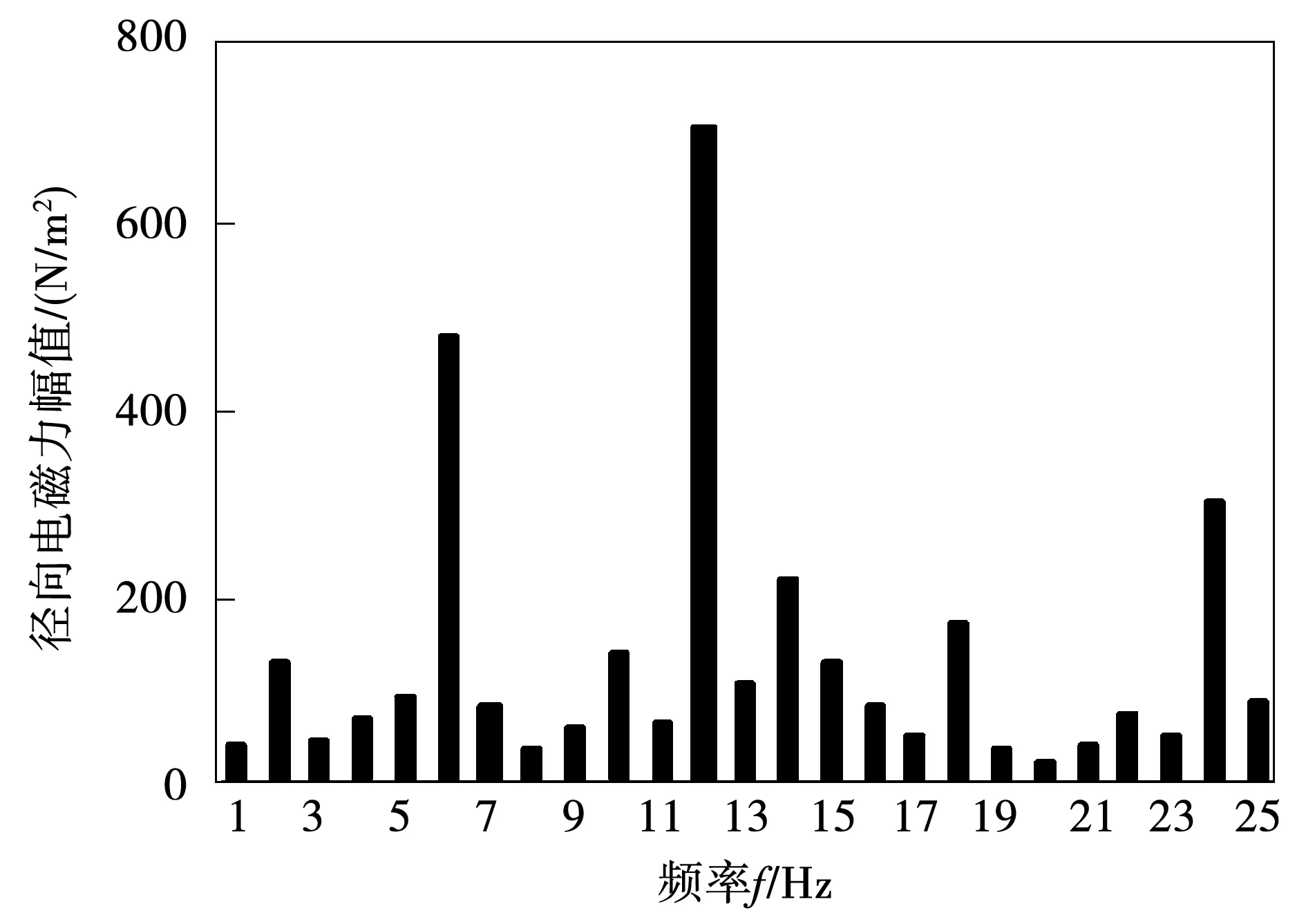
图3 除去0倍基频后的0阶电磁力频谱Fig.3 0-order electromagnetic spectrum with 0 fundamental frequency removed
从图中可看出,该台电机除去0倍基频后的0阶电磁力在6倍基频、12倍基频与24倍基频处力波幅值最大。进一步将电机电磁力导入谐响应分析模块,对电机的振动噪声进行仿真计算。仿真求得电机机壳上某点处的声压级频谱如图4所示。

图4 电机声压级频谱Fig.4 Frequency spectrum of motor sound pressure Level
在消声室对该台电机进行半球法噪声实验,计算电机在不同转速下的声压级。将电机噪声实验测得的声压级与有限元仿真计算所求得的值进行对比,如表2所示。
由于电机噪声实验所测得的噪声中不可避免的包含了机械噪声,而仿真计算只求得了电机的电磁噪声,因此仿真值与实验值并不完全一致。从表2中可看出样机声压级的仿真值与实验值较为接近,其最大差值低于6.3%,因此可验证仿真计算电机振动噪声方法的准确性。由于多层磁钢永磁同步电机在振动噪声仿真计算方法上与样机完全一致,因此可采用有限元仿真方法计算内置式多层磁钢永磁同步电机的振动噪声。

表2 样机噪声实验值与仿真值对比Table 2 Comparison of experimental and simulated noise values of prototype
2 转子结构对内置式多层磁钢永磁同步电机振动噪声的影响
内置式多层磁钢永磁同步电机可产生高凸极率,增加电机磁阻转矩在电磁转矩中的占比。因此与普通内置式永磁同步电机相比,在输出相同转矩时磁钢用量更少。采用与样机相同的极槽配合且保持电机定子结构不变,但转子改为常用的U型磁钢的转子结构,通过该转子结构分析不同磁钢层数对电机振动噪声的影响。进而对电机的转子结构提出优化措施,抑制电机的振动噪声。
2.1 磁钢层数对电机振动噪声的影响
在气隙磁密幅值近似相等的情况下仿真分析磁钢层数为1至4层时电机的声压级。2层磁钢与3层磁钢电机的转子结构如图5所示。对不同磁钢层数的电机进行仿真分析,求得电机除去0倍基频后的0阶电磁力频谱对比如图6所示。

图5 不同磁钢层数电机转子结构Fig.5 Rotor structure of motor with different number of permanent magnet layers
从图6可看出,当电机采用多层U型磁钢的转子结构时,0阶电磁力幅值依然集中在6倍基频、12倍基频和24倍基频处。进一步对不同磁钢层数电机的振动噪声进行仿真分析。为更直观表明不同磁钢层数对电机振动噪声的影响,以4层磁钢电机的声压级为对照值,其他磁钢层数电机的声压级与其差值用差值百分比的形式表示。仿真得到不同磁钢层数电机的声压级对比如表3所示。从表中可看出,当电机采用3层或2层磁钢的转子结构时声压级较低。尤其2层磁钢电机与4层磁钢电机相比声压级降低了6.9%,在抑制电机振动噪声上优势明显。因此,在设计多层磁钢电机时将磁钢层数设计为3层或2层对抑制电机的振动噪声较为有利。
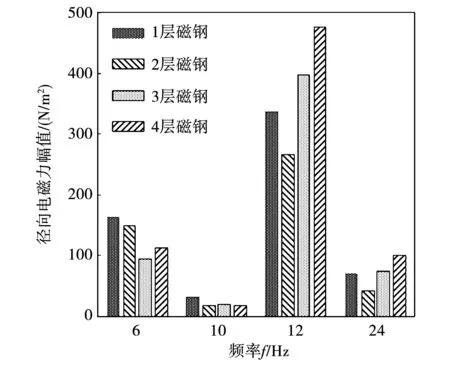
图6 不同磁钢层数电机0阶电磁力频谱对比Fig.6 Spectrum comparison of 0-order electromagnetic force of motors with different number of permanent magnet layers
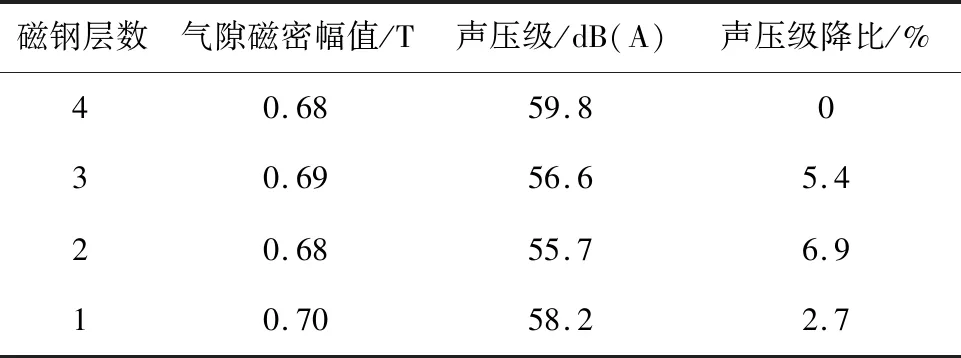
表3 不同磁钢层数电机声压级对比Table 3 Comparison of motor sound pressure levels with different magnet layers
2.2 磁钢槽端部削角抑制电机的振动噪声
当内置式多层磁钢的永磁同步电机采用3层磁钢的转子结构时,磁钢产生的磁通大部分通过相邻两层磁钢槽端部中间的转子部分进入气隙,在该区域较易形成磁路饱和,增加气隙磁密的谐波含量。当电机气隙磁密中3、5次谐波含量增多时尤其易增加电机的振动噪声。针对此种现象,可通过对磁钢槽端部进行削角处理,增大磁通路径,减小磁路饱和程度,从而降低电机的声压级。通过有限元仿真不同削角位置和削角角度发现,若对电机磁钢槽端部削角过大,则在降低电机声压级的同时也会增加电机的漏磁系数,对电机的电磁性能产生影响。若对电机磁钢槽端部削角过小则无法起到增大磁通路径,减小磁路饱和程度的目的。因此需通过有限元参数化仿真分析最优削角位置和削角角度,实现在不影响电机电磁性能的前提下降低电机的声压级。以上文中3层磁钢永磁同步电机的转子结构为例,通过有限元参数化仿真对磁钢槽端部进行削角处理,确定了最优削角措施,磁钢槽端部削角前后电机转子结构对比如图7所示。
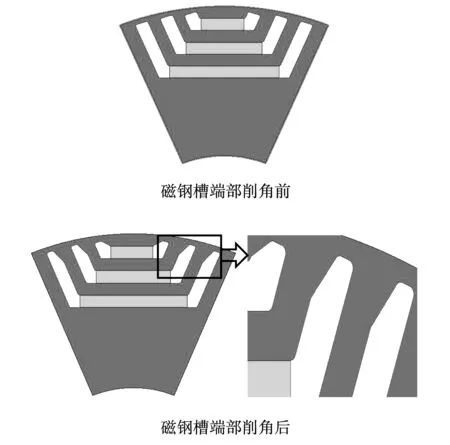
图7 磁钢槽端部削角前后电机转子结构对比Fig.7 Comparison of motor rotor structure before and after permanent magnet slot end corner cutting
对磁钢槽端部削角前后的电机进行仿真分析,电机径向气隙磁密谐波幅值对比如图8所示,电机除去0倍基频后的0阶电磁力频谱对比如图9所示。
从图8中可看出在对磁钢槽端部削角处理后,电机径向气隙磁密除11次与15次谐波幅值略有增加外其余次数谐波幅值均有所降低,尤其是3次谐波幅值降比达73.8%。从图9中的0阶电磁力频谱对比可看出对磁钢槽端部的削角处理降低了电机的径向电磁力幅值,尤其是12倍基频处的力波幅值降低了32.5%,这对抑制电机的振动噪声十分有利。进一步对磁钢槽端部削角前后电机的声压级进行仿真分析,其声压级对比如表4所示。从表中可看出对磁钢槽端部进行削角处理后电机的声压级降低了8.1%,表明该优化方法可有效抑制电机的振动噪声。因此对内置式3层磁钢的永磁同步电机可通过对磁钢槽端部进行削角处理抑制电机的振动噪声。

图8 磁钢槽端部削角前后电机径向气隙磁密谐波幅值对比Fig.8 Comparison of radial air gap flux density harmonic amplitude of the motor before and after permanent magnet slot end corner cutting

图9 磁钢槽端部削角前后电机0阶电磁力频谱对比Fig.9 Spectrum comparison of 0-order electromagnetic force of the motor before and after permanent magnet slot end corner cutting

表4 磁钢槽端部削角前后电机声压级对比Table 4 Comparison of motor sound pressure levels before and after magnetic barrier end corner cutting
2.3 转子开隔磁孔抑制电机的振动噪声
当内置式多层磁钢的永磁同步电机采用2层磁钢的转子结构时可在转子侧开对称的隔磁孔,通过隔磁孔改变电机磁路走向,优化气隙磁密波形,降低波形畸变率,抑制电机的振动噪声。通过有限元仿真发现,若转子侧所开的隔磁孔宽度过大会降低电机q轴电感,使电机凸极率降低,输出转矩减小。若所开隔磁孔宽度过小则无法起到改变磁路走向,优化气隙磁密波形的目的。因此通过有限元参数化仿真分析不同隔磁孔宽度及夹角对电机振动噪声的抑制效果和对电机电磁性能的影响,实现在不影响电机电磁性能的前提下降低电机的声压级。以上文中2层磁钢的转子结构为例,通过有限元参数化仿真确定了最优开孔措施,开隔磁孔前后电机的转子结构对比如图10所示。

图10 开隔磁孔前后电机转子结构对比Fig.10 Comparison of motor rotor structure before and after magnetic isolation holes slotting
对开隔磁孔前后的电机进行仿真分析,电机径向气隙磁密的谐波幅值对比如图11所示,电机除去0倍基频后的0阶电磁力频谱对比如图12所示。
从图11中可看出,对电机转子侧开隔磁孔后,电机径向气隙磁密除15次谐波幅值略有增加外其余次数谐波幅值均有所降低,其中3次谐波幅值降低25%,5次谐波幅值降低46.1%。从图12中可看出,当电机径向气隙磁密谐波幅值降低后,使得电机0阶电磁力在各倍基频处的力波幅值均有所降低,其中6倍基频处力波幅值降低36.8%,12倍基频处力波幅值降低23.2%,与开隔磁孔前相比明显削弱了电机的径向电磁力幅值。进一步对开隔磁孔前后电机的振动噪声进行仿真分析,其声压级对比如表5所示。从表中可看出,对电机开隔磁孔后其声压级降低了5.9%,证明该优化方法可有效抑制电机振动噪声。因此,2层磁钢的内置式永磁同步电机可通过对电机转子侧开对称的隔磁孔抑制电机的振动噪声。

图11 开隔磁孔前后电机径向气隙磁密谐波幅值对比Fig.11 Comparison of radial air gap flux density harmonic amplitude of the motor before and after magnetic isolation holes slotting

图12 开隔磁孔前后电机0阶电磁力频谱对比Fig.12 Spectrum comparison of 0-order electromagnetic force of the motor before and after magnetic isolation holes slotting

表5 开隔磁孔前后电机声压级对比Table 5 Comparison of motor sound pressure levels before and after magnetic isolation holes slotting
3 极槽配合对永磁同步电机振动噪声的影响
永磁同步电机的极槽配合影响电机径向气隙磁密的谐波含量并决定电机电磁力阶次。同时,电机槽数的改变会影响定子各阶模态的固有频率。当电机定子模态的固有频率与相应阶次电磁力的时间频率较为接近时会产生共振,对电机的振动噪声产生影响[16]。由于电机的电磁力幅值近似与其阶次的4次方成反比,因此,电磁力阶次越低对电机的振动噪声影响越大。推导8极9槽、8极12槽、8极36槽和8极48槽4种常用极槽配合的永磁同步电机的电磁力阶次,分析其对电机噪声值的影响。永磁同步电机的每极每相槽数可表示为
(5)
式中:Z为定子槽数;m为电机相数;P为电机极对数。
当q为整数时,电机的定子磁场谐波次数可表示为[17]
v1=(6k1+1)p。
(6)
当q为分数时,将式(5)化为最简分数的形式,可表示为
(7)
式中t为单元电机数。
若d为偶数,则电机定子谐波磁场次数与转子谐波磁场次数可分别表示为[18]:
(8)
(9)
若d为奇数,则电机定子谐波磁场次数与转子谐波磁场次数可分别表示为:
(10)
μ2=(6k1+1)dt。
(11)
式中:k1=±1,±2,±3,…;k2=0,1,2,3,…。
为突出对比不同极槽配合的永磁同步电机的电磁力阶次,对上述4种极槽配合的电机取小于等于8阶的电磁力进行分析,不同极槽配合电机的主要电磁力阶次如表6~表9所示。
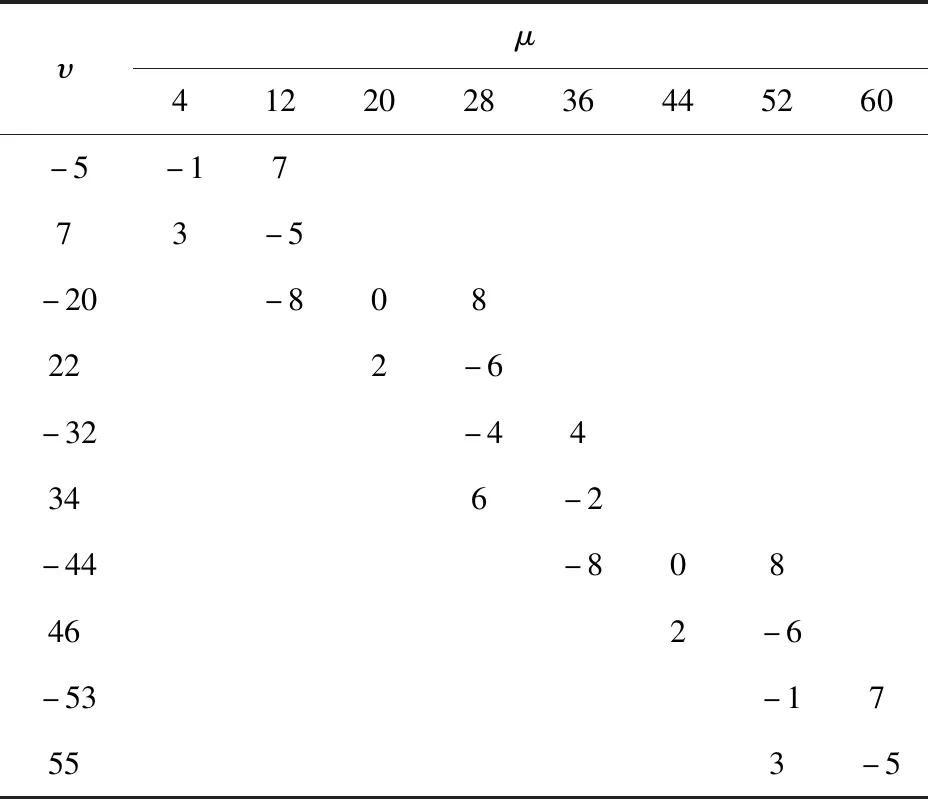
表6 8极9槽电机主要电磁力阶次Table 6 Main electromagnetic force orders of 8-pole 9-slot motor

表7 8极12槽电机主要电磁力阶次Table 7 Main electromagnetic force orders of 8-pole 12-slot motor

表8 8极36槽电机主要电磁力阶次Table 8 Main electromagnetic force orders of 8-pole 36-slot motor
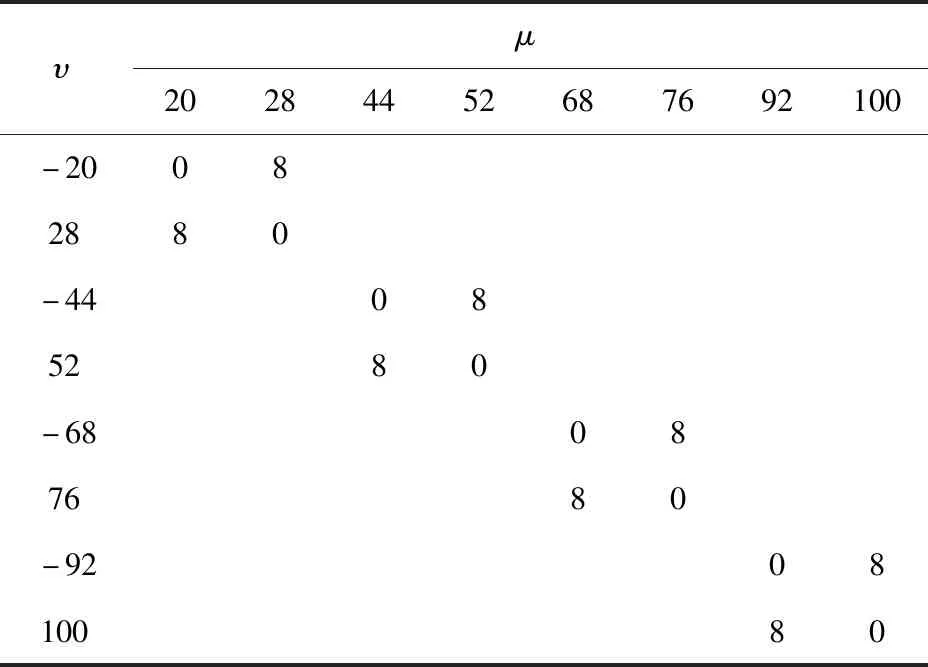
表9 8极48槽电机主要电磁力阶次Table 9 Main electromagnetic force orders of 8-pole 48-slot motor
从表6~表9中可看出,8极9槽电机除0阶电磁力外最低力波阶次为1阶,8极12槽与8极36槽电机除0阶电磁力外最低力波阶次为4阶,而8极48槽电机除0阶电磁力外最低力波阶次为8阶。由于8极48槽电机为整数槽电机,电磁力阶次只能为0或2P的整数倍,由此避免了低阶电磁力对电机振动噪声的影响。因此,在上述4种极槽配合中8极48槽的极槽配合在抑制电机振动噪声上具有优势。对4种极槽配合的电机进行建模仿真,径向气隙磁密谐波幅值对比如图13所示。定子各阶模态固有频率对比如表10所示。进一步计算不同极槽配合电机在额定转速下的声压级,为更直观表明不同极槽配合对电机振动噪声的影响,以8极9槽电机的声压级为对照值,其他极槽配合电机的声压级与其差值用差值百分比的形式表示。不同极槽配合电机的声压级对比如表11所示。
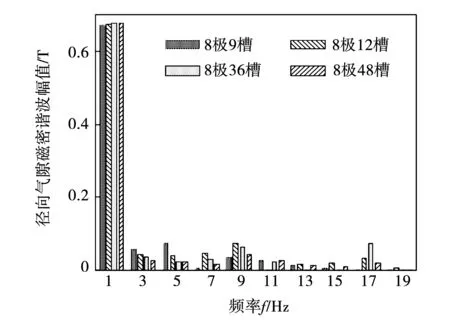
图13 不同极槽配合电机径向气隙磁密谐波幅值对比Fig.13 Comparison of radial air gap flux density harmonic amplitude of the motor with different polar slots
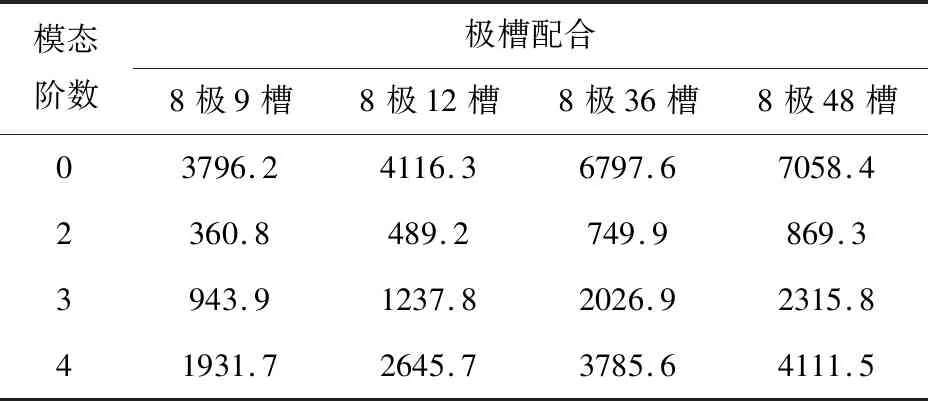
表10 不同极槽配合电机定子各阶模态固有频率对比Table 10 Natural frequency comparison of each mode of motor stator with different pole slots
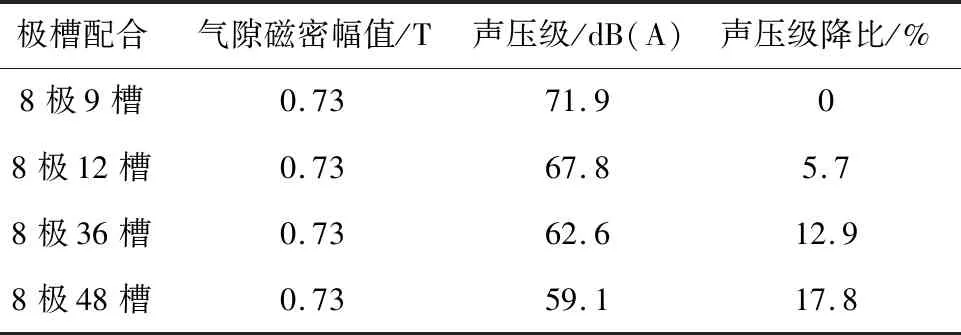
表11 不同极槽配合电机声压级对比Table 11 Comparison of sound pressure levels of motors with different pole slots
从表11中可看出,极槽配合对电机振动噪声的影响十分明显。8极48槽电机的声压级与8极9槽相比降低了17.8%,因此选择合适的极槽配合可有效抑制电机的振动噪声。其中整数槽电机声压级明显低于其他3种极槽配合的分数槽电机,验证了整数槽的极槽配合在抑制电机振动噪声上的优势。从表10中可以看出,随着电机定子槽数的增加,定子各阶模态固有频率也随之增加。当电机的模态阶次与电磁力的阶次一致,且相同阶次的频率也较为接近时才会产生共振。因此,对8极48槽电机来说只需关注0阶模态固有频率,8极12槽与8极36槽电机除0阶模态固有频率外,还需关注4阶模态固有频率,而8极9槽电机则需关注5阶模态以下的各阶模态固有频率。仿真分析表明,上述4种极槽配合电机的各阶模态固有频率与相应阶次电磁力的时间频率并不接近,因此并不会产生共振,对电机振动噪声的影响有限。进一步对比发现8极12槽与8极36槽电机虽然电磁力阶次相同,但8极36槽电机声压级与8极12槽电机相比降低了7.2%,证明与8极12槽相比8极36槽的极槽配合对抑制电机的振动噪声更为有利。从图13中可看出,8极36槽电机径向气隙磁密除11次谐波外其余次数谐波幅值均低于8极12槽电机,其中3次谐波幅值降低了17.3%,5次谐波幅值降低了43.1%。这是由于8极36槽电机每极下的槽数更多,降低了定子齿谐波对电机振动噪声的影响。因此在两种不同极槽配合电机的电磁力阶次相同时,每极下槽数更多的极槽配合可以更好降低电机的声压级。
4 结 论
本文通过基于直接耦合场的有限元仿真方法计算一台额定功率为20 kW的电机的振动噪声。电机声压级仿真值与实验值的差值小于6.3%,验证了本文仿真计算电机振动噪声方法的准确性。
针对内置式多层磁钢永磁同步电机的转子结构进行分析,得出在电机设计时将磁钢层数设计为3层或2层对抑制电机的振动噪声较为有利。进一步提出对3层磁钢电机可通过在磁钢槽端部进行削角处理,对2层磁钢电机可通过在转子侧开对称的隔磁孔,以降低电机的声压级。优化后电机的声压级较优化前分别降低了8.1%和5.9%,有效抑制了电机的振动噪声。
通过对比分析4种常用极槽配合的永磁同步电机的声压级,验证了整数槽的极槽配合在抑制电机振动噪声上优势明显。进一步通过对比4种极槽配合电机定子各阶模态的固有频率发现8极48槽的整数槽电机与其他3种极槽配合的分数槽电机相比发生共振的可能性更低。并且当在两种不同极槽配合电机的电磁力阶次相同时,每极下槽数更多的极槽配合可以更好的抑制电机振动噪声。
