基于SAE与改进LightGBM算法的笼型异步电机故障诊断方法
2021-08-28许伯强何俊驰孙丽玲
许伯强,何俊驰,孙丽玲
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引 言
笼型异步电动机广泛应用于电气传动领域。异步电机故障频发,据统计全国每年异步电机维修费用达20亿元[1],电机故障诊断对提高生产率、降低成本具有重要意义。电机故障在线监测可以避免停机检修带来的经济损失[2]。
由于在制造和安装过程中定子绕组的绝缘破损,加之工作环境与机械、电磁等原因导致振动、摩擦而损伤绝缘,笼型异步电动机在运行过程中可能发生定子绕组匝间短路故障;由于转子导条受到径向电磁力、旋转电磁力、离心力、热弯曲挠度力等交变应力的作用,加之转子制造缺陷,因而笼型异步电动机在运行过程中可能发生转子断条故障。
文献[3]指出电机故障种类比例如表1所示。

表1 笼型异步电机故障占比Table 1 Fault proportion of asynchronous motor
定子绕组匝间短路和转子断条均是典型的渐进性故障,因此,进行定子绕组匝间短路以及转子断条故障诊断具有重要意义。
笼型异步电动机定子某相绕组发生匝间短路故障后,三相平衡关系遭到破坏,负序分量变化明显,同时三相阻抗角以及定子电流的某些频率分量也会产生一定的变化。因此,定子绕组匝间短路故障的典型特征为负序阻抗,当前的定子绕组匝间短路故障诊断方法也大多依赖于此单一故障特征[3-5]。实际上,除负序阻抗以外,负序电压和故障相电流的幅值也是受定子绕组匝间短路故障影响较大的量,如果将这些量按照一定的权重占比加以综合而诊断故障,将比传统的依赖于单一故障特征的诊断方法更加可靠。
笼型异步电动机发生转子断条故障之后,定子电流中将出现(1±2s)f1频率的边频分量(s为转差率,f1为供电频率),这是典型的转子断条故障特征。而定子电流信号易于采集,因此基于傅里叶变换的定子电流信号频谱分析方法被广泛应用于转子断条故障诊断。为了改进故障诊断的性能,自适应滤波、派克变换、希尔伯特变换以及高频率分辨力谱估计技术[7-8]被引入该领域而形成了一系列的笼型异步电动机转子断条故障诊断方法。但是这些方法在本质上均是传统的依赖于单一故障特征的诊断方法,其性能仍有待提高。且对定子转子故障联合诊断时,故障特征的提取难度增大,难以准确辨别定子故障。
更重要的是,由于定、转子之间的双边电磁感应关系,笼型异步电动机的定子绕组匝间短路和转子断条故障相互影响,其故障特征也存在一定程度的相互交织。因此,孤立的定子绕组匝间短路故障诊断或孤立的转子断条故障诊断往往混淆这两种故障而做出错误诊断。
本文提出一种基于深度学习与梯度提升决策树模型相结合的故障诊断方法,能够自动提取异步电机定子绕组匝间短路和转子断条故障的特征,并准确对故障多分类,从而实现定子绕组匝间短路和转子断条故障及其严重程度的联合、同时诊断。
1 栈式自编码器
普通自编码器是一种结构为三层,且输入输出层神经元数目相同的神经网络;降噪自编码器是对实验数据进行加噪处理,利用降噪编码实现数据降噪[10];栈式自编码器类似一种堆叠的深层自编码器,它使用逐层贪婪训练法依次训练每层网络,确保每个层损失最小化[11]。
1.1 生成数据集
在训练之前对输入数据进行构建。数据集制作过程如下:首先对采样数据进行快速傅里叶变换,直接从每个样本中提取到20个故障特征(A相电压幅值、B相电压幅值、C相电压幅值、A相电流幅值、B相电流幅值、C相电流幅值、A相电压相位、B相电压相位、C相电压相位、A相电流相位、B相电流相位、C相电流相位、正序电压有效值、负序电压有效值、正序电流有效值、负序电流有效值、正序阻抗模值、负序阻抗模值、定子电流(1+2s)f1边频分量、定子电流(1-2s)f1边频分量),得到每种负载27 002个样本数据,共81 006个样本,构成输入数据{X}。
标签对应故障种类和严重程度,标号0~6分别对应正常、定子绕组匝间短路故障(轻微)、定子绕组匝间短路故障(中等)、定子绕组匝间短路故障(严重)、转子断条故障(轻微)、转子断条故障(中等)、转子断条故障(严重)7种状态,形成标签数据集{Y}。
1.2 模型训练


图1 降噪自编码器原理Figu.1 Main theory of denoising auto encoder
构建编码器和解码器。编码器结构为3层(输入层、中间层、输出层),每层神经元数量依次递减(20、16、8),如图2。
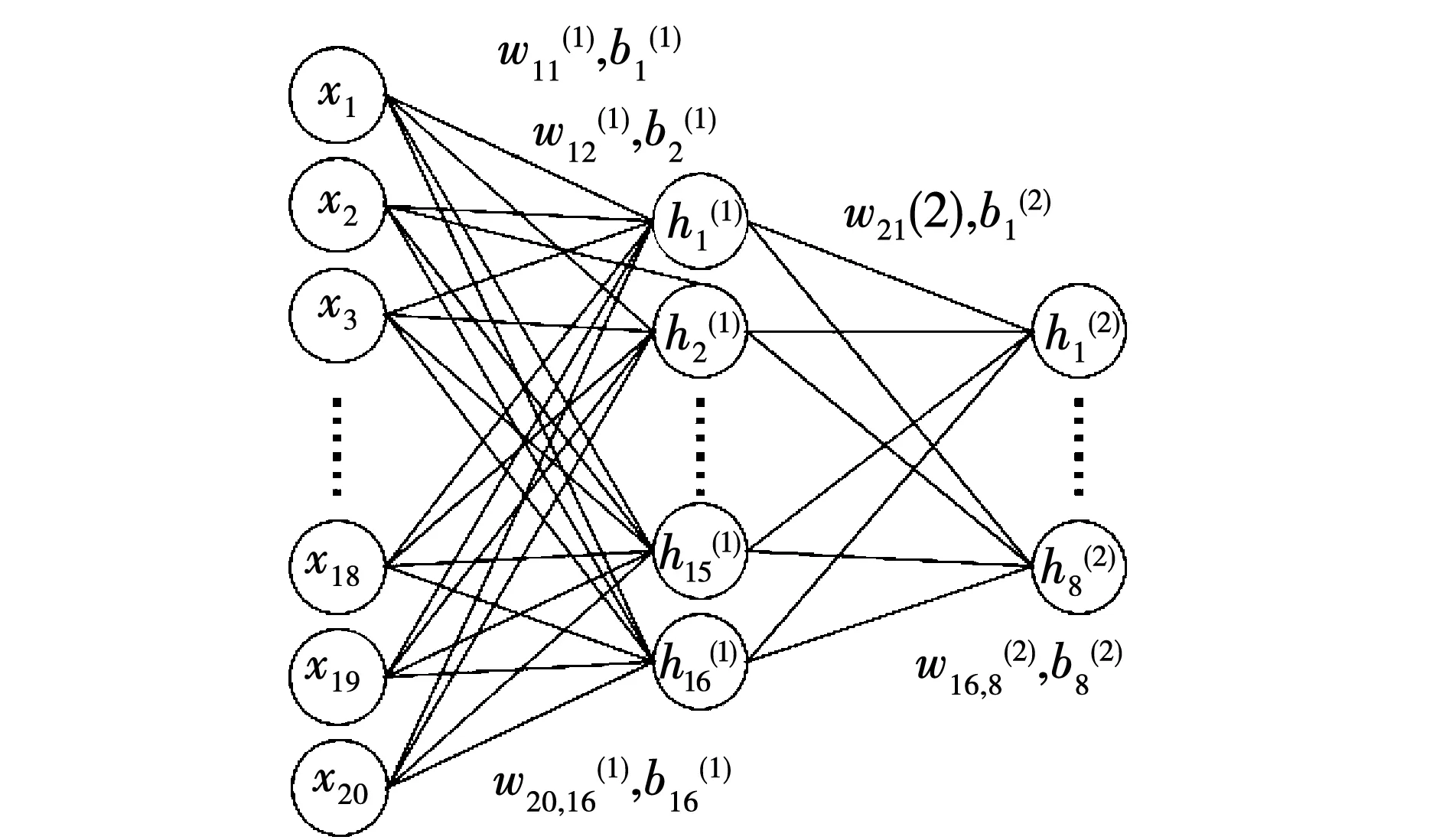
图2 编码器结构Fig.2 Structure of encoder
图中输入层至中间层的关系、中间层至输出层神经元的关系分别如下:
(1)
X′=sigmoid(W(2)H+b(2))。
(2)
其中:W(1)为输入层至中间层神经元的dmid×din维的权重矩阵;W(2)为中间层至输出层神经元的dout×dmid维的权重矩阵;b(1)为输入层至中间层神经元的维度为dmid的偏置矩阵;b(2)为中间层至输出层神经元的维度为dout的偏置矩阵;din=20为输入样本数据的维度,即编码器输入层数据的维度;dmid=16为编码器中间层数据的维度;dout=8为编码器输出层数据的维度;sigmoid为激活函数,用于激活神经元的输出,使神经元非线性化。
式(1)、式(2)组成编码映射为
(3)
解码器结构与编码器对称,即包含3层(输入层、中间层、输出层),每层神经元数量逐层递增(8、16、20),整个流程与编码器相反[13],此处不做详细介绍。
在进行训练前对权重和偏置进行随机赋值,然后对每个原始输入数据与解码后的重构数据计算重构误差,即
(4)
损失函数选用MSE均方误差函数;全部样本的重构误差均值和正则项相加得到成本函数,即
(5)

前述为正向传播过程,反向传播(backward propagation,BP)过程利用随机梯度下降算法计算梯度值,并更新权重和偏置,即
(6)
其中α为学习率,经实验最优值为0.005。
正向传播计算成本函数,反向传播更新权重和偏置矩阵来优化成本函数,两者组成迭代循环,本文经过300次迭代,成本函数达到最小值,对编码器输出层(即编码数据)进行保存,形成81006×8的二维编码数据集{X′}。
2 改进LightGBM算法
轻型梯度提升机是梯度提升决策树的一种优化算法,其优化方向为损失函数负梯度方向[21];GBDT不仅引入集成学习,还在训练过程中,下一轮训练在本轮训练结果叠加残差的基础上继续拟合,因此每一轮拟合曲线都是上一轮拟合曲线和残差曲线的叠加,过程如图3所示;LightGBM算法对GBDT算法进行优化,利用直方图索引和Leaf-wise生长策略[21]提高计算精确度,节约计算资源。

图3 GBDT拟合过程Fig.3 GBDT fitting process
2.1 改进LightGBM算法
在应用于电机故障在线监测过程中,传统LightGBM算法的局限性有三点。第一,将故障样本误分类为正常样本相比于将正常样本误分类为故障样本,分类精确度相同但后果严重得多,应避免。同理,对故障种类的误分类的后果要比故障严重程度误分类的后果更严重;第二,由于各种标签下的样本不能做到完全相同,样本对总体样本的估计有偏;第三,电机故障特征量较多(达20维),而相应的样本量却较少(信号处理过程复杂且相关开源数据集缺乏),因此模型容易过拟合。
针对上述问题,创新点如下:
1)针对问题一,除了定义总体准确率Acc,还定义了召回率Rec,分别如下:
(7)
其中:TP表示正确分类的故障样本数量;TN表示正确分类的正常样本数量;FN表示错误分类的故障样本数量;FP表示错误分类的正常样本数量。
2)针对问题二、三,对损失函数进行改进,引入L2正则项减少过拟合;再对故障分类赋予更高的权重,即赋予更高的类别权重;然后,为了做到总体样本的无偏估计,对正常非故障样本赋予更高的样本权重。改进方法如下:
第k棵树的损失函数为
(8)
其中:Fk-1(xi;Ak-1)表示由前k-1棵树组成的模型在参数为Ak-1的条件下对输入xi的预测值,L(yi,Fk-1(xi;Ak-1))表示损失函数。

(9)
其中:α>1且为常数,yi=0即标签号为0的样本,即正常样本赋予的权重为1,yi≠0为故障样本,赋予权重值较大。
改进后的LightGBM算法综合考虑准确率和召回率,保证电机在线监测时,正常样本的误分类为零,使误分类代价最小化;同时,可以通过不断采集新数据训练模型,使模型表现不断完善。
2.2 模型训练
首先对数据集{X′}其对应标签集{Y}按照80%、20%的比例划分为训练集和测试集。
首先根据经验对分类器设定一组超参数,调用sklearn库中的GridSearchCV模块遍历搜索,得到最优超参数如表2。
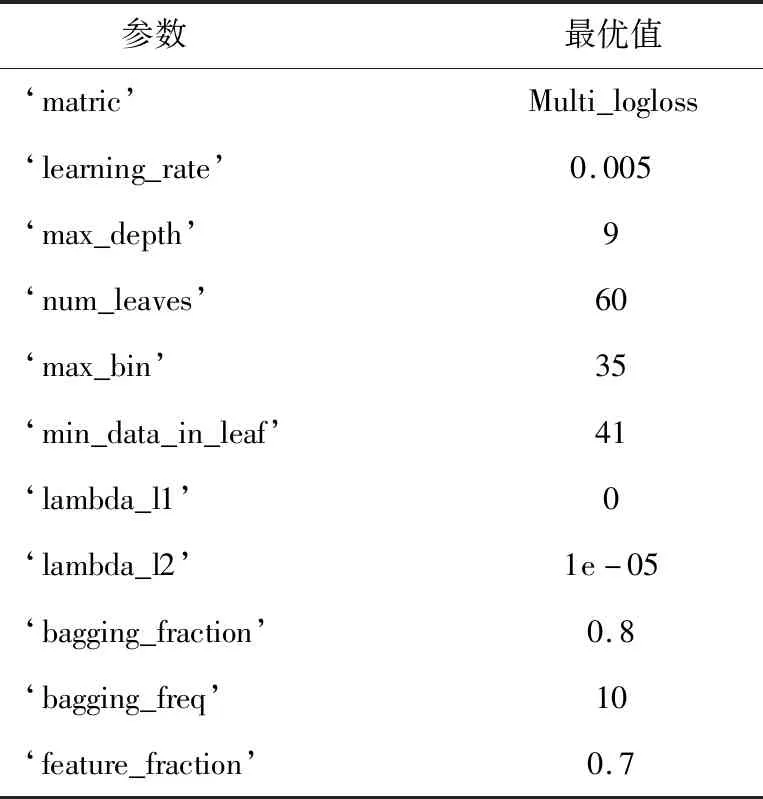
表2 超参数调节Table 2 Adjustment of hyperparameters
然后利用训练集数据训练LightGBM分类器,测试集数据对模型分类效果进行验证,并调整分类器参数,以达到最优意义下的各项参数。
3 异步电动机故障诊断方法
故障诊断方法包含3个主要流程:
1)实验数据获取与数据集生成。
进行系统、大量的实验,测取定子三相电流瞬时信号isA、isB、isC,定子三相电压瞬时信号usA、usB、usC,获得81006组样本数据;然后针对每一组数据所测得的定子三相电流、电压瞬时信号应用快速傅里叶变换提取20个故障特征量,将样本故障特征量与故障标签进行整理形成81006×20的二维输入数据集{X}和81006×1的标签{Y}。
2)故障特征量降维与重构。

3)分类器训练与保存。
将重构数据集按80%、20%划分训练集和测试集,训练集引入轻型梯度提升机分类器进行训练,利用测试集进行验证和微调,确定最优参数;最后利用pyinstaller库对模型进行封装保存。
智慧交通是随着现代计算机技术和网络技术的不断发展而产生和建立的,使用了多种具有创新性的技术,智慧交通可以使物联网技术在交通行业中得到大范围的运用。智慧交通系统在进行建立和发展的过程中,需要有高新技术的支持,未来的发展方向也比较偏向于智能化交通系统的建立,并且在此基础上与先进的计算机和网络技术结合,从而更好地解决在交通系统中出现的各种现实问题。
4 实验与结果分析
实验对象是Y100L2-4型笼型异步电动机,额定电压380 V,额定功率3 kW,额定频率50 Hz,星形连接。对实验电机分别采集满载、半载和空载情况下各种故障工况的定子电压电流信号转化为标幺值(图4,横坐标为采样点,纵坐标为电压电流标幺值),采样频率为10 600 Hz。工程实际中,电机三相参数不可能完全对称(图4),使用实验数据进行训练可以保证获得对工程数据的泛化能力。

图4 采样电流(左)、电压(右)Fig.4 Sampling current(left)and voltage(right)
由于高维空间无法实现图像可视化,先将输出层降至3个神经元,以用于对比各种自编码器的效果以及选择最合适维度特征。自编码器降维并进行分类的效果如图5。从中明显看出,将原始特征压缩至3维后,通过观察样本的分布情况,可以对标签为3、4、5、6的样本进行人工区分,但其他样本的划分需要借助分类器实现;若将原始特征压缩至二维,分类结果如图6。除标签为5、6的样本,其他样本已无法完成分类。

图5 重构三维张量图Fig.5 Reconstructed 3-dimensions figure

图6 重构二维张量图Fig.6 Reconstructed 2-dimensions figure
对栈式编码器的损失进行对比发现:当维度低于8维时,损失函数值急剧增大,因此,选择重构数据维度为8维。
对模型是否添加稀疏项的对比如图7,可以看出稀疏自编码器损失更小且更不容易发生过拟合。经过前期工作表明λ值等于10e-6时效果较好。

图7 SAE(左)和AE(右)梯度下降曲线Fig.7 Gradient descent of SAE(left)and AE(right)
表3为特征权重占比排名,权重由分类器依据特征对分类结果影响程度自动计算得出。编码后数据集分类精确度如表4,可以看出,应用栈式自编码器自动提取特征后训练精确度有所提升;应用的降噪自编码器降噪比为5%,经过结果分析,由于试验条件下负载变化较小,降噪比对精确度影响较小。但无论哪种负载下,权重排名前三的特征始终是编码后的3号、1号和0号特征,可见自编码器在数据降维方面效果显著。

表3 LightGBM特征权重Table 3 Features weight of LightGBM

表4 编码后的LightGBM精确度Table 4 Encoded data accuracy of LightGBM
图8以负序阻抗、A相电流幅值为例分析故障特征权重情况(灰度从10%到70%依次对应故障标签)。可以看出,负序阻抗对故障标签的分类大体较明显,权重较大;A相电流幅值仅可判别故障与正常样本,无法区分故障类型,权重较低。但由于负序阻抗特征拟合边界不明显,易出现误判,因此本文综合20维特征进行故障判别提高精确度。

图8 特征权重分析Fig.8 Feature weight analysis

图9 测试集混淆矩阵Fig.9 Confusion matrix of test data
最后针对实验数据集,本文使用几种主流分类器进行结果对比,各种分类器的分类精确度和每100次循环训练时间如表5。

表5 训练精确度和时间对比Table 5 Training accuracy and time comparison
可见,LightGBM不仅在训练集上可以达到100%的精确度,而且测试集精确度也是以上几种方法中最高的(高达99.83%)。同时计算所需的时间资源消耗也是最少的,综合性能最优秀,是电机故障在线监测的理想模型。
5 结 论
本文提出了一种基于SAE与改进LightGBM相结合的机器学习模型用于笼型异步电动机定子绕组匝间短路和转子断条故障的联合诊断,主要结论如下:
1)该方法可以对定子匝间短路故障和转子断条故障进行同时、联合诊断,提高了故障诊断效率。结果表明,本文在故障种类和严重程度7分类(正常、定子绕组匝间短路故障轻微、定子绕组匝间短路故障中等、定子绕组匝间短路故障严重、转子断条故障轻微、转子断条故障中等、转子断条故障严重)数据集上训练的平均精确度高达99.83%。
2)该方法仅采集定子电压、电流信号且只需进行FFT即可实现训练和诊断,符合工程实时性要求。
3)改进了传统自编码器和LightGBM算法,不仅将召回率提高到100%、降低误分类代价,同时可以有效降低过拟合,且能优化由于样本不平衡带来的有偏估计偏差。
