永磁同步电机三矢量优化预测磁链控制
2021-08-28葛兴来胡晓孙伟鑫李松涛
葛兴来,胡晓,孙伟鑫,李松涛
(西南交通大学 磁浮技术与磁浮列车教育部重点实验室,成都 611756)
0 引 言
模型预测控制(model predictive control,MPC)因其易于合并多变量约束条件和出色的控制性能等特点在学术界和工业界均受到了广泛关注[1],目前已被广泛应用于功率变换器[2]、风能转换系统[3-4]和电机[5-12]等领域。
通常MPC可分为有限控制集模型预测(finite-control-set MPC,FCS-MPC)和连续控制集模型预测(continuous-control-set MPC,CCS-MPC)。CCS-MPC可选择满足逆变器输出矢量合成范围内的所有可能开关动作,并通过SVPWM调制器合成输出,因此存在着单个控制周期内计算量沉重的问题,难以在实际工况中实现。FCS-MPC在一个控制周期内遍历所有基础电压矢量,选择使价值函数值最小的一组作为最佳电压矢量输出。整个系统无需调制器,且其可能的开关动作(切换状态)是有限的,因而实现更为简单[13]。同时,MPC又可根据单个控制周期内参与控制的电压矢量个数的不同分为单矢量MPC、双矢量MPC和三矢量MPC。单矢量MPC中,逆变器只能输出幅值和方向固定的8个基础电压矢量,因此其控制变量的输出脉动较大,稳态性能较差。为了解决以上缺陷,一般可通过扩大电压矢量选择范围进行改进。双矢量MPC中在一个控制周期内可输出两个有效电压矢量或一个有效电压矢量和一个零矢量的组合,文献[14]和文献[15]分别就以上两种组合方式提出了不同的双矢量MPC控制策略,但因第二个有效矢量的选择范围有限,在输出脉动上虽较单矢量MPC有所改善,但改善程度有限。文献[16]提出了一种广义双矢量策略,相较于文献[14]和文献[15]中所提方法,改善了系统的性能,但计算量繁杂。三矢量MPC中,通常采用两个有效电压矢量和一个零矢量的组合,达到输出电压幅值与相位均可调的目的,且整个系统开关频率固定,稳态性能良好。文献[17]通过查表法获得系统下一控制周期输出的电压序列,但其无法保证所选序列为全局最优,文献[18]将相邻电压矢量和零矢量进行分组,但其输出电压矢量覆盖范围有限。文献[19]和文献[20]提出了基于预测电流和转矩控制的三矢量MPC,提高了系统的稳态性能,但在对电压矢量进行选择时均未解决每个控制周期计算量较大这一缺陷。
在电机控制领域,根据价值函数中控制变量的不同,用于永磁同步电机(permanent magnet synchronous motor,PMSM)的MPC可分为模型预测电流控制(model predictive current control,MPCC),模型预测转矩控制(model predictive torque control,MPTC)和模型预测磁链控制(model predictive flux-linkage control,MPFC)。MPCC主要针对dq轴电流变化,以使dq轴电流误差最小的电压矢量作为其最佳电压矢量输出,尽管其在实际应用时易于实现,但在状态切换时转矩脉动较大。MPTC将电机的转矩和磁链误差视为控制变量,还可以通过控制多个目标来降低开关频率[21]。与MPCC相比,MPTC在状态切换时控制变量过冲较小,但由于磁链和转矩的量纲不同,往往需要在价值函数中加入权重系数。权重系数的选取主要取决于经验方法,但由于指导权重系数的设计与调整的方法很少,增加了MPTC的复杂性。文献[22]在矩阵变换器的预测控制中引入模糊逻辑来实时调整权重系数,文献[23]在转矩和磁链方面分别采用两个价值函数来避免权重系数的存在,但该方法增加系统的计算量。对于MPFC,价值函数仅将磁链作为控制变量,这意味着不再需要权重系数,同时还可实现与MPTC相当的控制性能。文献[24]和文献[25]提出了针对不同电机的预测磁链控制方法,但只完成了将磁链作为控制变量进行基础预测控制。虽然MPFC存在诸如繁重的计算量、磁链值无法保持恒定等问题,但仍然是未来电机控制的发展趋势。
基于上述分析,本文提出了一种基于矢量快速选择的永磁同步电机三矢量预测磁链控制。第一节首先给出永磁电机的模型,并介绍传统的模型预测控制方法。在此基础上,第二节首先对矢量扇区进行重新划分。在该步骤中,根据磁链无差拍预测控制原理计算下一周期预施加的参考电压矢量,从而将价值函数中对磁链误差的跟踪转化为对电压误差的跟踪,减少每个控制周期的预测次数。随后详细介绍了三矢量优化预测磁链控制,其中,推导磁链与基础电压矢量的关系,根据新划分的矢量扇区对第一个最佳电压矢量进行快速选择,并将其作用结果与无差拍原理计算所得的磁链参考值进行比较,两者的差值作为第二个最佳电压矢量选择的标准。两个有效矢量和一个零矢量的作用时间根据无差拍控制原理计算得出。第三节利用仿真和实验测试对所研究的模型预测控制方法进行验证,并与传统预测磁链控制进行对比。最后,在第四节中对全文进行总结,得出结论。
1 传统预测磁链控制
1.1 PMSM数学模型
以表贴式永磁同步电机为例,其在同步旋转坐标系下的电流状态方程和磁链方程为:
pis=Ais+Bus-C;
(1)
ψs=B-1is+D。
(2)
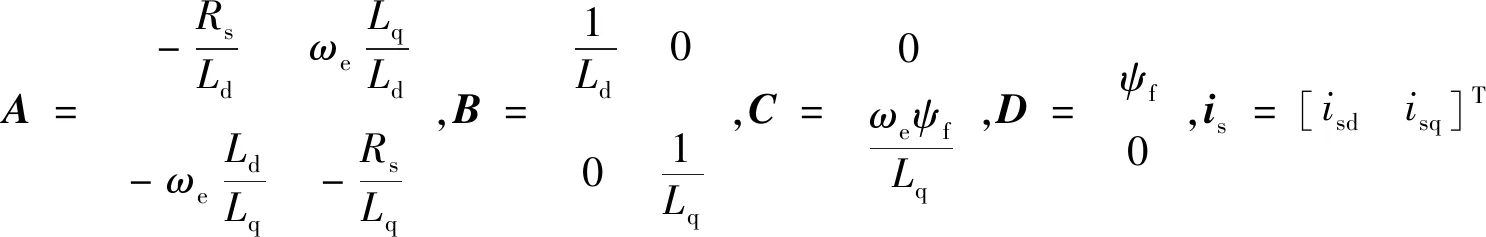
对于PMSM来说,通常永磁磁链值已知,则磁链参考值和转矩参考值满足以下方程[24]:
(3)
式中:np为电机极对数;|ψs_ref|为定子磁链参考值;θsf为定子磁链参考值与永磁磁链之间的夹角,即电机理想负载角。当控制定子直轴电流isd=0时,定子磁链参考值与理想负载角可表达如下:
(4)
(5)
定子磁链参考矢量角度为
∠ψs_ref=∠ψf+θsf。
(6)
结合式(4)~式(6),定子磁链参考矢量可表达为
ψs_ref=|ψs_ref|ej∠ψs_ref。
(7)
1.2 PMSM预测磁链控制
定子磁链与定子电流之间满足关系式:
(8)
对式(8)采用一阶欧拉离散化,可得下一时刻磁链预测表达式:
(9)
定子磁链参考值在d、q轴上的分量为:
(10)
PMSM的传统预测磁链控制以磁链作为控制变量,逆变器的8个基础电压矢量代入式(9)后可得到对应的8组磁链预测值,依次代入价值函数中并输出使价值函数最小的磁链预测值所对应的基础电压矢量,其控制框图如图1所示。磁链预测控制价值函数为
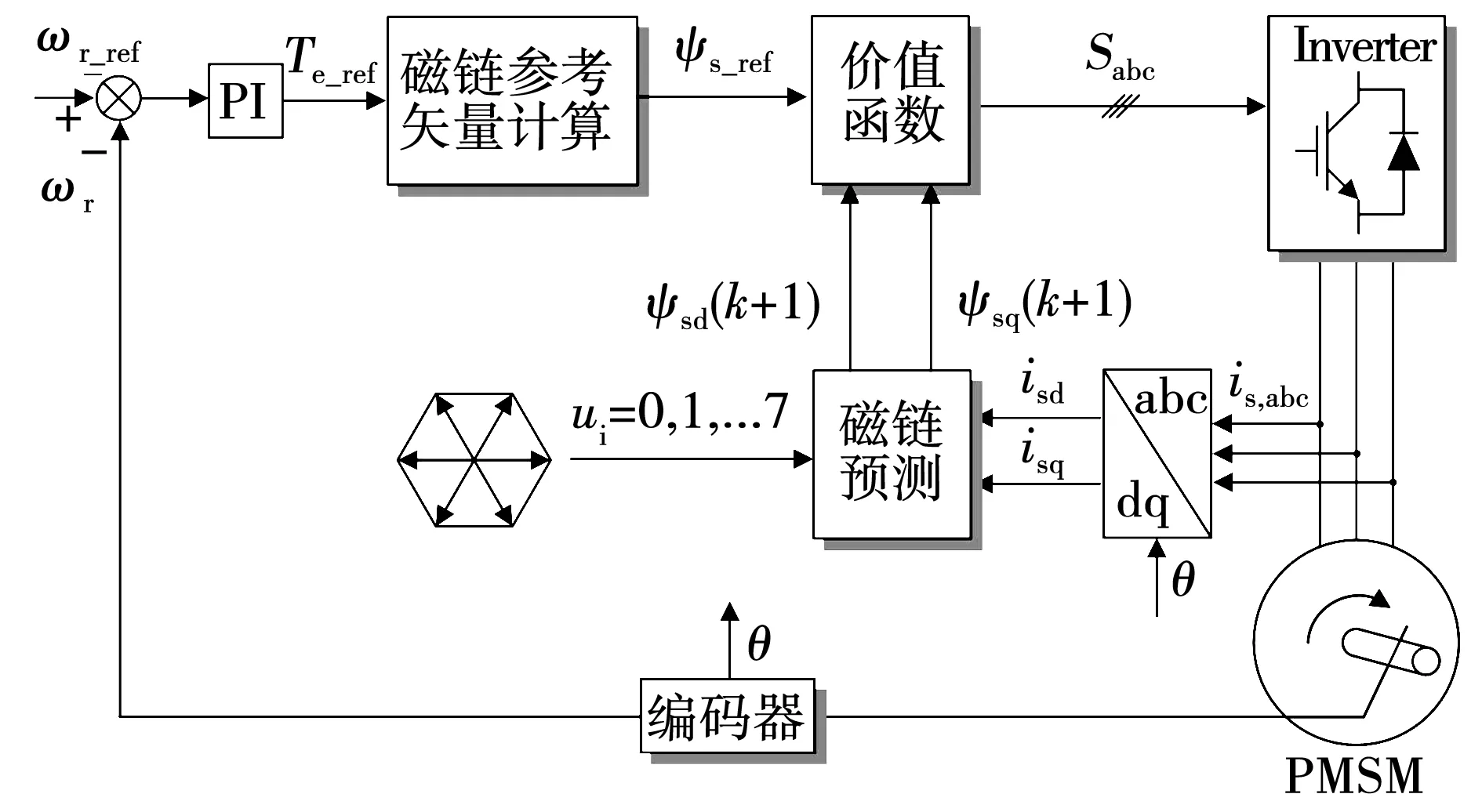
图1 传统预测磁链控制框图Fig.1 Block diagram of the conventional model predictive flux-linkage control
g=|ψsd_ref-ψsd(k+1)|+|ψsq_ref-ψsq(k+1)|。
(11)
2 三矢量优化预测磁链控制
2.1 优化矢量扇区划分
传统预测磁链控制在单个控制周期内需遍历所有基础电压矢量,即需预测8次并对价值函数进行8次对应计算,经比较后再输出最佳电压矢量,其计算量较大,在实际应用时性能往往受到一定限制。将矢量扇区进行重新划分,根据磁链无差拍预测控制原理计算下一周期预施加的参考电压矢量,从而将价值函数中对磁链误差的跟踪转化为对电压误差的跟踪,根据相位判断参考电压矢量所在扇区后与相邻基础电压矢量进行比较,该种方法无需遍历所有基础电压矢量,可显著减少系统计算量。
对于PMSM,其定子磁链与定子电压之间满足关系式:
(12)
对式(12)采用一阶欧拉离散化后可得:
(13)
其中Ts为采样周期。
根据无差拍控制原理,令下一时刻的磁链达到参考值,即
(14)
可得理想电压矢量为:
(15)
将理想电压矢量在同步旋转坐标系上的分量转化为在两相静止坐标系上的分量,可得理想电压矢量相位为
(16)
对矢量扇区进行如表1所示的重新划分,根据理想电压矢量相位判断其所在扇区,可确定待选有效电压矢量。
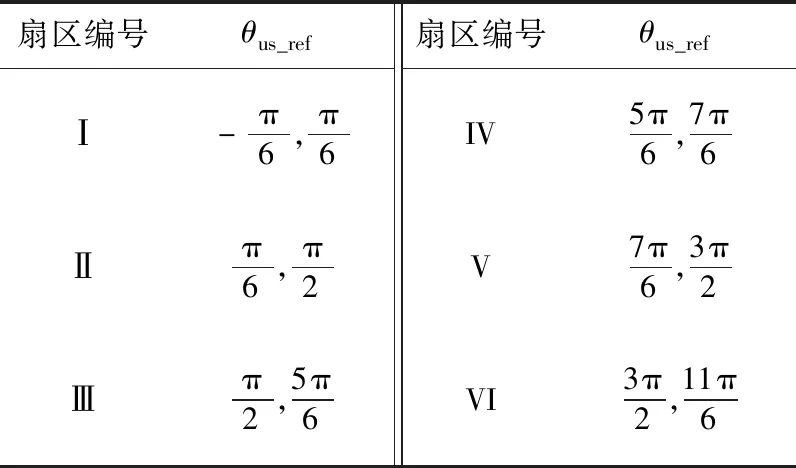
表1 新矢量扇区划分Table 1 New vector division
将价值函数改写成如下形式:
g=|us_ref-ui|。
(17)
将待选有效电压矢量与零矢量分别代入式(17)中进行计算,通过比较理想电压矢量与所在扇区的有效电压矢量和零矢量间的电压误差大小,即可判断出下一时刻预施加的最佳电压矢量。矢量扇区重新划分后的控制框图如图2所示。

图2 基于新矢量扇区划分的预测磁链控制框图Fig.2 Block diagram of the MPFC based on new vector division
2.2 有效电压矢量选择
为了解决传统预测磁链控制由于输出电压矢量的幅值、相位固定所造成的在转矩脉动大、电流谐波较多等方面的局限性,在矢量扇区重新划分和价值函数跟踪电压误差的基础上提出三矢量优化预测磁链控制,即在每个控制周期内输出两个有效电压矢量和一个零矢量的组合,达到输出电压矢量在幅值和相位上均可控制的目的。三矢量优化预测磁链控制框图如图3所示。

图3 三矢量优化预测磁链控制Fig.3 Block diagram of the improved three-vector MPFC
首先根据优化预测磁链控制确定第一个最佳电压矢量uo1,计算该电压矢量与理想电压矢量间的误差矢量Δu,然后求解误差矢量Δu在两相静止坐标系上的分量,判断其所在扇区,直接选择第二个最佳电压矢量uo2,其矢量选择如表1所示。
2.3 作用时间计算
令ud_o1、uq_o1、ud_o2、uq_o2、ud0、uq0分别为第一个最佳电压矢量uo1、第二个最佳电压矢量uo2和零矢量在d、q坐标轴上的分量;Sd_o1、Sq_o1、Sd_o2、Sq_o2、Sd0、Sq0分别为第一个最佳电压矢量uo1、第二个最佳电压矢量uo2和零矢量作用时定子磁链所对应的变化率,其计算公式如下:
(18)
(19)
(20)
采用磁链无差拍原则计算各矢量作用时间,即下一时刻磁链值与磁链参考值相等,则满足:
(21)
其中:t1、t2、t0分别为3个矢量作用时间,且t0=Ts-t1-t2。
联立式(18)~式(21)可求解得出:
(22)
其中:X1=ud_o2uq_o1-uq_o2ud_o1;
X2=ψsq_ref-ψsq(k)-Sq0Ts;
X3=ψsd_ref-ψsd(k)-Sq0Ts。
对于计算所得的矢量作用时间t1、t2、t0,若其中有小于零的计算结果,则舍去相应作用矢量,由剩余两个矢量作用整个控制周期。若t1+t2>Ts,则按下式重新分配矢量作用时间:
(23)
3 仿真与实验分析
3.1 仿真分析
为了验证三矢量优化预测磁链算法的可行性,首先基于MATLAB/Simulink搭建了系统仿真模块,系统控制频率设置为20 kHz。其中,永磁同步电机的参数如表2所示。
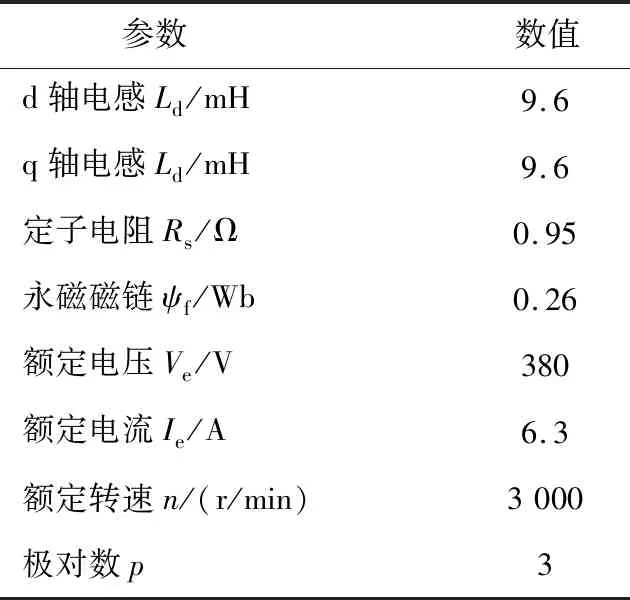
表2 永磁同步电机参数Table 2 Parameters of the PMSM
仿真中,电机首先空载起动,由零转速升至额定转速3 000 r/min。稳定运行后在1s时突加负载10 N·m,随后在2s时将负载由10 N·m减载至5 N·m运行。测试结果如图4和图5所示,从上至下依次是定子三相电流波形、转速波形和转矩波形。

图4 传统预测磁链控制仿真结果Fig.4 Simulation results of the conventional MPFC method
通过图4与图5对比,三矢量优化预测磁链控制和优化磁链预测达到转速给定值的时间分别为0.155 s和0.156 s,二者控制响应速度相当,但前者电流脉动和转矩脉动明显更小。为了进一步对比两种控制方法的控制性能,图6和图7给出了两种控制方法在额定转速及额定负载下的谐波分析。由图6和图7对比可以看出,三矢量优化预测磁链控制的电流谐波含量明显小于优化预测磁链控制,其稳态性能更佳。
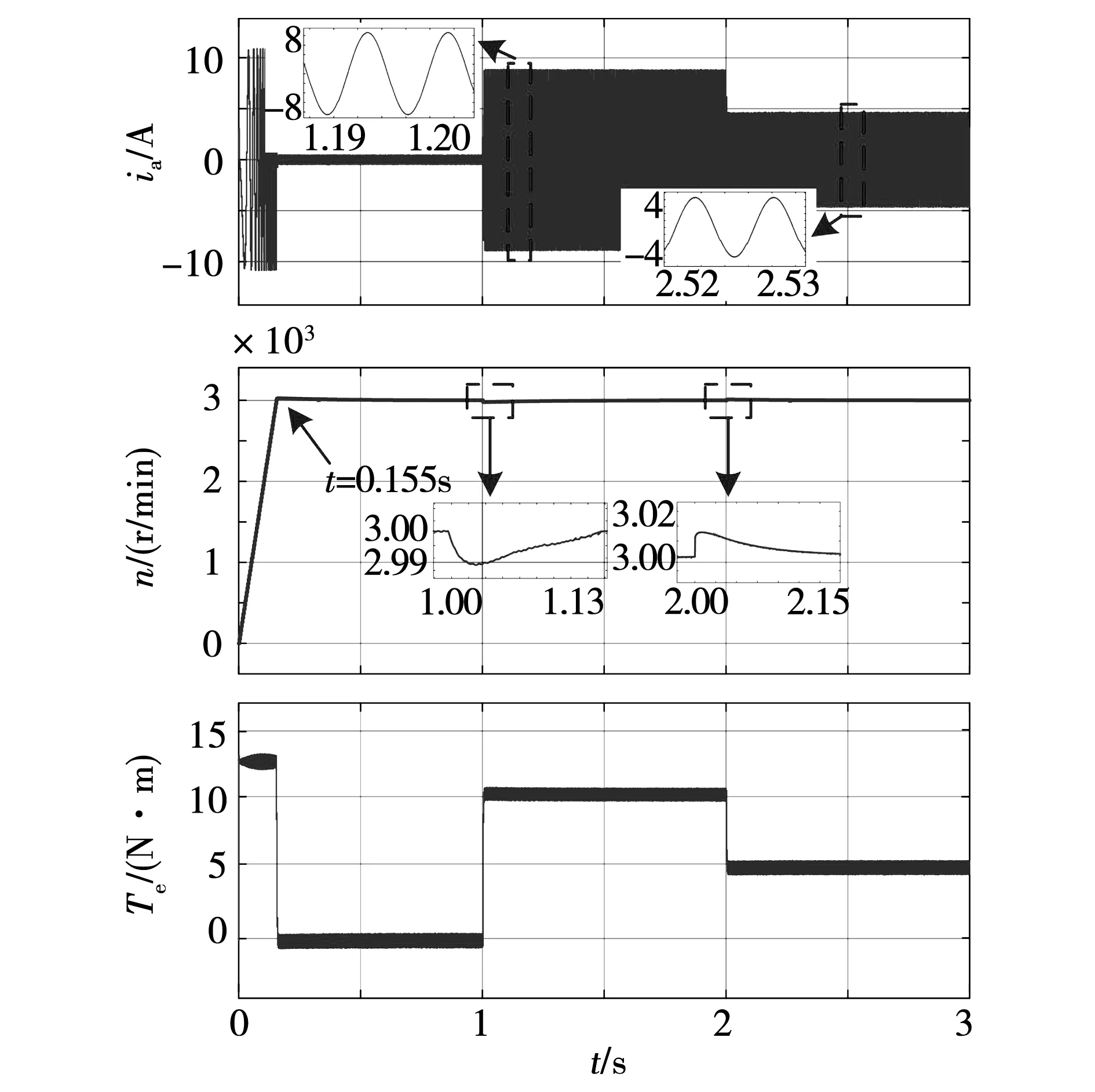
图5 三矢量优化预测磁链控制仿真结果Fig.5 Simulation results of the improved three-vector MPFC
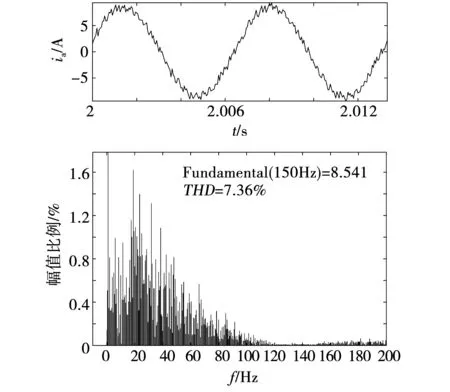
图6 传统预测磁链控制定子电流谐波分析Fig.6 FFT analysis of stator current based on the conventional MPFC
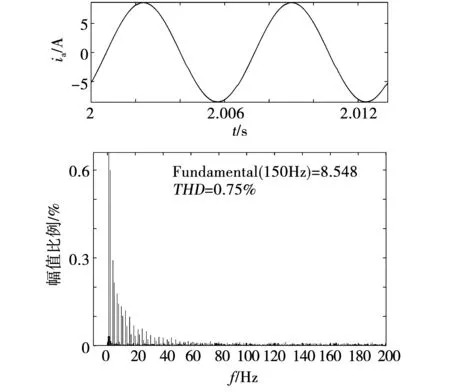
图7 三矢量优化预测磁链控制定子电流谐波分析Fig.7 FFT analysis of stator current based on the improved three-vector MPFC
3.2 实验分析
利用基于RT-LAB实时仿真器和数字信号处理器TMS320F28335的硬件在环测试平台,如图8所示,进一步验证所提出的三矢量优化预测磁链控制算法。其中,被控对象基于MATLAB/Simulink建模,通过TCP/IP下载到实时仿真机中模拟真实被控逆变器-电机系统。永磁同步电机的参数如表2所示。
1)稳态性能。
为了对比优化预测磁链控制与三矢量优化预测磁链控制算法的稳态性能,电机在额定转速3 000 r/min和额定负载10 N·m下运行,其实验波形如图9和图10所示,通过从示波器中截取数据分别对电流和转矩脉动进行计算,两种控制方法下的稳态性能对比如表3所示。
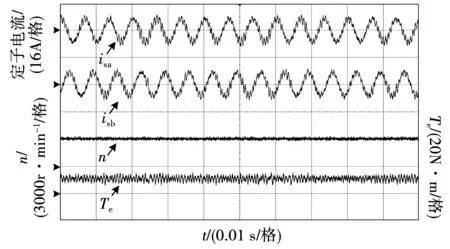
图9 传统预测磁链控制稳态运行实验结果Fig.9 Experimental results of the conventional MPFC under steady-state operation
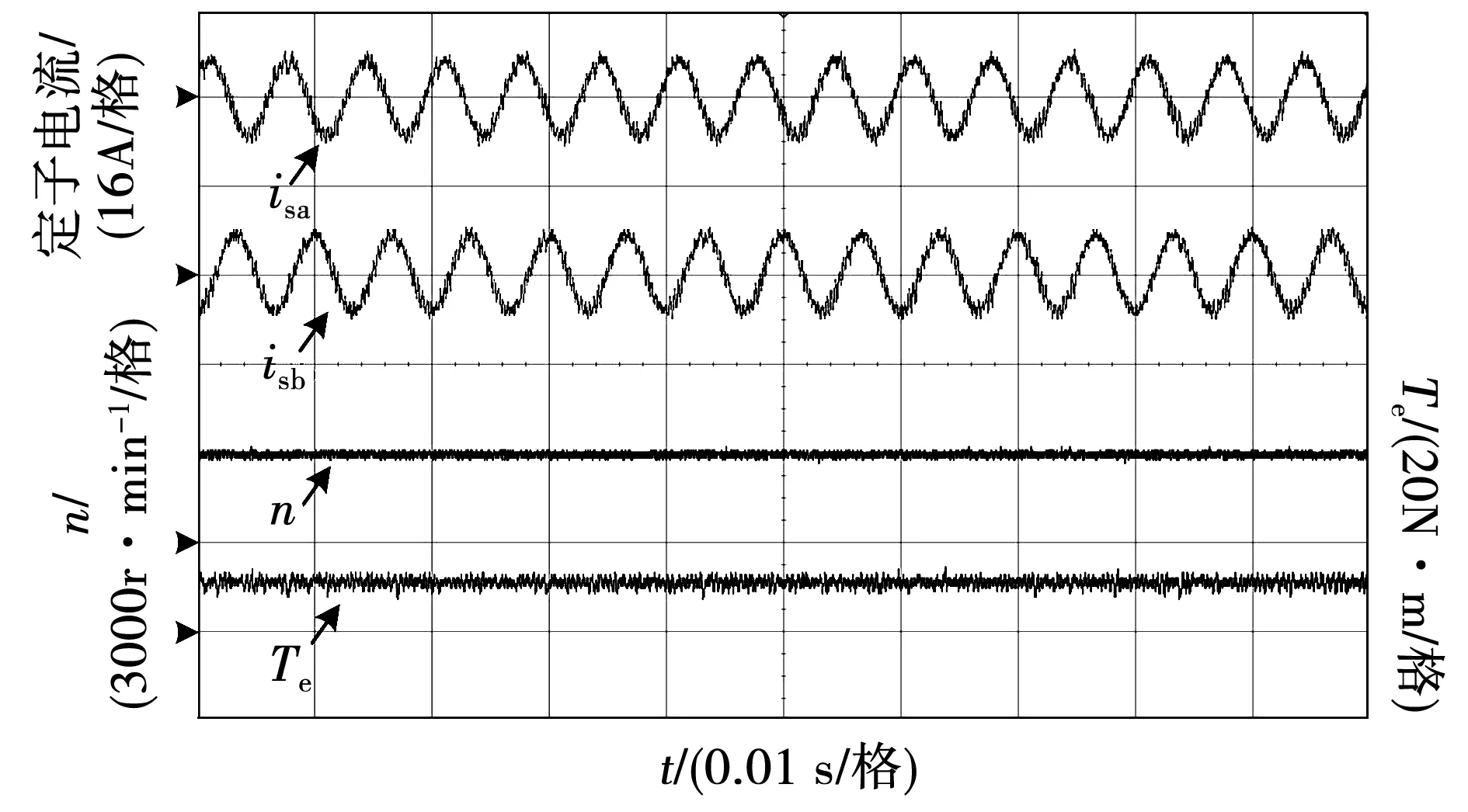
图10 三矢量优化预测磁链控制稳态运行实验结果Fig.10 Experimental results of the improved three-vector MPFC under steady-state operation

表3 三矢量优化预测磁链控制与传统预测磁链控制稳态性能对比Table 3 Steady-state performance comparison between the improved three-vector MPFC and the conventional MPFC
由实验结果分析可知,优化预测磁链控制虽然控制简单,但其存在电流及输出转矩脉动均较大等问题,而三矢量优化预测磁链控制在电流及输出转矩脉动均得到有效抑制,稳态性能明显提高。
2)动态性能。
为了对比优化预测磁链控制与三矢量优化预测磁链控制算法的动态响应性能,首先设置了一组电机正反转工况,永磁同步电机在空载情况下运行。实验波形如图11和图12所示。从实验波形图对比可以看出,永磁同步电机在两种控制方法下实际转速都能时刻跟踪给定转速,切换过程中转速保持平稳,且过零点处系统稳定,动态性能良好。
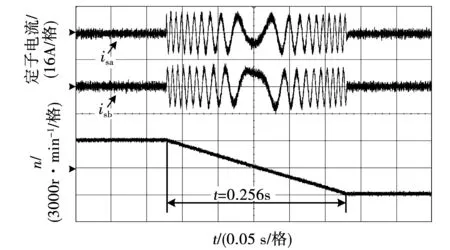
图11 传统预测磁链控制电机正反转实验结果Fig.11 Experimental results of the conventional MPFC under motor forward and reverse

图12 三矢量优化预测磁链控制电机正反转实验结果Fig.12 Experimental results of the improved three-vector MPFC under motor forward and reverse
为了进一步对比优化预测磁链控制与三矢量优化预测磁链控制算法的动态响应性能,分别设置了负载突变和转速突变两组对比实验。其中,负载突变实验中永磁同步电机以额定速度3 000 r/min运行,负载由10 N·m突然减至5 N·m。转速突变实验中永磁同步电机在额定负载下运行,转速由3 000 r/min降至1 500 r/min。实验波形如图13~图16所示。在负载突变实验中,两种控制策略均能在几乎不影响转速的情况下跟踪给定负载,但在负载切换时,三矢量优化预测磁链控制下的定子电流脉动更小,在负载切换时能平滑过渡。在转速突变实验中,三矢量优化预测磁链控制的响应时间与传统预测磁链控制的响应时间近似一致。由于三矢量优化预测磁链控制减少了计算量,因此虽然控制算法更为复杂,但在动态响应上却与传统控制方法相似,且前者在速度切换时的电流波形更为平滑,因此较优化预测磁链控制更佳。
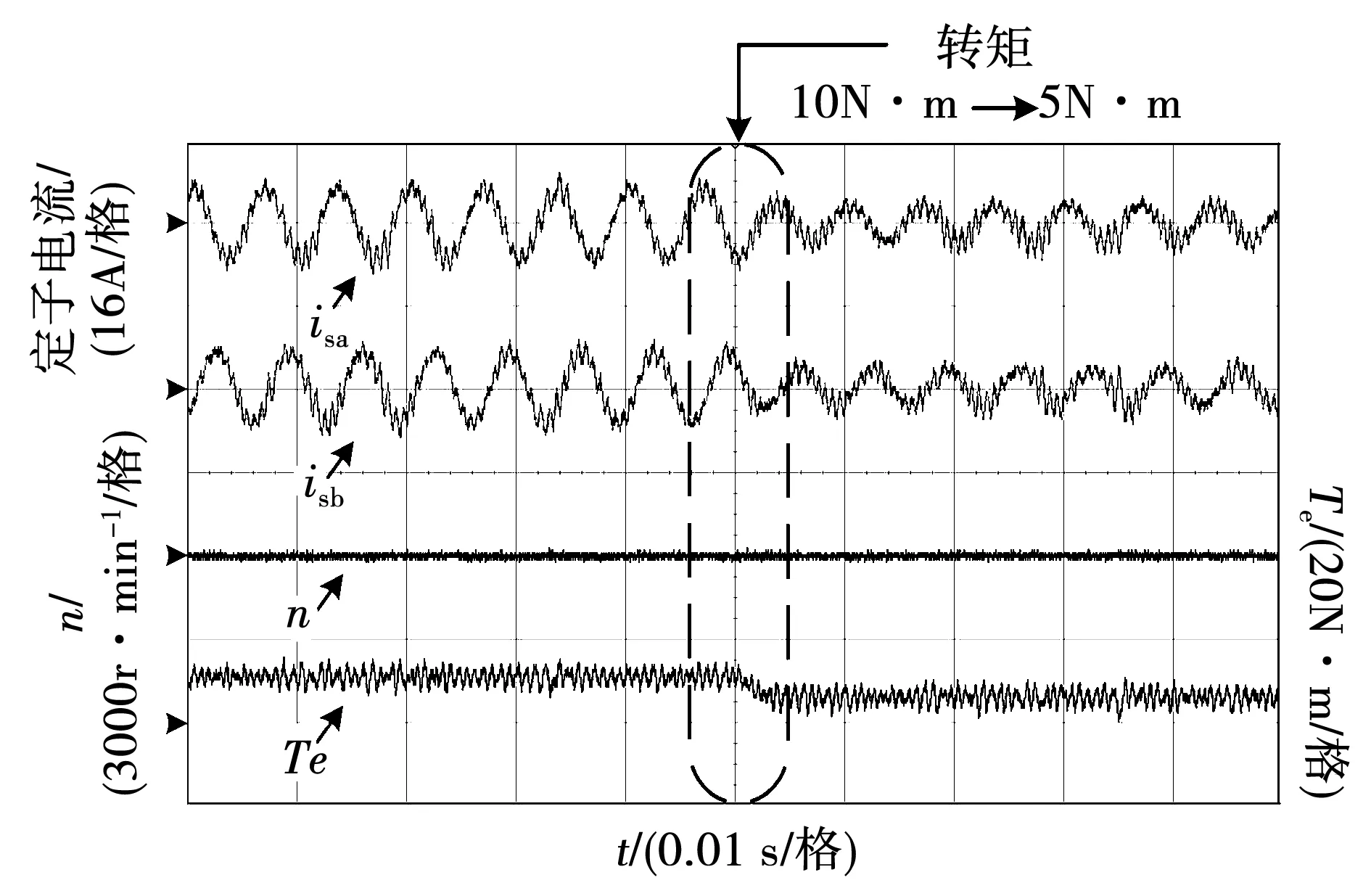
图13 传统预测磁链控制负载突变实验结果Fig.13 Experimental results of the conventional MPFC under load variations
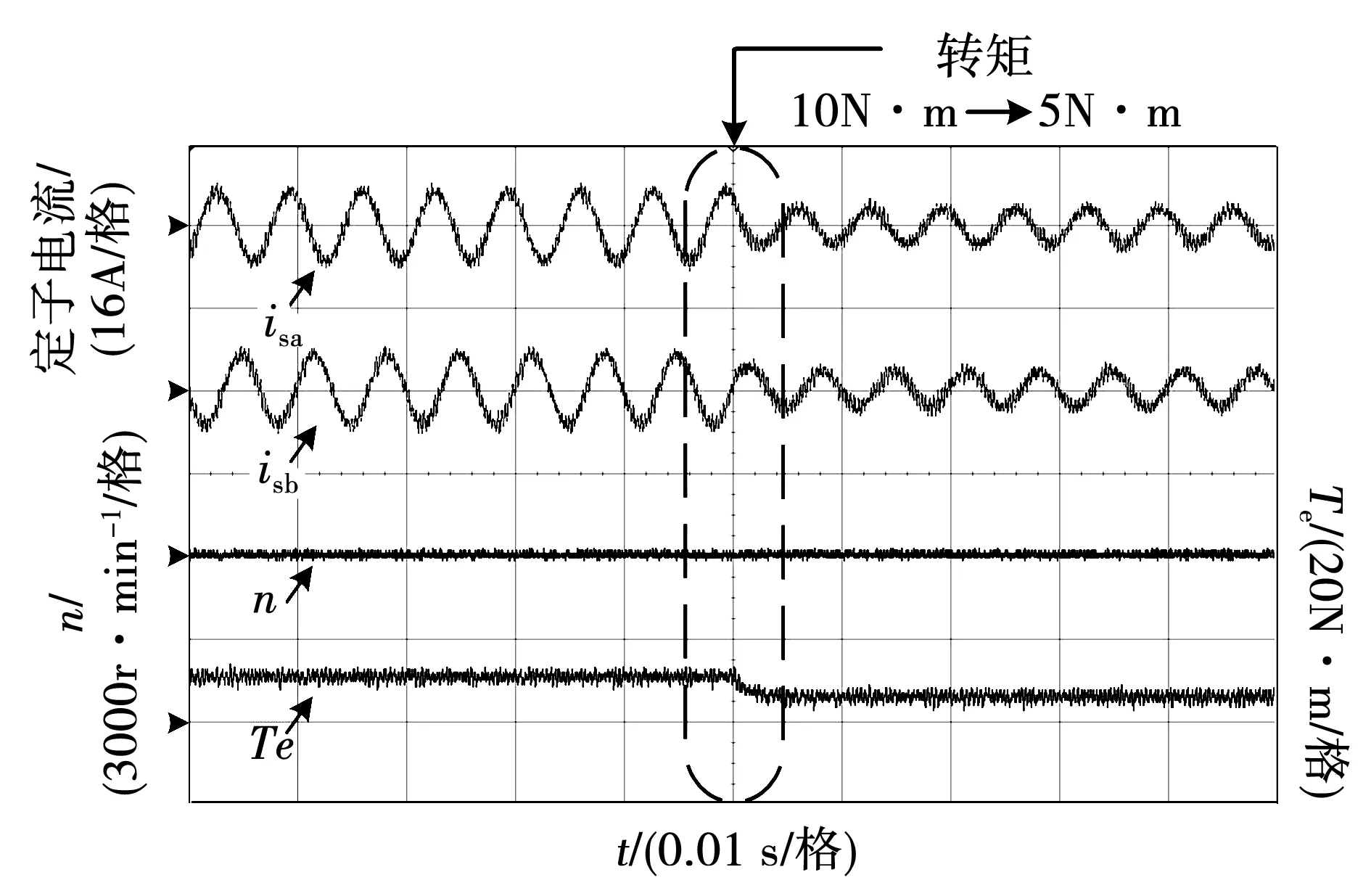
图14 三矢量优化预测磁链控制负载突变实验结果Fig.14 Experimental results of the improved three-vector MPFC under load variations
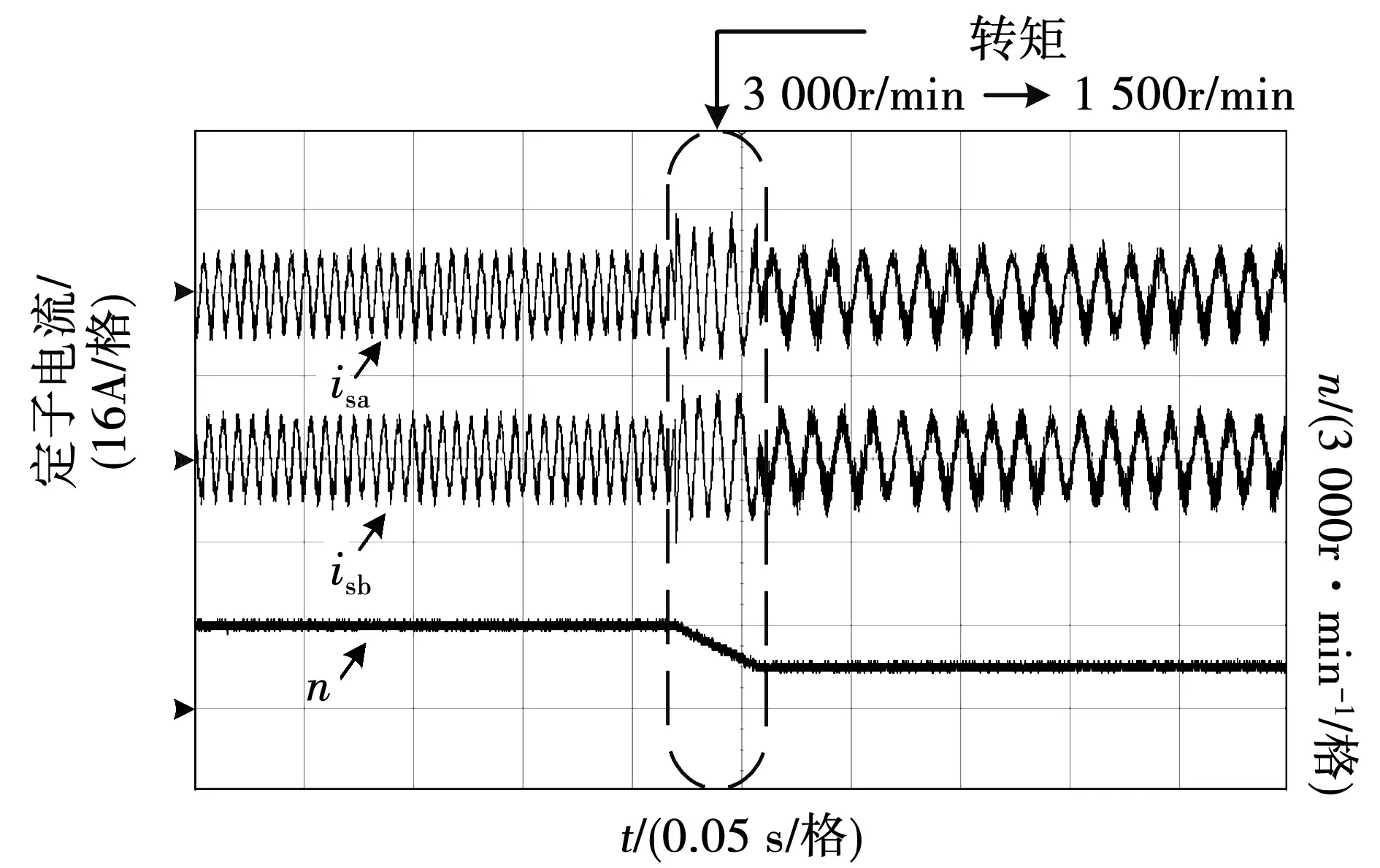
图15 传统预测磁链控制转速突变实验结果Fig.15 Experimental results of the conventional MPFC under speed command variations
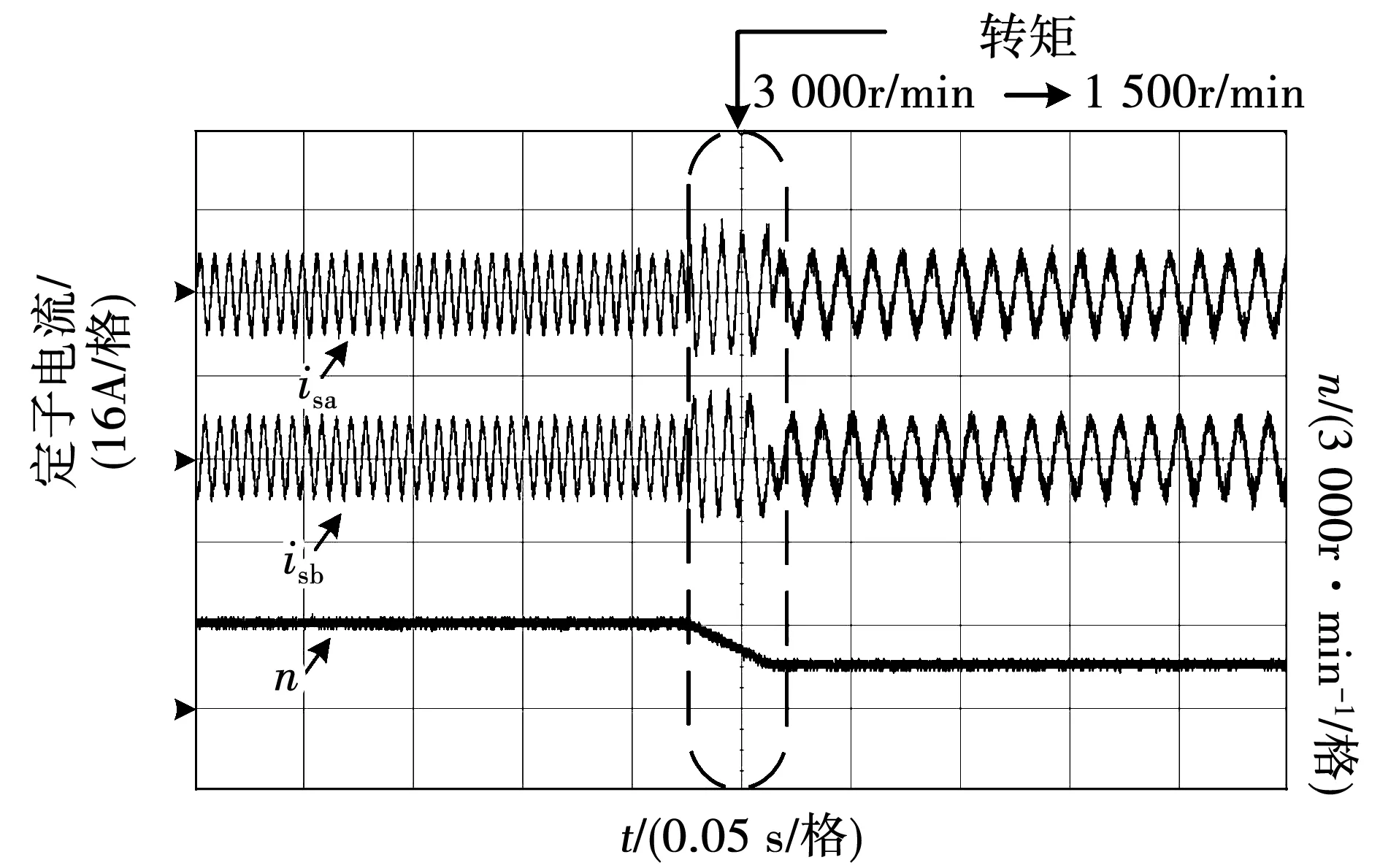
图16 三矢量优化预测磁链控制转速突变实验结果Fig.16 Experimental results of the improved three-vector MPFC under speed command variations
4 结 论
为了减少永磁同步电机传统预测磁链控制的计算量及系统输出脉动,本文研究一种三矢量优化预测磁链控制方法,在该方法中,单个控制周期内输出一个由两个基础有效电压矢量和零矢量合成的虚拟电压矢量,使系统输出电压矢量的覆盖值变大,开关频率固定。通过仿真及实验验证可得出:提出的三矢量优化预测磁链控制在电机正反转、负载突变和转速突变情况下具有和传统预测磁链控制相当的动态响应速度,可对系统给定值进行快速跟踪。与此同时,三矢量优化预测磁链控制的电流脉动及转矩脉动明显减小,其稳态性能明显优于传统预测磁链控制,能实现更好的控制效果。
