永磁同步电机无参数超局部模型预测控制
2021-08-28史涔溦解正宵陈卓易邱建琪
史涔溦,解正宵,陈卓易,邱建琪
(1.浙江大学 电气工程学院,杭州 310027;2.浙大宁波理工学院 信息科学与工程学院,浙江 宁波 315100)
0 引 言
永磁同步电机(permanent magnet synchronous machine,PMSM)具有高功率密度、高效率和宽调速范围的优点,在许多生产生活领域中都得到了广泛的应用[1]。为了进一步满足经济社会发展对永磁同步电机调速性能的需求,研究人员提出了许多高性能控制策略,如预测控制,滑模控制和神经网络控制等[2]。有限集模型预测控制(finite set model predictive control,FCS-MPC)的核心思想是对系统未来的状态量进行估计,在每个控制周期内,FCS-MPC控制器都要对控制目标的完成一次状态预测计算,在有限的控制集内选出使代价函数最优的控制策略[3]。
PMSM的电磁转矩是由定子电流产生的磁场与转子磁场相互作用产生的,FCS-MPC如果使用定子d-q轴电流作为预测和控制的对象,则被称为模型预测电流控制(model predictive current control,MPCC)。MPCC方法通常使用电流预测值和电流参考值之间偏差来设计代价函数,电流的参考值由转速外环的PI控制器给出。在一些研究中,研究人员为了获得更快的响应速度舍弃了转速环和电流环的级联结构,将电机的转速和转矩也引入预测模型中,这种方法一般被称为模型预测转矩控制或者模型预测转速控制[4-7]。
MPCC方法的预测精确度十分依赖于模型的准确程度,然而在实际应用中,铁磁材料的饱和效应和交叉耦合[8]、逆变器的扰动电压[9],温升对电阻和磁链的影响[10]等未建模因素都会影响模型的预测精确度,并且在电机参数无法提前预知的情况下,参数失配也会导致控制性能下降。为了提高MPCC方法的鲁棒性,研究人员提出许多自适应的参数辨识方法,这些方法一般对PMSM的电感Ld、Lq,定子电阻Rs,转子永磁体磁链ψf中的一个或者多个进行在线观测。然而在电机稳态运行时,观测器由于欠秩问题无法准确识别出所有的4个参数,尤其是Ld和ψf无法被独立的观测[11]。
为了克服传统MPCC方法对参数的依赖,一些研究者提出了无模型电流预测控制 (model-free predictive current control,MFPCC),有时也被称作无参数模型预测控制。在早期的MFPCC研究中,研究人员直接建立了电压矢量与和电流变化量之间的查找表(look-up table,LUT),在每次应用电压矢量后更新LUT中相应的电流变化量。在某个电压矢量长时间没有使用的情况下,这种方法存在LUT更新停滞问题,容易造成预测误差增大,并且对电流尖刺的抗干扰能力较差[12]。为了解决LUT更新停滞问题,一些研究人员通过对最近使用的3个不同电压矢量进行组合来代替其他未使用过的电压矢量,从而更新所有电流变化量,这种方法显著提高了LUT更新频率[13]。一些MFPCC方法中还研究了转子转动对电压矢量作用效果的影响,使用转子位置补偿方法来提高预测精确度[14]。这些基于LUT的MFPCC方法基本上直接使用了以往的电流数据进行预测,具有运算量小的优势,但控制性能受电流传感器精确度的影响比较大,方法的稳定性和抗干扰能力有待提升。
本文提出一种基于电机超局部模型的MFPCC方法,将每周期电流变化量中与电压相关的部分视为电流的受迫响应分量,其他所有与电机运行状态相关的部分视为电流的自然响应分量,并设计稳定程度高的观测器来估计电压对电流作用系数。在电机参数未知的情况下,控制性能优于存在参数失配的MPCC方法,并且在突增负载的情况下也有良好的动态性能。
1 有参数MPCC方法
忽略磁场交叉耦合等因素的影响时,PMSM在d-q轴旋转坐标系下的电压方程为:
(1)
式中:ud、uq分别为d、q轴电压;Rs为定子电阻;id、iq分别为d、q轴电流;ld、lq分别为d、q轴动态电感;ωe为电角速度;Ld、Lq分别为d、q轴静态电阻;ψf为转子永磁体磁链。将式中电流的微分项通过前向欧拉法转化为离散形式,得到PMSM的电流预测模型为:
(2)
式中:右上标“P”标表示预测值,Ts为预测步长。在忽略饱和效应时,可以认为动态电感等同于静态电感,式中的ld、lq一般使用Ld、Lq来代替。
FCS-MPCC的代价函数常采用电流预测值与参考值之间的空间距离来表示,一般的形式为
(3)
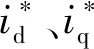
由于实际应用中微处理器的计算需要一定时间,即便在每次计算完成后立即输出控制结果,也会存在延时问题,使得被选中的电压矢量本非计算当前时刻最优的选择,造成控制性能的劣化。所以在模型预测控制的实际应用中,大多数FCS-MPCC的应用中都采用了分两步预测的延时补偿方式,预测流程如图1所示。

图1 预测延时补偿流程Fig.1 Prediction delay compensation procedure
上图中预测模型在参数准确的理想情况下,预测得到的k+1时刻的电流估计值与真实电流值相同,被选中的k+1时刻电压矢量即为最优的控制矢量,这样便消除了由计算延时带来的误差。
在实际应用中,FCS-MPCC在参数失配时存在电流控制误差问题,电流参考值与真实值不相等[15],稳态电流控制误差的计算公式为:
(4)
式中:Id、Iq为稳态时d-q轴电流的平均值;符号Δ表示控制参数减去真实参数的差值;符号^表示控制中使用的参数估计值。
2 无参数模型预测控制方法
无参数模型预测控制方法具有自适应能力强的优点,传统的MFPCC方法直接使用前几个周期的电压矢量和电流值进行电流预测,虽然具有运算量小的优势,但控制器的预测精确度和稳定性不够理想。基于PMSM的超局部电流模型提出了一种新的MFPCC方法,并针对电流的自然响应和受迫响应提出了不同的在线计算方法,在保留MFPCC方法自适应能力的同时提高了控制器的稳定型和抗干扰能力。
2.1 PMSM的超局部模型
在每个控制周期内,永磁同步电机的d-q轴电流变化量可以分解为两部分,一部分是电压作用下的受迫响应,另一部分是与电压无关的电流自然响应。如果近似认为电流的受迫响应与电压值线性相关,离散形式的一阶超局部模型可以表示为:
(5)
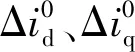
将式(4)与式(2)中传统的PMSM电流模型进行对比,可知无参数模型中的变量与传统PMSM模型参数之间的对应关系为:
(6)
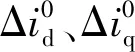
有参数的FCS-MPCC中通常使用静态电感Ld、Lq代替动态电感ld、lq,而提出的MFPCC方法中无需进行这种替换,所以消除了饱和效应带来的误差。
2.2 电流自然响应计算方法
(7)
对过去3个控制周期内的d-q轴电流变化量也使用同样的系数x1、x2、x3进行加权,电流变化量的矢量和为
(8)
将式(4)中PMSM的超局部模型代入式(7),电流矢量加权和可以表示为
(9)
由式(6)可知式(8)中电压矢量加权之和为零向量,式(8)可以重新写为
(10)
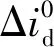
(11)
满足式(6)中线性代数方程成立的系数x1、x2、x3有无数对,在3个电压矢量均不相同的情况下,本研究中使用下式来得到满足条件系数
(12)
2.3 电压作用系数在线辨识
递推最小二乘法具有收敛速度快、观测结果稳定的优点[16]。电压作用参数α1、α2受PMSM运行状态的影响较小,但对整体的预测精确度影响很大,所以本研究中使用带有遗忘因数的递推最小二乘法来观测α1、α2,观测器的状态方程为:
(13)
式中:k1、k2是卡尔曼增益系数,e1、e2为电流变化量测量值与预测值之间的误差,它们的计算公式为:
(14)
式中:λ为遗忘因数,取值范围是(0,1),λ越趋近于0观测器收敛的越快,越趋近于1观测结果越稳定;p1、p2为相关性系数,在观测器初始化时需要被赋上合适的初始值。
3 仿真验证
为了验证方法的有效性,在Simulink中搭建PMSM控制系统的仿真模型,仿真中直流母线电压Udc为120 V。由于提出的MFPCC方法无需得知Udc的数值,为了体现自适应控制的特点,在仿真以及后续的实物实验中均令控制器默认Udc为100 V,无需与实际Udc其保持一致,所影响的仅仅是α1、α2的观测值。仿真所用电机的主要参数如表1所示。

表1 仿真中PMSM主要参数Table 1 Parameters of PMSM in simulation
仿真中设定速度参考值为360 r/min,令d轴电流参考值为0,q轴电流参考值由速度环PI控制器给出,取PI控制器参数Kp=0.003 4,Ki=0.017。电机空载启动,在6 s时突增2 N·m负载。电机在动态过程中转速以及电流的控制效果如图2所示。
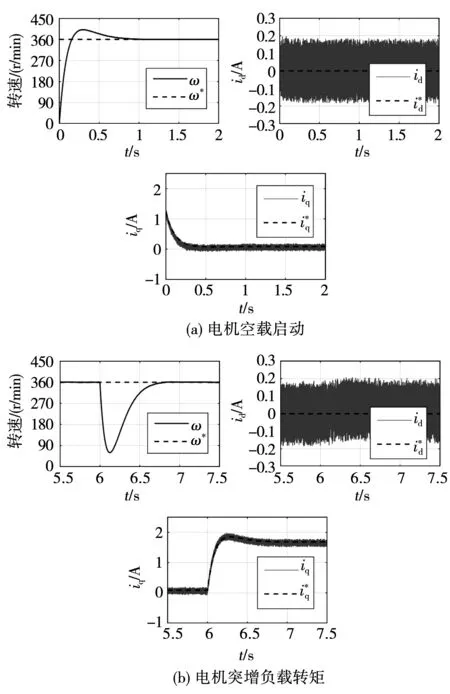
图2 PMSM动态控制效果Fig.2 Dynamic performance of PMSM
图2中PMSM在空载启动时能快速到达指定转速,在突增负载时电机也能够迅速恢复到初始转速。图中q轴电流的响应速度十分迅速,控制器表现出了良好的动态控制性能。为了更直观地体现控制器中内部参数值的变化,将整个仿真过程中的电流预测误差以及参数观测值绘制在图3中。

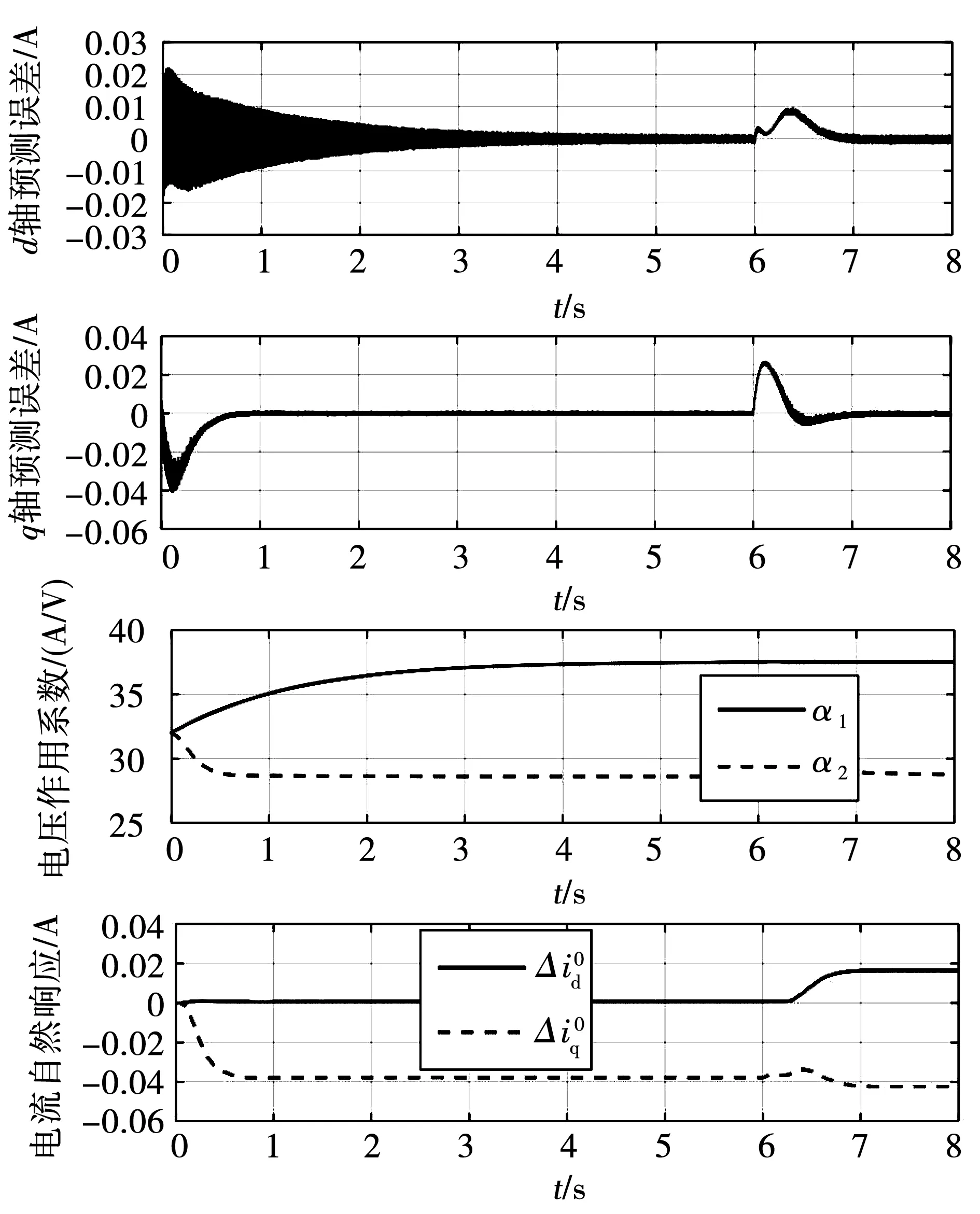
图3 观测器参数辨识效果Fig.3 Parameter identification results of observers
4 实验验证
为了进一步验证提出的MFPCC方法的控制性能,搭建了dSPACE实验平台进行实物实验,实验中的电源采用了120V直流稳压源,通过三相两电平电压源型逆变器为PMSM供电,实验中所用PMSM除转动惯量和阻尼系数外均与仿真中的参数一致。
实验平台的采样周期为50 μs,实验电机以转轴相连的方式拖动负载电机,负载电机的三相电流经过二极管不控整流后流经功率电阻。通过手动控制的开关可以切换功率电阻的通断,模拟突增转矩负载的工作状况,从而验证MPFCC方法的动态性能和抗干扰能力。实物实验中d轴电流参考值为0,q轴电流参考值由速度环PI控制器给出,PI控制器参数与仿真中一致。
将所提出的MFPCC方法与有参数MPCC进行对比,令有参数MPCC方法的预测方程中Ld=22 mH、Lq=29 mH、ψf=0.14 Wb,均比真实值偏小约30%以模拟参数失配的情况,在以360 r/min的速度带负载稳态运行时,两种控制方法的性能对比如图4所示。
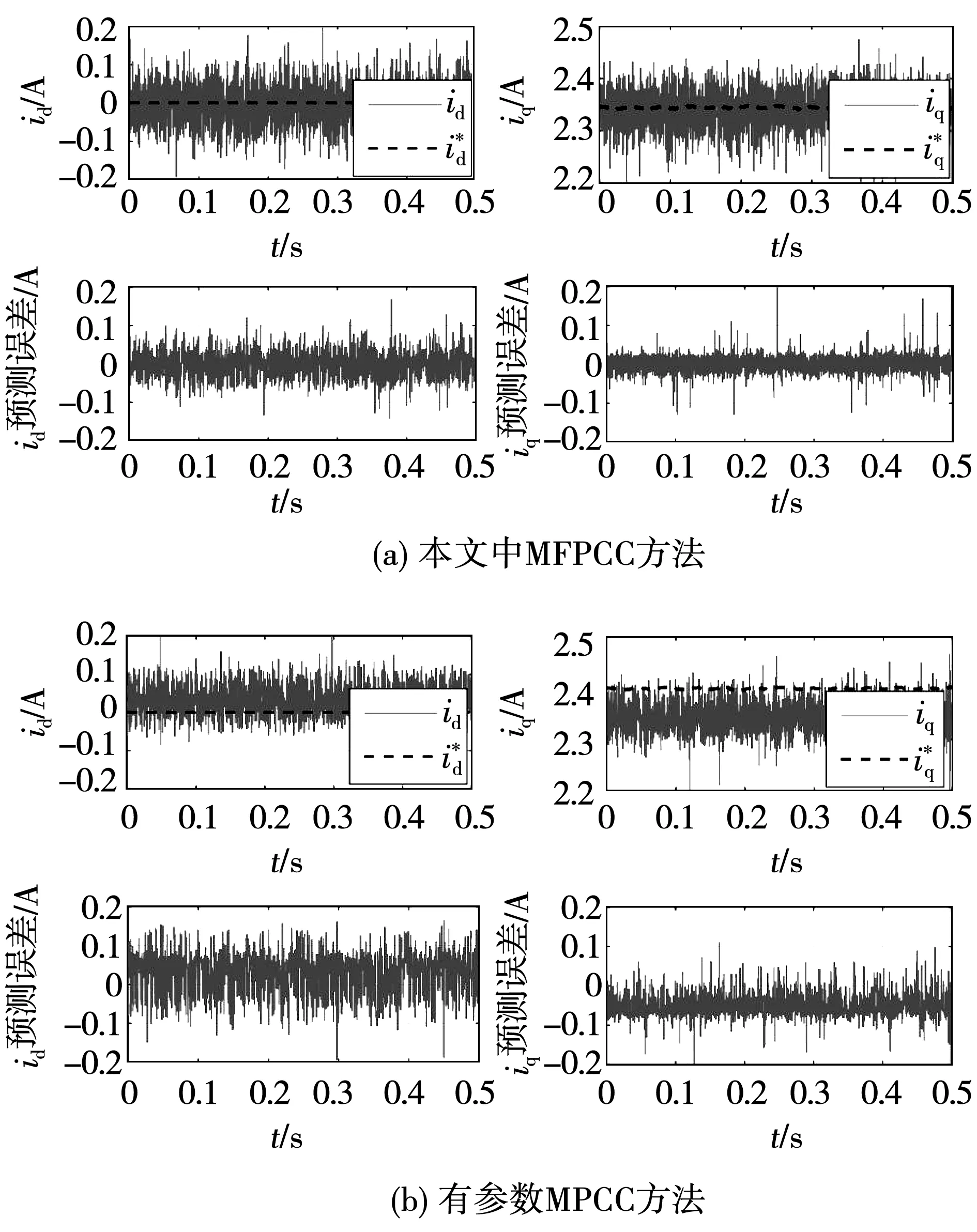
图4 本文中MFPCC与有参数MPCC稳态性能比较Fig.4 Comparison of static performance between proposed MFPCC and traditional MPCC
图4中,有参数MPCC方法中d-q轴电流的参考值与真实值之间均存在误差,并且Ld的控制误差更为显著。将MPCC方法的控制参数代入式(4)中,计算得到的稳态控制误差数值与图中的结果一致,说明MPCC方法的参数失配问题是稳态控制误差的成因,参数失配时MPCC方法的控制效果不够理想。本文提出的MFPCC方法中id、iq均消除了稳态的预测误差,并且预测误差的幅值保持在更小的范围内,预测精确度和稳态控制效果均优于存在参数失配的MPCC方法。

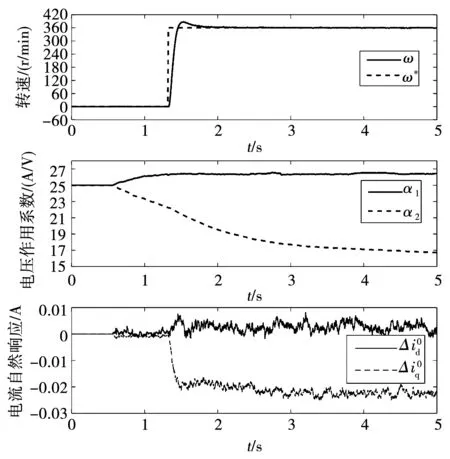
图5 电机启动时参数辨识过程Fig.5 Parameter identification process when PMSM starts
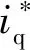
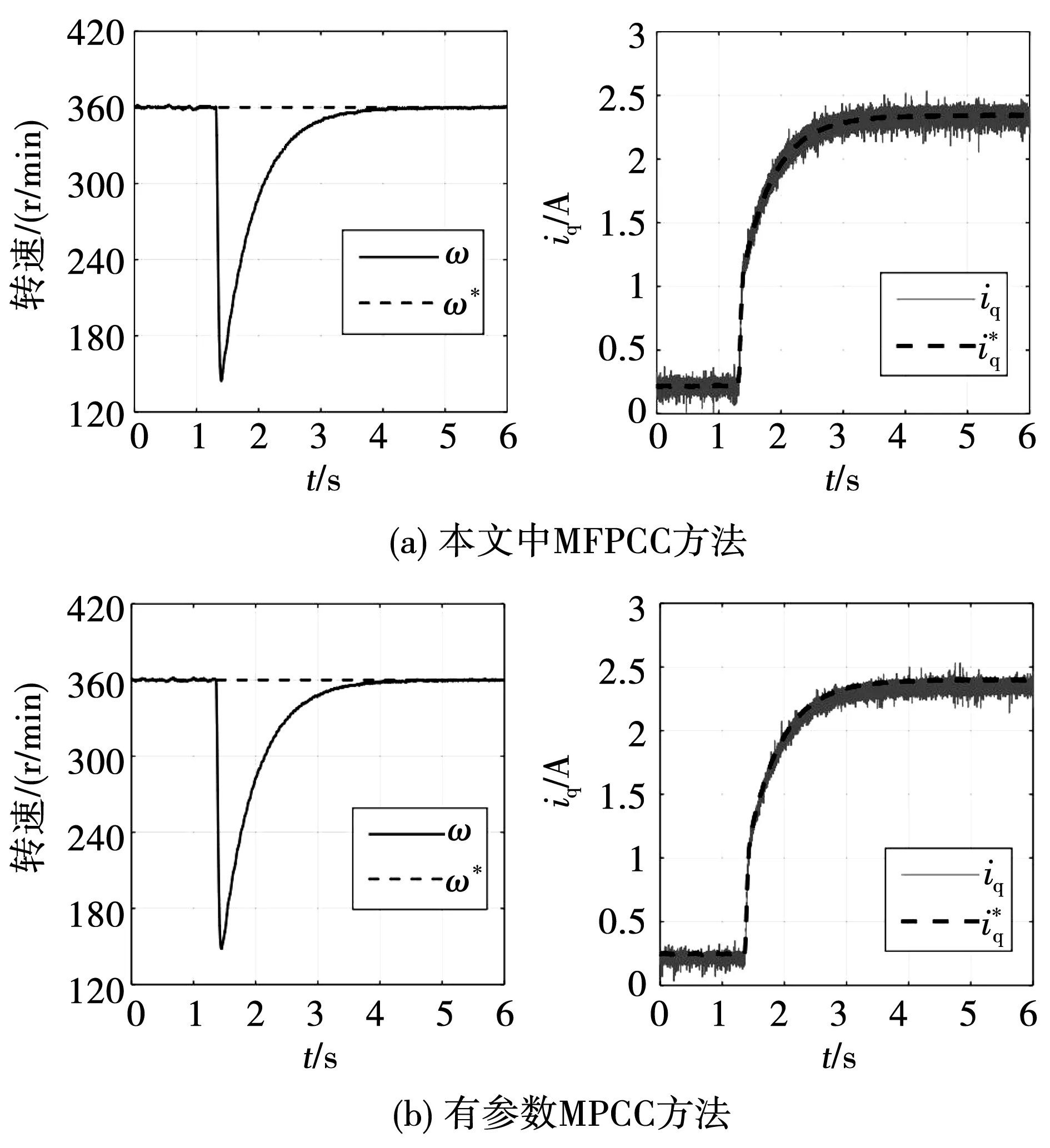
图6 本文中MFPCC与有参数MPCC动态性能比较Fig.6 Comparison of dynamic performance between proposed MFPCC and traditional MPCC
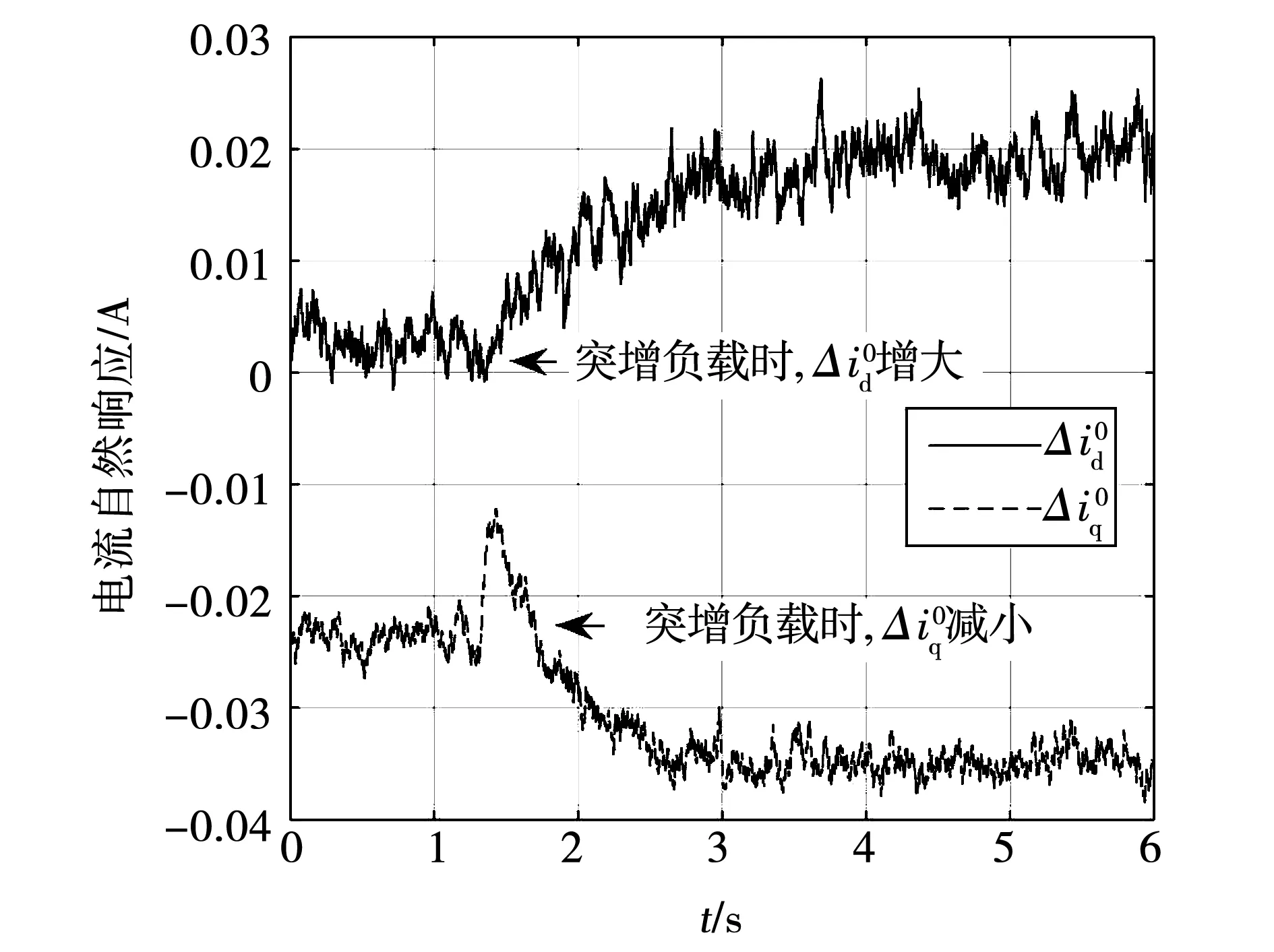
图7 突增负载时电流自然响应的变化Fig.7 Variation of current natural response when increasing motor load
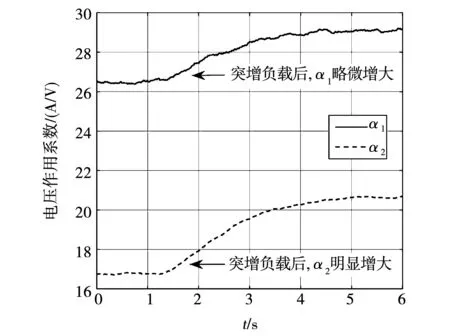
图8 突增负载时电压作用系数的变化Fig.8 Variation of voltage scaling factor when increasing motor load
图8中,α1、α2在增加负载后均变大,其中α2的增大幅度更为明显。由理论分析部分的式(6)可知,α1、α2的数值分别与d-q轴动态电感成反比例,突增负载后iq增大,饱和效应使得lq减小、α2增大;同时由于d-q轴磁路间存在交叉耦合,α1也略微增大。突增负载时电压作用系数的变化与理论分析相符,并且在动态过程中也保持了稳定的观测结果。
5 结 论
本文提出了一种基于超局部模型的永磁电机无参数模型预测方法,解决了有参数MPCC方法的模型失配问题,并且相比于以往研究中提出的MFPCC方法具有更高的稳定性和抗干扰能力。仿真与实验结果证明,电流自然响应的观测量能够真实反映电机的运行状态,在动态过程中也能快速跟踪电机状态的变化;电压作用系数观测器稳定度高,能够消除饱和效应和交叉耦合效应的影响。对比实验证明,本文提出的MFPCC方法的动静态性能优于参数失配的有参数MPCC方法。本方法使用的超局部电流模型也适用于其它类型的电机,具有广泛的应用范围。
