多角度把握学情,以学定教
——以“三角形的认识”的教学实践为例
2021-08-27江苏省南京市江宁区龙都中心小学
江苏省南京市江宁区龙都中心小学 张 勇
卢梭在《爱弥儿》中说道:教育要适应自然,这里的自然指的是儿童身心发展的内在秩序和结构。良好的教育必须依照自然法则进行。新课标要求以学生为主体,面向全体学生、关注学生,那么教师在授课过程中就要了解学生,了解学生的年龄特点、知识水平、接受能力等,如此才能更好地做到因材施教,才能设计出科学合理、切实可行的教学设计。
一、教学前测,找准学生的起点
现代教学论认为:学习者的学习需要是教学活动的出发点和落脚点。所以,教师的教学设计要从分析学情开始。前测法指的是教师根据教学内容设计前测试题,以了解学生在学习该内容之前的认知起点、已有知识经验,判断学生是否具有学习新知识的知识基础。
1.问题设计
教师在执教苏教版“三角形的认识”一课前,就根据教学目标设计了前测题目(见图1)。
学生认识“三角形”吗?了解到什么程度?关于 “三角形”学生还知道什么?这是教学前教师必须探明的问题。以上问题,试图了解学生对“三角形”的认知水平:水平1是对学生“三角形”的图形表征的了解;水平2是对学生对三角形的经验的调查;水平3是了解学生是否会画三角形高的情况的调查。
2.调查结果
学生对“三角形”的认知水平的调查结果显示:水平1:95%的学生能够判断出图1中的①、③、④是三角形;17%的学生认为图1中的⑤也是三角形。水平2:40%的学生对三角形的“边”有所认识;20%的学生提到三角形的“高”;15%的学生能描述三角形的“底”;22%的学生对三角形的“内角和”有了解。水平3:96%的学生能正确画出锐角三角形的高;50%的学生能正确画出直角三角形的高;77%的学生能正确画出钝角三角形的高。
3.前测分析
大部分学生对三角形已经有了一些较为直观的认识,并不是“零基础”。具体表现在:(1)认识边;(2)知道底,想研究底;(3)认识高,想学习高的画法。但是经过与学生的访谈,发现学生们认为的“知道”,只不过是听说过或者只是简单的了解,并没有真正理解这些概念。
部分学生对三角形的高还比较熟悉,超过半数的学生能画出三角形的一条高。主要是因为学生在之前学习“点到直线的距离”和“平行四边形的认识”中积累了一些经验,他们在前测的画高过程中将这些已有的基础进行了迁移。不过,他们并未掌握直角三角形和钝角三角形中特殊高的画法,这一学情就为教师提供了教学方向。
总而言之,大部分的学生对三角形的画法和三角形高的一般画法都表现出“饱”的状态,但对直角三角形中直角边的高以及钝角三角形中特殊高的画法呈现出一种“渴”的状态。
二、教学实践,为学生释疑解惑
基于以上认识,教师重点设计了以下一些教学环节。
1.在描述画法中概括定义
经历在前测中“找一找三角形”的过程以及回忆“在哪些地方见过三角形”的学习活动之后,教师让学生尝试着“画一画三角形”,再分享画三角形的步骤。在描述画图的过程中逐步引导学生根据操作经验概括出三角形的定义。
师:在同学们画三角形的过程中,老师挑选了几幅作品,我们一起来欣赏一下。
师(出示生1的作品):你能跟大家介绍一下你是怎样画的吗?
生1:我先画了一条线,再在这条线的一端画第二条线,最后把两端连接起来,就成了一个三角形。
师:大家觉得他的描述怎么样?
生2:他描述的不是线,应该是线段。
师:那谁愿意再来介绍一下呢?
生3:先画出一条线段,在其中的一个端点处画第二条线段,然后把两个端点连接起来,就能画出一个三角形。
师:谁能描述得更简洁一些呢?
生4:把三条线段接起来就是三角形。
生5:把三条线段连起来就是三角形。
师:大家说的“连”和“接”在数学上就是“围”。三角形是由三条线段“围”成的图形。
【解读】本环节,教师首先引导学生充分感受生活中的三角形,让他们获得对三角形特征的感知,进而形成正确而清晰的表象。接着引导学生画一画三角形,让学生经历利用表象进行操作的过程,去体味三角形形成过程中的共性,并逐步剔除非本质属性,概括出三角形概念的本质属性。此环节的教学真正抓住了学生的学习起点,突出引导学生对三角形特征的理解。
2.在辨析中理解三角形的高
在认识三角形高的定义之后引导学生尝试画出三个三角形(锐角三角形、直角三角形、钝角三角形)的高,再利用生成的错误资源引导学生质疑问难、释疑解惑,最后在思维碰撞中掌握高的画法。
师:我们已经认识了三角形的高,那你会画三角形的高吗?
(学生画高,教师巡视并收集学生作品)
师:老师挑选了几个同学的作品(见图2),大家一起来看一看吧。
生1:这个同学画得不对。虽然他是从一个顶点出发向对边画了一条垂线,但是他的顶点找错了。
生2:因为图中已经标出了底,所以我们应该从这条底相对的顶点出发画对边(底)的垂线(见图3)。
师(小结):我们在画高的时候要注意顶点、底、高必须是对应的。
师:还有同学是这样画高的(见图4)。
生:这条高画得不对,没有从三角形的顶点出发。
师:你能来试着画一画吗?大家有什么发现?
生:我发现这条高和三角形的一条直角边重合了(见图5)。
师(小结):是的,直角三角形的两条直角边是互为底和高的。遇到这种情况,我们可以直接标记“∟”符号即可。
师:再来看看下面一位同学画的高(见图6)。
生1:这条高画得不对,顶点找得不对。
师:你能来试一试吗?
生1:我画不出来,底边不够长。
生2:我来试一试吧。我们可以先把这条底边延长一下,然后再从这条边相对的顶点出发画一条垂直线段,标上垂直符号(见图7)。
师(小结示范图7):先将三角尺的一条直角边与底重合,然后沿着底推动三角尺,另一条直角边经过顶点时,从顶点到底画一条虚线,最后标上直角符号。
【解读】三角形底边上的高就是与底边相对的顶点到底边的垂直线段,因为这部分内容学生在认识三角形的高时已经有所了解,所以在探索画高的方法时,教师没有作过多的引导,而是让学生自己去探索,通过不断地分析错误资源,逐步让学生明晰画高的注意事项,并自主归纳出画高的方法。
三、教学后测,诊断学生思维
教学后测的目的是通过学生学习信息的反馈,了解教师的教学效果,为再次教学提供改进建议,促进教师专业水平的不断提升。后测调查一般将前测调查的学生作为对象,后测的内容、形式、难度、时间也要与前测基本保持一致,这样便于作前后测的对比分析。 在教学“三角形认识”时,教师便进行如下问卷调查。
1.后测试题
对之前参与前测的学生进行后测(见图8),了解教学后学生关于“三角形”的知识掌握程度。
三种水平基本与前测题型一致、难度相当,能够反映学生对角的概念理解和应用情况。
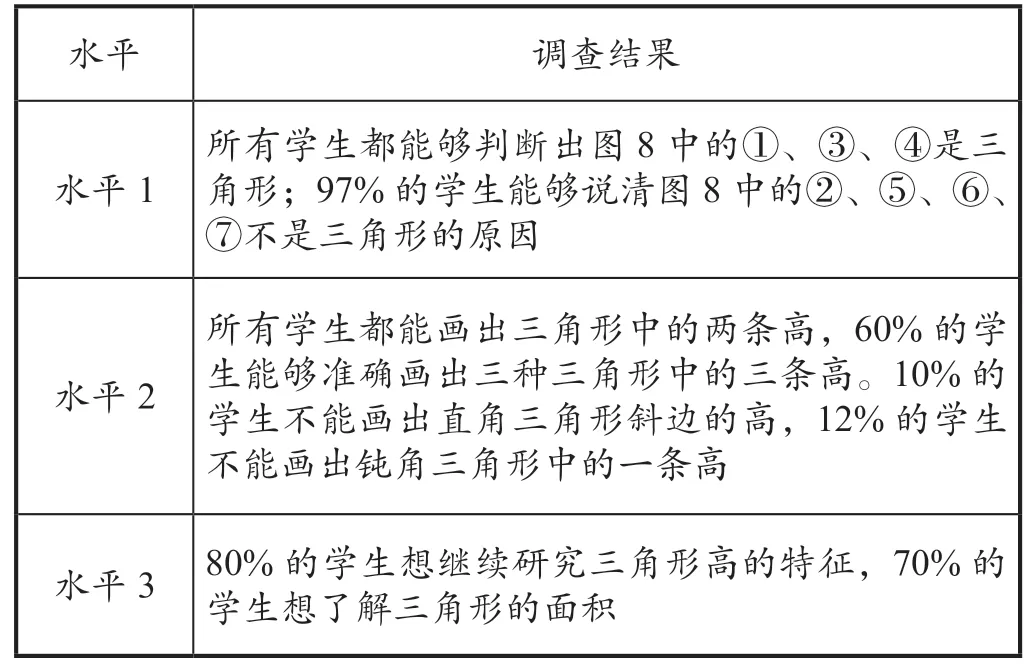
2.调查结果
?
3.调查分析
绝大多数学生能够准确地进行三角形的图像表征,并能够根据三角形的特征说明不是三角形的原因。说明绝大部分学生已经形成对三角形的清晰表象,并能够明晰三角形的特征。
绝大部分学生都能够准确画出三角中对应底的高,说明大多数学生掌握了高的定义和画法。超过半数的学生能够画出三角形中的三条高,说明这部分学生已经完全掌握三角形高的定义,并能够根据高的定义画出三角形中所有的高。
80%的学生想继续研究三角形高的特征,说明这部分学生理解了三角形高的定义,体会到三角形的高的特征远不止我们今天课堂上所研究的;70%的学生想了解三角形的面积,体现了学生对于三角形这种图形的研究兴趣。
学情分析是有效课堂的铺路石。教师只有准确进行学情分析才会预设全面、周到,才会做到因材施教、因人施教、因情设教,课堂生成才会顺畅、高效。
