在数学课堂中提升学生问题发现力的策略探究

摘 要：在教学中，教师要想培养学生的数学学科素养，就要提升学生的问题发现力。教师应结合教材内容，以生为本， 在日常教学中尝试应用相应的策略与方案。笔者从教学现状入手，分析在教学过程中提升学生问题发现力的重要性，研究在教学过程中如何有效地运用策略，来调动发学生发现问题的积极性，进而提升学生的问题发现力，以期通过提升学生问题发现力来提升学生的数学核心素养。

关键词：初中数学;问题发现力;问题式教学;教学策略

中图分类号：G420                       文献标识码：A                    文章编号：2095-624X（2021）02-0074-03

引 言

《义务教育数学课程标准（2011年版）》对学生提出“四能”的要求，即发现问题、提出问题、分析问题、解决问题的能力[1]，其中最根本的是学生“发现问题”的能力。因而，根据具体的数学教学内容，科学、合理地为学生提出数学问题，促使学生树立问题意识并学会提出问题，是教师教学设计中首先要解决的问题。本文将结合教学实际，谈谈笔者在这方面的一些思考和实践。

一、培养学生问题发现力存在的问题

数学学习过程本身就是一个探究式的过程，要求学生不断地提出问题，并且不断地思考，寻找有效方法解决数学问题。在这一数学学习过程中，学生的问题发现力起着关键作用。若学生的问题发现力比较薄弱，学生就很难发现数学知识中蕴含的数学问题，也就很难提出有效的数学问题来进行思考与探究学习。纵观当前的数学教学，我们发现其存在以下一些问题。

（1）教师的数学问题意识比较薄弱。教师在开展数学教学活动时，疏忽了对学生数学问题意识的培养，更多的是通过直接提问来展开问题式探究教学活动，不利于学生自主发现数学教学中的数学问题。

（2）学生的自主学习意识比较薄弱。学生的问题发现力在一定程度上要依靠其自主学习能力。若学生的自主学习意识薄弱，学生就难以发挥学习积极性进行自主学习。这在一定程度上阻碍了学生数学问题发现能力的有效提升。

（3）教学活动机械性强，学生的问题发现能力没有得到重视，缺乏良好的数学问题探究学习环境。

二、提升学生问题发现力的重要性

学生发现问题能力的强弱，在一定程度上也体现出学生数学知识应用意识及创造力的高低。学生的数学应用意识与创造力，是新课程改革提出的培养目标。在数学课堂教学中，教师应采用有效的教学策略，提升学生的问题发现能力。

（一）锻炼学生的思维能力

基于提升学生问题发现能力的教学策略，教师要有意识地创设能让学生产生探究欲望的问题情境。在形成问题意识的过程中，学生思维活跃度高，可以有效锻炼自身的数学思维能力。

（二）增强学生的学习专注力

教师在围绕数学教学内容来培养学生良好的问题发现力时，学生需要集中精神。这样才可以让学生进行高效的思维活动，保证学生对数学知识的探究热情和探究效果。

（三）调动学生的学习积极性

学生的学习积极性在很大程度上关系到学生数学学习的质量，也关系到问题探究活动的质量。学生提高问题发现力，就能在数学学习中发现问题，从而调动学生学习积极性，使其自主探究和解决问题。

基于此，笔者提出在数学课堂中提升学生问题发现力的策略。

三、提升学生问题发现力的策略

为完成提升学生的问题发现力这一重要的教学任务，笔者依托教材内容，开发适合提升学生问题发现力的素材，精心设计教学的各个环节，激发学生对问题的探究兴趣，培养学生自主探究和发现数学问题的热情。

（一）源于数学史料发现数学问题

教师应加强对数学文化的渗透和运用，让学生产生挖掘数学知识中蕴含的问题的兴趣。

【案例1】以“实数的引入”为例

在“实数的引入”一课教学中，教师可以让学生在课前通过查阅资料了解实数的概念，并组建数学学习小组探讨相关问题，通过合作形成诸如PPT的报告，在课堂上汇报展示，同时其他小组可以根据该小组的展示内容进行提问。在实际教学活动中，笔者发现，学生向同学提问的积极性非常高，以提出和回答问题为荣，提升了“第一个发现无理数的人是谁”“无理数和有理数有什么区别”“无理数能不能在数軸上表示以及如何表示”等数学问题。通过这次教学活动，学生不仅了解了所学知识的背景，还明白了“真理是不可战胜的”。此外，学生也感受到了数学学习要勇于思考、大胆质疑，从而提高自身对问题的发现能力。

数学史料的内容丰富多彩，包括数学家的生平、奇闻逸事，数学知识的进程与完善，数学思想的起源与发展等。这些数学史料渗透了数学文化，激发了学生发现数学问题的积极性。

（二）基于自主操作发现数学问题

教育家皮亚杰说过：“知识来源于动作，而非源于物体。”由此可见，知识的习得要通过学生的自主操作。教师在教学中要给学生留出足够的时间和空间去经历探究的过程，使其积累活动经验，进而更自主、有效地发现问题、提出问题。

【案例2】以“图形的轴对称”为例

笔者给学生展示了一组图形，如图1所示。

师：观察以上图形，你可以提出与对称图形、对称轴、对称点有关的数学问题吗？

（1）学生先独立思考，然后小组讨论，组长统计提出的问题。

（2）交流、整理问题。学生发现的问题：①这些图形都是轴对称图形吗？②它们分别有几条对称轴？③怎么找对称点？④对称点与对称轴之间有什么关系？（教师可以给予适当提示）

（3）解决问题。归纳得出轴对称图形的性质：对称轴垂直平分连接两个对称点的线段。

（4）验证轴对称图形的性质。笔者呈现与对称有关的几何图形，通过提出问题的形式，引导学生巩固轴对称图形的概念和对称轴、对称点的概念，探索对称轴与对称点的关系，让学生进行动手实践、观察思考、提问交流、归纳总结轴对称图形的性质。这样的自主操作活动既调动了学生的学习积极性，又提升了学生的数学问题发现力，对提高学生的数学素养有着积极的促进意义。

（三）基于生活情境发现数学问题

【案例3】以“图形的轴对称”为例

师：有两个村庄A、B和一条笔直的马路，要在马路上修建一座加油站，你们可以提出哪些数学问题？

生1：A村与B村在马路的同侧还是异侧？

生2：加油站建在哪里与A村最近？加油站建在哪里与B村最近？

生3：加油站建在哪里到A村与到B村的距离之和最小？

生4：加油站建在哪里到A村与到B村的距离之差最大？

笔者创设实际生活问题情境，激起学生提问的兴趣与积极性，培养了学生的数学问题发现力。学生在解决问题的过程中，理解了利用轴对称图形的性质解决生活问题的知识难点。

（四）鉴于开放编题，发现数学问题

【案例4】以“一次函数”复习课为例

师：观察图象（见图2），你可以提出哪些问题？

生1：求直线AB的解析式。

生2：求直线AB与坐标轴交点的横坐标。

生3：当x>0时，求y的取值范围;当y>0时，求x的取值范围。

生4：函数图象的增减性是怎样的？经过了哪些象限？

生5：求线段AB的长度。

生6：y轴上有一点C（0，-1），求?ABC的面积。

……

师：在原图的基础上再加一条直线PQ（见图3），你还可以提出哪些问题？

生1：求直线PQ的解析式。

生2：求直线AB与直线PQ交点的坐标。

生3：记直线AB为y1，记直线PQ为y2，当x取何值时，满足y1>y2，且y1≤y2？

生4：求?CQG的面积。

生5：在x轴上有一点M，求PM+GM的最小值。

生6：若在y轴上有一点R，当?PQR为等腰三角形时，求点R的坐标。

笔者只给出开放性的条件，让学生通过观察已给图象，激发了自身的联想和数学问题发现能力，以小组合作的形式提出问题、归纳问题、解决问题，活跃了自身的思维，提升了问题发现能力。

（五）依于媒体技术发现数学问题

多媒体技术的辅助教学也可以提升学生的数学问题发现力。教师要发挥多媒体技术的教学优势，激发学生对数学问题的探究动力。例如，教师在课堂上利用多媒体技术设备来播放相应的教学视频或图片，让学生自主对直观形象的内容进行观察，然后发现其中蕴含的数学问题;也可以利用几何画板、GeoGebra等动态软件演示数学问题，提升学生的问题发现力。

【案例5】

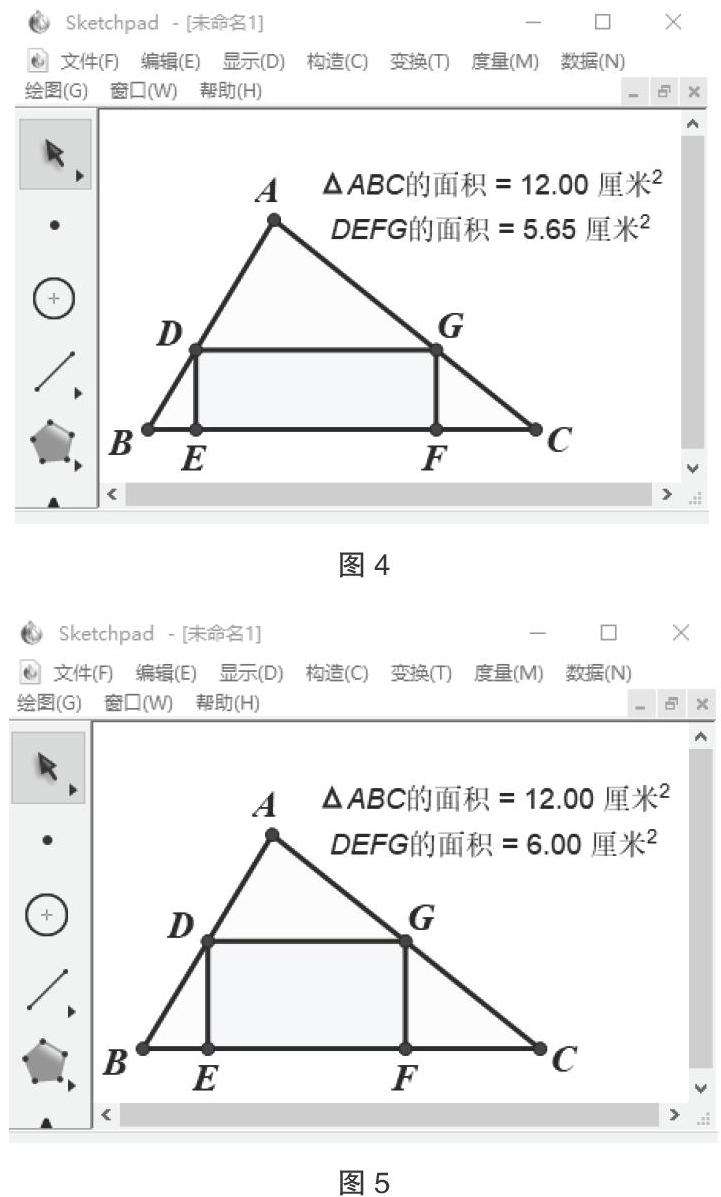
已知?ABC的面积为12cm2，D是边BC上一动点，矩形DEFG内接于?ABC，其中点E、F在边AC上，点G在边AB上。教师利用几何画板制作课件，拖动D点，使矩形DEFG形状发生变化，在变化过程中引导学生提出数学问题（见图4、图5）。

生1：若AC=5，求边AC上的高。

生2：若D是边AB中点，求矩形DEFG的面积。

生3：当点D在边BC上运动时，矩形DEFG的面积是否有最大值？如果有，什么时候面积最大？最大面积是多少？如果没有，请说明理由。

生4：当矩形面积最大时，与三角形面积存在怎样的关系？

多媒体技术辅助下开展的数学教学活动，不仅可以很好地展现数学的动态变化过程，有效激发学生的学习兴趣，还能提升学生在研究数学问题时的发现能力。

结 语

经过对“提升学生问题发现能力”的探索与实践，笔者坚持在教学过程中以问题为导向，以提高核心素养为目的，围绕数学问题发现力来优化数学教学過程，保障数学教学的有效性。以上策略的实施，使数学课堂更有活力，学生学习数学的兴趣更浓了，学生的数学思维得到了充分的锻炼，学生的问题发现能力有了很大的提升。同时，笔者在实施策略过程中也有几个值得注意的问题，争取在以后的教学中不断改进。

（1）开放性编题的方向。教师一旦放开问题方向，学生可能会跑偏，有时会出现课堂时间不够用的问题。这就需要教师在进行教学设计时更精细，预设更充分。

（2）多媒体技术的学习。除日常教学用的PPT外，教师还要去学习几何画板、GeoGebra等数学软件，优化现代化教学模式，做到精准施教，以便于学生探究数学问题、提升问题发现能力。

（3）学生问题的利用。随着学生问题发现能力的提高，学生会提出很多有价值、有意义的数学问题。教师要对其进行优化整合，生成教学资源，更好地指导教学实践。

[参考文献]

中华人民共和国教育部.义务教育数学课程标准 （2011年版）[S].北京：北京师范大学出版社，2012.

作者简介：陈建芳（1980.10—），女，浙江杭州人，本科学历，一级教师。