基于联合优化的高通量卫星跳波束图案设计研究

张 晨，彭明阳，张更新

1.南京邮电大学 通信与信息工程学院，江苏 南京 210003

2.南京邮电大学 通信与网络技术国家工程研究中心，江苏 南京 210003

近年来随着天地一体化信息网络的蓬勃发展，卫星通信所承载的业务发生了显著变化，从语音通话、低速率数据业务转变为高速率的宽带互联网接入、移动多媒体业务。在此背景下，高通量卫星（High-Throughput Satellite，HTS）应运而生，通过借鉴陆地无线蜂窝通信系统的频率复用和多点波束技术，在相同可用频谱资源的条件下可提高数倍通信容量，由此将卫星通信带入到高通量发展阶段。

在传统的高通量卫星系统中，各波束所分配的系统资源相对固定。然而系统所服务的用户业务类型差异较大，业务分布的时变性和空间不均匀性显著。这将会导致系统资源的浪费和波束的忙闲不均，进一步引起资源的碎片化配置。对此，业界提出一种基于时间分片的跳波束（Beam-Hopping，BH）技术［1］，在同一时刻只有其中的部分波束激活工作，以业务需求为驱动，灵活地分配系统资源，达到随需覆盖，同时大幅度提高系统资源率，提升系统吞吐量。跳波束技术迅速得到了业界的广泛关注，而其资源分配和图案设计作为跳波束的核心迅速成为研究热点。以欧洲区域卫星宽带业务分布为系统需求，文献［2］对比了Ka频段通信卫星中采用和不采用跳波束技术的系统性能，证明了跳波束技术能够大幅度提高系统实际容量。文献［3－7］建立了跳波束系统中资源分配的初步数学模型，并分别利用启发式算法和神经网络等方法，提高了前向下行链路的吞吐量。此外，文献［8］除了时隙分配外，分别采用二分法和迭代算法对功率和频谱资源进行了优化分配。文献［9－10］分别建立了最小化同频干扰和最大化信干噪比的跳波束资源分配目标函数，并对跳波束图案做了初步设计。在此基础上，文献［11］提出一种基于分簇的全频带跳波束图案优化方法，降低了同频干扰和波束的频繁切换。文献［12］探讨了跳波束技术应用到低轨卫星星座场景的适配性，并给出初步的时隙分配方案。文献［13］利用机器学习算法，探讨了星载转发器在处理转发模式下，数据包的时延优化问题。

然而现有文献大多在控制和业务相分离的场景下，研究跳波束资源分配及图案设计。也就是卫星载荷需单独配置宽波束，用于控制信令的传输。然而实际系统中还存在控制随业务波束的场景，卫星载荷并没有配置承载控制信令的宽波束。所以现有的算法难以发挥出跳波束的优势，不可避免面临着波束间断带来的系统同步问题，以及同频干扰引起的信号质量恶化。

为解决以上问题，针对控制随业务波束的场景，在作者之前的初步工作基础上［14］，本文提出一种联合优化的跳波束图案设计方法。首先建立跳波束时隙分配模型，通过凸优化算法得到各波束分配的跳波束时隙个数，尽可能地满足各波束的业务需求；然后综合考虑同频干扰、系统同步等因素，引入同频复用距离、波束重访时间、最大同步保持时间等限制条件对时隙分配结果进行联合优化，确定各波束的驻留时间和次序，从而得到波束跳跃图案。仿真结果表明，相比于传统方法，本文提出的跳波束图案设计方法，能够有效地消除系统内部同频干扰，兼顾系统同步，大幅度提高系统容量。并且进一步仿真了业务动态分布不均的情况，结果同样表明本文所提算法相较传统多波束资源分配，更加能够满足业务分布不均性。本文的主要贡献在于：首先，针对控制随业务波束的场景下缺乏有效的跳波束图案设计方法的问题，以联合优化为设计思路，建立了该场景下的数学优化模型；其次，通过波束重访时间和同频复用距离限制条件，分别解决了波束间断带来的同步问题和全频复用导致的同频干扰问题；最后，对业务分布的离散性进行量化建模，进一步验证了本文所提算法在不同业务分布情况下的有效性。

1 系统模型

1.1 跳波束前向链路模型

如图1所示，跳波束卫星系统由网络控制中心、信关站、配备跳波束控制器的卫星和用户终端组成。其中前向链路（信关站到用户终端），采用兼容DVBS2／S2X协议［15－16］的跳波束工作方式，具体如下：

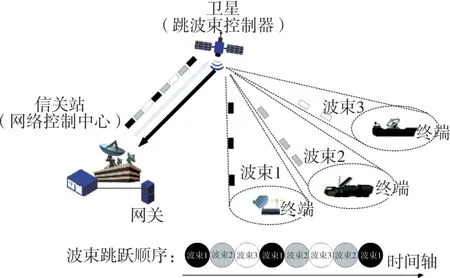
图1 跳波束系统前向链路

（1）网控控制中心除生成常规的控制信令外，还要根据各用户的业务需求进行资源分配，生成跳波束时间计划信令；

（2）信关站将业务信息和控制信令以TDM方式发送给卫星；

（3）星载跳波束控制器通过解调跳波束控制指令，实现卫星上波束的同步跳变，将不同的数据流切换至不同的波束；

（4）用户终端在波束驻留时间内完成业务的传输和信令交互。

如前文所述，在本文关注的场景中，星上没有额外配置宽波束天线用于形成全球波束来传输控制信令，也就是说控制信令必须随业务波束进行交互，其优势在于降低了星载设备量，并且控制信令不易截获或干扰。但对跳波束图案的设计提出了较高的要求，这也是本文研究的出发点。

假设卫星配置了M个业务波束，每个点波束的覆盖区域称为波位（Beam Position），波束和相应波位一一对应。为便于分析问题、阐述原理，采用平均分簇的原则，每b个波束分为一个波束簇（Beam Cluster），共C＝M/b个簇。同一时刻，每个簇内只有一个波束被激活工作，也就是共C个波束同时点亮。在传统的多载波、多波束卫星通信系统中，所有波束都同时工作，且系统的频谱、功率等资源平均或固化比例分配给各个波束，无法根据业务需求进行动态调制，无疑造成各波束之间资源的浪费和紧缺。另一方面由于卫星转发器工作在多载波模式下，存在功率回退线性，会导致功率资源利用率的进一步下降。因此，跳波束系统采用时间分片技术，将星上的功率、带宽等资源池化，各波束可共享系统的全部资源，根据各波位内用户的业务需求，动态调整资源分配，进行按需覆盖的服务，提高了资源利用效率；同时前向链路工作在单载波模式，进一步避免了功率回退的损失。

1.2 跳波束时隙分配模型

图2是跳波束时隙分配模型图，具体参数［7］如下：

图2 跳波束时隙分配模型

（1）跳波束时隙Ts：指的是分配给一个波束的最小持续时间。可根据用户业务需求量或QoS，动态分配给各波束相应的时隙个数。

（2）跳波束周期W：也可称为跳波束时间窗口。DVB-S2X协议附录E中推荐的时间窗口长度包含128或256个时隙。实际可根据系统参数和业务需求动态设置窗口长度。

（3）波束重访时间Trv：某个波束所分配的时隙之间的间隔时间。由于业务波束的跳跃会造成物理连接的间断，因此波束重访时间过长，会影响用户终端的同步。

（4）跳波束时间计划表（Beam-Hopping Time Plan，BHTP）：大尺度时间内的跳波束时间分片传输计划，一般包括多个跳波束周期，以及单个时隙的长度、系统带宽、载波频率等参数。跳波束时间计划表要综合考虑用户申请、业务预测、系统能力和现有资源等因素，由网控中心或服务提供商提前生成，并作为控制信令发送给卫星和地面系统。一般对于每个簇，都有各自相应的跳波束时间计划表。

（5）跳波束图案（Beam-Hopping Pattern）：也称作波束跳跃图案。其物理意义在于每个波束在其对应波位上的单次驻留时间和工作次序。跳波束图案设计在跳波束系统中有着重要的意义，因为资源分配算法只能得出各波束的跳波束时隙总数等系统资源分配结果，无法确定各波束在一个跳波束周期中的单次驻留时间和工作顺序。某个波位单次驻留时间太长会影响其他波位的业务服务响应时间，间接影响波束重访时间，从而造成系统同步问题；但如果单次驻留时间太短，又会因为频繁切换降低信息传输效率。而波束的工作顺序，要考虑相邻波束的同频干扰，使得相邻波束在工作时间上错开，同时工作的波束在空间距离上隔离。

由此可见，跳波束图案对系统设计有着重要的作用，这也正是本文的研究切入点。

1.3 同频干扰模型及分析

如前文所述，在跳波束系统中，由于系统资源的池化，每个波束都可利用全部的频谱带宽资源Btot。由此引出两种簇间的频率复用方案：部分频率复用和全频率复用。部分频率复用将总带宽分段，在簇间进行传统的四色或七色频率复用，实际上是以牺牲频谱利用效率为代价来减轻同频干扰。即使进一步叠加极化复用，每个簇中处于工作状态的波束也只能使用部分频带，其频谱效率也远小于全频带复用，更无法发挥跳波束的技术优势。因此，本文采用簇间全频率复用的方案，以最大化利用系统资源，提高吞吐量。然而全频复用就意味着可能带来同频干扰。因此必须对波束干扰进行建模和分析，为后续跳波束图案的联合设计奠定基础。

共信道干扰产生的原因是天线辐射方向图的旁瓣效应，如图3所示，设干扰源波束为n，被干扰波位为m，干扰值主要与卫星到波位m，n中心点瞄准线的夹角θmn有关，下行链路波位间的干扰［11］为

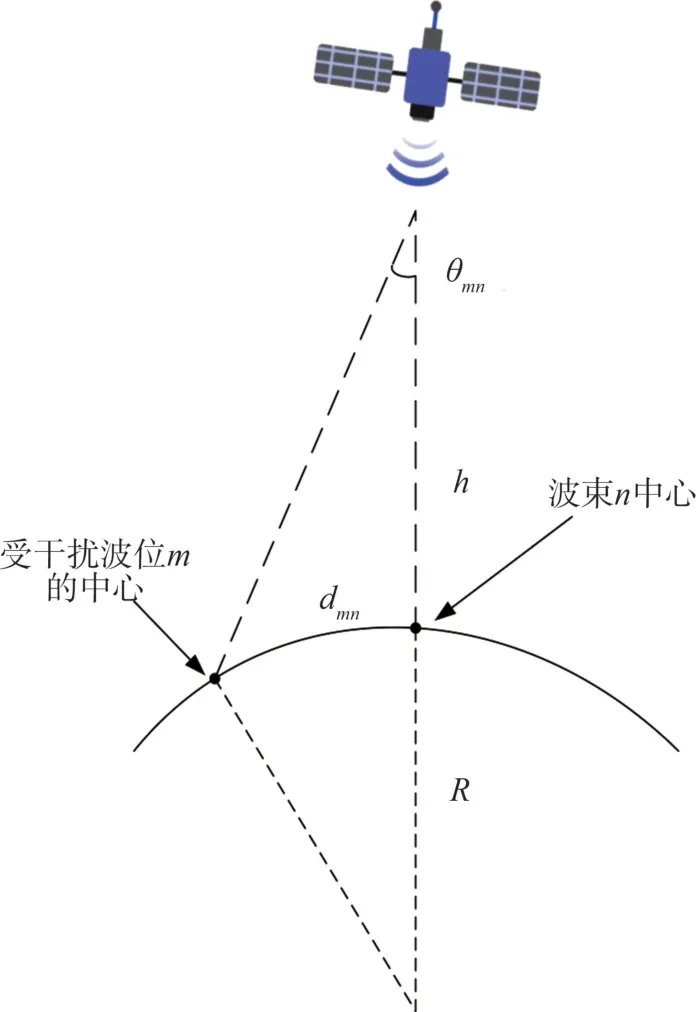
图3 波束间干扰模型

其中，N代表与波位m复用频率相同的小区数目，Pn为卫星对波位n的发射功率，gn为卫星到波位n中心点之间的天线增益，dmn为波位m，n中心点之间的距离，λ为信号波长，Lm（θmn）为卫星到受干扰波位m中心点的信道衰落，Gn（θmn）为覆盖波位n的波束对于波位m中心点的天线增益

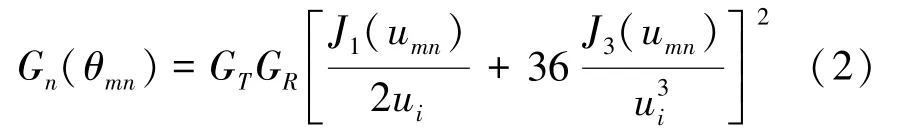
其中，GT代表天线的传输主瓣增益，GR为天线的接收峰值增益，J1（·）和J3（·）为一阶和三阶贝塞尔函数。

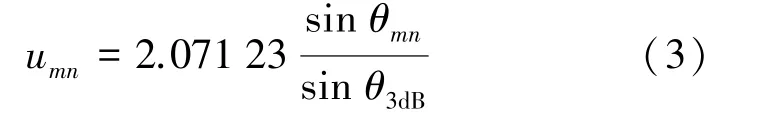
其中，θmn表示信号入射方向与波束中心指向之间的夹角，θ3dB指接收天线的半功率角。

从卫星的角度来讲，干扰值主要与卫星到波位m，n中心点瞄准线的夹角θmn有关［11］

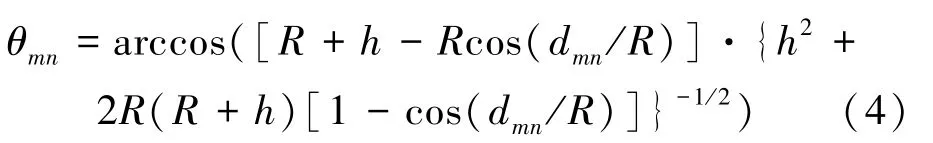
由式（4）可得，当地球半径R和卫星高度h固定时，夹角θmn由两点距离dmn决定。

建立波束间的干扰模型后，可得信干噪比的计算公式为

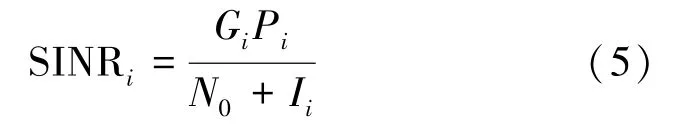
由此可见，波束间同频干扰的大小与波束间的距离密切相关。由文献［11］可知，在高通量卫星DVB-S2协议中，可选取合适的距离门限为4倍波束半径作为频率复用距离。当同频复用的波束距离大于4倍波束半径，可忽略干扰的影响。

2 目标函数与优化方法

2.1 业务驱动的跳波束时隙分配算法

使时隙分配在满足资源限制的基础上达到最优或者次优解，最终使得实际波束分配的容量尽可能达到需求，为此可建立N阶差分目标函数

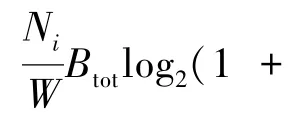
其中，SNRi表示第i个波束的信噪比，公式如下

其中，Gi表示波束i的信道增益，Pi表示第i个波束的卫星发射功率，N0为噪声功率。

其中，GT表示天线的传输增益，GR为天线的接收增益，LSL为自由空间传播损耗，LRA为链路雨衰。将式（10），式（11）逐步代入式（9）中，即可求得各波束的时隙分配数目。

2.2 联合优化的跳波束图案设计方法

在根据业务需求，得到各波束分配的最优或次优时隙个数后，下一步就是对跳波束图案进行联合优化设计，以确定各波束的驻留时间和点亮顺序，最终网控中心根据各簇的跳波束图案（波束跳跃图案）生成跳波束时间计划表BHTP。由此可以看出，跳波束图案关系到整个跳波束系统的工作状态，是关键性的系统参数。

跳波束图案优化设计，需要联合多个波束簇进行跳波束图案协调，本文综合考虑以下关键因素进行联合优化设计：

（1）动态干扰规避措施。如前文所述，以最大化利用系统资源，提高吞吐量为根本目标，充分发挥跳波束技术的优势，本文采用了全频复用方案。然而对于热点区域，业务需求量大且持续时间长，区域内距离相近的波束无法在时隙上错开，同时工作才能满足用户需求。因此在本文的跳波束图案联合优化设计中，必须尽可能使得同时工作的波束之间的距离大于同频复用距离，以避免同频干扰，提高接收信号的信干噪比。尽管干扰规避或抑制的信号处理方法众多，但在综合考虑算法复杂度以及与跳波束资源分配方法的融合度方面，基于距离控制的干扰避免方法，显然较有优势。

（2）波束重访和系统同步。针对控制信令随业务波束的场景，因为没有单独配置广域覆盖的控制波束，用户终端在波束跳跃的过程中，面临着链路连接间断的情况。一旦该用户所在的波束对应的重访时间超过终端的最大同步保持时间，用户就必须重新进行入网和系统同步的过程。根据DVB-S2协议中的注册入网和同步的流程，用户需要系统额外分配多个广播时隙，以S-ALOHA的方式进行竞争接入，严重影响了业务的传输效率和系统吞吐量。因此在本文的跳波束图案设计中，当某个波束的重访时间过长时，必须给该波束分配控制时隙，用于系统的同步，避免出现波束重访时间大于终端最大同步保持时间的情况，导致用户失去同步而退网。极端情况下，即使某个波束内在该跳波束周期内无业务传输的需求，在BHTP表中，也要给该波束分配至少一个控制时隙，用于信令的交互。

（3）波束驻留时间。在满足干扰避免和波束重访的基础上，进一步保证各波位在时隙上的连续性，也就是通过优化尽可能地增大波束的单次驻留时间。传统的跳波束时隙分配算法，采用波束串行分配的方式将资源分配给用户，使得时隙离散化程度较高，导致单次波束驻留时间较短。因此在本文的跳波束联合优化设计中，区别于传统方法，以波束为优化对象分配相应时隙，这种并行分配的方法可以使得跳波束图案中的时隙更加连续［11］，从而增大单次波束驻留时间，避免了频繁切换带来的冗余信令开销，增强了用户的服务体验。

综合以上，本文提出的基于联合优化的跳波束图案设计算法，表示如下。

联合优化跳波束图案设计算法

其中，W表示总时隙个数，N（n）表示分配给波位n的剩余时隙个数，C行W列的矩阵Beam（i，j）用来表示时隙j簇i中正在工作的波位编号。该算法首先按波位的需求大小进行一个预排序，得到波束工作顺序矩阵Beam（i，j），然后引入距离控制，以减小同时工作的各波位间的共信道干扰。τmax表示最大同步保持时间，t（k）表示波位k的未被访问时间，引入距离控制后检查各波位的未被访问时间，超过最大同步保持时间的波位进行一个重访过程。

3 数值仿真与结果分析

3.1 仿真参数

以Ka波段的GEO卫星资源受限系统为仿真场景，下行链路频率30 GHz，共M＝21个波束，平均分为3个簇，每簇7个波束，控制信令随业务波束，卫星不再额外配置宽波束用于信令广播。其他关键的系统参数如表1所示。

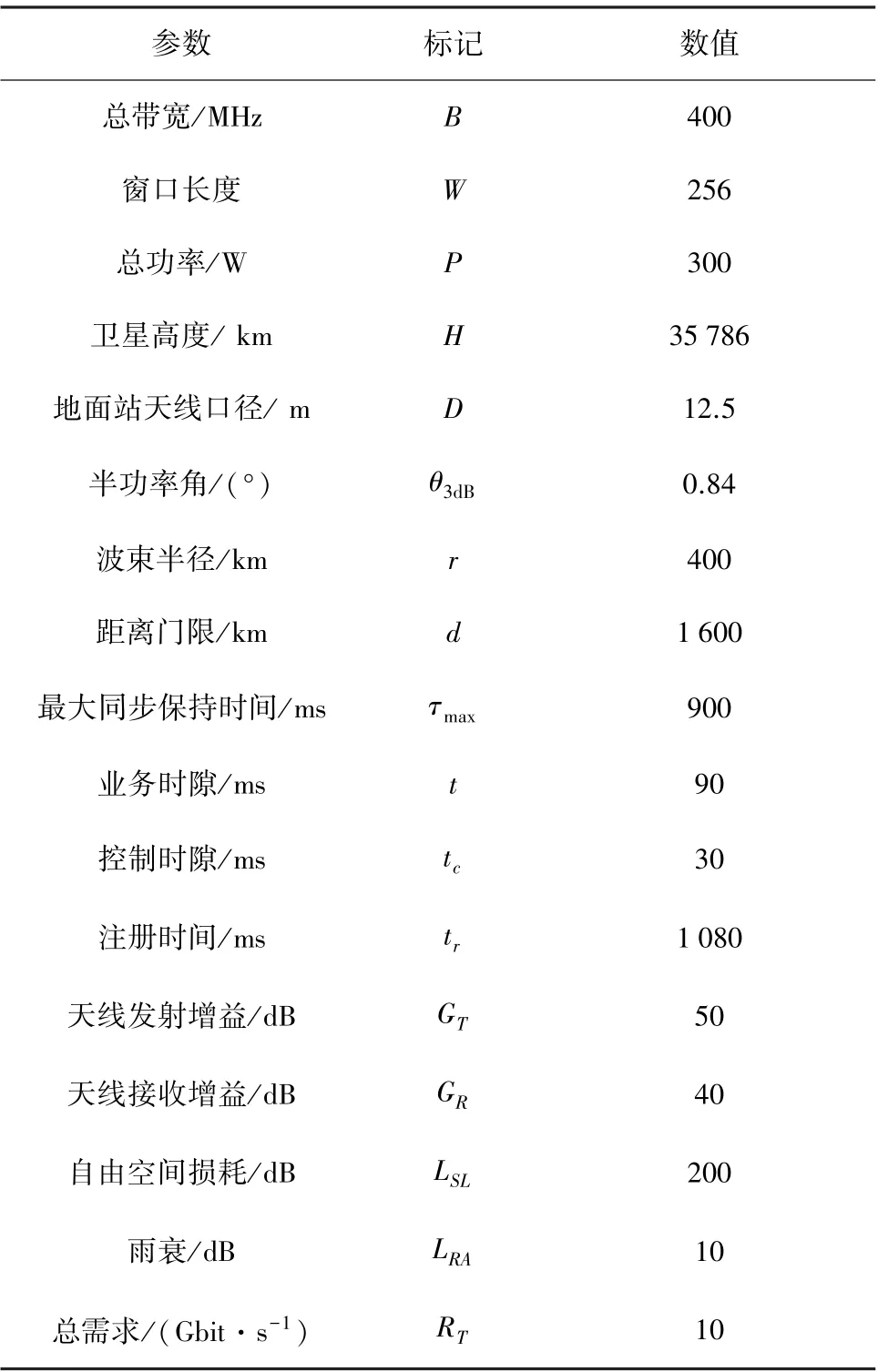
表1 系统主要参数

3.2 结果与分析

在分析仿真结果之前，先引入以下几个参量用于评估系统：

系统实际容量（实际吞吐量）：指的是资源受限场景下，各波束实际分配的容量和请求容量两者的最小值。

业务满意度：系统的实际容量与各波束所需的业务量比值。

业务需求分布不均性：为了描述各波位的业务需求分布特性，定义了一个表征业务不均匀性分布的归一化参数μ，称之为离散系数［18］

其中，ATD（the Aggregate Traffic Demand）为总的业务量需求，SATD为覆盖范围内所有波位的ATD的标准差，MATD为覆盖范围内所有波位的ATD的平均值。

如图4所示，传统的跳波束图案设计方法在全频复用时，没有考虑同频干扰的问题，所以导致波束间干扰显著。而从图5可以看出，本文提出的跳波束图案设计方法因为对同时激活的波束进行了空间距离限制，所以能够有效地避免同频干扰，从而提高用户接收端的信干噪比，增大传输容量。

图4 传统跳波束算法的干扰情况

图5 联合优化算法的干扰情况

另一方面，图6给出了不同算法下，系统的吞吐量仿真图。

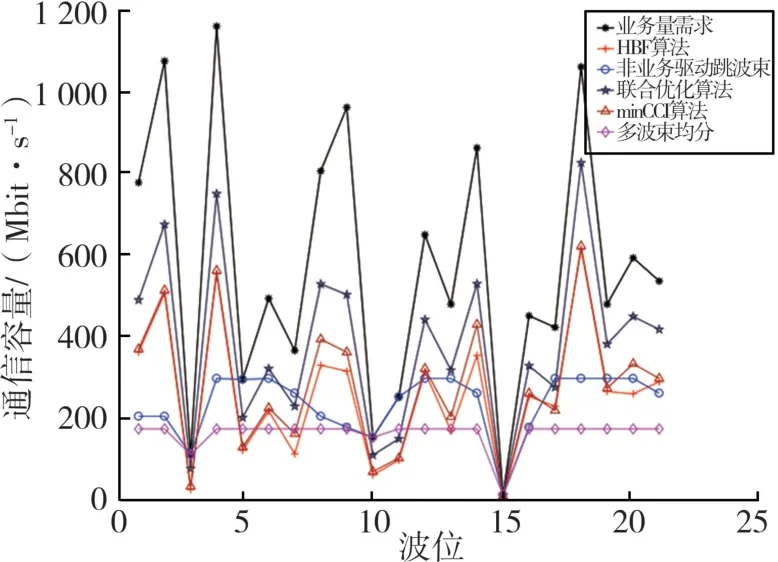
图6 系统吞吐量

从图中可以看出，本文提出的跳波束图案联合优化方法，要优于传统的跳波束图案设计方法。这是因为本文在通过凸优化算法求解时隙分配个数的基础上，不仅利用同频复用距离规避干扰，还针对前向链路波束间断的特点，综合波束重访时间、系统同步等因素，对时隙分配结果进行联合优化，避免了用户因失去同步而重新注册所带来的信息传输效率的降低。而在传统方法中，多波束均分和非业务驱动的跳波束算法因为缺乏资源分配的灵活性，所以系统性能较差；最小化同频干扰算法（minCCI）和最大波束优先算法（HBF）虽然都限制了同频干扰，而且HBF算法的时隙分配更为连续，但二者均未考虑波束间断带来的同步问题，所以在控制随业务波束的场景下，其系统吞吐量还有待提高。

最后，为了进一步探究业务量分布的不均性对算法性能的影响，在业务量分布的不同离散系数情况下，本文对系统的业务满意度进行了蒙特卡洛仿真。如图7所示，横坐标为业务量分布的离散系数，离散系数等于0，代表各波束业务量需求相同，此时业务量空间上均匀分布；离散系数越接近1，代表各波束业务量需求差异越大，空间分布越不均。

图7 各种算法的业务满意度

由图7可以看出，由于是资源受限系统，各波束的业务满意度均未达到100%，但本文提出的算法其业务满意度明显优于其他方法。随着业务需求分布变化，都能使得实际分配的容量更好地满足业务的动态变化和空间不均性分布。

4 结束语

针对跳波束系统中控制信令随业务波束的场景，本文提出一种联合优化的跳波束图案设计方法。在建立跳波束时隙分配目标函数的基础上，通过凸优化算法求解各波束分配的时隙个数，尽可能地满足各波束的业务需求；然后综合考虑同频干扰、波束重访时间、系统同步等因素，对时隙分配结果进行联合优化，确定各波束的驻留时间和工作次序。仿真结果表明，相比于传统方法，本文提出的跳波束图案设计方法，能够有效地消除系统内部同频干扰，解决波束间断带来的同步问题，大幅度提高系统吞吐量和业务满意度，使得实际分配的容量可以更好地满足业务的动态变化和不均性分布。