自聚焦圆贝塞尔高斯涡旋光束在自由空间中的传播特性
2021-08-25江骏杰邓冬梅
江骏杰,邓冬梅
(华南师范大学 广东省微纳光子功能与器件重点实验室,广东 广州 510631)
0 引言
2010年,Efremidis[1]等人首次提出了具有激增自聚焦特性的径向对称波包。这类光束有一个特殊的性质,即在传播过程中,它们的最大强度几乎保持不变,而在焦点处突然以数量级激增。与克尔介质(Kerr Media)产生的自聚焦效应不同的是,这类光束的自聚焦是纯线性的,是光场结构本身的结果[2]。随后,Efremidis[3]和Panagiotopoulos[5]通过实验证实这种光束确实存在。激增自聚焦光束在烧灼点的形成[3],介电微粒子的光学捕获和操纵[4,6,7]以及非线性强光子弹的产生[5]有着独特的应用前景。然而,对于传统的自聚焦光束而言,即环艾里高斯光束,对于较长的传播距离时,其自聚焦能力由于焦平面强度相对较低而受到限制。
1987年,Durnin等人推导出亥姆霍兹方程的精确解,即贝塞尔模式,是非衍射光束族的重要成员[8-10]。由于贝塞尔光束的准无衍射特性,它可以应用于不同的领域,如光学操控[11]、自由空间光通信[12,13]、显微镜成像[14]等。
光学涡旋(Optical Vortices)是一种具有螺旋相位波前,带有轨道角动量(OAM),能够携带不同拓扑电荷数的光束。对于有l个拓扑荷的涡旋光束,绕光束传播方向(z轴)一周,相位改变2lπ,光束横截面中心处振幅为0,在z轴上存在相位奇异。涡旋光束在光通信[15-17]、光学捕获[18]、光学显微镜[19]等方面有广泛的应用。近年来,嵌入不同类型自动聚焦光束的涡旋光束得到了广泛的研究[20-23]。
根据现有研究成果,提出一种可以在长距离内实现焦平面强度较高的自聚焦新型圆贝塞尔高斯涡旋光束(Circular Bessel Gaussian Vortex Beams,简称CBGVBs),并系统的研究了它在自由空间的传播特性。
1 同轴涡旋的自聚焦圆贝塞尔高斯涡旋光束的传播特性
我们假定CBGVBs在自由空间中传播,在傍轴光学系统中,波的复包络服从傍轴亥姆霍兹方程,即
(1)
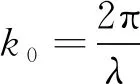
在柱坐标系中,带有同轴涡旋的CBGVBs初始光场表达式为
(2)
其中C为控制初始输入功率的无量纲常数,Jn为n阶第一类贝塞尔函数,当n=0时,r0为主环的半径,当n>0时,r0为两个主环的中点(如图1(a)所示),w0为长度参数,m为拓扑荷数,a为控制初始光束衰减的衰减系数,z为光束传播距离。
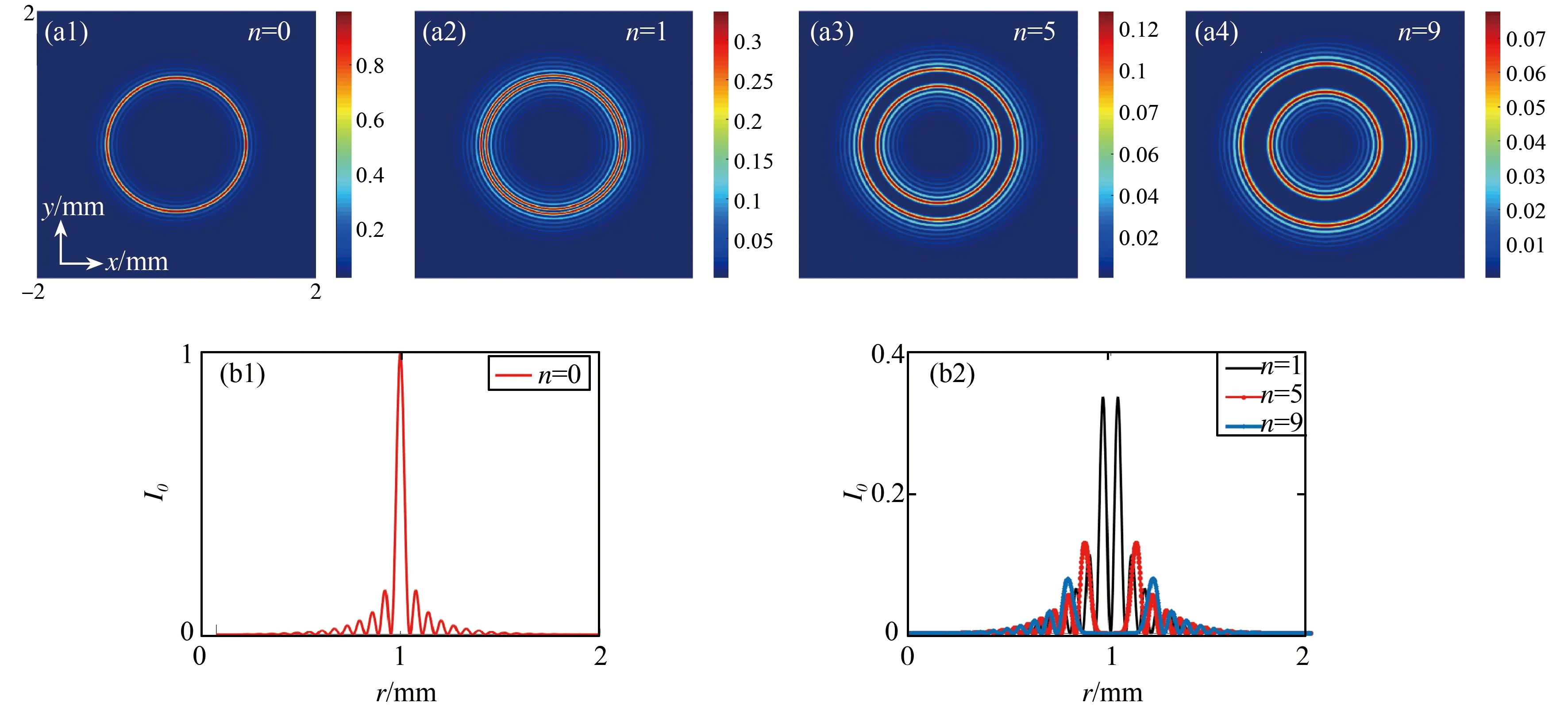
图1 (a) CBGVBs的横截面光场分布;(b) CBGVBs的初始强度I0与r的关系
由于CBGVBs在自由空间的传播解析表达式难以求出,我们这里将采用分步傅里叶循环的方法[24]来数值模拟其传播过程。若未作其他特殊说明,本文的部分参数选取如:C=1,r0=3 mm,w0=20 μm,a=0.001,n=1,λ=632.8 nm。
图1给出了部分CBGVBs的横向截面图以及光场分布情况,其中I0代表初始平面的光强,为了现象更加明显,这里我们取r0=1 mm,m=0。从图1我们可以看到,初始强度分布是关于r=r0对称的。从图1(a)我们可以看到,零阶CBGVBs在r=r0处有一个主环,而高阶的CBGVBs则有两个环且对称分布在r=r0的两侧。注意到在光束内部区域(r
图2展示了当m=0时,光束初始半径r0对聚焦特性的影响。图2(a)的纵坐标Imax/I0为归一化强度(任意位置的最大强度与初始输入强度的比值),而(c)中的FWHM为半高全宽(full width at half maximum)。从图2(a)我们可以看出随着r0的增加,归一化强度也随着光束功率的增加而增加。从图2(b)(c)中可以看出,CBGVBs的焦距和半高全宽几乎随r0的增加而线性增加。然而,如图2(d)所示,即使r0发生改变,焦平面内的光斑大小基本不变,半径约为53.7μm,因此,当我们缩放光斑的初始尺寸r0时,光束的聚焦特性即聚焦强度,焦距及半高全宽会同时发生改变。
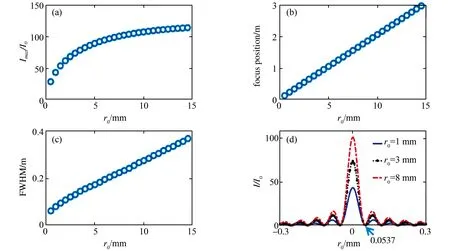
图2 聚焦特性与r0的关系 (a) Imax/I0与r0的关系;(b) 聚焦位置与r0的关系;(c) 半高全宽与r0的关系;(d) 不同r0对应的焦平面横向分布
图3给出了m=0和m=1的传播侧视图(z-y图)及部分截面图,其中colorbar代表归一化强度I/I0max(任意位置处的强度与初始输入强度最大值的比值),从图3的(a1)、(b1)可以看出CBGVBs沿z轴传播的过程中,强度不断增加,并在焦平面前激增自聚焦。同时,图3的(a4)、(b4)以及图2的(d)表明光束在达到焦平面前,光斑不断缩小,即强度不断向光束中心聚焦。与传统的圆贝塞尔光束相比(m=0),当m=1时,CBGVBs沿z轴存在一个由同轴涡旋引起的中空通道。从图4(b)我们可以看到,当m>0时,CBGVBs的归一化强度比m=0时要小得多。并且当m增大时,光束的归一化强度变小,而光束中心的零强度区域变大。这一特殊性在粒子捕获这一应用中有着极其重要的作用。近年来,圆贝塞尔光束已被广泛应用于粒子的操纵和捕获[10],与普通的光镊设置相比,因其突自聚焦特性而使用了放大率较低的物镜。但由于其在焦点处的强度分布不是中空的,传统的圆贝塞尔光束(m=0)不适合捕获折射率小于周围介质的微粒。并且传统贝塞尔光束并不携带轨道角动量,这在光扳手以及光镊的应用上是非常不利的。因此,焦平面为存在中空区域且携带轨道角动量的圆贝塞尔高斯涡旋光束有着更广泛的应用。此外,拓扑荷为m=0,1,2的CBGVBs分别在z=65.2,65.6,65.8 cm处聚焦。可以看到,当m上升时,聚焦位置也会稍稍后移。
图3 CBGVBs的传播侧视图及部分截面图 (a)m=0;(b)m=1 其中(a)(b)图的坐标上下对应
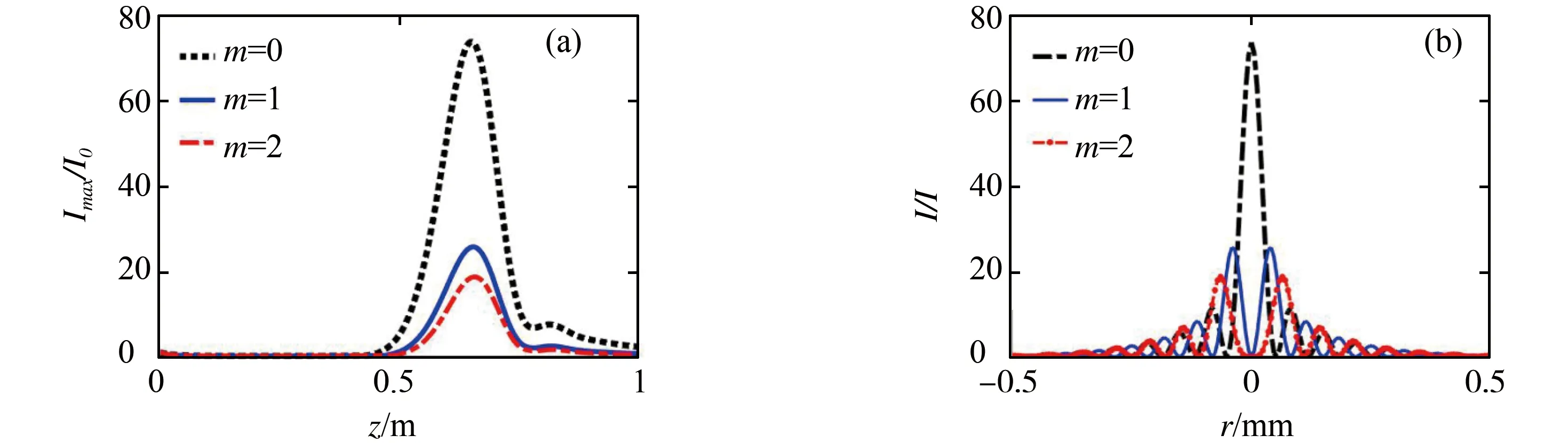
图4 (a) CBGVBs传播过程中的归一化强度与z和m的关系图;(b) CBGVBs在焦平面处的归一化强度与r和m的关系图
2 对称双离轴涡旋的圆贝塞尔高斯光束的传输特性
近几十年来,如何产生高质量的涡旋光场成为人们研究的一个热点内容,这其中就包括无衍射光束[25]。然而,在产生涡旋光束的过程中,较难保证涡旋轴与传播轴完全重合,也就是说产生的涡旋具有一定的离轴量。因此,研究离轴涡旋的圆贝塞尔高斯光束是十分有必要的,为了计算简便,我们假定两个涡旋沿x轴对称放置,则其光场表达式可写为
(3)
其中±代表涡旋方向,即拓扑荷为(+1,-1)或(+1,+1),两个涡旋的初始距离为2rk。
从图5(a1)-(b4)中,我们可以发现拓扑荷为(+1,+1)的两个光学涡旋叠加时,二者都有向中心收拢的趋势,并在焦平面处重叠但不完全重合(从相位图可以看出),同时,在光束的中心附近有两个中空洞,归一化强度较低。从相位图上可以看出,在光源附近存在两个相邻的奇点,即在传播过程中有两个相同的涡旋向光束中心偏移。然而,如果两个相反的涡旋加在CBGVBs上,它们在传播过程中发生碰撞并湮灭。归一化强度分布图(图5(b4))和相位图与m=0时CBGVBs的情况相似,只是焦平面的主瓣略微向上移动。
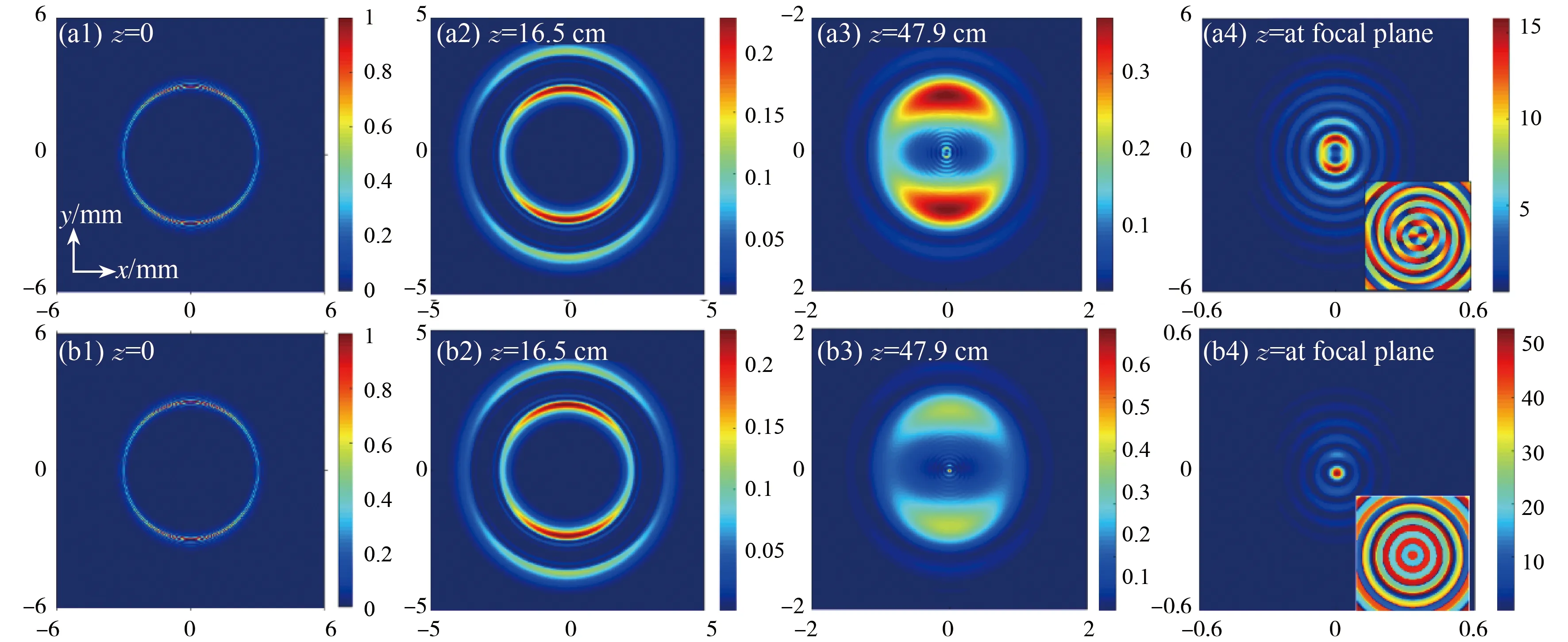
图5 CBGVBs部分传播侧视图,其中(a4)(b4)分别为焦平面(z=65.8,65.9 cm)的归一化强度和相位图,其中(a1)-(a4)的拓扑荷为(+1,+1),rk=1.5 mm,(b1)-(b4)的拓扑荷为(+1,-1),rk=1.5 mm
接下来,我们将研究不同涡旋位置而产生的影响。我们分别将涡旋放置在初始光束中空区域(rk=r0)以及区域外部(rk>r0)。如图6所示,当rk=r0时,其传播情况与rk=1.5 mm类似,但其沿x轴存在一条缝隙。焦平面内沿y轴存在两个主瓣,从其相位图我们可以看出,两个主瓣之间的相位差近似为π,相位沿x轴分布混乱。如图6(b1)-(b4)所示,当两个相反的涡旋位于入射光束的两个主环外时,焦平面的主瓣向下位移,与图5(b1)-(b4)中的情况相反。
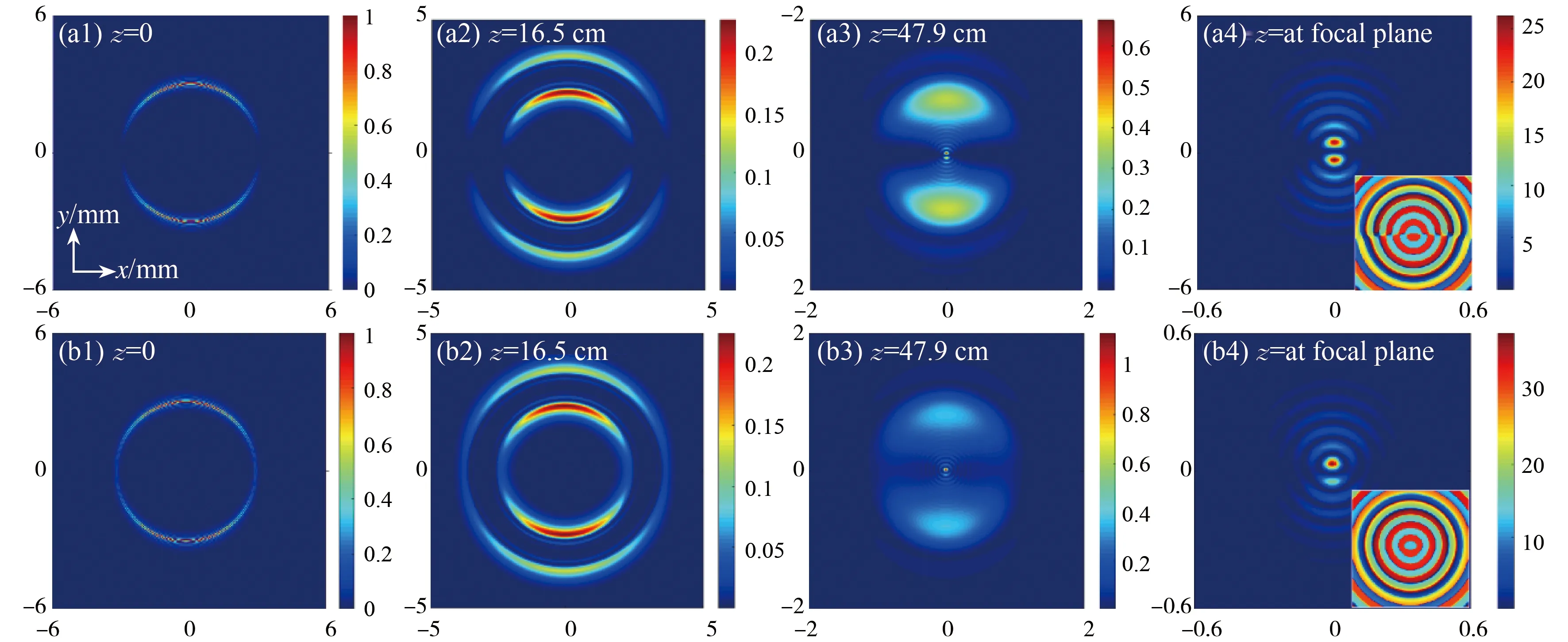
图6 CBGVBs部分传播侧视图,其中(a4)(b4)分别为焦平面(z=65.7 cm,z=65.2 cm)的归一化强度和相位图,其中(a1)-(b4)的拓扑荷均为(+1,-1),(a1)-(a4)中rk=3 mm,(b1)-(b4)中rk=4.5 mm
4 结论
本文系统地研究了CBGVBs在自由空间的传播特性,我们发现可以通过改变输入光束的尺寸r0来控制聚焦位置、聚焦强度和半高全宽。与传统的自聚焦光束相比,CBGVBs可以在更长的距离和更小的衍射范围内自动对焦。同时,得益于光学涡旋的作用,我们发现CBGVBs在焦平面处有一个中空区域,这一特性在捕获折射率小于周围介质的微粒有着重要的应用前景。除此之外,我们还讨论了带有双对称离轴涡旋的CBGVBs的性质,通过改变rk以及涡旋形式,涡旋会发生重叠,碰撞湮灭等等现象。
