高阶贝塞尔光束的Z扫描理论

陶华，刘永欣，蒲继雄

（华侨大学 信息科学与工程学院，福建 厦门 361021）

高阶贝塞尔光束的Z扫描理论

陶华，刘永欣，蒲继雄

（华侨大学 信息科学与工程学院，福建 厦门 361021）

以菲涅耳－基尔霍夫衍射理论为基础，研究高阶贝塞尔光束穿过非线性光学介质的衍射效应，从而解释高阶贝塞尔光束的Z扫描现象.通过对使用高斯光束、零阶贝塞尔光束、一阶贝塞尔光束、二阶贝塞尔光束和三阶贝塞尔光束的归一化Z扫描曲线对比，表明使用高阶贝塞尔光束较使用零阶贝塞尔光束的Z扫描具有更高的灵敏度.高阶贝塞尔光束的Z扫描为测量介质非线性光学系数提供了一种更为精确的测量方法.

高阶贝塞尔光束；Z扫描；非线性光学；归一化透过率；高灵敏度

Z扫描技术广泛应用于测量各种材料的光学非线性系数，这种方法最早是由Sheik－Bahae等人提出来的［1，2］.利用光通过薄的光学介质的自聚焦和自散焦作用，使介质在光传播的Z轴方向焦点附近移动，在远场小孔处观测光的强度变化.使用高斯光束、椭圆高斯光束、高斯－谢尔模型光束、拉盖尔－高斯光束、平顶光束、高斯－零阶贝塞尔光束的Z扫描方法已经得到了研究［1-8］.高阶贝塞尔光束作为波动方程的解，具有“无衍射”的特性，并且中心光强为零，利用拉盖尔－高斯光束照射轴棱锥可以得到高斯－高阶贝塞尔光束［9-12］，但是具有这种特征光束的Z扫描理论还没有得到研究，因此研究高斯－高阶贝塞尔光束的Z扫描是十分有必要的.

1 理论分析

如图1所示，高斯调制的高阶贝塞尔光束作为Z扫描实验过程的入射光束，在入射平面z＝0处的电场强度表达式为

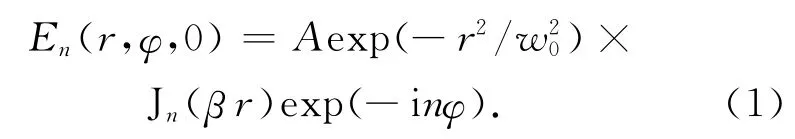
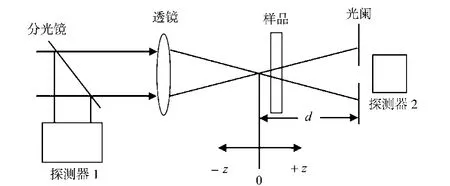
图1 Z扫描装置Fig.1 Schematic of Z－scan setup

式（1）中：Jn（r）为n阶一类贝塞尔函数；A 为振幅因子；w0为高斯分布的光斑尺寸大小；β为一个不变的常数.

高阶贝塞尔光束沿着Z方向传播，在非线性薄介质的入射平面的电场强度［13］可以表示为

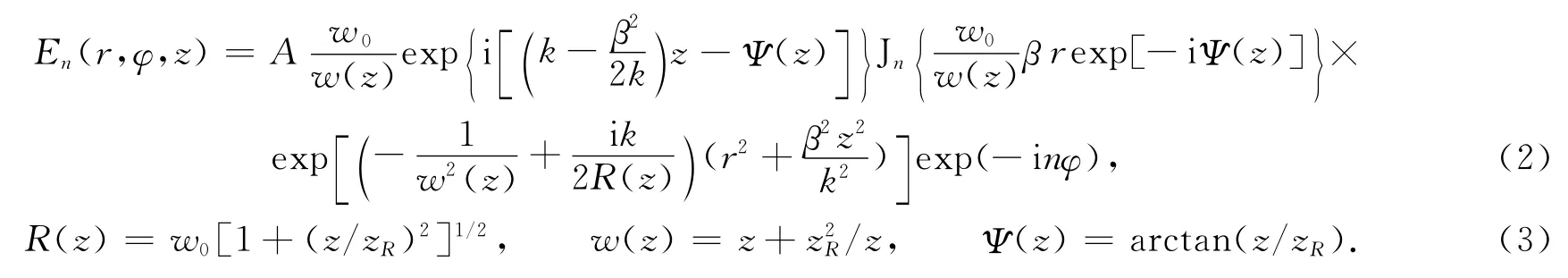
式（2），（3）中：R（z），w（z），Ψ（z）分别为高斯 －高阶贝塞尔光束的等相面曲率半径、束宽和相位因子；zR为瑞利半径，zR＝／2；k＝2π／λ为光波数，λ为入射激光波长.

高阶贝塞尔光束通过薄的样品介质，当介质的厚度足够薄时，以至于其中由于衍射和非线性折射引起的光束半径变化可以忽略不计［14］.当介质不存在非线性吸收时，可以得出在样品出表面的电场强度表达式为

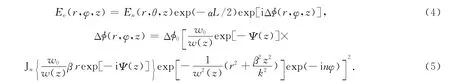
式（4），（5）中：α为线性吸收系数；L 为样品介质厚度；Δφ0为轴上焦点处的相移，Δφ0＝γkI0Leff，γ为非线性折射系数，Leff＝（1－exp（－αL））／α.

将式（4）中的非线性相移进行泰勒级数展开，可得

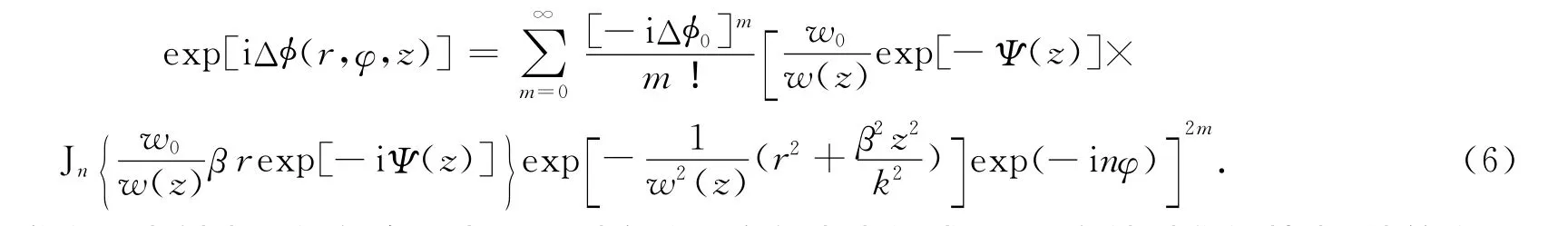
非线性光学介质出射表面的复合场由一系列高阶贝塞尔光束组成，且具有轴对称的特点.计算介质出射表面上每一点对轴上远场的贡献，远场接收屏上任意一点的衍射场分布由菲涅耳－基尔霍夫衍射积分公式［15］表达为

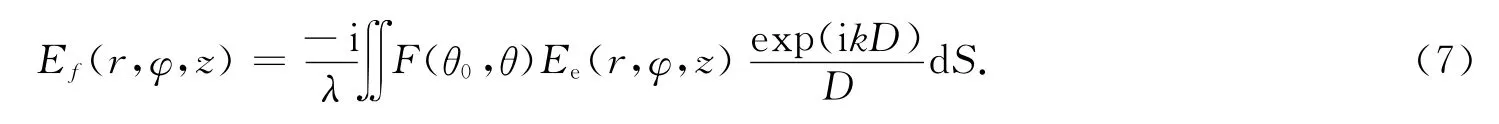
式（7）中：F（θ0，θ）为倾斜因子；D为衍射屏上点到接收屏上点的距离.

由于衍射屏是圆对称分布的，因而衍射场也是圆对称分布，对衍射屏和接收屏都采用极坐标.设z2为接收屏到衍射屏的距离，则D可表示为

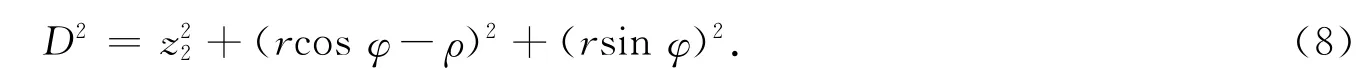
倾斜因子F（θ0，θ）＝（cosθ0＋cosθ）／2.其中：θ0为入射光与次波源的方位角，对于垂直入射，θ0＝0；θ为接收屏上场点相对于次波源的方位角，cosθ＝z2／D.

将式（4）～（6），式（8）代入式（7），可得到距离样品为z2的接收屏上的场分布为

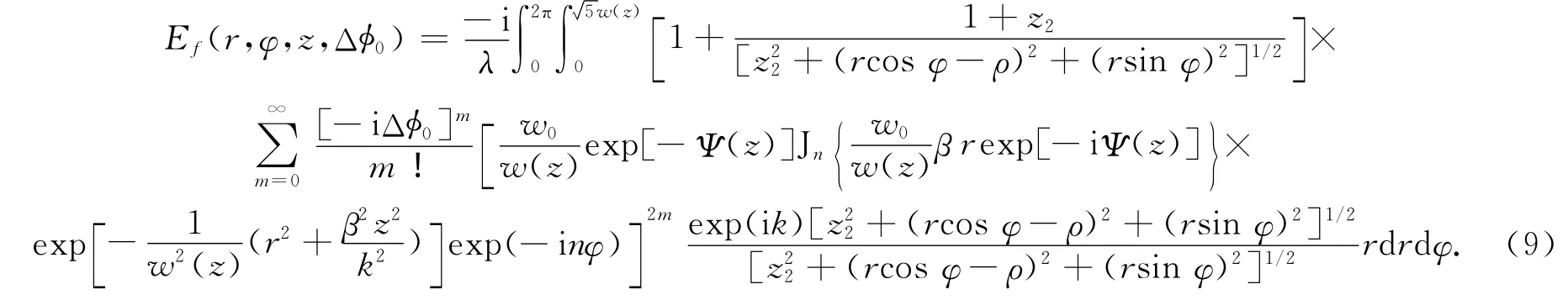
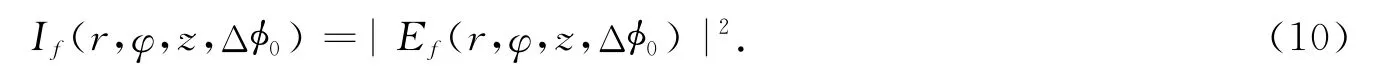
根据文献［2］，轴上点的Z扫描归一化透过率可以表示为

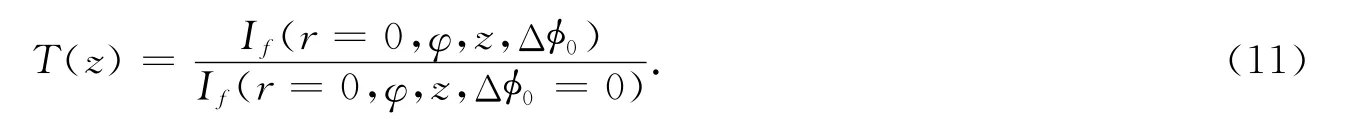
对于式（11）中的收敛无穷级数求和，当（Δφ0）N＋1／（N＋1）！＜0.03时，可以忽略N 阶项以后的项.因此，可以通过轴上焦点处的相移Δφ0值的大小，选择一个合适的阶数N来简化计算.

2 数值模拟

利用Mathcad软件，模拟一阶贝塞尔光束，得到在接收屏上的归一化一阶贝塞尔光束Z扫描曲线图，如图2所示.图2中的计算参数：n＝1，λ＝1.06μm，w0＝0.1mm，β＝3×104，α＝2×10－4m－1，L＝0.5mm，z2＝500mm，N＝10，Δφ0＝π.

从图2可知，高阶贝塞尔光束的Z扫描曲线先峰值后谷值，对应于负的非线性折射率介质；对于给定的Δφ0，只要小孔屏在远场条件（z2≫z）得到满足，T（z）的大小和形状与所用光束波长无关.在无非线性吸收的情况下，只要测得介质样品的Z扫描曲线，就可以得到介质样品的三阶非线性折射系数，它的符号可以由Z扫描曲线峰和谷的先后位置判断.此外，图2中的Z扫描曲线峰谷对称性和β的取值大小有关，这已经由Hughes等人的研究得到证明［8］.

利用Mathcad软件，分别模拟了高斯光束、零阶贝塞尔光束（n＝0）、一阶贝塞尔光束（n＝1）、二阶贝塞尔光束（n＝2）和三阶贝塞尔光束（n＝3）.为了对比以上5种光束对Z扫描灵敏度的影响，需要使得5种光束在非线性薄介质入射平面的光强最大值相等.5种光束在非线性薄介质入射平面的光强及在接收屏上的Z扫描曲线，分别如图3，4所示.图4中的计算参数：l＝1.06μm；w0＝0.1mm；β＝3×104；a＝2×10－4m－1；L＝0.5mm；z2＝500mm；N＝10；Δφ0＝π.图4的高斯光束的Z扫描计算方法由文献［1］中式（1）～（6）给出.

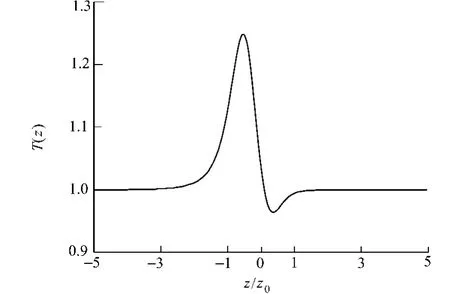
图2 归一化的一阶贝塞尔光束Z扫描曲线Fig.2 Normalized Z－scan transmittance of first－order Bessel beam

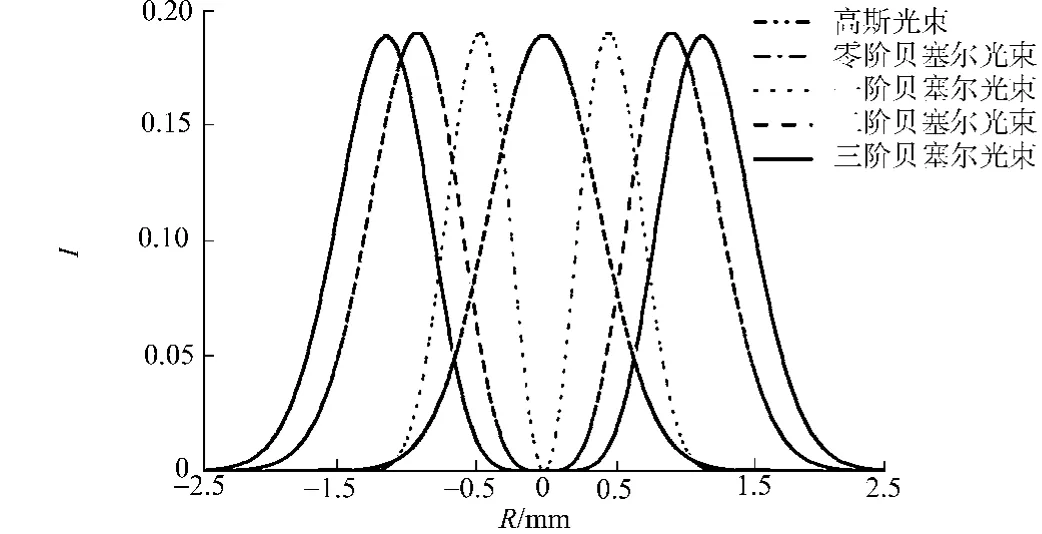
图3 光束在非线性薄介质入射平面的归一化光强Fig.3 Normalized intensity distribution of beam at incident plane of nonlinear thin optical media

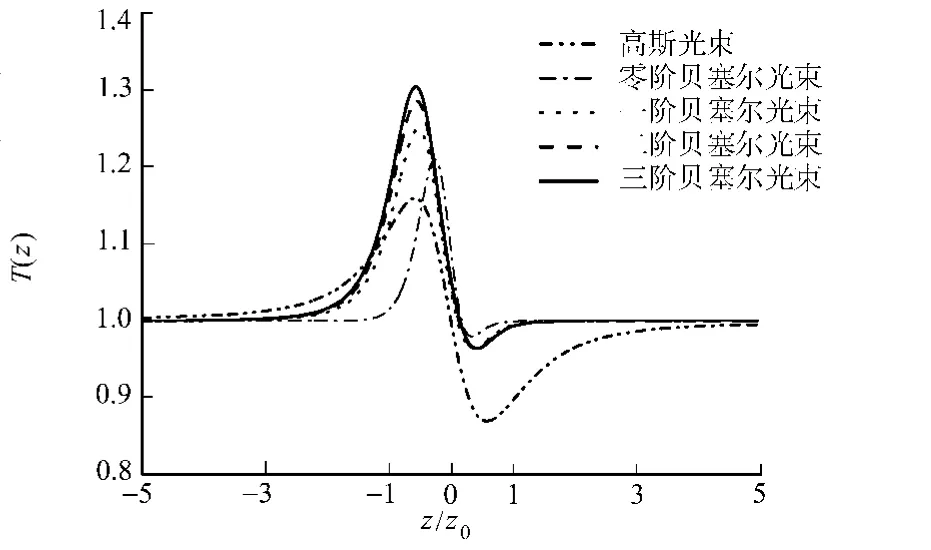
图4 光束的归一化Z扫描曲线 Fig.4 Normalized Z－scan transmittances of beam

由图3，4可知，零阶贝塞尔光束的归一化Z扫描曲线对比于高斯光束的归一化Z扫描曲线有一个高的峰值，这已经在Hughes等人的研究中得到证明［8］.由图3，4还可知，高阶贝塞尔光束的Z扫描曲线对比于零阶贝塞尔光束的归一化Z扫描曲线有一个更高的峰值.这由于高阶贝塞尔光束Z扫描探测器中心位于高阶贝塞尔光束光强最弱点，而零阶贝塞尔光束Z扫描探测器中心位于零阶贝塞尔光束光强最强点，从而导致任何相位或者强度变化破坏当前高阶贝塞尔光束分布的对称性都会造成一个大的正常值偏离［6］.

3 结束语

推导了高阶贝塞尔光束穿过非线性薄介质的Z扫描透过率，对比分析了高斯光束、零阶贝塞尔光束、一阶贝塞尔光束、二阶贝塞尔光束和三阶贝塞尔光束的Z扫描曲线.结果表明，使用高阶贝塞尔光束较高斯光束和零阶贝塞尔光束的Z扫描有更高的灵敏度.高阶贝塞尔光束的Z扫描为测量材料非线性光学系数提供了一种更为精确的测量方法.

［1］SHEIK－BAHAE M，SAID A A，VAN－STRYLAND E W.High－sensitivity，single－beamn2measurements［J］.Opt Lett，1989，14（17）：955－957.

［2］SHEIK－BAHAE M，SAID A A，WEI T，et al.Sensitive measurement of optical nonlinearities using single beam［J］.IEEE J Quantum Electron，1990，26（4）：760－769.

［3］MIAN S M，TAHERI B，WICKSTED J P.Effects of beam ellipticity on Z－scan measurements［J］.J Opt Soc Am B，1996，13（5）：856－863.

［4］TSIGARIDAS G，FAKIS M，POLYZOS I，et al.Z－scan technique for elliptic Gaussian beams［J］.Appl Phys B，2003，77（1）：71－75.

［5］LIU Y，PU J，QI H.Investigation on Z－scan experiment by use of partially coherent beams［J］.Opt Commun，2008，281（2）：326－330.

［6］ZHANG W，KUZYK M G.Effect of a thin optical Kerr medium on a Laguerre－Gaussian beam［J］.Appl Phys Lett，2006，89（10）：101－103.

［7］ZHAO W，PALFFY－MUHORAY P.Z－scan measurement of x（3）using top－hat beams［J］.Appl Phys Lett，1993，65（6）：673－675.

［8］HUGHES S，BURZLER J M.Theory of Z－scan measurements using Gaussian－Bessel beams［J］.Phys Rev A，1997，56（2）：R1103－R1106.

［9］DURNIN J，MICELI JR J J，EBERLY J H.Diffraction－free beams［J］.Phys Rev Lett，1987，58（15）：1499－1501.

［10］ARLT J，DHOLAKIA K.Generation of high－order Bessel beams by use of an axicon［J］.Opt Commun，2000，177（1／2／3／4／5／6）：297－301.

［11］PORRAS M A.Diffraction－free and dispersion－free pulsed beam propagation in dispersive media［J］.Opt Lett，2001，26（17）：1364－1366.

［12］LÓPEZ－MARISCAL C，GUTIÉRREZ－VEGA J C，CHÁVEZ－CERDA S.Production of high－order bessel beams with a Mach－Zehnder interferometer［J］.Appl Opt，2004，43（26）：5060－5063.

［13］PALMA C，BORGHI R，CINCOTTI G.Beams originated by J0－correlated Schell－model planar sources［J］.Opt Commun，1996，125（1／2／3）：113－121.

［14］WEAIRE D，WHERRETT B S，MILLER D A B，et al.Effect of low－power nonlinear refraction on laser－beam propagation in InSb［J］.Opt Lett，1979，4（10）：331－333.

［15］姚保利，任立勇，侯洵 .基于衍射模型的Z扫描理论［J］.光学学报，2002，22（1）：19－23.

Z－Scan Measurement Theory of the High－Order Bessel Beam

TAO Hua，LIU Yong－xin，PU Ji－xiong
（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

Based on the Fresnel－Kirchhoff diffraction theory，the diffraction effects of high－order Bessel beams through the nonlinear optical media are analyzed，which can explain the Z－scan phenomena of high－order Bessel beams.By comparing the normalized Z－scan transmittances of Gaussian beam，zero－order Bessel beam，first－order Bessel beam，secondorder Bessel beam and third－order Bessel beam，it is shown that Z－scan using the high－order Bessel beam has a higher sensitivity than that using the zero－order Bessel beam.The Z－scan with the high－order Bessel beams may provide a precise method for measuring the nonlinear coefficients of optical media.

high－order Bessel beams；Z－scan；nonlinear optics；normalized transmittance；high sensitivity

钱筠 英文审校：吴逢铁）

O 436

A

1000－5013（2012）01－0009－04

2011－03－11

蒲继雄（1962－），男，教授，主要从事光束传输与非线性光学的研究.E－mail：jixiong＠hqu.edu.cn.

国家自然科学基金资助项目（60977068）；中国科学院瞬态光学与光子技术国家重点实验室科研基金资助项目（SKL－ST200912）；国务院侨办科研基金资助项目（10QZR03）