二维弹道修正弹及其制导控制技术综述

邢炳楠，杜忠华，杜成鑫

(南京理工大学 机械工程学院 智能弹药技术国防重点学科实验室， 江苏 南京 210094)

随着科学技术的发展，制导弹药的种类和作战效能也随之发生着巨大变化。迄今为止，制导弹药包括制导航弹、制导炮弹、弹道修正弹、制导火箭弹等。弹道修正弹的基本概念是将传统榴弹、迫击炮弹或火箭弹的引信换装成弹道修正模块，根据卫星制导模块或地面(舰载)雷达探测到的信息，判断实际弹道与理想弹道的偏差进行修正[1]。可以在全弹道上进行有限次修正，也可以只在弹道末段或弹道起始段进行修正。区别于导弹对弹道的无级修正进而直指目标，弹道修正弹通过有限次的修正来减小散布，提高毁伤概率。而导弹要求百发百中，修正弹只期望落在以目标为中心的小区域内。正是以上差别决定了导弹和修正弹属于不同打击精度弹药，成本差异显著。

由于通常需要改换普通弹丸的引信模块，修正弹的设计往往面对特殊的工程约束。同时，较高的发射过载，往往意味着修正机构的执行能力被牺牲在鲁棒性和发射寿命上。而面对高维非线性、多约束条件、时变性的动力学系统，修正控制系统设计也更为困难。因此，对微型化且响应迅速的修正引信模块的设计，以及高精度、高可靠性的制导控制方法的研究提出了更大的挑战，引起了学者们的广泛关注，多位学者对修正弹的研究工作进行了综述。张民权、张冬旭及彭博等[2-4]主要针对一维及二维弹道修正弹，对其不同类型的修正执行机构的工作原理及特点进行简单分类概述。高敏和梁志剑等[5-6]从弹道修正弹的主要探测技术方面进行介绍总结。李鑫鹏等[7]则着重对弹道修正引信旋转隔离技术的作用、工作环境和工作要求展开综述。柯知非和雷晓云等[8-9]在介绍不同二维修正弹机构方案的基础上，进一步对主要控制算法研究概况进行了阐述。上述文献针对不同类型的修正执行机构，分别在修正机理和技术特点、弹道探测技术等方面进行了充分的综述。但对于整个修正过程而言，包括气动参数辨识及状态估计、修正机构参数优化设计及制导律等在内的控制方法亦是弹道修正的核心内容，并直接影响最终的打击精度。本文将从二维弹道修正弹的执行机构发展分类、任务分析和修正控制算法方面进行综述，旨在：①跟踪二维弹道修正弹的发展前沿，梳理发展脉络，揭示其发展规律；②分析修正弹在不同弹道测量技术方案下制导与控制系统的总体任务；③着重从包括神经网络、群智能算法在内的智能控制算法角度，对弹道修正弹制导及控制方法的研究现状进行综述，并总结发展趋势以提出展望。期望在对二维弹道修正弹有全面了解的基础上，聚焦智能化的制导控制技术，为精确打击弹药的发展提供有益的参考。

1 二维弹道修正弹国内外研究现状

1.1 二维弹道修正弹的发展

国外对于修正弹的研究起步较早，经过不断的发展，美国、瑞典、法国、英国、德国、俄罗斯、意大利、以色列等国均取得了一定成果，并相继实施了多项计划。技术基础决定了修正弹的发展走向。随着卫星导航系统(如GPS、北斗等)、惯性导航系统(Inertial Navigation System，INS)、专用集成电路(Application Specific Integrated Circuit，ASIC)、微机电系统(Micro-Electro-Mechanical Systems，MEMS)和灵巧结构技术的发展，经历了大约50年，弹道修正弹也得以从一维修正发展至二维修正。目前，国外一维修正弹的技术已经比较成熟，现阶段工作均致力于二维修正弹研究。

图1 BAE系统公司开发的CCFFig.1 CCF developed by BAE Systems

作为世界第一大军事强国，美国在修正弹的研究上一直处于领先状态。20世纪70年代中期，美国最早提出了弹道修正弹的概念，当时被称作末端修正的旋转稳定弹(Terminal Corrected Spinning Projectile, TCSP)[10]。20世纪80年代末，美国又提出了低成本有能力弹药(Low Cost Competent Munitions，LCCM)计划，该计划共包括GPS射程修正、一维增阻弹道修正和二维弹道修正三个阶段。在前期一维修正研究基础上，美国先后研发了弹道修正引信(Course Correcting Fuze， CCF)、制导一体化引信(Guidance Integrated Fuze， GIF)和精确制导组件(Precision Guidance Kit，PGK)三个典型代表系列产品。二维弹道修正引信由北美BAE系统公司推出，其设计概念源于TCSP，且该产品于2005年6月实弹试验成功，这也是二维弹道修正引信的首次亮相。同一时期，美国开始了一项GIF项目，但该项目由于后期研究困难而终止。CCF和GIF均以M782多功能炮兵引信为基础对传统引信进行改造，其修正引信结构分别如图1和图2所示。由图1和图2可知，CCF和GIF的设计结构存在明显差异。CCF主要采用纵向增阻，横向减旋的方式实现修正；GIF则加装减旋轴承，改变传统弹道修正组件与弹体连接方式，通过栅格状鸭舵偏转完成修正。同时，GIF采用GPS/INS组合探测的方式，但CCF仅依靠GPS提供导航定位信息。但殊途同归，CCF和GIF技术的发展都为多年后的PGK项目提供了研究基础。PGK结构如图3所示，是一个分阶段螺旋式发展的研究计划，其间推出了美国目前最为成熟的二维修正引信产品。尽管其打击精度略低于早期的“神剑”远程制导炮弹，但成本却降低了85%，这也决定了美国后期对PGK的加速研究和生产。该产品在实战中的良好反响，意味着美国在二维修正技术和固件小型化方面取得了关键性进展。同时，在PGK项目基础上，迫击炮弹制导组件(Mortar Guidance Kit，MGK)项目的成功实施进一步表明PGK具有可移植性好、研制周期短、能有效提高射击精度的优点。

图2 美国GIFFig.2 GIF in USA

(a) PGK正视图(a) Front view of PGK (b) PGK立体示意图(b) Stereogram of PGK图3 美国PGKFig.3 PGK in USA

表1给出了国外(美国除外)在二维弹道修正领域的积极探索成果。早在20世纪90年代起，意大利致力于发展海军精确打击力量，先后研制了76 mm和127 mm的舰载反导弹弹道修正弹和“火山”这两款代表修正弹，并在后期继续拓展其应用平台。以色列和俄罗斯两个传统军事强国则更青睐于大口径的二维弹道修正弹的研制，例如均有可实现火力压制的300 mm弹道修正火箭弹的成熟产品。此外，以PGK代表的气动鸭舵式二维修正结构提供了良好的研究模板，以色列的155 mm“Top Gun”和“银弹”均是该类型产品，再次验证了该类型修正组件的优越性能。同时，从法国、瑞典、德国弹道探测方式上可以看出，修正弹的发展与GPS、惯性导航和其他姿态测量技术的发展密切相关，这些技术的成熟使得从早期的半主动雷达探测方式到后期多模组合探测方式的转变成为可能。此外，MEMS和电器元件加固等技术的进步，有助于实现修正组件结构趋于紧凑模块化设计并解决高过载的问题。以色列IMI公司独立开发应用于CTAP修正弹上的“Pure Heart”制导模块就是该类技术的典型体现。

综上所述，各国在二维修正弹领域进行着持久不懈的探索与研究，不断推进精确打击技术的发展。纵观其发展历程，总结特点如下:

1)重视鸭舵类修正机构。各国对二维修正技术处于积极探索阶段，尽管各国修正机构类型不尽相同，但有赖于鸭舵式导弹设计和鸭舵类型修正机构的实战成功经验，该类型二维修正弹是当下研究的热点。

2) “螺旋”式发展模式。在修正组件研制后期，各国均致力于拓展其不同口径、不同原理和不同作战平台下的进一步应用，以提高系列化产品性能。

3)探测技术多模复合化。为弥补单一探测方式误差，提高探测系统的抗干扰性，各个国家在弹道数据探测方面多采用多模组合的方式。

4)高效集成化设计。受限于设计空间，同时为提高修正组件的模块化和通用化设计性能，各国修正组件设计趋向于微型化，这也促进了对发展微机电技术的重视。

我国于20世纪90年代末开始弹道修正弹的研究工作，但目前水平仍处于LCCM的第二阶段。对于二维弹道修正弹这种可提高常规无控弹药精确打击的理想模式研究，仍处于技术预研和储备阶段。但最近几年我国推出的以WS-22、WS-35地面火力系统产品配套系列弹药已经属于弹道修正弹范围。考虑到信息化武器装备的战略需求，弹道修正弹作为低成本的精确打击弹药的典型代表，具有非常大的发展空间。重视对传统库存弹药的智能化改造，加快二维修正弹中探测导航、微机电系统等关键技术的探索与突破，满足低成本、高射击精度的军事需求，对提高我国炮兵武器在未来战争中的适应性和作战效能具有重要意义。

1.2 二维弹道修正弹任务分析

二维弹道修正弹的实质是通过修正机构产生控制力对飞行弹道的纵向射程误差和横向方向误差进行修正，从而提高弹丸的落点精度和毁伤效率，其修正过程如图4所示。二维弹道修正弹系统分解情况如图5所示，根据二维修正弹工作原理，可将整个系统分解为目标探测系统、弹道偏差解算系统和弹道控制系统三个主要子系统，其中弹道偏差解算系统由弹丸姿态探测系统和解算装置共同组成。在弹丸飞行过程中，根据目标运动参数(目标探测系统所得)和飞行弹道参数(弹丸姿态探测系统所得)进行解算获得弹目偏差信息，进而结合弹丸的姿态参数弹道控制系统可实现对修正机构的控制，最终完成修正弹道的任务。由以上过程可知，修正机构技术、外弹道参数辨识技术和制导控制算法均是影响二维弹道修正系统实现的关键技术。

表1 国外弹道修正弹发展时间表

图4 二维弹道修正弹修正过程示意图Fig.4 Process diagram of two-dimensional trajectory correction projectile

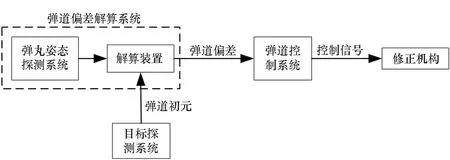
图5 二维弹道修正弹系统分解图Fig.5 Decomposition map of two-dimensional trajectory correction projectile system

2 二维弹道修正弹修正机构研究现状

就目前已有及在研的二维弹道修正弹，根据产生控制力的方式可将修正方式分为如下三种：一种是气动力控制方式，通过空气动力来产生法向力，包括鸭舵式、微扰流片式和增阻式等修正机构；另一种是直接力控制方式，如脉冲矢量发动机和射流式修正机构等；还有一种则是以变质心类修正机构为代表的惯性力控制方式。

2.1 基于气动力控制修正机构

鸭舵式修正机构是目前气动力控制修正机构的主要研究对象。通过鸭舵修正机构改造常规非制导弹药实现智能化并不是一个新的概念，其设计理念借鉴自导弹。早期研究中，Costello对鸭舵布局的尾翼稳定弹弹道特性进行了分析，研究结果表明：该类型修正机构可使弹丸射程显著增加，但弹丸的末速度明显降低，飞行时间大大增加[11-12]。目前，固定偏角式“十”字鸭舵修正机构得到了国内外学者的广泛关注，美国PGK和以色列“银弹”等均是该类修正结构的典型代表。该修正结构包括一组用于减旋的旋转鸭舵(减少弹体旋转对修正机构的影响)和一组用于提供转向力矩的控制鸭舵(实现二维修正)。

目前，针对固定式鸭舵修正机构，有以下两方面研究受到学者们的关注。一方面是减旋目的设计的隔转式鸭舵修正机构。其设计概念最早由Regan等提出，并从弹道飞行稳定性角度论证了方案的可行性[10]。随后，Costello等对隔转式鸭舵修正机构的研究作出了突出贡献，在此类特殊结构修正弹的动力学建模[13-14]、稳定性分析[15-16]、机动性能分析[16]和制导控制系统设计方面[17-19]做了大量研究。由于其独特的前体减旋设计，该类修正机构能够实现较为精确的弹道控制。因此，近些年来许多国内学者在动力学及气动特性分析、减旋机构设计等方面也展开了相关探索[20-23]。另一方面，由于成本低、执行机构简单、响应速度快的优点，如图6所示的伸缩式鸭舵修正机构成为一项研究热点。相比传统鸭舵修正机构，伸缩式鸭舵修正机构在不需要修正时，可将舵片缩回弹体内以减小空气阻力、增大弹丸射程。文献[24]讨论了这种新的修正设计所导致的气动布局非对称情况，研究证明该设计仍然具有抵抗外界干扰的能力，以保持飞行稳定性[25]。进一步地，唐玉发和谢克峰等针对伸缩式鸭舵修正弹的舵机优化设计[26]、修正策略[26-27]和执行机构工况[28]进行了研究，通过分析鸭舵在伸展收缩过程中的动力学特性，确定了舵机相关驱动部件的最佳工作区间，仿真计算结果表明：所设计方案均可满足工程需求。

(a) 舵片收缩(a) Retraction of canards

(b) 舵片伸展(b) Extension of canards图6 伸缩式鸭舵修正机构工作示意图Fig.6 Schematic diagram of reciprocating canards correction mechanism

除以上修正机构外，增阻式和微扰流片式修正机构也是气动力修正机构的代表。增阻式修正机构最初在美国专利中被提出[29]，主要由阻力环和阻尼片组合实现二维弹道修正。其中，阻力环实现射程偏差修正，阻尼片实现横向减旋修正。微扰流片是另一种气动力修正结构，通过弹箭外流场形成微小持续的扰动，改变弹箭的飞行状态实现修正，较好地提高弹箭气动控制效率[30]。除了传统意义上固态片状的扰流片，还有一类更为特殊的扰流片，如图7所示，其设计特点在于在弹箭尾部开设能够喷射出合成流体的槽口。文献[31]指出此类修正机构对超音速尾翼稳定弹具有良好的控制效果，控制能力与鸭舵装置相似，但其在不使用时扰流片可缩回弹体，以减小飞行阻力。同时，扰流片与弹体之间较小的距离可减小伸展时产生的阻力。

图7 微扰流片式修正弹示意图Fig.7 The diagram of two-dimensional trajectory correction projectile based on micro spoiler

2.2 基于直接力控制修正机构

脉冲修正机构(如图8所示)，在弹顶部或弹丸质心附近横截面内沿周向均匀布置数对微型脉冲火箭发动机，根据脉冲火箭发动机点火产生的喷射气流的反作用力，增大弹丸速度或改变弹丸运动方向，实现弹丸距离和方向的二维修正[32]。瑞典的4PGJC，意大利的CCS舰炮以及美国的ERGM-EX-171均是采用脉冲修正机构的二维修正弹的典型代表。脉冲力对弹道的修正本质是对速度的修正，显然，脉冲力作用下弹丸轴向和偏流方向速度的改变量是不同的，所以对弹丸纵向和横向的修正能力也不一样[33]。垂直方向速度的变化主要导致弹丸飞行时间的改变，进而影响落点位置；而横向速度的改变则直接导致落点变化。与传统带斜角的翼片或鸭舵式修正结构相比，脉冲作用的特点是响应速度快，而且推力大小稳定，不依赖于导弹的飞行环境[34]。

图8 脉冲式二维修正弹剖视图Fig.8 Section view of two-dimensional trajectory correction projectile with pulse jet control mechanism

国外早期研究主要集中于利用弹丸线性化理论分析脉冲作用对于弹丸弹道运动特性的影响，以期为后续的控制设计提供理论参考。Guidos等[35-36]对尖脉冲和方波脉冲两种不同形式下弹丸角运动特性的变化进行了研究，并给出其解析解表达式。Burchett[37]和Jitpraphai[38]针对同一类火箭弹的脉冲修正机构的较大落点散布问题进行了研究，侧重于分析主要影响因素并给出使得落点散布误差稳定减小的具体控制方法。Corriveau等[39]提出了一种在旋转稳定弹丸上采用双脉冲推力器的方法，以使横向修正最大化，同时使角运动引起的射程损失最小。同时，提出了该结构下的三个稳定准则，它们规定了弹丸上脉冲相对于重心的位置、脉冲相对于彼此的方向以及两个脉冲之间的时间。文中所建立的线性化攻角运动模型能较准确地预测弹丸的角运动和横向速度。以上研究均为脉冲修正机构参数设计提供了理论依据。

在国内研究方面，施坤林[40]分析了脉冲修正弹的动态响应特性及响应谱，指出攻角最大值不是发生在修正冲量消失的瞬间，而是要滞后一段时间才发生。在修正冲量消失后，弹丸将绕质心做有阻尼衰减的振动运动。同时，采用侧喷脉冲发动机进行末端修正的弹丸，发动机喷口位置在弹丸质心附近有一个“稳定区”。此外，姚文进、曹小兵等在其博士论文中对不同脉冲参数下的弹道诸元的变化规律进行了研究。曹小兵进一步给出了脉冲修正下的攻角与脉冲冲量及轴向偏心距之间的解析关系[32，41]。杨红伟等研究了制导炮弹受侧向脉冲推力作用后处于大攻角情况下的非线性运动稳定性问题。应用首次积分描述了弹丸的运动方程，给出了弹丸非线性运动稳定的充分条件，为非线性运动条件下弹丸的飞行形态的预测、脉冲执行机构的设计等问题提供了一定的理论依据[42]。值得注意的是，脉冲修正机构不仅在改造常规炮弹领域有应用。文献[43]针对一种同时存在空气舵和脉冲推力器两种修正机构的复合拦截弹为对象，对气动力和直接力产生的姿态控制冗余问题，及侧喷流场和外界来流存在的喷流交感效应进行重点研究。事实上，喷流交感效应的复杂机理在修正弹领域也是值得深入研究的重点。

图9 典型的射流元件工作原理图Fig.9 Schematics diagram of typical fluidic thrust control mechanism

射流执行机构是目前在研的另一种直接力控制修正机构，该结构广泛应用于无人驾驶作战飞机，近些年作为一种修正执行机构引起学者们的关注[44]。典型的射流执行机构原理如图9所示，通过控制进气道的开闭，拉瓦尔喷管式的气流通道结构可对流过的空气进行加速，弹体侧面高速喷出形成的气体可产生一定的侧向修正力。而弹丸飞行速度、所处的气流场及气流通道的设计精度是影响修正力的主要因素。此外，根据试验可知，射流力的切换会造成10～30 ms的时间延迟，导致修正滞后，进而影响修正精度和实际应用的难度。因此，如何解决延时散布问题是目前射流执行机构研究的难点所在[45]。

2.3 基于惯性力修正机构

变质心类修正机构作为一种新式修正方式，其概念源自飞机自动驾驶仪的设计。它由执行机构移动飞行体内部的质量块，使飞行体质心位置在一定空间范围内移动，从而通过改变弹体所受的力矩来改变飞行体的飞行姿态，以达到对弹头机动控制的目的[46]。其基本工作原理如图10所示。

图10 变质心控制机构的基本原理Fig.10 Basic principle of moving mass control mechanism

默朝明[47]提出一种基于摄动原理研究滑块以单次移动的方式进行弹道修正的方法。对于给定的发射条件，研究了给定质量和移动范围的滑块对炮弹弹道的修正范围。同时，采用遗传算法研究了能够满足修正要求的前提下滑块的最小移动范围。Frost等[48]在基于变质心修正机构方面做了很多研究，建立了含轴对称旋转质量块的匀速旋转弹丸的运动方程。利用改进过的弹丸线性理论，系统研究了内部质量块的配置参数影响。进一步，根据所建立的七自由度飞行动力学模型，将其应用于装有内部不平衡旋转部件的尾翼稳定弹丸和自旋稳定弹丸的弹道预测[49]。并指出越早开始控制，所获得的控制能力就越大。但平均飞行速度对两种系统控制能力的影响则不同。Rogers等[50]的研究表明，弹丸的转向是由振荡质量和弹丸旋转之间的动态耦合引起的。执行机构力和功率的大小要求随滚速和内部质量的增加而增加，但对空腔偏移距离和弹丸静裕度的变化不敏感。但目前研究显示，变质心控制技术目前还只应用于再入飞行器、航天器等领域，尚未见有基于此类技术的成熟修正弹产品。

上述典型的修正机构在实现二维弹道修正上各具优缺点，适应场合亦不相同。鸭舵修正机构目前最为成熟且多于旋转稳定弹丸，能够提供连续控制力，修正精度较高。但该修正机构复杂，成本高，存在机械滞后阻尼，响应时间较长，不能进行滚转控制。作为将来弹道修正弹的主要发展方向，微型化是鸭舵修正机构研究最大的障碍[3]。微扰流片作为一种应用较少的弹道修正机构，与鸭舵相比，具有简单、体积小、成本相对较低的优点[30]。而增阻型二维修正技术只需要测量质点弹道，属于开环控制，技术实现相对简单，但目前由于控制效果并不理想，相关研究相对较少[51]。与气动力控制相比，脉冲力控制技术具有以下优点：响应时间短，反应速度快；环境适应性强，工作效率高；易于全弹结构优化以提高总体性能。然而，由于脉冲力控制不能实施连续修正，修正效果具有离散性。但鉴于其绝对优势远超过相对劣势，目前仍是被优先考虑的弹道修正技术。射流修正机构的主要缺点在于易受环境限制和修正滞后影响，增加了实际应用的难度。变质心技术其优势在于，由于修正机构置于弹体内，可以有效改善气动类修正机构在稀薄大气层内控制能力不足的缺点；使用该类修正机构无须改变弹体外形结构，从外形上可较好减少在高速飞行中烧灼等原因对该控制方法产生的影响。与直接力控制方法相比，无须考虑侧喷扰动和携带燃料的问题，因此具有较大的有效载荷，这一点比直接力控制方法更有优势[52]。

3 二维弹道修正弹算法研究

3.1 气动参数辨识及状态估计算法

无论何种弹道探测手段，所得原始数据均包含一定噪声。同时对于多模组合的探测方式，往往还需考虑信息融合的问题。对含噪声的原始数据合理处理，准确完成对未知弹道参数的确定，即为气动参数辨识及状态估计的主要工作。针对非线性模型中有效处理含噪声的参数辨识及状态估计问题，目前研究应用较多的当属各种形式的卡尔曼滤波算法。卡尔曼滤波算法能将参数估计问题转化为状态估计问题，依据飞行器系统的实际情况，采用连续估计模型，并通过离散时间测量与离散滤波算法达到实时估计[53]。扩展卡尔曼滤波(Extended Kalman Filter, EKF)、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)则是其中的典型代表。早期研究中，Speyer比较了几种用于寻的导弹制导的滤波方法，发现标准EKF相对于迭代EKF、修正高斯二阶滤波器和自适应EKF而言，总体性能最佳[54]。文献[55-57]则对UKF及混合卡尔曼滤波算法在处理组合融合数据方面进行了研究，研究结果表明，所提算法可实现较高精度的参数估计。

目前，国内外学者的研究集中于提高数据处理的准确度和实时性以及提高机动目标打击能力两个方面。一方面，为提高传统卡尔曼滤波算法状态估计性能，一些相关变体及新的理论得到了学者们的注意。龙正江[58]基于扩展质点弹道模型的状态方程和GPS测量数据的线性测量方程，证明了衰减记忆混杂卡尔曼滤波算法能在一定精度条件下极大地减小在线计算量，提高参数辨识过程的实时性。而采用最小偏度单形采样能够减小无迹卡尔曼滤波算法的计算量，提高计算实时性。普承恩等[59]提出一种将拓展卡尔曼滤波与敏感矩阵结合的落点预测制导方法，并验证了该算法可满足弹载计算机快速性和实时性的要求。然而，基于卡尔曼滤波的算法在估计精度、组合多种传感器数据的能力以及识别和拒绝错误反馈的能力等方面都受到限制。Rogers等[60]探讨了证据理论在弹丸状态估计中的应用。与卡尔曼滤波算法相比，该估计器能够处理完全非线性的动态模型，并且不作任何传感器误差统计假设。实例仿真表明，该方法的关键优势来自估计过程中识别和消除故障传感器的能力。综上可知，由于目标模型及系统控制模型本身的不确定性，在状态估计算法设计时，研究者们需更多考虑实时性及数据处理精度等基本要求。

另一方面，尽管卡尔曼滤波相关变体是目前智能武器应用中状态估计的主要手段，但在追踪高机动目标时性能仍有待提高。为了减少目标机动性对状态估计系统的影响，一些相关算法也得到了学者们的关注。最广泛使用的是交互多模型(Interacting Multiple Model，IMM)及其变体[61]。IMM使用不同的机动模型，并比较每个测量值的残差，以确定哪个模型最适合当前的行为。此外，Stubberud等[62]提出了一种最初作为目标分类方法发展起来的特征对象提取(Feature Object eXtraction, FOX)的证据累积技术，也可被用于融合卡尔曼滤波中的增益行为，并估计是否发生机动。同时，一些自适应卡尔曼滤波器，如神经扩展卡尔曼滤波器(Neural Extended Kalman Filter, NEKF)，针对高机动目标的状态估计性能极佳。Kramer[63]和S tubberud等[64-67]针对NEKF做出了大量研究，研究结果表明，存在模型误差的情况下，神经网络可改善状态估计中的耦合函数。同时，通过将NEKF应用于系统反馈回路之内和控制回路之外的两种系统辨识方案性能进行了研究对比，提出了一种基于非线性约束序列状态估计器的参数估计方法。神经网络理论在弹丸状态估计算法研究中的价值得到了初步验证。

3.2 修正机构参数优化设计算法

修正机构参数设计，作为修正弹总体设计中的一个重要环节，指在多个约束条件下选取较为理想的设计值，使其能够满足武器系统的性能要求。

早期研究中，学者们主要在设计变量极为有限的可能范围进行探讨对修正效果的影响，为修正弹设计提供一定参考，但这也导致设计过程往往需要多次迭代才能满足性能需求。Jitpraphai和Corriveau等均以脉冲修正弹为研究对象，分别讨论不同脉冲发动机参数对弹丸散布[68]及横向修正能力的影响[69]，进一步提出了理想条件下脉冲发动机参数优化方案的三条准则[70]。类似地，徐劲祥等[71]也指出，由于脱靶量效果的研究均是在单一变量的变化条件下研究所得，工程应用中需要多次优化才能确定修正机构参数设计。常思江和许诺等分别利用复合形调优法[72]和分岔分析方法[73]讨论了基于鸭舵类型修正弹的修正机构参数对弹道特性及气动外形设计的影响，但两种方法所得结果均为局部最优解。尹永鑫[43]和于剑桥等[74]在理想条件下单独对修正作用时机进行了研究，但所提出方法的根本原理仍是基于穷举策略，不适用于策略集元素较多的情况。

但实际情况中，修正机构参数的设计优化过程需要针对互相耦合的多个设计变量进行，这导致智能弹药的总体性能优化存在较大困难，而智能算法的发展为该问题的解决提供了新的思路。在早期研究中，由于穷举法的参数优化需要大量的计算时间，Burchett验证了利用遗传算法实现修正弹参数优化设计的可行性[75]。类似地，尹永鑫等[76]利用遗传算法对脉冲推力器使用个数进行了优化。Burchett[75]和尹永鑫等[76]的研究结果表明，该方法下得到的最优解可有效减小脱靶量。此外，曹小兵、常思江、李嘉、孙瑞胜等[41，77-79]均考虑用不同改进形式的粒子群优化算法的思路来解决多个约束条件下的参数的优化问题。其中，文献[41]和文献[77]均以脉冲发动机能耗最小为优化目标，文献[78]和文献[79]以双优化目标函数为基础进行了研究。Fowler等[80]则在实验设计基础上，通过神经网络识别不同参数配置方案中的不稳定设计，并利用遗传算法确定最终优化结果。尹永鑫等[81]通过改进的前馈神经网络来调整 PD控制参数，有效降低了修正弹点火逻辑控制系统耦合性，并提高了系统动态性能。滕江川等[82]则利用模糊控制理论对脉冲修正弹的点火逻辑策略进行了优化设计，研究结果表明，所提方法可显著减少推力器的使用数量，增加了机动可用过载。同时，可有效缩短系统响应时间并提高抗干扰性和鲁棒性。

另外，在弹道修正弹的优化控制算法领域，以神经网络为主，包括群智能算法等现代智能算法得到了初步的尝试和发展。但由于在线训练计算过大，实际应用过程中无法满足实时性要求，因此目前在工程应用中不具有普适意义。此外，传统的修正机构点火逻辑策略大多是在忽略多种干扰因素条件下所得，且需要的先验信息较多，因此相关算法性能仍需进一步优化。综上所述，未来修正弹优化设计过程中，应更关注算法与控制系统之间的动态反馈性能，从而有效提高弹丸解算实时性。

3.3 二维弹道修正弹制导律

3.3.1 传统非智能制导律

由于在弹丸实际飞行过程中存在大量干扰因素，因此，为提高命中精度，需要控制弹丸按照一定控制规律飞向目标。制导律设计在导弹研究中已经得到了深入的发展，而好的制导律同样也能提高低成本制导炮弹的打击精确度和作战效果。但修正弹的制导律设计，必须考虑其在应用背景及弹体结构等方面与导弹相比存在的特殊性。目前，相关领域的主要制导律有比例导引制导律、弹道跟踪(Trajectory Tracking, TT)制导律、落点预测(Impact Point Prediction, IPP)制导律和最优制导律等。同时根据控制理论对制导律进行分类，又可以分为传统非智能制导律和智能制导律。

TT制导律要求弹丸飞行过程中速度矢量始终指向目标。该方法最早发展且技术简单，但也存在需用法向过载大、不能全向攻击以及速度受限严重等缺点，因此实际应用较少[83]。比例导引制导律则是指弹丸飞行过程中，速度矢量的旋转角速度正比于目标线的旋转角速度的导引方法，比例导引制导律具有能充分利用导弹机动能力、实现全向攻击以及实现较为容易等优势，应用更为广泛。但由于比例导引制导律打击目标时所需法向过载受弹丸速度和方向影响较大，一些改进方法得到了一定发展和应用，主要包括比例导航制导(Proportional Navigation Guidance, PNG)、抛物线比例导航制导(Parabolic Proportional Navigation Guidance, PAPNG)和修正比例导航(Modified Proportional Navigation, MPN)等。

目前，不同制导律在不同类型弹道修正弹上的实现过程及修正性能得到了学者们的广泛关注。基于鸭舵式修正弹，朱大林[20]推导了TT和MPN方法下的舵指令生成过程，并指出两种方法性能对测量误差的不同敏感度，由于后者所需弹道先验信息较多，因此对测量数据误差更为敏感。Burchett等[84]以脉冲修正火箭弹为研究对象，横向比较了PNG、 PAPNG和TT方法在不同脉冲数目下的修正精度。研究结果表明，在脉冲数量较少时，TT制导律可使弹丸获得较低的落点散布及较小的脱靶量；但在脉冲数量较多时，PAPNG方法更佳。进一步，赵捍东[85]指出TT制导律对脉冲修正力过于敏感导致的工程实用劣势，以及PAPNG法存在的大射角条件下射程修正效果不佳的问题。

基于最优控制理论的制导律强调弹丸按照预定要求，在给定的目标函数下达到极值。文献[32，72，86]均以能耗最小为目标，按照剩余脱靶量最小的要求(即命中目标)，针对不同弹道修正弹最优控制问题进行了研究。尽管肯定了最优制导律可为控制算法设计提供理论参考，但也均指出该方法在求解实时性方面的不足。此外，贾正望[46]研究了针对变质心修正弹的高阶姿态控制系统而提出的基于状态相关Riccati方程的求解问题，其工作主要针对该类方程计算量大、实时性受到限制的缺点进行改进。Theodoulis和Burchet等对于二维修正弹的控制策略进行了研究，他们的研究均建立在线性变参数模型基础上，其研究也指出了最优控制策略设计方案的模型依赖性[87]和针对机动目标的局限性[88]。

另一方面，传统最优控制理论进一步发展，衍生的模型预测控制(Model Predictive Control, MPC)同样被应用于修正弹控制领域，它利用对象的动态模型将状态投射到未来，然后利用估计的未来状态来确定控制动作。Burchett和Ollerenshaw等[88-89]利用弹丸线性理论对脉冲式及鸭舵式修正弹的控制进行建模，并提出了相关的最优预测控制解。此外，Slegers对MPC控制应用于低速小口径弹药时呈现的特殊动力学特性进行了关注，研究结果表明，该预测控制策略能有效降低系统散布[90]。

落点预测制导律作为一种主要的弹道修正制导律，以最优弹道参数估计值作为输入，利用弹上处理器解算后续弹道，输出预测落点。Ilg[91]在其博士论文中指出IPP制导实施的关键就是要获得制导时刻的零效脱靶量(Zero Effort Miss，ZEM)，而计算ZEM需要在线预测弹丸的落点位置。由于在考虑系统的所有参数(如大气条件、空气密度、燃料参数等)时，数学模型会迅速卷积，因此，为满足IPP制导律实时性的要求，对保留弹丸关键参数的弹道模型的简化处理就显得尤为重要。利用弹丸线性化模型的解析解进行落点预测输出是简化弹道模型的一种被普遍采用的方法[92-95]。而为了尽量保留弹丸的非线性动力学特性，Demir等[96]通过建立弹丸的随机模型，提出了一种基于近似统计矩的IPP方法，同时该方法还可有效避开约束落点区域。IPP制导律在修正效果上独特的优势也得到了国内学者们的关注。曹小兵通过对三自由度质点弹道模型的近似求解，提出了一种通过估算剩余飞行时间预测落点的方法[41]。李超旺等则将摄动原理与IPP相结合，通过将扰动系数解算赋予地面计算机以降低六自由度方程解算时间[97]。不难发现，目前为满足IPP制导律实时性要求，研究多采用计算模型简化或改变计算硬件条件等措施。

对于以上经典制导方法，比较容易实现的是TT制导，但横向修正效果差。PAPNG方法的横向修正效果优于TT方法，但纵向修正效果不理想。当目标静止时，PNG是使用最多、性能最好的导航制导方法[20]。传统最优制导虽然可以实现某一目标性能最优，但仅适合于拦截非机动目标。而且对于非线性最优制导问题通常只能离线求解数值，尚未有比较高效的求解算法。而传统IPP方法预测精度对算法模型依赖程度较高，且目前发展受到计算机硬件限制较大。

面对复杂的非线性高维飞行动力学系统，相比于经过线性化或简化的弹道模型(如质点弹道模型、三自由度和四自由度弹道模型等)，六自由度弹道模型预测精度更高，但具有其模型复杂、计算量大、对硬件要求较高等劣势，导致计算实时性不佳成为目前传统制导律较为突出的缺点，进而导致实际作战中对机动目标打击能力的不足。由于该类问题亟待改善，因此针对不同类型修正弹，实际工程应用中往往需要平衡解算速度和制导精度之间的关系。由于制导律的改进允许修正弹控制系统在硬件不变的情况下有效降低落点散布。因此，随着模糊控制、自适应控制理论、滑模控制理论、群智能优化算法和神经网络等现代控制技术的发展，制导律的智能化发展和应用为提高传统弹药的精确打击提供了新的思路。

3.3.2 智能制导律

神经网络不依赖已有系统建模，可逼近任意属于L2空间的非线性函数，利用其学习及推广能力，对开环的数据最优制导律进行离线学习，然后作为闭环的神经次优制导律来在线应用[46]。Ghosh等[98]采用神经网络算法对基于线性拟合的传统落点预测制导律进行改进，实现了较高精度的预测控制。Kramer等的研究再次肯定了神经网络在预测控制方面的价值，改进后的NEKF更加逼近真实的动力学模型，且跟踪机动目标方面更具优势[63]。曹红锦等[99]基于质点弹道模型，选取BP神经网络和 Elman 神经网络进行神经网络弹道预测仿真，结果表明，后者预测精度较高。基于线性弹道模型，黄鑫[100]对比了BP神经网络、插值型径向基神经网络、广义回归神经网络和高维插值方法下的弹丸落点预测精度。黄鑫的研究结果表明，插值型径向基神经网络方法下的预测精度较高，但解算速度仍有待提高。针对传统滤波外推IPP法存在的不足，冯耀暄等[101]提出一种动态径向基神经网络在线辨识与带自调整因子模糊控制相结合的落点预测导引律，可有效提高系统的自适应性和鲁棒性，保证较高的制导精度。卢超群等[102]提出了一种基于神经网络的Q-learning算法，研究表明，该类方法在拦截大机动目标时具有一定优势。以上研究中，弹丸控制动态系统利用动态网络建模得以更好地反映系统内在规律。但同时，由于离线训练的神经网络对于固定条件下的弹道具有较高的精度，造成使用范围受限。因此，在面对不同被控对象时，需合理选择网络模型。

此外，与基于串行计算的中央处理器(Central Processing Unit，CPU)相比，图形处理单元(Graphics Processing Unit, GPU)作为一种功能强大的大规模并行计算设备，越来越多地被用于通用计算。鉴于IPP制导律对计算实时性要求较高，将GPU引入制导律研究也得到学者们的关注。Ilg和Rogers等基于六自由度弹道模型，将在CPU上执行的串行Monte Carlo模拟和在GPU上执行的并行模拟之间进行运行时的性能比较。结果表明，计算量较大的情况下，后者运行时间可以显著减少[103-104]。同时针对以往制导律无法处理区域约束的问题，基于GPU的随机控制制导律也被证明是有效的处理方法[105]。

滑模控制理论和自适应理论同样被应用于智能制导律设计领域。滑模控制方法设计简单，在解决参数不确定或模型非线性控制系统时具有一定的优势。王丹妮[52]以变质心飞行器为研究对象，考虑控制过程中的不确定性和修正机构的摄动，采用自适应滑模控制方法与退步法相结合，并对其鲁棒性和稳定性进行了验证。赵国宁等[106]提出一种基于终端滑模理论的自适应制导律，可使激光修正弹实际轨迹接近于预期轨迹。

航空航天其他领域也有智能制导律的应用。默朝明[47]则提出了一种基于摄动理论的IPP制导律，并在此基础上利用遗传算法得到了变质心式修正弹中滑块参数之间的关系。孙瑞胜等[107]通过在BP神经网络控制基础上混合遗传算法优化 BP神经网络反向传播权系数值，能使制导炸弹准确命中目标，并使系统具有良好的鲁棒性。王林林[108]针对再入飞行器提出了一种IPP与遗传算法相结合的制导律，提高了控制系统的稳定性。张振兴等[109]以空战飞机为研究对象，提出一种基于实时反馈的长短期记忆神经网络的航迹预测模型，可实现对轨迹的快速预测。徐寅[110]以人造卫星为研究对象，使用支持向量回归机对实测数据进行短时间趋势预测，同时使用改进后的RNN神经网络实现长期预测并达到精度指标。

3.4 控制算法展望

自弹道修正弹产生起，控制问题就受到学者们的广泛关注。随着现代控制理论和计算机技术的发展，相关控制算法的智能化发展也取得了丰硕的研究成果。

在理论研究方面，许多学者进行了较为深入的探索。但对于实现进一步的实际工程应用，以下问题值得继续研究：

1)系统建模及模型误差的深入分析。基于线性外弹道理论，目前大部分文献均采用简化的控制模型实现制导律的设计。若能对于不同类型修正弹的主要关键状态信息进行分析，就能有针对性地解决弹道修正弹的控制问题。同时，以往研究中往往直接给出噪声假设，若能不依赖系统模型，通过神经网络等自主学习方法对实际飞行弹道数据训练的逼近真实动力学特性，可有效提高控制系统的鲁棒性。因此，未来研究值得针对系统模型的构建及不同误差形成机理做进一步分析。

2)面对机动目标的状态估计及实时解算问题。目前的文献研究多在假设目标信息已知的条件下进行，同时由于修正弹的低成本设计需求，需要尽可能减小导航系统的成本，因此相关控制算法往往存在面对机动目标打击能力不足的情况。未来研究中，一方面，在弹丸状态估计环节，可通过如FOX等理论技术改善原有数据滤波器，对目标是否产生机动行为进行预先有效估计；另一方面，提高解算系统的硬件系统，诸如GPU等计算思想可在实际应用中的作为可行思路进行进一步研究。

3)神经网络理论的应用。无论是在状态估计算法设计还是在参数优化设计以及制导律控制方法研究中，神经网络在数据处理方面准确性和稳定性较好的优越性已经得到了初步验证，但是也需要大量的前期工作，比如训练神经网络模型、设计状态空间、搜索等，并且大部分研究还处于仿真研究阶段，因此具有较大的发展空间。

4 结论

弹道修正弹作为提高常规制导炮弹的有效手段，提供了对常规炮弹智能化改造的新手段。由各国修正机构发展历史可知，我国未来弹道修正弹的发展应尽量选择短期可见成效的修正机构进行研究，迅速形成具有一定威慑能力的智能化打击武器。在相关控制算法研究方面：一方面，为提高常规制导炮弹在未来战场中的生存能力，未来算法研究中，需更多考虑针对机动目标的打击，这对算法模型的设计提出了更高要求。而这一领域中，神经网络理论具有较高的研究价值。另一方面，为解决多种任务需求下的多约束非线性控制问题，提高任务灵活性，需提高相关算法性能的精度，可考虑引入如GPU等性能更为强大的计算硬件设备。同时为保证控制系统的鲁棒性，应考虑对修正机构的实际力学特性等系统约束条件予以充分考虑。因此，将智能算法应用到弹道修正技术中，使炮射弹更加智能化、精确化是未来发展的一个重要趋势。