变换器短路故障时整流发电机的暂态电流计算

侯畅武，张晓锋，黄 靖，吴本祥

(海军工程大学 电气工程学院， 湖北 武汉 430033)

在舰船直流区域配电系统中，由于直流区域配电网的低惯性和弱阻尼特性，发生直流短路故障时会迅速传导，如果不对直流故障电流加以限制，会对直流区域配电网中的设备造成严重损害，甚至导致配电系统崩溃。因此，短路电流计算可以为舰船直流区域配电系统的主动限流控制、故障诊断和保护方法提供关键性的理论依据。在舰船直流区域配电系统中，直流变换器作为连接整流发电机和逆变器或负载的核心设备，当整流发电机后端的直流变换器发生短路故障时，整流发电机的暂态电流会通过直流变换器内部的变压器馈入短路点，尤其常见于模块化多电平换流器为主的直流变换器短路故障[1-2]，短路电流必须考虑整流发电机进行计算。此时整流发电机带直流变换器运行可以等效为整流发电机突加RLC负载，容性负载的加入会导致数学模型的阶数升高，整流发电机突加RLC负载的暂态过程与突加RL负载的暂态过程有明显差异，因此本文将对整流发电机突加RLC负载的暂态过程进行分析。

文献[3]通过将直流侧负载折算到交流侧，分析了整流发电机突加阻性负载时对于直流侧电压的影响。文献[4]研究了整流发电机的时域数学模型和瞬时电磁特性，构建了整流器、同步发电机和负载模型统一的时域数学模型，但是都没有详细分析有容性负载时暂态特性。针对文献[5]中舰船电力推进系统的整流发电机—逆变器—感应电机的运行结构，整流发电机后端设备短路时等效为整流发电机突加RL负载，对此问题国内外学者进行了广泛的研究[6-8]，而对于容性负载的结构研究较少。文献[9]分析了整流发电机带阻容性负载时静态稳定性，但是没有涉及动态稳定性。文献[10-11]针对整流发电机的独立电容充电电源系统，分析整流桥换相过程中存在的三种工作模态，得到了直流平均电流表达式，研究更侧重于整流器换流期间对于直流电压电流的影响。

本文在文献[3]的基础上，针对整流发电机后端直流变换器短路时，短路电流可以等效为整流发电机突加RLC负载的暂态电流。通过对RLC负载等效折算，运用电压和磁链方程得到了整流发电机突加RLC负载的数学方程，类比同步发电机短路电流计算，得到了突加RLC负载暂态电流近似解析表达式，且主要针对暂态电流的峰值和峰值时间，从而为主动限制直流故障电流和设计相应的继电保护方法提供依据。

1 整流发电机突加RLC负载等效电路

RLC负载的基值定义为：XRB=UB/IB、XLB=UB/IBωB、XCB=UBωB/IB，其中UB、IB、ωB分别为交流电压电流及角速度基值。三相整流发电机突加RLC负载电路如图1左侧所示，图中XL=L，XC=1/C。文献[12]通过能量守恒将直流侧RLC负载折算到交流侧进行分析，在三相整流桥中折算后，RLC对应的阻值变化为xR,L,C≈0.609xR,L,C，而在十二相整流桥中则为xR,L,C≈2.432xR,L,C。其中，xR,L,C代表等效到交流侧后RLC的大小，等效过程如图1所示。

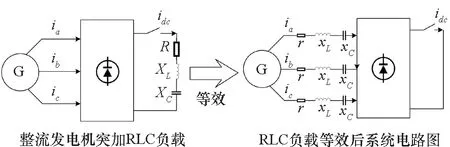
图1 发电机整流系统突加RLC负载等效示意图Fig.1 Equivalent diagram of generator rectifier system with suddenly-applied RLC load

将RLC负载等效至交流侧后，忽略整流桥换相过程，整流发电机突加RLC负载可以等效为同步发电机各相串联RLC后三相突然短路[13]，对于突加RLC负载的暂态过程分析可以等效为三相短路的暂态过程分析。

2 整流发电机突加RLC负载的暂态电流表达式计算

根据图1，基于同步发电机磁链、电压方程和电压基尔霍夫定律可以写出如下方程：

(1)

其中：p=d/dt为微分算子；uk、ik、φk(k=a,b,c)分别表示定子绕组各相电压、电流和磁链。对三相电压进行park、clark变换可得：

(2)

其中：γ为电角度，γ=ωt+θ；ω为电角速度；θ为初相角。对式(2)两边同时微分并整理可以得到式(3)和式(4)如下：

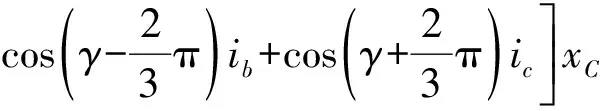
(3)

(4)

类比式(2)，根据磁链表达式和三相交流电流的表达式可以得到Φd、Φq、id、iq的表达式，微分后可以得到pΦd、p2Φd、pΦq、p2Φq、pid、p2id、piq、p2iq的表达式，并且假定没有励磁电压调节作用，就短路部分引起的变化部分而言，励磁电压为0。因此可以得到：

(5)

式中，xd(p)为d轴运算电抗[14]，xq(p)为q轴运算电抗。又有φqpω=0，φdpω=0，将上述所有表达式代入式(3)和式(4)可以化简为以下形式：

(6)

由式(6)可知，感性负载直接加至直轴与交轴电抗上共同参与运算，这与整流发电机带阻感性负载的等效数学模型[15]是一致的。对式(6)进行求解得到暂态电流的表达式如下：

(7)

其中

(8)

由于分母中方程表达式阶次过高，很难写出其解析表达式，类比同步发电机短路电流解析表达式的求解，可以通过确定暂态电流的初值、终值以及衰减时间常数来给出其近似解析表达式。

3 暂态电流解析表达式计算

由于存在感性负载，为便于计算，对同步发电机原有的交直轴运算电抗重新假定如下：

(9)

其中，x′d为d轴瞬变电抗，x′q为q轴瞬变电抗，xd为d轴同步电抗，xq为q轴同步电抗。

3.1 暂态电流的初值与终值计算

由式(7)可知，交直轴电抗与感性负载串联，且一般感性负载远大于交直轴电抗，这相当于同步发电机有较大漏抗；根据同步发电机的交直轴超瞬态和瞬态等值电路[14]可知，在漏抗较大时两者等值电路近似相等，因此可以按照无阻尼同步发电机模型进行运算。根据运算微积的初值定理，式(7)在p=∞时为该变量的起始值，此时xd0=xd1,xq0=xq1。忽略定子与转子电阻后式(7)可以近似表示为：

(10)

运用Heaviside变换[16]可以得到初值的解析表达式为：

(11)

从式(11)可以看出，在定子绕组电流中不仅含有非周期分量，还含有同步发电机基波频率和二阶电容电感谐振频率相加减得到频次的电流，一般同步发电机基波频率比谐振频率低，两者相减频次电流最终表现为衰减量，因此主要表现为两者相加频次的电流。

对于暂态电流的稳态值，根据运算微积的终值定理，运算公式在p=0时为该变量的终值，此时有xd0=xd2,xq0=xq2。在忽略定子电阻时，暂态电流的稳态值为：

(12)

可以看到初值在不断衰减后与终值吻合。

3.2 暂态电流的衰减时间常数计算

定子绕组电流含有的非周期电流分量，对应于转子绕组中基波频率和谐振频率共同作用的电流分量，在求该衰减时间常数时可以近似认为转子绕组的电阻为0，则有

A(p)=(p2+ω2)[(pxd1+r)(pxq1+r)+ω2xd1xq1]+

xC[(p2-ω2)(xd1+xq1)+2pr+xC]=0

(13)

该方程为一元四次方程，求解一元四次方程ax4+bx3+cx2+dx+e=0的解，可以近似得到定子非周期电流衰减的时间常数为：

(14)

同理，定子绕组中基波频率和谐振频率共同作用的电流分量对应于转子电流中的非周期电流分量，在求该衰减时间常数时可以近似认为定子绕组的电阻为0，则有

A(p)=(p2+ω2)2xd1xq1+

(15)

因此该衰减时间常数为：

(16)

考虑同步发电机空载时，利用叠加原理，三相突然短路相当于加上与空载电压相等、方向相反的电压，因此，将ud=0、uq=-E代入式(11)～(12)后可以得到解析表达式为：

(17)

通过式(17)可以得到三相电流的表达式及暂态电流的峰值时间与峰值大小[17]为：

(18)

(19)

转换到直流侧以后，十二相整流发电机[18]直流电流的峰值为：

idcmax≈3.831iφmax

(20)

由式(17)～(20)可知，同步发电机的运行状态此时主要取决于交直轴瞬变电抗和同步电抗，感性负载和容性负载匹配度对于直流电流的峰值和峰值时间都会产生较大影响。通过上述直流电流的峰值与峰值时间的表达式，对于确定直流变换器主动限流控制方法和系统继电保护方法是具有重要意义的。

4 仿真验证

采用十二相整流发电机在PSCAD/EMTDC环境中进行仿真试验验证，表1给出了其中单台三相同步发电机的参数。

表1 同步发电机参数

表1中p.u.表示标幺值大小。十二相整流发电机在空载状态时，于0.03 s突加RLC串联负载；其中R=0.001 Ω,L=1 mH,C=100 μF，直流电流仿真波形如图2所示。

图2 十二相整流发电机突加RLC负载电流波形Fig.2 Current waveform of 12-phase rectifier generator with suddenly-applied RLC load

从图2可以看到暂态电流为正弦衰减变化，与理论解析表达式的分析可以保持一致。

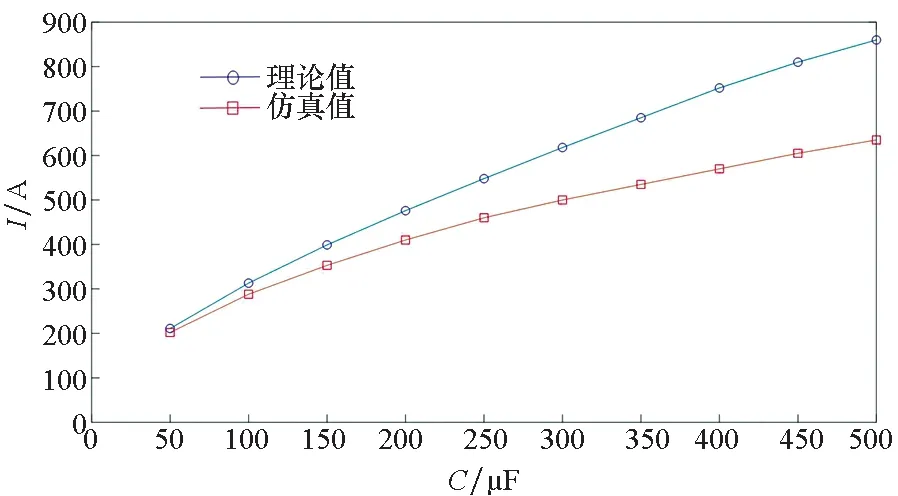
图3 直流电流峰值随电容变化的理论值与仿真值 Fig.3 Theoretical and simulative value of direct current peak as the capacitance changes

图3给出了负载在电容不同而R=0.001 Ω,L=1 mH恒定时，直流电流峰值的理论值与仿真值变化图。图4同时给出了负载端在电感值不同而R=0.001 Ω,C=100 μF恒定时，直流电流峰值的理论值与仿真值变化图。

图4 直流电流峰值随电感变化的理论值与仿真值 Fig.4 Theoretical and simulative value of direct current peak as the inductance changes

可以看到，在电容或电感逐渐变大后，直流电流峰值下降速度会逐渐变慢最终趋于一个稳定值，且随着电容或电感值的增大，直流电流峰值的理论值与仿真值偏差也越来越大。

分析可知，引起直流电流峰值理论值与仿真值产生误差的原因主要有两个方面：

1)暂态电流达到峰值的时间并不是固定值，因此暂态电流峰值表达式中第一项会根据衰减时间常数T以及峰值时间Tpeak出现不同程度的衰减，文中由于计算得到的时间常数T较为复杂，因此在暂态电流峰值表达式中并没有添加衰减系数，从而导致理论值大于仿真值。

2)文中在计算暂态电流表达式中只使用了同步发电机交直轴瞬变电抗，而没有使用超瞬变电抗，主要是由于超瞬变衰减极快，衰减时间常数很难用公式表达，因此使用了同步发电机交直轴瞬变电抗进行计算会产生偏差。

从继电保护和实际工程应用的角度来看，暂态电流理论值计算偏大，系统保护的冗余量也会相对偏大，能够提高系统稳定性。

图5和图6给出了在不同电感值时直流电流峰值随着电容变化的曲线图和在不同电容值时直流电流峰值随着电感变化的曲线图。

从式(19)中可以看到，随着电容的增大，xC相应变小，暂态电流峰值就会变大；电容固定而电感不断增大时，暂态电流峰值变化率会逐渐减小；这与图5中的变化趋势是一致的。随着电感的增大，xL相应变大，暂态电流峰值会变小，电感固定而电容不断增大时，暂态电流峰值表达式中后一项下降速率比前一项的增长速率逐渐加快，暂态电流峰值下降速率会越快，这与图6中变化趋势是一致的。

图5 不同电感下直流电流峰值随电容变化的曲线图 Fig.5 The graph of direct current peak under different inductance as the capacitance changes

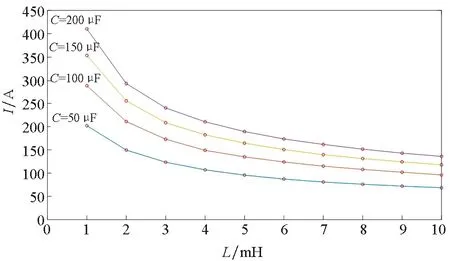
图6 不同电容下直流电流峰值随电感变化的曲线图Fig.6 The graph of direct current peak under different capacitance as the inductance changes

表2和表3分别给出了不同电容、电感情况下峰值时间的理论计算值与仿真实际值。

表2 不同电容值时峰值时间理论值与仿真值结果

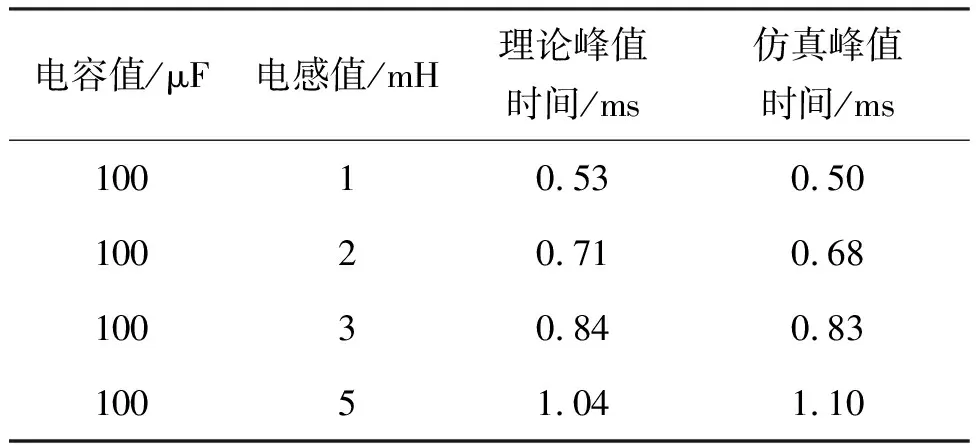
表3 不同电感值时峰值时间理论值与仿真值结果

根据式(17)、式(18)可以看到，在电容值变大时，暂态电流的频率会变小，到达峰值时间会变长；而在电感值变大时，暂态电流的频率也会变小，到达峰值时间变长；理论值与仿真值存在误差主要是由于仿真步长等因素导致读取存在误差。从表2和表3中可以看到，随着电容或电感不断增大，峰值时间理论值和仿真值都逐渐增大，这与式(18)的理论分析是可以吻合的，因此暂态电流频率为同步发电机基波角频率与同步发电机交轴瞬态电感与突加电感之和以及突加电容的谐振频率组成，这两者的均方根为暂态电流频率。

5 结论

本文针对舰船直流区域配电系统中直流变换器侧短路故障时，整流发电机带直流变换器运行可以等效为整流发电机突加RLC负载。本文在对RLC负载进行了等效折算后建立了同步发电机电压和磁链方程，推导出了暂态电流表达式；参照同步发电机短路电流计算方法，得到了暂态电流的近似解析表达式。不同于整流发电机突加阻感性负载或容性负载，整流发电机突加RLC负载的暂态电流频率为同步发电机的基波角频率与电感、电容谐振频率的均方根，不再为固定值，且会随RLC负载的状态发生改变；暂态电流峰值会随电容增大而上升，随电感增大而下降。最后，针对直流变换侧短路状态下整流发电机的短路电流，给出了电流峰值以及峰值时间并通过仿真验证了本文理论分析的有效性。但是由于衰减时间常数无法完整进行表述，本文中电流峰值计算没有考虑电流衰减，因此通过物理模型的等效回路来模拟得到暂态过程衰减时间常数是下一步的研究方向。