基于隐藏子空间的量子货币的攻击研究*

胡志泉 ，薛 立 德 ，杨 威

（1.中国科学技术大学 计算机科学与技术学院，安徽 合肥230026；2.中国科学技术大学 苏州高等研究院，江苏 苏州215000）

0 引言

随着量子密钥分发（QKD）[1]的应用，量子密码协议正处于蓬勃发展的阶段，但是作为最早出现的量子密码学问题之一，量子货币问题尚未得到适当的解决。由于很难长时间维持量子态的相干性，并且在量子货币方案中，伪造者可以在验证算法提示下获得有关未知量子态的更多详细信息，因此量子货币方案通常需要更严格的安全证明。量子认证，尤其是量子签名，与量子货币有潜在的联系，量子货币本身可以被视为一种特殊类型的量子签名。量子货币方案各种变体还可形成具有不同功能的量子密码协议，现有量子签名协议，例如ZMWZ协议[2]、文献[3]所提协议以及基于相位编码的协议[4]都基于QKD技术，因此量子货币方案的研究将带来量子签名的新方向。

1 量子货币方案的内容和概况

1.1 量子货币的研究背景

量子货币的概念最初是在1969年提出的，其主要目的是允许银行发行不可伪造和可验证的量子货币态。随后，Wiesner提出了第一个私钥量子货币方案[5]，该方案由产生钞票（量子货币态）的银行和验证钞票真实性的验证算法组成。虽然在信息理论上已被证明是安全的，但后来发现它存在许多安全缺陷-“验证问题”：由于其作为私钥量子货币方案的性质，只有生产钞票的银行才能验证其真实性；“数据库问题”：银行需要为其发行的每张钞票存储一个经典描述（1983年，Wiesner[6]等人使用伪随机函数解决了“数据库问题”，并将原始方案变成了计算安全的方案）；“攻击问题”：有很多有效的攻击方案，例如 Lutomirski的“在线攻击问题”[7]，Nagaj等人的“自适应攻击”[8]等。 在最初的私钥方案之后，由Aaronson[9]提出的公钥量子货币方案引起了很多关注，它的核心思想是公开验证算法，以便每个人都可以验证钞票的真实性。随后，Farhi等提出了基于结的量子货币方案[10]，其钞票是具有相同亚历山大多项式的编码状态的叠加。尽管到目前为止尚未发现对该方案的有效攻击，但也没有证明该方案是安全的。Aaronson和Christiano随后提出了一种在隐藏子空间上基于公钥的量子货币方案[11]，并证明了它的计算安全性，他们构建了安全的微型量子货币方案，并将其与数字签名相结合，以防止量子选择明文攻击。虽然该方案存在一些缺陷（将在第2.1节中讨论该问题），但仍提出了许多有用的建议，Aaronson等表明量子货币由于其无纠缠的性质而具有很高的实用性。 但是，随着诸如“量子态恢复[12]”之类攻击算法的出现,大多数当前的量子货币方案可以被有效攻击，尤其是无纠缠的量子货币方案，其根本是许多无纠缠的方案，它们的验证算法由秩为1的投影测量构成，因此对于量子货币，纠缠方案受到更多关注。在实验领域，Bartkiewicz[13]首先通过实验重新审视了Wiesner的想法，表明可以使用量子态制备无法真实克隆的钞票，Bozzio[14]的实验也朝着实现量子货币迈出了关键的一步。如上所述，量子货币问题尚未完全解决，面临的最重要挑战之一是计算安全性不充分，原因之一是大多数安全性建立在伪造者应使用方案提供的预言黑盒（oracle）的假设，这可能会限制伪造者的攻击手段，所以量子货币方案需要更深入的研究。

1.2 量子货币的一般方案

一个通用量子货币方案S由两个主要部分组成：银行和验证算法（Ver）。银行每次都会使用经典密文〈x〉来制造 Ver接受的钞票，其中〈x〉可以是真正的随机、伪随机或特殊含义的字符串，Ver可以是酉或非酉操作。给出以下简要定义：

（1）银行：接受经典密文〈x〉，并从〈x〉准备量子货币态 |〉（有时还准备一个经典序列号）。

（2）Ver：接受输入的钞票并输出“Accept”=1或“Reject”=0。

对于任何伪造者C，假设C的可用资源为：一张或多张目标钞票，多次调用Ver的能力，验证后的量子态的检索和多项式量子计算能力。令|1〉=|2〉=…=|q〉（q≥1）分别为存储在 q 组寄存器中的q张相同的目标钞票，而|Σ〉是 C的辅助态。C的所有输出态都存储在h（h≥1）组寄存器中。令：

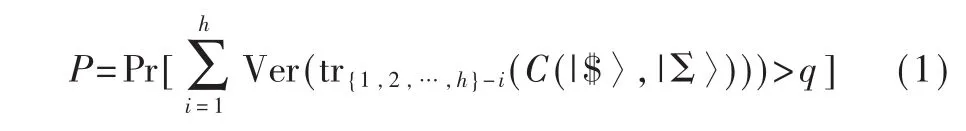
2 攻击隐藏子空间方案

本节将重点介绍A＆C的隐藏子空间方案，并详细说明其中的一些安全漏洞，以及利用这些漏洞的攻击算法。

2.1 安全缺陷

A＆C方案的核心是隐藏子空间微型方案，其定义如下：

然后矩阵Λ为：

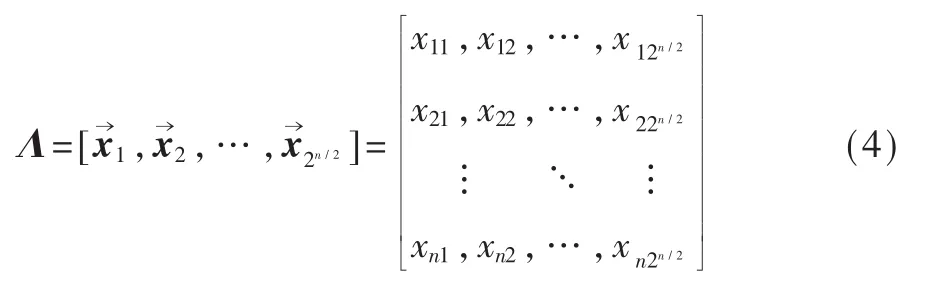
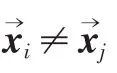
当 rank（Λ）=n/2时，存在满足的矩阵 Λα和 Λβ：

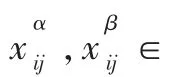
算法1获得集合R

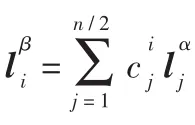
输出：集合 R

1:初始化 R=Ø

5: else

12:end if

13:end for

其元素Ri也是子空间A的集合，并得到定理1。

定理1根据算法1获得的集合R具有以下性质：

（1）A&C方案的每个量子货币态都可以写成：

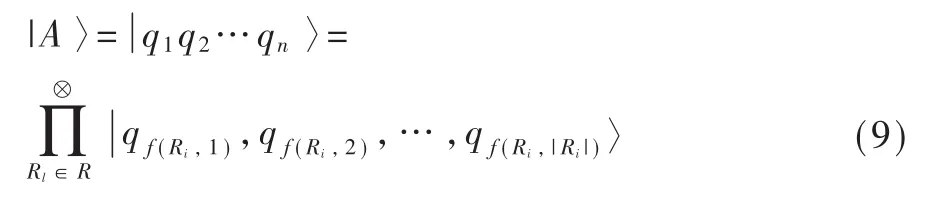
其中 f（Ri，j）代表 Ri在矩阵 Λ 中的第j个元素的原始位置 （例如当矩阵Λ不执行行交换操作以获得Λα和 Λβ时，Ri的第j个元素所在的 Λ 的行数）。

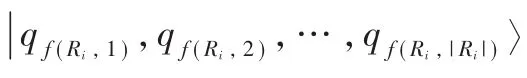
证明：考虑密度矩阵

其中，ai是长度为|Rh|的位串，bi是长度为（n-|Rh|）的位串,1≤h≤|R|。

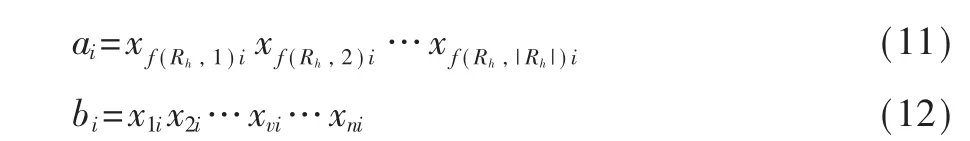
其中，v∉{f（Rh，l）|1≤l≤|Ri|}。

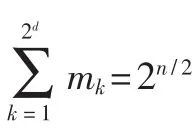
定理1揭示了由微型方案构造的量子货币态具有一定的规律性，这些规律性将成为攻击方案的主要基础。

2.2 微型隐藏子空间方案的攻击算法

对于子空间比较简单的情况，同时假设具有如下属性的伪造者：

（1）足够的计算能力（不需要是指数级）；

（2）数量大于等于1的目标量子货币态的副本；

（3）调用 Ver或 UA的次数远小于 Ω（2n/4）。

那么使用如下算法2就可以成功获取目标态的所有经典密文。

算法2微型隐藏子空间方案的攻击

输入：微型子空间方案中一些目标量子货币态的副本|A〉；

预估的纠缠量子比特的最大数量：maxR=maxRi∈R|Ri|。

输出：|A〉的经典密文。

1: 初始化集合 γi，i∈{1，2，…，maxR}，令其为的一组组合数，e.g.，γ2={（1，2），（1，3），…，（n-1，n）}，γ3={（1，2，3），（1，2，4），…，（n-2，n-1，n）}，… ，是 γi中的第i个元素

2:初始化计数器i=1和集合S=Ø

3:对目标量子货币态的副本（副本数≥1）在标准基下测量,获得一组线性无关的结果Z：

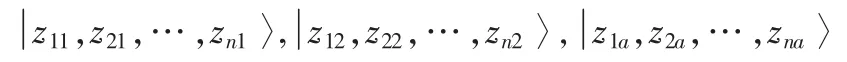
14：算法失败（但对算法 5来说，仍然产生了有用的输入）

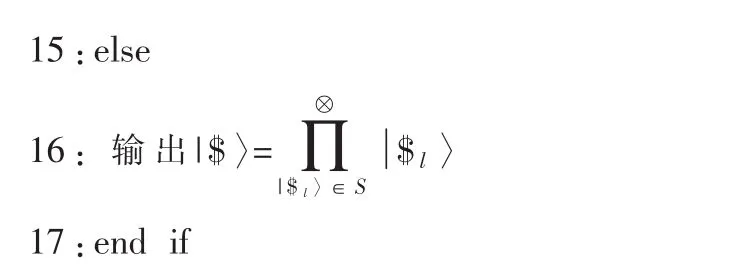
攻击算法2的核心思想是在一个标准基上测量目标量子货币态，然后使用试错法来逐一攻击量子货币的子系统，并注意该过程不会消耗任何量子货币,同时由于|Ri|相对较小，计算复杂度很低。将定理1与先前的测量结果结合起来，分析可能的情况并将其输入到UA中进行验证。

算法 2中集合 γi和 S用于存储量子位之间的关系，调用算法3来检测每个可能的关系，最后如果算法成功运行，则得到输出的目标态的经典密文。

算法3纠缠检测

输出：0 或者（1，|S〉）

1:计算下面向量集的维度d

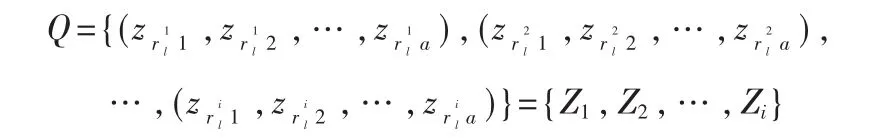
2:初始化计数器m=d和集合g=Ø假设 Zu={Zu1，Zu2，…，Zud}⊆Q 是 Q 的最大线性无关向量组

3:for m≤i do

4: 假设 Zv={Zv1，Zv2，…，Zvd}⊆Q，Zw={Zw1，Zw2，…，Zwd}⊆Q，Zu∪Zv=Zu∪Zw=Zv∪Zw=Ø

5: for each Zvdo

Zu是其一组基，并且令 Zu∪Zv是另一组行向量，这些向量可以通过Zu的元素进行线性组合。

令 Zu¯=MZu（此 处 Zu或 Zu¯也 代 表 由 集 合 Zu或 Zu¯构成的矩阵），其中M是系数矩阵，因此M可以分为 A和 B两部分，并满足 Zv=AZu，Zw=BZu。这样划分的原因如下，假设目标量子态为：

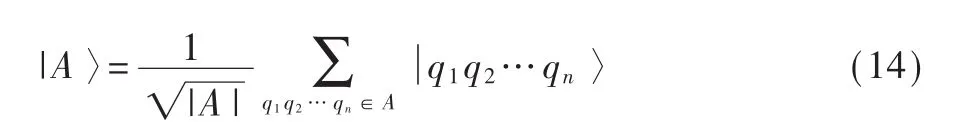
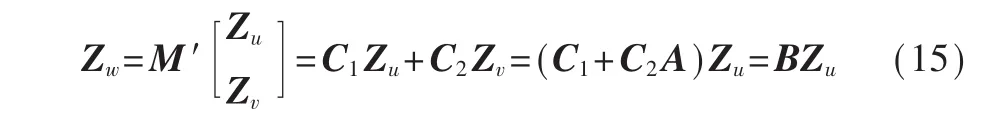
算法4更新集合γi

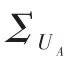
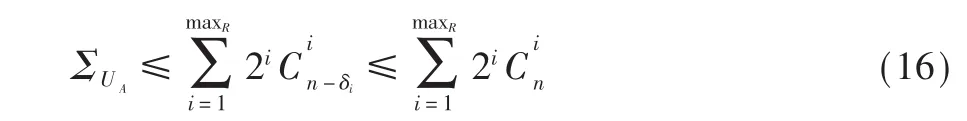
其中 δi是在算法 2的步骤（4）的前 i-1个回合中添加到集合S中的量子比特数（即已被算法2破解的量子比特数），并且如果δmaxR+1=n，则算法 2成功。可以看出，不仅与 n有关，而且与maxR有关，并且不再随n的增加而呈指数增加。当maxR足够小时，。从以上分析可以看出，对 UA的调用与所需副本之间没有直接联系。副本的数量主要影响算法3的执行速度，即伪造者拥有的副本越多，算法3的执行速度就越快。另一方面，它还显示了以下定理2与文献中的定理20[11]相反。

定理2对于具有足够计算能力的对手，即使：

（1）他只有一份未知量子货币态的副本；

（2）UA的调用次数受到限制（远远小于Ω（2n/4））。当maxR足够小时，他仍然可以成功地攻击微型隐藏子空间方案。

根据微型方案的定义，构成量子货币态的子空间A应该以相等的概率随机选择，但是现在看来，不同的子空间具有不同的安全性，量子位之间的纠缠越复杂，该方案就越安全。

2.3 微型隐藏子空间方案的扩展攻击方案

攻击算法的成功之处在于与maxR的值直接相关。当maxR太大时，攻击算法无法破解所有量子货币的经典信息，尤其是那些具有较大|Ri|的信息。但是某些子空间中的隐患远不止算法2。例如n=10，而量子货币态可以写成：

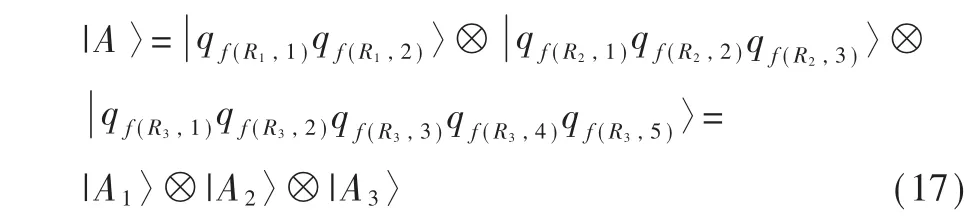
其中:

如果算法 2预设 maxR=3，因为|R3|＞3，所以无法获得与R3相对应的态。但是|A1〉和|A2〉可以被破解，可以推断出与|A3〉对应的向量空间的维数为2。接下来只要获得目标量子货币态的几个副本，并在标准基上对其进行测量，即可得到空间A3的另一结果（其中一个已在算法2中获得），然后可以知道|A3〉的所有经典信息。

上面的示例显示了从算法2派生的潜在攻击方案。即使先前的攻击算法失败，有关已破解的未知态的信息也对后续攻击有用。当|Ri|很大，但是向量空间的维数很小时，它仍然面临着非常严峻的安全风险。关于该攻击方案更正式的描述在算法5中给出。

算法5扩展攻击方案

输入：微型子空间方案中一些目标量子货币态的副本|A〉；算法 2的输出。

输出：|A〉的经典密文。

1:假设算法 2没有破解目标态的第q1，q2，…，qm个量子比特，其他破解的态记为|A1〉，|A2〉，…，|Ak〉,其中 dimAi=di，i∈{1，2，… ，k}

2:伪造者在标准基下测量所有其拥有的目标态的副本,所有线性无关的测量结果保存在I中

4: 算法失败,然后结束

5:else

6: 取I中所有元素作为基向量，在所有可能的线性组合上迭代，使τ成为这些结果的集合

3 隐藏子空间方案的改进

前面的算法仅对满足要求的子空间有效。本节将改进原始的隐藏子空间方案，并从信息论的角度为安全性提供新的证明。

3.1 改进的方案

其中A满足两个条件：

（2）态|A〉的每个量子位相互纠缠（即 A的 R集满足|R|=1）。

根据以上定义，量子货币态的结构被固定为n量子比特纠缠的纯态。虽然子空间的选择是有限的，但纠缠可以带来优势。

首先，将潜在的攻击方案分为两类：

（2）整体攻击：与部分攻击相反，如在图1中，ρA=|A〉〈A|和 trA（So）=ρA。

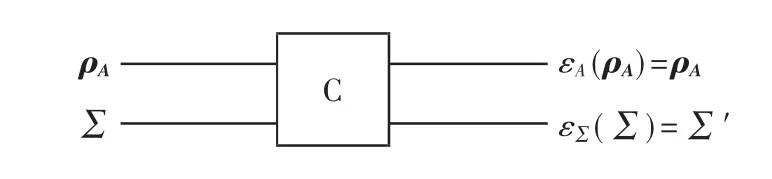
图1 伪造者潜在攻击的一般模型

算法2和算法5都属于部分攻击。在这里，攻击的分类并不限制伪造者的操作，而在A＆C的方案中，它隐含了对伪造者只能使用单一操作的限制。这就是本文改进攻击方案行之有效的原因。

3.2 安全性证明

首先给出一些量子信息论中的引理，将在后面使用。

引理1（纠缠和负条件熵[15]）假设|AB〉是复合量子系统AB的纯态，则|AB〉当且仅当条件熵S（B|A）＜0时才纠缠。

引理2假设存在一个纠缠的纯态ρ，其复合系统为 AB。 令 trB（ρ）=ρA，trA（ρ）=ρB，不存在量子算符 ε能使得 ε（ρA⊗ρB）=ρ。

根据引理2可以推断出，如果伪造者C想要使用部分攻击，则 ρA⊗ρA和 ρB⊗ρB在图 1中 C线路的任何阶段都不会存在。如果C的攻击线路有效并且线路上出现 ρA⊗ρA和 ρB⊗ρB，则线路的量子运算必然与引理2矛盾。

引理 3在图 1中， 量子算符 εΣ不能使 ρA与 Σ纠缠。

将引理2和引理3结合在一起，可以得出关于改进方案的安全性的重要结论。

如果C要通过部分攻击来克隆钞票，引理2表明，在图1的C线路中的任何阶段都不会出现ρA⊗ρA和 ρB⊗ρB，即 C 输出的复合态不能写成张量积的形式。因此，它必须是一个纠缠态，这与引理3相矛盾。引理 3也表明，量子算符 εΣ不能使 ρB与 Σ纠缠。

以上结论表明，在图 1中，trA（So）≠ρA，更进一步，根据引理 2，trA（So）≠ρB，即伪造者不能通过输入目标量子货币态的部分态来破解改进方案（该结论仍然适用于多个系统）。

对于整体攻击，A＆C的证明已经足够（也适用于本文改进的方案）。为了测量整个量子货币态以了解经典密文，他们通过限制具有相同经典密文的纸币的流通来解决了这个问题。

4 结论

本文通过理论分析,证明了A＆C量子货币方案的子空间结构存在漏洞,并非所有的子空间都绝对安全。由大量子空间产生的量子货币态可以由多个纯态子系统的直积表示，每个子系统的量子比特数量要比整个系统小得多。设计算法演示的攻击方案具有如下特点：

（1）量子货币态的副本数：本文的算法可以执行最少一个副本。它不影响算法的成功率和对Ver（或UA）的调用次数。在这里副本数影响算法的计算复杂度。

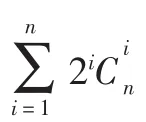
通过在子空间上添加约束改进了原始的隐藏子空间方案,确保了每个量子货币子空间结构的健壮和复杂，并且确保每个量子位之间必须存在纠缠。最后，从信息论角度看，如果伪造者想要克隆未知的量子货币，那他必须开始从整个系统进行攻击，而不是像以前那样攻击子系统。在这种情况下，伪造者将面对原始A＆C方案的完美安全性。