多变量公钥密码进展

韩益亮

（武警工程大学 密码工程学院，陕西 西安710086）

0 引言

近年来，量子计算理论与量子计算机不断取得新的进展，现代公钥密码面临的威胁日益严峻。由于对抗量子密码的迫切需求，在2006年比利时召开的第一届国际抗量子密码学会议上，多变量公钥密码、基于格的密码、基于纠错码的密码和基于散列函数的签名等被作为抗量子攻击的候选方案。相比于其他抗量子密码，多变量公钥密码的研究起步相对较早，现已有较多成熟的多变量公钥密码算法。多变量公钥密码的安全性是建立在有限域上多元非线性方程组的求解问题上的。该问题的最普通形式即：求解在只有两个元素的有限域上的二次方程组，这被证明是一个NP困难问题。在这个问题的求解上，量子计算机比起传统电子计算机也并没有明显的优势，多变量公钥密码可以良好地抵抗量子计算。它相比于其他抗量子密码具有加解密速度快、消耗资源少的优良特点，但是其公钥尺寸一般较大。

1 多变量公钥密码研究现状

多变量公钥密码系统[1-3]的研究，最早在1984年Ong和 Schnorr发表的文章[4]中就有所涉及。而从完整体制的角度来讲，文献[5]提出的MI（或称为C*）加密体制才算是真正意义上的多变量公钥密码系统，MI方案的提出开启了多变量公钥密码研究和发展的大门。

虽然在1995年，Patarin提出的线性化方程攻击攻破了MI体制，但在此之后又产生了很多新方案。1996年Patarin在攻破MI方案后，提出了隐藏域方程（Hidden Field Equation，HFE）方 案[6]， 但 是 紧 接 着HFE方案又被Kipnis和Shamir[7]分析证明不安全。于是，1997年Patarin利用线性化方程攻击的思想，设 计 了 油 醋（Oil-Vinegar，OV）签 名 算 法[8]。 然 后 ，Kipnis和Shamir用油醋分离方法攻击了OV方案，并进一步改进OV方案提出了不平衡油醋（Unbalance Oil-Vinegar，UOV）方案[9]。只要参数选择合适，UOV方案将会是一个安全的多变量签名方案。另一方面，研究人员通过各种变形的方法，如加方法、减方法以及内部扰动方法，对 MI、HFE方案进行了改进，提出了很多安全性得到提高的新方案，这方面比较著名的变形方案有：SFLASH签名方案[10]、Rainbow 签 名 方 案[11]、PMI（Perturbated MI）[12]、PMI+[13]、HFE±[6]、HFE-[6]、IPHFE（Internal Perturbation of HFE）[14]、HFEv[9，14]以及 Quartz[15]等。 这些年来，无 论是 国 内还是国外的学者，针对多变量公钥密码的核心映射构造问题，又提出了很多新方案，如2012年Huang等人通过研究新的多变量二次假设提出了可证明安全的多变量加密方案[16]；2013年 Yasuda等人提出了用二次型构造的多变量签名方案[17]，Gao等人[18]提出了以求解多项式环上diophantine方程为基础的多变量密码系统，Tao等人以矩阵构造核心映射提出的 Simple Matrix[19]方案，Shen等人提出基于身份的多变量密码方案 IBUOV[20]，Yasuda等人提出私钥更短的 Rainbow方案[21]；2014年 Zhang等人提出新的扰动方法构造的 MI签名方案[22]，Yasuda等人提出的NT-Rainbow[23]以及使用稀疏私钥的新Rainbow变种方案[24]，Ding等人提出的 Cubic Simple Matrix方案[25]以及 Porras等人提出的 ZHFE方案[26]等。到目前为止，虽然新方案很多，但是根据它们构造的特点，主要可以归纳为以下四种体制：MI体制、隐藏域方程组（HFE）体制、平衡油醋（OV）体制和三角体 制（Triangular Systems，TS，包 括 STS），具 体 将 在 下一章节将进行介绍。

当然，除了以上针对核心映射构造所做的工作以外，还有对多变量公钥密码的密码攻击分析研究，比较常见的攻击方法大致可以分为两种类型：结构攻击和直接攻击。结构攻击方法主要是线性化方程攻击、高秩攻击[27]、低秩攻击[28]、分离油醋攻击[8]、差分攻击[29]、Kipnis-Shamir攻击[7]、扩域结构攻击等；直接攻击方法主要是穷举搜索、解非线性方程攻击[30]（包括 XL 算法和 Gröbner基算法）、Zhuang-zi算法[31]等，其中秩攻击、差分攻击和解非线性方程攻击都已经是比较成熟的攻击方法，是研究人员分析新方案是否安全的有效手段。另外，对多变量公钥密码系统的攻击，除了利用结构攻击、直接攻击两种方法以外，结合以上几种具体方法也能起到很好的作用，如Wolf等人利用多种攻击相结合的方法攻破了STS、TTS方案[32]，所以这也是分析多变量公钥密码方案的另外一种有效手段。另一方面，为了说明多变量密码系统的可用性，安全问题是第一个需要考虑的问题，而除了一般的攻击分析之外，借助合理理论假设证明方案的安全性也是一种很重要的研究方法，所以在安全性分析中还可以用到形式化安全证明的相关理论。

2 多变量密码基础知识

2.1 有限域上多元多项式方程组

（1）多元多项式方程组的一般形式

设有限域 F=GF（q），x1，x2，…，xn是其中的 n 个变量，关于n个变量的任意一个多项式可以表示为f1，多项式的次数为d，一个多项式组可以由m个这样的多项式构成，以 F 表示：F:=（f1，f2，…，fm）。 其中fi=∑aj∏xj，1≤j≤m，1≤j≤n。

以 y1，y2，…，ym表示 F上的 m个元素，则有限域上的多元多项式方程组可以表示为：

（2）二次多变量多项式方程组

当上文中的d=2时，则称为二次多变量多项式方程组，一般形式如下：

其 中 x1，x2， … ，xn∈F，y1，y2， … ，ym∈F，ai，j，k∈F 为二次项系数，bi，j∈F 为一次项系数，ci∈F 为常数项。

（3）MQ问题与IP问题

定义MQ问题：给定一组有限域F上的含n个变量，m个多项式的二次多变量多项式方程组，其结构 式（2）所述 ，由 一 组 已 知 的 y1，y2，… ，ym∈F 及方程变换，求解出一组解 x1，x2，…，xn∈F以满足方程组。

1979年Garey和Johnson证明了在二元域上的MQ问题是 NPC问题，Patarin等[33]于 1997年证明了任意域上的 MQ问题是 NP完全问题。即由 y1，y2，…，ym∈F及方程变换等信息得出方程组的解在计算上是不可行的。2016年Szepieniec A和Ding等人通过取消扩展域（EFC）介绍了MQ公钥加密体制的新的中心陷门，它允许加密与签名。2017年，Szepieniec等人实现将MQ签名应用于PKI中。

定义IP问题：设F和P是给定有限域F=GF（q）上包含m个多项式和n个变量的随机多变量二次多项式方程组，在有限域F上寻找两个可逆仿射变换 S∈Fm×∈Fm和 T∈Fn×∈Fn，使 F和 P满足关系：F=S◦P◦T，则称寻找这两个可逆仿射变换的问题为IP问题。

2.2 多变量公钥密码的一般构造

多变量公钥密码系统通常是建立在庞大的代数结构之上，设F=GF（q）为有限域，则其公钥为一组有限域F上的多变量多项式方程组构成Φ：Fn→Fm

其具体陷门构造方式如图1所示。

图1 陷门构造方式

公钥Φ可以看作是三个映射的合成Φ=L1◦Φ◦L2。L1和 L2为域 F上随机选取的可逆仿射变换，其作用是将中心映射Φ′的结构隐藏起来，中心映射Φ′同样由一组n个变量m个方程的多变量多项式方程组构成。则多变量公钥密码系统的私钥为三元组（L1，Φ′，L2），一般情况下映射 Φ′保 密，也可以 公开；公钥为 Φ（x1，x2，…，xn）=（f1，f2，…，fm）。

加密过程：对给定消息 x1，x2，…，xn加密，可得到 密 文 y1，y2， … ，ym，对 应 每 一 个 yi，有 ：yi=fi（x1，x2，…，xn）。

映射Φ是公开的，则每个人都能完成对消息的加密。

解密过程：解密过程是加密过程的逆，即求Φ-1，通过私钥信息可以很容易得到 Φ-1，则（x1，x2，…，xn）=Φ-1（y1，y2，…，ym）。

由于此过程当中涉及用户私钥，则解密只能由持有私钥的用户来完成。

在多变量公钥密码系统当中，核心映射Φ′的设计是关键，其安全性主要依赖于核心映射的安全性。为了更好地在实际中应用，一般将核心映射选定为二次的，以节省存储空间。仿射变换L1和L2的应用分别用来隐藏中心映射的结构和明文信息。

2.2.1 双极系统

目前的多变量密码方案可分为双极（bipolar）系统和混合（mixed）系统，双极系统设有限域F=GF（q），在一个双极多变量密码系统当中，公钥为Fn→Fm的映射Φ：

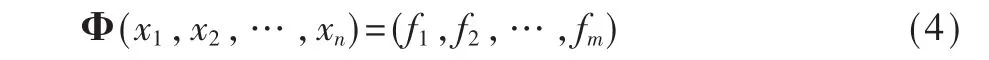
其中 f1为 F[x1，x2，…，xn]中的 n 元多项式。

其中心映射为Φ′，构造过程如下：

（1）Φ ′（x′1，x′2， … ，x′n）=（f′1，f′2， … ，f′m）， 其 中f′i∈F[x1，x2，… ，xn]；

（2）对 于 映 射 Φ′（x′1，x′2， … ，x′n）=（y′1，y′2， … ，y′m）的计算可以很容易解决，相应地也可以快速地找 到（y′1，y′2， … ，y′m）对 应 的 唯 一 原 象（x′1，x′2， … ，x′n），即 Φ-1（y′1，y′2，… ，y′m）。

在这里Φ-1仅意味着求解原象，并不是说对Φ′求逆，即Φ′并不一定是可逆的。一旦找到符合要求的中心映射 Φ′，随机选取合适的仿射变换 L1和 L2，就可以构造出一个双极多变量公钥密码方案。

双极系统的公钥包括两部分：一是有限域F及其域结构，二是映射Φ的m个多项式。私钥为随机选取的仿射变换 L1和L2，以及中心映射Φ′。

加密过程：需要加密的消息为 X=（x1，x2，…，xn），将消息值代入公钥多项式，计算得到密文Y=Φ（X）=（y1，y2，…，ym）。

解密 过 程：密 文消 息 为 Y=（y1，y2，… ，ym），对 其解密即为求解方程：Y=Φ（X）。

首先求解 L1-1（Y）=Y′，然后计算 X′=Φ′-1（Y′），再计算明文 X=L2-1（X′）。

签名过程：设需要签名的消息为Y，则需求解方 程 Y=Φ（x1，x2，…，xn）， 以 得 到 方 程 的 解 X=（x1，x2，…，xn），X为签名信息，即将解密的过程运行一次。

签名验证：将消息的签名信息代入公钥多项式，即可得到验证。

双极系统的主要思想是以仿射变换L1和L2来以隐藏中心映射Φ′，若没有这两个仿射变换，则核心映射的安全性将会受到威胁。当前，多数多变量密码体制都是基于双极系统设计构造的。

2.2.2 混合系统

同样，混合型多变量公钥密码系统的公钥也是在有限域下的映射，使用 Fn+m→Fl的映射，记为 H：

其 中 hi∈F[x1，x2，… ，xn，y1，y2， … ，ym]。 与 双 极 系 统一样，要构造一个这样的加密方案就需要找到相应的中心映射 H′：Fn+m→Fl。

中心映射要满足：对于任意给定的 x′1，x′2，…，x′n,方 程 组 H′（x′1，x′2， … ，x′n，y′1，y′2， … ，y′m）=（0，…，0）都很容易求解，并且在多数情况下，是一个关于变量 y′1，y′2，…，y′m的线性方程组。

找到符合要求的中心映射后，Φ可以表示为如下的形式：

其中L1和L2的定义与上一小节中的定义相同，L3则是一个从 Fl到Fl的线性映射。

混合系统的公钥由两部分组成：（1）有限域F及其域结构；（2）构成核心映射H的多项式方程。

混合多变量公钥密码系统的加密解密以及签名等过程与双极系统类似。其主要思想是利用三个仿射变换 L1、L2和 L3来隐藏方程 H（X，Y）=（0，…，0）。目前，基于混合系统的多变量公钥密码方案比较少，较为著名的有Patarin提出的Dragon加密体制。

3 多变量密码的几种陷门构造技术

本小节针对几种常见的陷门构造进行介绍：UOV体制、STS体制、MI体制、HFE体制、MFE体制和l-IC体制，以及 PQC′2013上新提出的 Simple Matrix方案。

3.1 MI体制

MI体制是由Matsumoto和Imai提出的最早的多变量密码方案，其主要理念是：以基域及其扩域构造了一个多变量陷门。

设有限域 F=GF（q），E是 F的 n次扩域，π：E→Fn是扩域E到向量空间的同构映射，正整数λ∈N满足 gcd（qn-1，qλ+1）=1，则称中心映射为如下形式的为 MI体制：

在此，条件 gcd（qn-1，qλ+1）=1可保证 Q 是一个可逆函数。

最原始的MI加密方案虽然已被攻破，但是其变型版本如Flash签名体制[34]和 PMI+[13]较为可靠。加密体制仍然是值得研究和探索的，并且在实用领域，Flash签名被NEESSIE计划所采用，被应用于低端智能卡；而后Ding等人结合内部扰动方法，对MI体制做了改进，提出了 PMI+体制，到目前为止，并未出现一种针对此方案的有效攻击算法。

3.2 HFE体制

隐域方程体制（Hidden Field Equations，HFE）是对MI体制（C*加密方案）的推广，由 Patarin提出[6]，其核心映射建立在扩域上，由单变量多项式构成，区别于MI体制核心映射的单变量单项式。

仍设有限域F=GF（q），E是F的n次扩域，π：E→Fn是扩域E到向量空间Fn的同构映射，HFE体制的中心映射具有如下的形式：

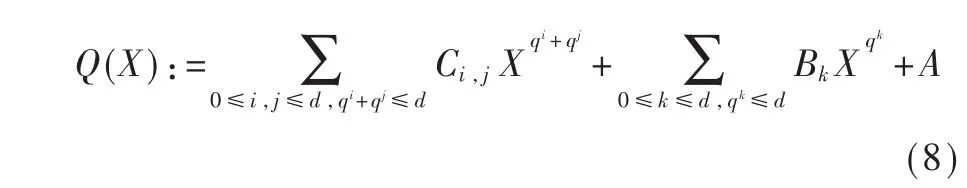
其中 i，j∈N， 次数 d∈N，Ci，j∈E 表示上式中二次项的系数，Bk∈E则代表其中一次项的系数，A∈E是常数项。

对于核心映射Q的求逆，需要利用Berlekamp算法（所有的运算都在有限域上进行），其计算复杂度为O（nd2logd+d3），因此，参数 d的取值不能太大。

HFE密码体制的主要变型有两种：一是Quartz签名体制[15]，一是 IPHFE[14]加密体制。HFE相关系统多年来受到了很多关注和各种密码分析，2013年，Ding等人对HFEv-签名方案的代数密码分析的复杂性提出了第一个稳定的理论估计。针对Kipnis-Shamir（KS）攻击的minors建模方法对于 HFE非常有效，但是当移除的方程数大于1时，导致失败。2017年，Vates等人依然基于minors建模方法推出一个新的适用于HFE-的所有参数的密钥恢复攻击方法。2014年Porras等人提出了ZHFE方案，公钥的核心映射是两个高阶HFE多项式构造的。2016年，Baena等人对ZHFE进行改进，提出新的算法使得ZHFE生成密钥的速度得到很大提升。但在2017年，Cabarcas等人发现利用ZHFE的低秩性质可对其进行密钥恢复攻击。同年，Petzoldt、Ding等人提出了一个有效的多变量签名HMFEv-，可以看作是Gui和Quartz的扩展版本，可抵御直接攻击与Rank攻击。

3.3 UOV体制

不平衡油醋密码体制（Unbalanced Oil and Vinegar，UOV）是对平衡油醋体制（Oil and Vivegar，OV）的改进。1998年，Kipins和Shamir利用二次多项式定义的二次型相关的矩阵方法成功地攻击了OV体制，伪造出了油醋体制的合法密钥；在此基础上，他们于1999年提出了不平衡油醋（UOV）体制。著名彩虹体制就是一种变形的油醋体制（即多层油醋体制[21]），多层油醋体制中的每一层都是油醋多项式，上一层中的所有变量都是下一层的醋变量。2013年，Petzoldt，Bulygin等人提出了一种运用Large Factor来缩短UOV和Rainbow签名方案的公钥方法，并实现了快速验证。2017年，Ding等人在FPGA上完成对 Rainbow Signature的高速硬件实现。

油醋体制的中心映射是建立在基域之上，其结构为：设有限域 F=GF（q），UOV的中心映射

在这里，x1，…，xo被称为油变量“Oil”，x~1，…，x~n-o则称为醋变量“Vinegar”。在此中心映射中，二次项是由醋变量与醋变量运算产生的，而与油变量相关的二次项只与醋变量结合产生，因此，当醋变量的值给定后，上面的多项式方程组就成了关于油变量的线性方程组，可以根据高斯消元法很容易地得到方程组的解。

3.4 STS体制

三角阶梯体制（Step-Wise Triangular Systems，STS）首先由Moh提出，其安全性可归约到复合的非线性的可逆多项式映射分解的困难性上。将STS体制的中心映射定义为Q，其基本架构介绍如下：

在上面的结构当中，1≤l≤L，l表示步数；nl表示在每步中增加的新变量的数量（步宽）；ml表示在每步中方程的数量（步高）。若以m和n分别表示方程的数目和自变量的数目，则一定存在关系n1+…+nL=n，m1+…+mL=m。

当每一步的步宽和步长相同时n1=…=nL=m1=…=mL，称此结构为正则 STS，公式（10）描述的就是正则STS的结构。

3.5 MFE体制

中间域（Medium-Field Extension Scheme，MFE）体制于2006年提出，由于核心映射中（有限域）域的扩张并没有包含所有的变量，因此被称之为“中间域”。MFE的核心映射采用了一种特殊的矩阵构造，将明文与密文之间的对应关系由这个矩阵来定义，由此构造了一个与MI体制和HFE体制等不同的核心映射（即不采用单个的多项式的形式）。

与前述的多变量密码体制相比，MFE具有如下明显特点：（1）因为采用了中间域的思想，使得域的扩张次数减少，大大缩短了公钥的长度，降低了计算复杂度；（2）MFE体制的核心映射采用了与Tame映射类似的形式，提高了密钥生成的效率，从另一方面提高了方案的效率；（3）因MFE体制的核心映射与具有特殊构造的矩阵存在对应关系，使得破解方案的困难性加大，难以用常规的攻击方法来破解此算法（从另一个角度促进了密码分析方法的研究）。由Ding等人所提出的SOLE攻击就是一种针对MFE体制有效的攻击方式。

3.6 Simple Matrix方案

Simple Matrix（ABC）方案是在 2013年[20]由 Ding等人提出来的新的多变量加密方案。这是一种基于矩阵乘法的简单高效的多变量公钥加密方案，该方案没有低秩的性质。具体一点是指与中心映射相关的二次方程的形式不具有低秩的性质，而其秩是与某个特定的参数n有关，进而可以加强对MinRank攻击的防御。ABC方案的另一个亮点是解密计算速度非常快，因为主要计算是解决某些线性方程。2014年，Ding等人对 Simple Matrix（ABC）方案进行了改进，提出了Cubic Simple Matrix加密方案[25]，使得安全性更高。通过利用具有随机二次多项式的方阵，使得用代数攻击破坏系统至少和求解一组随机二次方程一样难。此外，由于在矩阵中使用随机多项式，与中心映射关联的矩阵具有高秩，这防止了Rank攻击，得到的公钥是一个三次映射。

2014年，Smith-Tone等人根据ABC方案核心映射所固有的差分不变量提出了结构性的密钥恢复攻击，在对原始方案及其推广方案的攻击方法中渐近最优。2017年，Smith-Tone等人又对特征参数为2的Cubic ABC Simple Matrix加密方案的攻击方法进行了改进。

4 针对多变量密码的攻击方法

除强力搜索攻击外，针对多变量密码体制的分析方法主要有：线性化方程、XL算法、Gröbner基算法、秩攻击及差分攻击等。

4.1 解非线性化方程方法

XL算法和 Gröbner基算法是主要的解非线性化方程的方法。

在多变量公钥密码系统当中，将密文变量代入公钥多项式，可以得到一组关于明文变量的多项式方程组Y=F（X），直接的想法就是解此非线性方程组，从而得到明文。XL算法的本质是计算 Gröbner基，可以看作是算法的一种冗余变体，目前最有效的求 Gröbner基的方法是由 Faugere所提出的 F4和F5算法，利用F5算法，可以破解针对HFE体制的挑战 1。文献[35]中指出，F5算法通过计算Gröbner基的方法破解多变量密码算法的计算复杂度约为20.873n，其中 n为变量的数目。

4.2 线性化方程方法

线性化方程的攻击方法最初是用来攻击MI体制的，由Patarin[6]提出。线性化方程方法的原理是，在多变量密码方案中，若密文变量yi和相应的明文变量xi之间（首先要保证明文与密文的合法性）存在如下关系：

则称此方案满足线性化方程。

线性化方程攻击方法的优势在于得到的线性化方程与密文无关，只要公钥信息是已知的，则该过程就可以执行，此方法的特点在于：若要攻击已知其公钥信息的密码方案，则其所有的线性化方程都可以预先进行计算。

4.3 秩攻击

秩攻击是结合多变量公钥密码方案核心映射构造的特点，通过将公钥多项式的系数表示成矩阵的形式，从矩阵的秩的角度或矩阵奇异性的角度对多变量密码方案进行私钥恢复攻击。现有秩攻击有三种：

（1）油醋分离攻击：这一种攻击方法主要用来分析油醋（OV）体制和不平衡油醋（UOV）体制以及油醋方案的变体方案，如彩虹体制、多层油醋签名等，其计算复杂度为：q2v-n-1（n-v）4，其中 v为醋变量的个数，而n则为变量数。

（2）低秩攻击（小秩攻击）：这一类攻击最初提出是用来攻击隐域方程体制（HFE）的。

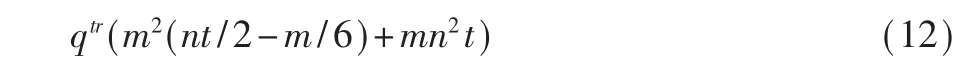
（3）高秩攻击[27]：此类攻击最初提出是用来攻击基于双有理转换的签名体制（此签名体制由Shamir提出）的。文献[27]指出，高秩攻击在攻击多变量密码体制时的计算复杂度约为qu（un2+n3/6），其中u代表在核心映射多项式中出现最少的变量所出现的次数，n表示核心映射中变量的数目。

4.4 差分攻击

差分攻击最初由Fouque[29]等人提出，用以分析加密体制，其原理是：通过将计算核心映射的双线性差分和线性化方程攻击的方法相结合来恢复明文。

中心映射F（函数）所对应的差分（算子）定义为：

此形式为域上的一个双线性函数。

2008年，Fouque[36]等人成功地利用差分攻击的方法攻破了l-IC方案。Billet等人于2009年将针对多变量公钥密码体制的差分攻击方法作了改进，并利用改进后的差分攻击方法攻击了Square-Vinegar签名方案和 Square加密方案[37]，分别得到了合法的伪造密文和正确的明文。2011年，Smith-Tone提出线性映射空间的大小可以作为决定差分安全的一个度量，空间越大越不安全。2013年，Perlner和Smith-Tone指出可以通过对差分不变量进行分类来抵抗差分攻击。通过指出域映射中所有可能的线性差分不变量，就可以指出线性系统中可能会被攻击者利用到的差分，从而确保系统可以抵抗对应的攻击模型。2014年，Daniels同样和 Smith-Tone，对HFE和HFE-的核心映射进行研究，推导出差分对称性与结构不变量，并提供了一组参数的集合使得HFE体制对差分攻击的安全性得到提高。2016年，Cartor和Smith-Tone等人对HFEv Signature Primitive的差分安全性进行了分析，并提出了新的可以抵抗差分攻击的方案。

差分攻击的优点就在于其可以降低其所要攻击函数的次数，这样就大大减少了攻击的计算复杂度，在寻找私钥当中特殊的线性关系方面有着巨大的优势。随着对差分攻击研究的深入，其在多变量公钥密码体制分析方面正在发挥越来越重要的作用，在密码方案的构造及改进的过程中要将此攻击方法作为一种重要的攻击类型来对待。

5 结论

多变量公钥密码系统的研究仍然存在许多不足，有很多相关的工作要完善，具体来说有以下三个方面：

（1）多变量公钥密码方案设计的基础是数学理论，图论、矩阵论等代数或几何概念为方案的陷门构造提供了新思路，推动了各种新方案的提出。另外，通过对攻击方法的深入研究，分析旧方案，也能够设计出新的多变量公钥密码方案。因此，数学理论、结构的研究以及旧方案的分析改进将来一定能在构造新多变量公钥密码系统上发挥作用。

（2）在多变量公钥密码系统的实际应用上，存在公钥长度过大的不足。如何针对资源和计算能力受限的小型设备，设计密钥量较小的多变量公钥密码方案也是另一个吸引人的方向。

（3）对于多变量公钥密码系统的密码分析和形式化证明的研究。方案设计伴随着方案攻击，新型攻击方法的研究仍然是研究重点。另外，对多变量公钥密码安全性的形式化证明也应该是安全性研究中的一个重要方面。