基于RLWE的可撤销分层属性加密方案*

郭凯阳 ，韩 益 亮 ，吴日铭

（1.武警工程大学 密码工程学院，陕西 西安 710086；2.武警部队密码与信息安全保密重点实验室，陕西 西安710086）

0 引言

在信息时代与大数据时代的背景下，当今网络中的信息量呈现爆炸式的增长，网络信息安全问题引起了人们的广泛关注，密码技术作为保障信息安全的关键技术之一，其研究发展也越来越受到重视。1976年Diffle和Hellman提出了公钥密码思想体制[1]，解决了对称密码体制中密钥管理代价高、功能单一等问题，但是随着需求发展，传统基于公钥基础设施的加密机制也遇到了一些瓶颈，为了提高效率，Shamir于1984年提出了基于身份的加密机制（Identity-Based Encryption，IBE）[2]，在此基础上，Sahai和 Waters进一步提出了属性加密机制[3]。属性加密机制实现了一对多的加密模式且具有灵活的访问结构，通常分为密文策略属性加密（Ciphertext-Policy Attribute Based Encryption，CP-ABE）和密钥策略属性加密（Key-Policy Attribute Based Encryption，KP-ABE）[4]。为了完善属性加密机制的功能，发掘其潜在的应用前景，田有亮等人提出了基于属性加密的区块链数据溯源算法[5]；刘建华等人在属性加密的基础上提出了支持密文检索的云存储方案[6]；王峥等人提出了雾计算中用户和属性可撤销的访问控制方案[7]；汪金苗等人基于多授权的属性加密设计了面向区块链的隐私保护和访问控制方案[8]。

构造简单、抗量子攻击是格密码体制的两大优点，Regev在2005年提出了格上的误差学习问题（Learning With Error，LWE）[9]，并指出可以用来设计身份加密和属性加密方案，之后构造格上的属性加密方案成为了学者研究的热点之一，张欣等人利用二叉树设计了可撤销属性的格基属性加密方案[10]。Tan等人利用LSSS技术构造了理想格上的高效CP-ABE方案[11]。吴立强等人提出了一种基于RLWE问题的高效模糊身份的加密方案[12]。于金霞等人提出了一种基于RLWE的支持访问树的属性加密方案[13]，之后基于LWE问题设计了一个外包环境下可撤销的属性基加密方案[14]。

在大多数属性加密方案中，通常都是将所有的属性归在同一个层次，无法根据属性之间的层次关系实现灵活高效的访问控制。因此在2009年，Jin Li等人提出了将属性分层处理的加密思想[15]，并通过构建不同类的属性树设计了一个分层的属性加密方案（Hierarchy Attribute-Based Encryption，HABE）。2014年Liu等人通过将属性分布在不同的矩阵行中也实现了属性分层[16]。2016年王梓莹等人在其方案中给出了一个新的属性分层加密的形式化定义[17]。目前分层属性加密方案的构造大多是基于双线性对映射且不具备其他功能，基于格基来构造分层属性加密方案的例子较少。

为了使方案更加满足实际需要，本文在Tan[11]等人的CP-ABE方案的基础上对其进行改进，在研究格上属性加密方案的同时尝试将属性进行分层，并参考王光波等人方案中的撤销思想[18]，设计了一种基于RLWE的支持撤销的分层属性加密方案。方案采用第三方机构进行撤销减少了系统的工作量，采用改进的分层访问结构可以实现灵活的访问策略，在兼具抗量子攻击的同时实现了属性分层及即时撤销。

1 预备知识

1.1 困难问题

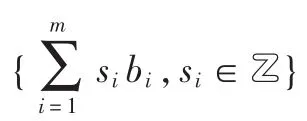
定义 3理想格 如果存在一个环 R=[x]/＜f＞和一个理想 I⊆R且格 Λ∈Zn与 I相关，则称其为理想格。

定义4判定型环上误差学习问题 给定安全参数 λ，选 d、q为基于 λ 的整数，定义 R=Z[x]/f（x）是模 f（x）的整数多项式环，Rq=Z[x]/f（x）表示模 f（x）和q的整数多项式环，其中，f（x）=xn+1。给定基于 λ的离散分布 χ⊂Rq，判定性 RLWE问题中有一个指定的挑战模型 O，对于 s∈Rq，判定该挑战模型是含有噪声的伪随机采样机Os还是真正的随机采样机，其中Os和有以下特征。

Os：输出伪随机 样本，即（ω，v）=（ω，ωs+e）∈Rq×Rq，且样本中含有噪声，其中，ω为环多项式，s∈Rq表示均匀分布的密钥，e是系数取自离散分布χ的噪声。

1.2 分层门限秘密共享方案

Tamir在2007年提出了分层门限秘密共享方案[19]，其原理与LSSS方案相似，都是通过满足访问结构的参与者重构多项式进而恢复出秘密，不同的是方案中运用求导的方法来区分参与者之间的层次，高等级对应较低层，子秘密中包含的秘密信息多，低等级则正好相反。在此基础上，毛颖颖等人提出用一个自定义函数运算代替求导进而提高了原方案的运算效率[20]，本文在构造访问结构时使用的就是毛颖颖改进的分层门限秘密共享方案，下面对此方案进行介绍。

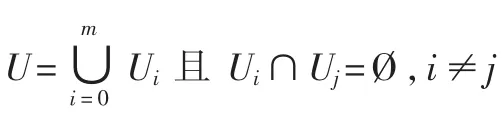
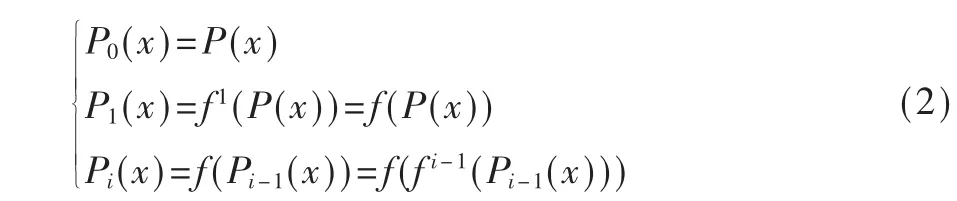
在恢复秘密时，V={v1，v2，…，v|v|}⊂U 表示授权属性的集合，满足：

…

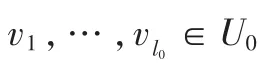
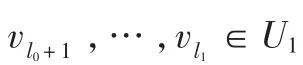
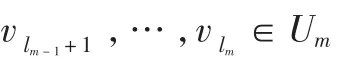
其中 0≤l0≤l1≤…≤lm=|V|，当且仅当对于所有的 0≤i≤m，li≥ki， 则 V作为一个授权子集， 列出方 程 Fv·（→）T=σT， 即 ：

则通过计算可以恢复出秘密s。

1.3 安全模型

定义了一个选择明文攻击下的不可区分性游戏模型，游戏包括一个模拟器和一个敌手，具体定义如下：

阶段 2：重复阶段 1。

猜测：敌手提交对 b的猜想 b′。

2 方案设计

方案中系统根据属性的重要程度将不同的属性划分为不同的等级，每个用户持有一组属性的私钥，当数据拥有者在设置访问策略时，可以依据属性的级别不同设置更为细粒度的控制策略，只有当数据访问者的属性集中，每层属性的个数超过访问策略中设定的每层属性的个数的门限值时，才能成功通过密钥解密密文，且一般高等级属性的门限值要小于低等级属性的门限值，在解密过程中，高等级属性的解密能力要大于低等级属性的解密能力，且可以避免高等级的属性被多个低等级属性合作取代的情况出现。

2.1 形式化描述

方案构架如图1所示，本文方案主要包括5个主体部分：

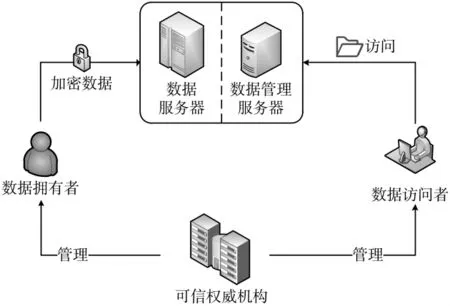
图1 方案架构

可信权威机构：生成系统的公共参数和主私钥，为每个合法的用户构造私钥并负责属性的更新与撤销。

数据管理服务器：管理上传到服务器中的数据，实现外部用户的访问控制。

数据服务器：存储上传到服务器中的数据。

数据拥有者：设置此密文的访问策略对数据进行加密，并将其上传到数据服务器。

数据访问者：对数据服务器上的数据进行访问。

本文方案共分为6个部分：（1）可信权威机构生成公共参数和主密钥；（2）为注册的用户生成私钥；（3）已经注册的用户根据自己设置的访问策略加密需要共享的数据并将其上传至服务器中；（4）当服务器中的数据中涉及到属性撤销时，生成数据加密密钥；（5）是对数据重加密；（6）数据访问者利用自己的私钥对数据进行解密，具体流程如图2所示。

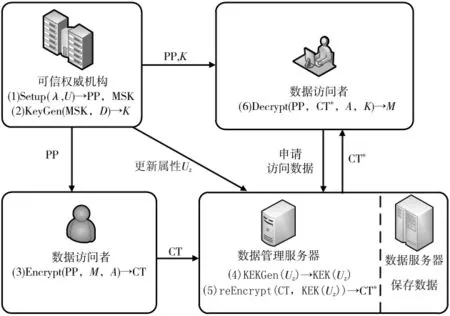
图2 方案流程图

Encrypt（PP，M，A）→CT：该算法由加密者执行，输入公共参数PP，明文消息M和一个属性集U上的访问结构 A，输出密文 CT。

KeyGen（MSK，D）→K：该算法由授权机构执行，输入主密钥MSK和一个用户属性集合D，为用户输出一个私钥K。

KEKGen（Uz）→KEK（Uz）：该算法由数据管理服务器执行，若属性Z中用户信息更新，输入属性Z更新后的属性用户群Uz，为更新后的用户群中的每个合法用户输出密钥加密密钥KEK（Uz）。

reEncrypt（CT，KEK（Uz））→CT*：该算法由数据管理服务器执行，输入密文CT和密钥加密密钥KEK（Uz），对密文进行重加密，输出CT*。

Decrypt（PP，CT*，A，K）→M：该算法由用户执行，输入公共参数 PP，用户的密钥 K，重加密密文CT*，根据属性更新后该用户是否仍然满足访问结构A对密文进行解密，解密成功输出M，否则输出⊥。

2.2 具体构造

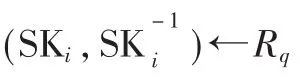
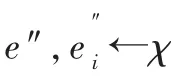
（1）色谱条件：XBridgeTM-C18色谱柱（250 mm×4.6 mm，5 μm）；填充剂为十八烷基硅烷键合硅胶；流动相为乙腈-0.5%氨水，梯度洗脱：0～45 min，30%～60%乙腈；45～80 min，60%～80%乙腈；体积流量0.5 mL/min；检测波长235 nm；柱温30 ℃；进样量20 μL。理论板数按乌头碱计算不低于6 500。

密钥加密密钥生成 KEKGen（Uz）：数据管理服务器收到关于属性z的更新属性群Uz后，输出KEK（Uz），建立过程为：

将属性群中的每个成员都分布到一棵完全二叉树的叶子节点上，令每个节点vz对应一个随机密钥KEKz，如图3所示。若 ut∈U为树中的某叶子节点，令KLt为ut到根节点所对应的所有随机密钥的集合。例如，图3中u3的随机密钥链集合KL3={KEK10，KEK5，KEK2，KEK1}， 对 于 属 性 用 户 群 Uz，KEK（Uz）表示二叉树与Uz中用户对应随机密钥的最小覆盖集。 例如，假设 Uz={u1，u2，u5，u6，u7，u8}，则在图 3 中KEK（Uz）={KEK3，KEK4}。

图3 属性用户群构造的二叉树

数据重 加 密 reEncrypt（CT，KEK（Uz））：数据 管 理服务器收到加密密文后，根据属性更新情况，对密文进行再次加密。

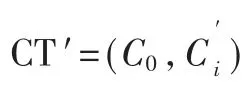
（2）生成头文件信息 Hdr={Ek（f-1）}k∈KEK（Uz），其中Ek（f-1）表示以k为密钥的快速对称加密。

当用户申请访问数据时，将重加密密文CT*=（Hdr，CT′）发送给用户。

数据解密 Decrypt（PP，CT*，A，K）：输 入公共参数 PP，用户的密钥 K，重加密密文（Hdr，CT′）。

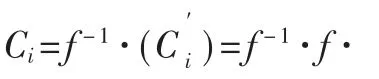
3 方案分析

3.1 正确性分析

若通过方案的解密部分正确解密密文，则验证方案算法正确，下面对解密部分进行计算：

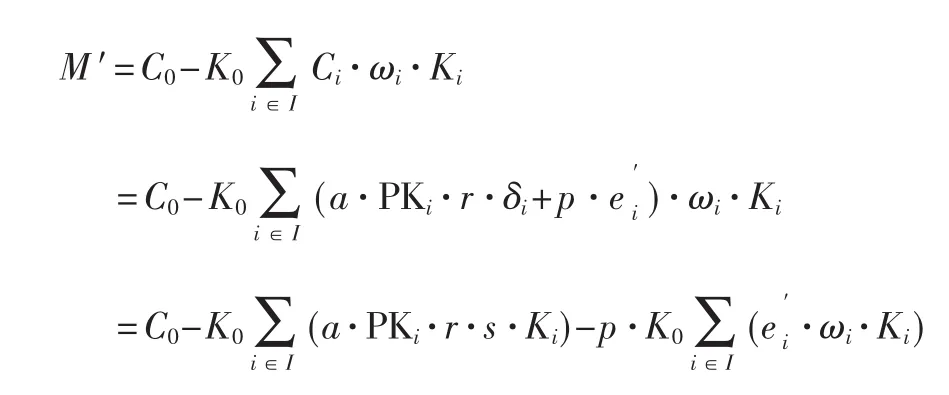
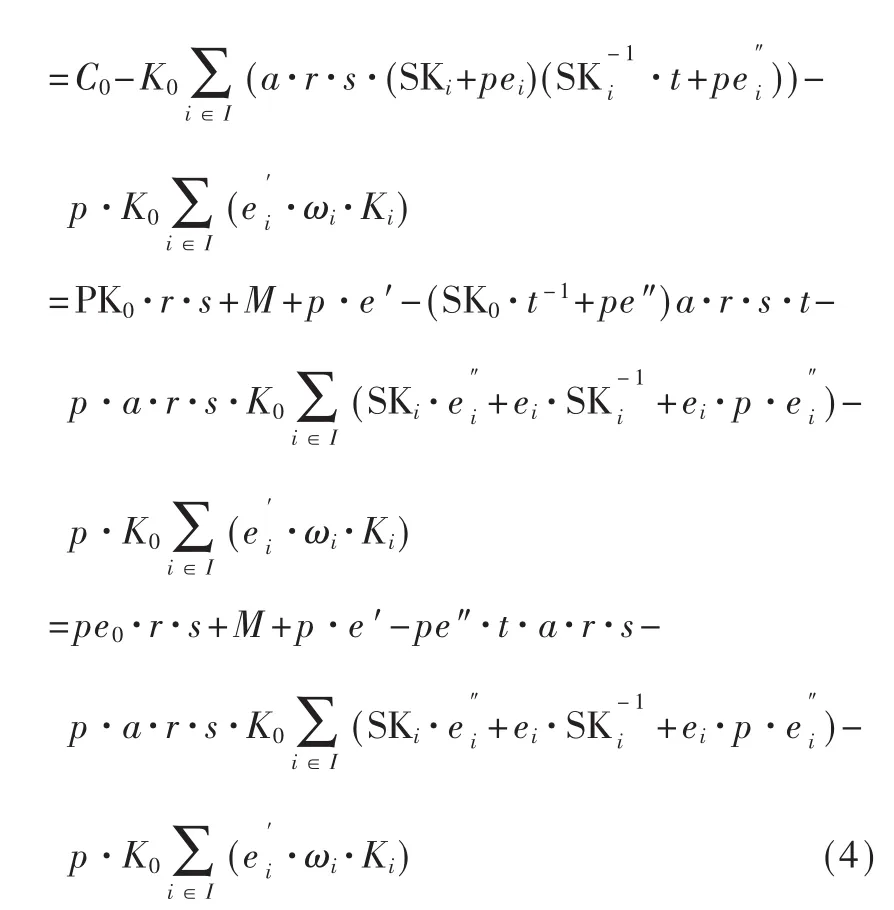
进一步计算得出 M=M′mod p。

3.2 安全性分析

合谋攻击是属性加密中常见的攻击手段，系统中的恶意用户会将他们的属性集联合起来，对一些他们各自权限之外的密文进行非法解密。为了抵抗这种合谋攻击，本文方案在用户密钥生成过程中采用随机化处理的方法，在每个密钥中都嵌入一个随机元素t∈Rq，这是每个用户独有的进而使用户之间无法联合，增加了恶意用户合谋攻击的难度，下面重点证明方案的选择明文攻击下的不可区分性安全。

证明 判定型RLWE问题是针对挑战预言机O，对于 SK0∈Rq，判定该挑战模型是含有噪声的伪随机采样机Os还是真正的随机采样机。询问挑战 预 言 机 O（t+1）次 ， 并 返 回 （ωk，υk）∈Rq×Rq， 其 中k∈{0，1，2，…，t}，游戏按照以下步骤运行。

阶段1：查询密钥及密钥加密密钥。

阶段 2：重复阶段 1。

则B的优势为：

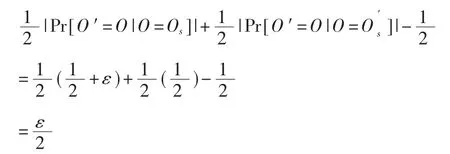
3.3 效率分析

本文方案基于格上RLWE问题构造了一个CP-ABE方案，选取一些其他的格上密文策略方案从访问结构、困难问题、私钥长度、密文长度以及是否支持属性撤销和分层等方面进行对比，具体结果如表1所示，其中Ac表示加密属性个数，Au表示用户属性规模，n、m为格上的相关参数。

表1 相关方案对比

从表1中可以看出，文献[10]仅仅支持门限访问结构，访问结构不够灵活，文献[13]和[14]采取访问树的访问结构，文献[11]采取LSSS访问结构，本文采取的是分层秘密共享访问结构，都可以实现与、或和门限操作。文献[10]和文献[14]基于LWE构造，私钥长度分别为 2mAulogq和 mAulogq，文献[11]和文献[13]及本文方案基于RLWE构造，文献[14]的私钥长度为 mAulog q，文献[11]、[13]和本文方案的私钥长度为（nAu+n）logq，因为参数之间存在m≥5nlogq的关系，所以本文方案的私钥长度小于文献[10]和文献[14]，同样在密文尺寸上，本文方案的密文长度小于文献[10]和文献[14]。文献[11]和文献[13]不支持属性撤销和属性分层，文献[10]和文献[14]虽然支持属性撤销，但不支持属性分层，本文方案在支持属性分层的同时也能实现属性撤销。

4 结论

本文利用格上的RLWE问题构造了支持属性分层的可撤销CP-ABE方案，并证明了满足抗合谋攻击和选择明文攻击下的安全性，方案采用多等级门限秘密共享访问控制矩阵实现了属性的分层，在云环境的基础上通过第三方机构控制用户对属性陷门的获取实现了高效的属性撤销，在功能和性能上更适用于实际应用环境。但是方案仅仅依靠第三方实现了属性的间接撤销，且并未考虑对隐私信息的保护和泄露密钥的追踪问题，如何实现用户或者属性的直接撤销，以及属性加密机制的隐私保护和叛逆者追踪问题将是之后研究的重点。