突变流道内空泡脱落特性及空蚀损伤分析

王江云王 壮侯琳倩王 娟解 凯

(1.中国石油大学(北京) 克拉玛依校区,新疆 克拉玛依 834000;2.中国石油大学(北京) 重质油国家重点实验室,北京 102249;3.过程流体过滤与分离技术北京市重点实验室,北京 102249;4.西安益翔航电科技有限公司,陕西西安 710065)

当流体流经通流件内突变流道时,会产生节流[1]、增速或获得升阻力[2]等现象,当流体局部压力低于其饱和蒸汽压时,就会发生空化,进而产生空蚀现象,造成通流件壁面损伤[3]。作为空蚀的先决条件[4],空化是一种涉及相变、多尺度湍流和非定常性等的复杂现象[5],严重影响着突变流道内流体流态的演变,造成部分通流件内流动失稳,影响正常工作生产[6-8]。

为了探究突变流道内空化流动的非定常特性及其发展演变的复杂多样性,诸多学者针对叶轮流道[9-10]、文丘里流道[11-13]、水翼流道[14-16]及头型钝体[17-18]等的空化初生、发展、流场变化特性、空泡演变及脱落机理等做了较为详细的分析;Li等[19]还发现了空化的发生、发展十分依赖流道的结构,空化初生依附位置甚至决定了整个流场的变化。然而,上述分析大多基于成熟发展的流道结构,且偏向于对空化现象本身所引起的流动特性研究,而针对较为复杂的突变流道内空化的发生、发展与流道自身结构耦合作用的研究还较少,对其内空泡的非定常脱落特性、整个演化过程的准周期特性和由空化造成的空蚀效应的综合研究还不够清晰,对空蚀损伤的定量预测还不够准确。

因此,笔者针对Krella[20]设计的空化室进行数值模拟分析,探究流道自身结构约束下空泡脱落的演变规律,量化空化条件下壁面剪切力的程度,分析空蚀损伤规律,以期从复杂流道结构的耦合影响方面为空化的发展特性和空蚀效应的定量分析提供理论基础。

1 空化模型与计算方法

1.1 实验装置

为研究空化室内空泡行为,参照Krella设计的空化室进行实验装置的搭建。图1为实验装置示意图,主要包括空化室、贮水罐、泵、电磁流量计、电动闸阀等。实验装置的压力调节范围为0.1～1.0 MPa,流体流量测量范围为0～50 m3/h。实验中可以通过调节流体流量和管道狭缝开度,使空化室喉部节流降压,产生不同类型的空化,进行空化强弱的改变。

图1 空化空蚀实验装置示意图Fig.1 Diagram of cavitation test device

1.2 空化室结构及网格划分

图2为高度30 mm方腔空化室二维结构示意图[20]及其监测区域和计算网格划分。空化室内设有半径均为9 mm的上、下2个圆形凸台,可移动下凸台以改变节流缝宽(图2(a))。在此研究中,节流缝宽取为3 mm。由于研究重点考察空泡的产生、发展、逐渐脱落的过程,因而主要涉及流体流动的主流方向;同时空化室三维结构在展向上的尺寸远大于狭缝尺寸,使展向流动对主流方向上流体空化过程的影响可以忽略,因此采用二维模型计算分析。空蚀靶区内的监测区域均分为6个区域,编号1～6,如图2(b)所示。空化室计算网格的划分利用ICEM CFD软件进行(图2(c)),为保证湍流的充分发展和数值迭代计算的稳定性,将入口段延长为3倍当量直径,出口段延长为5倍当量直径。对两凸台位置处进行边界层设置和网格加密处理,越靠近凸台网格越密,网格数目约32万;最小网格厚度约10-5m,凸台近壁处第一层网格的无量纲距离y+≈2。

图2 空化室二维结构、监测区域及网格划分Fig.2 2D structure,monitoring areas and grid generation of cavitation chamber

1.3 数学模型选择

1.3.1 湍流模型

对流场分析过程中,为求解湍流细节而引入的不同模式的湍流理论称为湍流模型。不同湍流模型对流场考察方向和求解精度不同,雷诺时均模型是一种求解时均流场特性的湍流模型。在雷诺时均模型中,标准k-ε模型在数值计算过程中稳定性好,但求解精度稍差,且不适于捕捉流场内涡旋;重整化群(RNG)k-ε模型则对湍流黏度系数加以修正,增加了反映主流时均应变率的项,可以较好地处理旋流、流线弯曲程度较大的流动,但其基于各项同性的涡黏性假设使其对强旋流问题的描述仍有不足;雷诺应力模型(RSM)严格考虑了流线弯曲、旋转和张力快速变化等因素,同时避免了各向同性的涡黏性假设,因而考虑的物理学机制更加全面,对于复杂流道结构内突扩、突缩流动分离区和湍流各向异性较强的流动具有很好的模拟能力,能反映出涡旋流场的基本特征[21-22]。因此,笔者选用RSM模型捕捉空化室内湍流发展区的涡旋。

1.3.2 多相流模型

空化室内空化现象的发展演变过程非常复杂。空化流动是一种掺杂气、液两相的混合流动;在空泡群充分发展区内,气、液两相互相穿插,且二者在混合流动中存在速度差异,随主流运动时存在速度滑移[23]。在多相流模型中,Mixture模型适用于含空泡的混合流,可以实现对空泡群的捕捉和空泡均匀度的刻画,被广泛应用于对空化问题的研究中[5,16,24]。

1.3.3 壁面函数

空化初生严格依赖壁面结构,且通常发生在流动剪切层内[25]。为了较好地捕捉流体转捩点和分离转捩区,模拟计算时就要求空化初生特征位置处的近壁法向网格足够密。增强壁面函数[26]不依赖于壁面法则,结合了壁面分布律在黏性底层内的线性关系与黏性底层外的对数关系,y+通常在1数量级范围内,适用于近壁处空化初生及空泡脱落分离的模拟刻画。

1.3.4 空化模型

空化模型的选用对空化问题的研究尤为重要,已成熟发展应用的空化模型主要有ZGB(Zwart-Gerber-Belamri)模型[27]和SS(Schneer-Sauer)模型[28]。这2种空化模型都是基于空泡动力学Rayleigh-Plesset方程推导而来,相比较其他空化模型,二者在计算过程中具有更好的鲁棒性,能观察到明显的空泡运动。其中,ZGB模型假定所有空泡尺寸相同,相间的质量输运率和单个空泡的质量变化率由空泡密度所决定,对蒸发项考虑水中气核密度的影响;SS模型将空泡密度与蒸汽相体积分数关联起来求解输运方程,没有考虑不可凝结气体对空化流动的影响,而是将蒸汽相纳入到空泡密度中[29]。笔者分别采用2种空化模型进行模拟计算,并与实验结果进行对比。

1.4 计算条件

由于空化过程中流场内存在显著的压力波动,流场的非定常特性很明显,为捕捉空泡的演化行为、提高数值迭代运算的稳定性,采用非稳态求解器。参照CFL(Courant&Friedrichs&Lewy)计算收敛准则(式(1))[30],确定非稳态求解的时间步长为10-5s。计算过程中,设置液相为水;25℃时,其密度为999.19 kg/m3,动力黏度为0.001139 Pa·s,气相为理想状态水蒸气。边界条件设置为压力入口,压力出口,无滑移固体壁面。离散项采用控制容积积分法,压力差分格式为PRESTO格式,动量、体积分数、湍动能、湍流耗散率都采用高阶QUICK格式。湍流强度设置为0.5%,气相体积分数初始值为0,饱和蒸汽压设置为3169 Pa[31]。

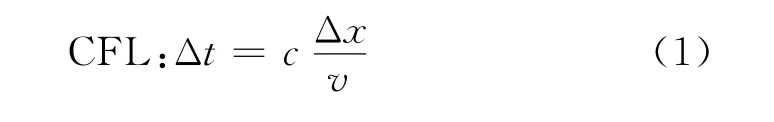
式(1)中:Δt为瞬态计算时间步长,s;Δx为网格尺寸,m;v为混合流体速度,m/s;c为库朗数,用于在计算时控制时间步长,笔者采用的隐式算法中取为40。

1.5 模型验证

采用RSM湍流模型、Mixture多相流模型、增强壁面函数,分别耦合ZGB空化模型和SS空化模型模拟计算得到空化室内液相的汽化体积分率(气体体积分数)云图,如图3(a)所示。对比图3(a)中(1)和(2),发现2种空化模型计算结果相似,在上、下凸台后缘均形成空化区域,但ZGB模型模拟结果(1)在上凸台边缘出现明显的空泡黏附和脱落现象,与实验拍摄(图3(b))的空化室内空泡产生位置及分布情况相吻合,说明采用RSM湍流模型、Mixture多相流模型、增强壁面函数和ZGB空化模型的模拟方法精度更高,可以用于空化室内脉动信息以及靶区壁面剪切力的分析。

图3 空化室内液相汽化体积分率(气体体积分数)Fig.3 Vaporization volume fraction in the cavitation chamber

2 二维空化室非定常流动特性分析

2.1 压力场与速度场分布

图4为空化室内不同进出口压差下的压力和流体速度分布云图。由图4(a)可知:在空化室内上凸台的后缘出现局部高压区,随着进出口压差的增大,高压区范围增大、中心压力值变大,但中心位置基本不变;同时,狭缝上下游压差也明显增大;沿流体流动方向,随着流道的逐渐扩张,下游处压力逐渐趋于稳定。由图4(b)可见,在流动过程中,狭缝喉部位置处流体速度出现明显的分层,下游越靠近下凸台,流体流速越低,流速最大区域对应狭缝来流,并在流场内形成主流区。上凸台后缘处存在明显的低速区,随着压差增大,低速区变得明显,且狭缝处流速增大。此外,对比发现,在3种压差下,压力和速度分布基本相似,由于狭缝处的节流作用使得狭缝处压力骤降,速度急剧增大。

图5为不同进出口压差下空化室内流体流线图和湍动能分布云图。由图5(a)可见:随着流道通流面积变小,靠近狭缝,流体流线逐渐收缩变得紧密,并沿凸台表面发生偏转;在位于上游凸台前端的折角处产生两处涡旋回流区,但区域较小;在下游凸台后端产生3处涡旋区(Ⅰ、Ⅱ、Ⅲ),且不同进出口压差下涡旋中心位置基本保持一致。随压差增大,Ⅰ区域涡旋范围逐渐扩大,与图4中压力和速度分布相对应;Ⅲ区域涡旋范围也逐渐扩大,且其涡旋中心有向下游移动的趋势;Ⅱ区域涡旋范围则逐渐变小。由图5(b)可知,上凸台后缘有明显的湍动区,且湍动区有明显的压力波动。此外,随着进出口压差增大,除狭缝迎流处,流场内湍动加剧,并逐渐占据主流场空间。

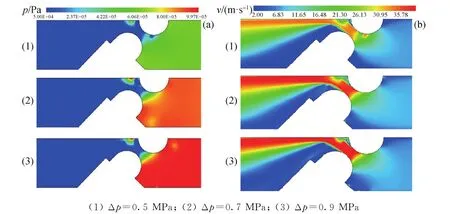
图4 不同进出口压差下空化室内压力和速度分布Fig.4 Pressure and velocity distribution in the cavitation chamber under different inlet and outlet pressure differences

图5 不同压差下空化室内流体流线和湍动能分布Fig.5 Streamline and turbulent kinetic energy distribution in the cavitation chamber under different pressure differences

综合分析,3处涡旋区域是空化室内流体重要的流动特征,且Ⅰ区域涡旋会受到附加的空化影响,空泡排开液体或空泡溃灭释放压力都会导致涡旋处湍动明显。

2.2 空化过程分析

空化现象具有显著的非定常特性。为便于研究空泡的演化特性,调节进口压力为0.46 MPa,出口压力为0.1 MPa,使得空化室内呈现出泡状空化状态。模拟发现,空泡演化呈准周期性的初生、发展、分离、脱落、溃灭过程,并分别以上、下凸台为空化初生依附位置,如图6中点f1、f2所示。受流道结构制约,该压力下的泡状空化初生点位于两凸台圆心连线上,且空化初生点皆位于凸台的迎流位置,因该处流速最大,近壁压力最低,最易满足空化条件。

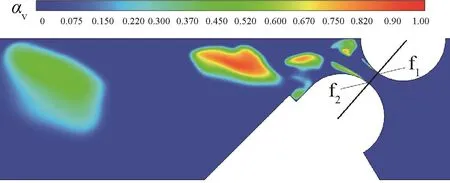
图6 空化初生依附点Fig.6 Cavitation primary attachment point

图7为空化室上、下凸台液相汽化体积分数监测结果。由图7可知,空泡发展的周期性明显,虽周期稍有差别,但演化规律基本一致,上凸台空泡的演化周期为0.057 s,下凸台的为0.059 s。

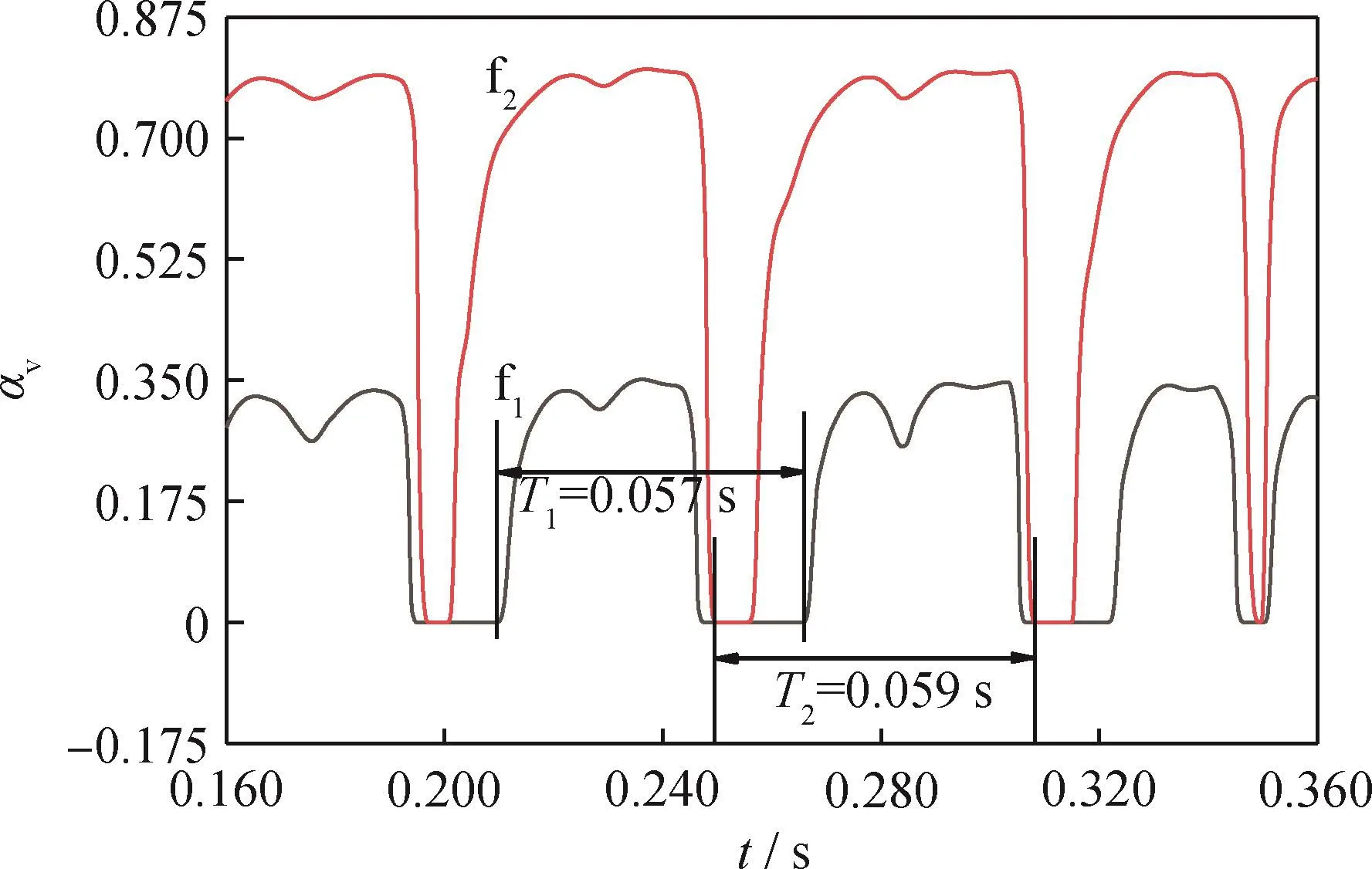
图7 空化室内液相汽化体积分率(气体体积分数)周期性变化曲线Fig.7 Periodic change curves of vaporization volume fraction in the cavitation chamber

图8演示了空化室一个周期内的空泡演变过程。在上凸台(图8(a)),沿着流动方向由(1)到(2),在空化初生处空泡初生、长大、脱落,体积不断增大;较大的空泡分离为小的空泡,并相互依附、黏连,逐渐发展至(3)中的大空泡而脱落分离;留下部分游离小泡,游离小泡会与脱落大空泡融合后体积变大,如(4)所示;继而向下游发展,生长至体积最大(见(5)),此时上凸台空化程度达到最强;自(5)开始,上凸台空化程度逐渐减弱,初生位置几乎不再给下游提供游离空泡,主体大空泡持续受压变小,一段时间后溃灭消失。而后在(8)时刻上凸台空化初生处重新初生空泡,重新开始下一周期的空泡演化,而整个周期约0.057 s。

在下凸台空化过程中(图8(b)),空泡演化的全过程约为0.059 s,其演化周期与上凸台的相近,演化过程与规律也相似;但相比于上凸台,下凸台的下游流场空间区域更大,能给空泡提供充足的演变空间和时间,空泡的演化行为也更加显著。而上凸台后缘则基本上一直处于高压涡旋区,流场区域范围小,抑制了空泡的初生和长大,会导致空泡出现非正常演化。在整个演化过程中,下凸台作为重要空化依附位置,液相的汽化体积分率要明显高于上凸台位置的。

图8 空泡演变过程Fig.8 Cavitation evolution process

2.3 空蚀损伤定量分析研究

空泡破裂时对壁面冲击的高剪切应力和速度会对壁面空蚀造成影响,将壁面定量损伤公式(式(2))用于量化分析空化损伤,并进行修正,取得了较好效果[4,32]。笔者采用自定义函数将损伤公式植入Ansys fluent软件内,来进行空蚀的定量分析。

式(2)中:Ecavitation为空蚀损伤率,mm/a;A为空蚀损伤实验常数,取值3.071×10-17[32];n为速度指数因子,与实验条件有关,取值6[4];τWSS为壁面剪切力,Pa。

上、下凸台空泡演化过程的周期性使空泡溃灭对壁面造成的剪切力冲击具有稳定的变化周期。不同位置处空泡或空泡群的演化行为不同、空泡数量不同、空化强度不同,则对应的损伤程度也不同,因此在靶区内的6个监测区域内分别计算壁面的损伤程度。6个区域内面加权平均的壁面剪切力结果如图9所示,其中图9(a)～(f)分别对应靶区1～6监测区内的壁面剪切力变化。由图9可知:壁面剪切力的周期性变化明显,不同区域的壁面剪切力变化周期和幅值不同,但二者基本呈现出负相关性;各区域内壁面剪切力的周期由小到大顺序为:T3、T4、T5、T6、T2、T1。

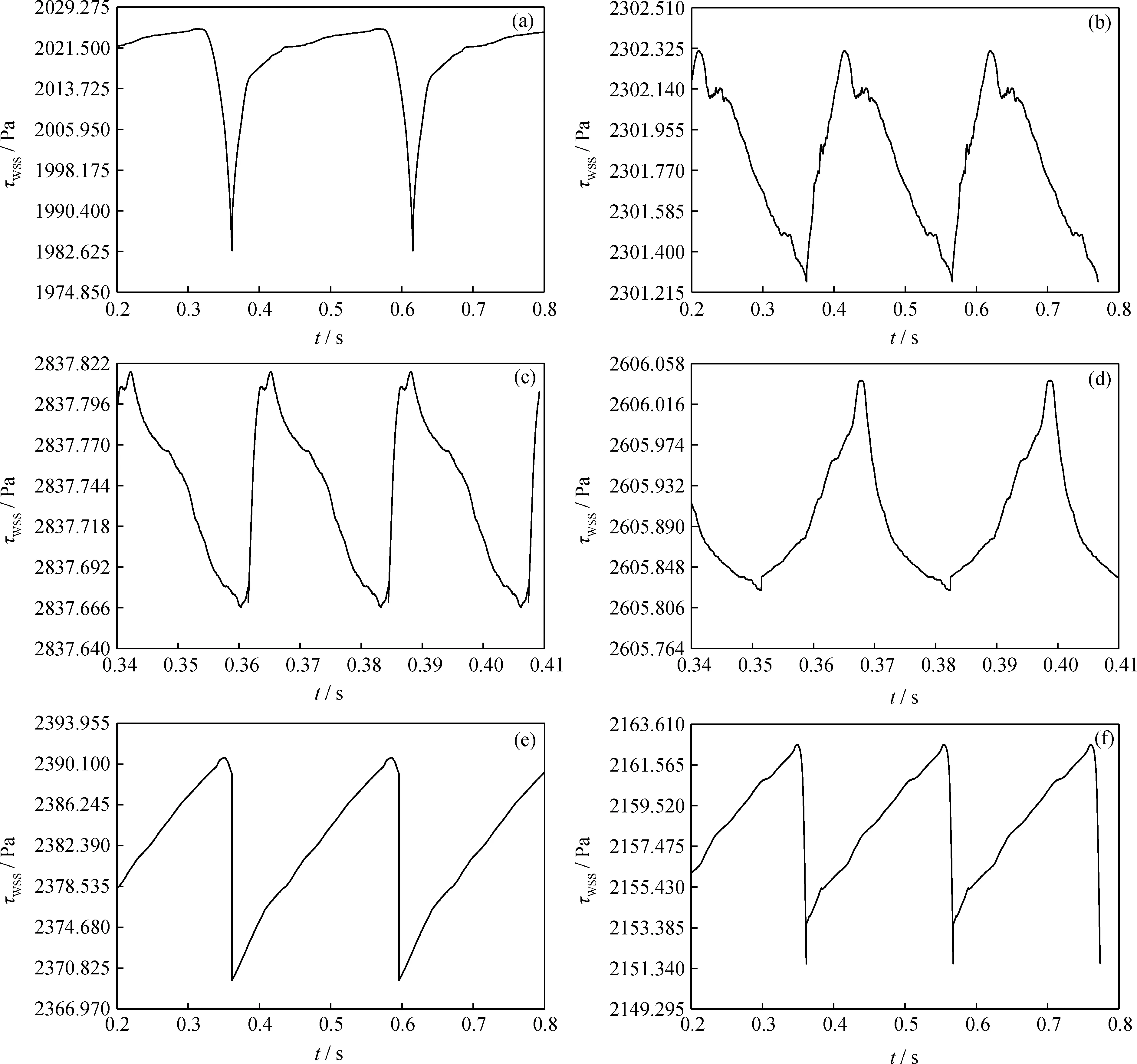
图9 靶区壁面剪切力变化曲线Fig.9 Shear force curves of the target wall

依据式(2)求得空蚀损伤速率的变化曲线如图10所示。由图10可知:沿着流体流动方向,靶区内空蚀速率先迅速增大,出现损伤量峰值后逐渐减小;最大损伤位置在区域3,其损伤速率最大。这是因为空蚀损伤主要是受到空泡群的破裂溃灭和流场冲击所致,而损伤速率在很大程度上又会受制于空泡的破裂行为;上凸台后缘空间较小,流体流速较低,大多数空泡发展没有经历充分的时间,达不到正常溃灭的条件;紧邻上凸台的区域1受到涡旋影响,多数空泡会被“挤走”排开,随狭缝主流移动到下游区域内,在区域3～6内发展溃灭,导致区域1并不会受到较大损伤,而区域3损伤最大。在区域2和3处损伤率有较大增速的主要原因是此处正对来流,来流会夹带部分空泡撞击壁面,造成较大的壁面剪切应力。

图10 靶区各区域内损伤程度Fig.10 Damage degree in each area of the target area

下凸台作为空化初生的主要依附位置,除了正对来流,下游发展空间充足,即使有涡旋的产生,也会促进该处空泡的发展演变。在图5(a)中,Ⅰ和Ⅱ两个涡旋旋向相同,都是顺时针方向,Ⅰ处涡旋恰好阻止上凸台空泡长大,而Ⅱ处涡旋却促进了下凸台空泡长大。两处涡旋的速度相对狭缝处主流来说非常小,主流携带两侧空泡向下游移动,导致在下游靶区范围内汇聚了大量的来自上、下凸台的脱落空泡群,经过融合之后破裂溃灭。此外,结合图9各个区域内壁面剪切力变化曲线可知,区域3的壁面剪切力幅值最大,变化周期最小,区域4～6周期逐渐增大,幅值逐渐变小。这说明空泡群的汇聚溃灭产生较高流速冲击,使区域3内空泡破裂频率和剪切力叠加幅值达到最大,进而对壁面会有较大的损伤,而在下游区域4、5、6受到空泡群破裂溃灭的影响越来越弱,损伤程度逐渐降低。

3 结 论

(1)模拟结果表明,ZGB空化模型对空化室内模拟计算的适用性好,与实验吻合性好。

(2)随着进出口压差增大,空化室下游主流场内湍动加剧,狭缝上下游压力分布梯度增大,区域Ⅰ、Ⅲ的涡旋范围和中心压力值也增大,但中心位置基本不变,而Ⅱ区域涡旋范围却逐渐减小。

(3)空泡的演化过程规律明显,呈现出空化初生、发展、脱落、分离、融合、溃灭的准周期性过程。由于流道结构影响,上、下凸台空化初生依附点位于两凸台圆心连线上,两位置处空泡演化周期有差别,但基本演化规律一致,上凸台的空泡演化周期约为0.057 s,下凸台的约为0.059 s。下凸台下游流场空间范围大,空泡的演化行为也更加显著,而上凸台后缘则基本上一直存在高压涡旋区,且范围较小,会抑制空泡生长和发展。依据液相汽化体积分率可知,下凸台为主要空化依附位置。

(4)空泡演化的周期性导致靶区内壁面剪切力受空化效应的叠加影响同样呈现出周期性变化;空泡群的汇聚和破裂导致不同位置的壁面剪切力变化不同,并影响最终的损伤结果,使得损伤速率沿着流动方向迅速增大,达到峰值之后逐渐减小。